Main

The switching of magnetization between two metastable states is very similar to the process of transferring a particle over a potential barrier from one minimum to another (see Fig. 1). The obvious way for such a transfer is to pull the particle over the barrier and let it relax into the new metastable state. Such a scenario is followed in the switching of ferromagnetic spins over 180∘ by a magnetic-field pulse2,3,4,5,6,7. For optimal switching speed the pulse width has to be tuned to half the precessional period. Nevertheless, it has been recently shown that if the pulse is shorter than 2 ps the required magnetic field is so strong that the magnetic order collapses and the switching becomes a non-deterministic process3.

Figure 1: Non-inertial and inertial models to transport a point mass over a potential.
figure 1

The non-inertial mechanism requires a continuous driving force that pulls the mass over the potential barrier. A similar scenario is realized in magnetization reversal through precessional motion in ferromagnets. In contrast, in the inertial mechanism, during the action of the driving force the coordinate of the particle is hardly changed, but the particle acquires enough momentum to overcome the barrier afterwards.

Full size image

Alternatively, for massive particles such a potential barrier can be overcome by using their inertia. Even if the interaction between an external stimulus and the particle is so short that the coordinate of the particle hardly changes during the interaction time, as long as the particle acquires sufficient linear momentum and kinetic energy it may overcome the potential barrier afterwards. Were such an inertial mechanism of spin switching feasible, we could control magnetization with magnetic-field pulses much shorter than those required for non-inertial switching.

All magnetically ordered materials can be divided into two groups: ferromagnets and antiferromagnets, the static and dynamic magnetic properties of which are fundamentally different8. The dynamics of spins Si in a ferromagnet is described in terms of the magnetization vector M=Σ Si, the motion of which in an effective magnetic field Heff is governed by the Landau–Lifshitz equation dM/dt=γ(M×Heff) (γ is the gyromagnetic ratio)1,8. This equation is of first order with respect to time, t, and thus does not contain inertial terms such as acceleration. In contrast, the dynamics of an antiferromagnet with two sublattices M1 and M2 is described in terms of the motion of the antiferromagnetic unit vector l=(M1−M2)/|M1−M2|, which can be written through the variation of the Lagrangian (refs 9, 10 and Supplementary Information) for l only,

whereas the magnetization M=M1+M2 is only a slave variable. Here W(l) plays the part of the potential energy, He and H represent the exchange field of the antiferromagnet and the external magnetic field, respectively. This Lagrangian includes the kinetic energy, dl/dt (ref. 2), and hence the equation of motion is of second order with respect to time and shows inertial-like motion. This statement is valid even for canted antiferromagnets, where the Dzyaloshinskii–Moriya interaction leads to a non-zero magnetic moment in the ground state. In this case,

where Wa(l) describes the effective anisotropy energy and the vector HD is the Dzyaloshinskii field of the antiferromagnet, determined by the magnetic symmetry 9,10. Therefore, antiferromagnetically coupled spins do have inertia and this property can be exploited for ultrafast magnetic switching using ultrashort magnetic-field pulses.

Holmium orthoferrite HoFeO3 is an excellent candidate for observing such inertial reorientation of spins. (1) It is a canted antiferromagnet with a Dzyaloshinskii field of about 10 T parallel to the y axis, leading to a small magnetic moment in the x z plane. Owing to this net magnetization and the last term in equation (2), an external magnetic field can play the part of a driving force for the vector l and thus trigger an inertial spin motion. (2) Between T1=38 K and T2=58 K the magnetic system of HoFeO3 is characterized by two thermodynamical potential minima11,12,13. One persists up to T2=58 K and corresponds to the Γ12 magnetic symmetry, with the magnetic moment M along the x crystallographic axis and the antiferromagnetic vector l in the z y plane (Fig. 2). In angular variables, lz=cosθ, lx=sinθsinϕ and ly=sinθcosϕ, the Γ12 phase has θ=θ(T)≠0, π/2,… and ϕ=0, π (see Fig. 2). The second potential minimum is present above T1=38 K and corresponds to the Γ24 phase with both M and l in the x z plane θ=θ(T)≠0, π/2,… and ϕ=±π/2. The transition between these two minima is a first-order phase transition at Tt=52 K, where θ(Tt)=θ0 is about 15∘–20∘(refs 11, 12, 13), which can be achieved either by heating or by the application of a static magnetic field.

Figure 2: Spin switching in HoFeO3.
figure 2

Γ12 and Γ24 are the two metastable phases present between 38 and 52 K. H represents an effective magnetic-field pulse that initiates an inertial motion of spins from the Γ12 to the Γ24 magnetic phase. In the Γ12 phase the antiferromagnetic vector l is in the y z plane and the z component of magnetization M is zero. A transition towards the Γ24 phase occurs through a rotation of the l vector over an angle δ ϕ towards the new equilibrium in the z x plane with a non-zero MZ component.

Full size image

From equations (1) and (2) it can be easily shown that in HoFeO3 between 38 and 58 K a short magnetic field pulse should trigger an inertial spin-reorientation between the magnetic phases Γ12 and Γ24. A laser pulse propagating along the z axis acts as an effective magnetic field H=H(t)ez (ref. 16). Supposing θ=const, it follows from equations (1) and (2) that

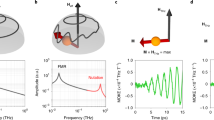
Here, the acceleration d2ϕ/dt2 indeed represents the spin inertia, similar to that in the Newton equation of motion for unit mass; the second term presents a viscous force with damping coefficient Γ; terms with dw(ϕ)/dϕ and HD represent the restoring and driving force, respectively; w(ϕ) is a dimensionless function proportional to the magnetic anisotropy energy for θ=const; ω0 is the frequency of the lower antiferromagnetic mode at T=Tt. We can see that, for the phase Γ12 with ϕ=0 in the ground state, H(t) acts as a force exciting the dynamics of the ‘coordinate’ ϕ, whereas the effect of the field is negligible for the Γ24 phase with ϕ=π/2 in the ground state. Results of calculations on the basis of equation (3) are shown in Fig. 3a. It is seen that the excitation of the spins by a 100 fs magnetic-field pulse with an amplitude HP triggers damped spin oscillations and may change the equilibrium value of the angle ϕ. The new equilibrium orientation depends on the amplitude of the optically induced field pulse: if the pulse amplitude HP<HC, the system relaxes back to the initial state ϕ=0; for HP>HC, the resulting state is the Γ24 phase with ϕ=±π/2. The value of the critical field for HoFeO3 is of the order of 0.5 T. Figure 3 shows that the coordinate ϕ of the spin hardly changes during the 100 fs action of the magnetic field. Instead, the spins acquire sufficient momentum to overcome the potential barrier afterwards. The short magnetic pulse triggers a motion with an essentially constant value dϕ/dt. The motion persists long after the pulse is gone. The speed of overcoming the potential barrier is given by the frequency of the spin-wave resonance in the magnet and for this particular case is equal to 0.5 rad ps−1. This is much faster than the speed of spin switching measured earlier for ferromagnets (∼0.0314 rad ps−1; refs 4, 5, 6, 7).

Figure 3: Theoretical and experimental demonstration of inertia-driven spin switching in HoFeO3.
figure 3

a, In the calculations, the reorientation is assumed to be triggered by a 100-fs Gaussian magnetic-field pulse directed along the z axis. Magnetic parameters are taken from refs 11 and 12. HC is the critical field required for the transition . The simulations show that for T=50.5 K the critical field is equal to 0.6 T. b, In the experiment, the effective magnetic fields along the z axis were generated by right-handed σ(+) and left-handed σ(−) circularly polarized laser pulses through the inverse Faraday effect. The trace recorded at T=53.6 K for left-handed circularly polarized pump σ(−) is shown by green points and demonstrates that outside the range between 38 and 52 K no inertia-driven spin switching is seen. Note that the simulations do not take into account laser-induced heating. The latter is likely the reason for the different oscillation amplitudes observed experimentally for σ(−) and σ(+).

Full size image

To observe this inertial motion of spins in HoFeO3 we carried out pump–probe experiments with 100 fs laser pulses, producing an effective magnetic field by a circularly polarized pump pulse owing to the inverse Faraday effect. The field is proportional to [E(ω)×E*(ω)], where E(ω) is the electric field of the light wave at frequency ω, and present in the medium only during the action of the laser pulse14,15. Rare-earth orthoferrites are known to possess large inverse Faraday effects resulting in effective magnetic fields up to 1 T (ref. 16), directed along the wavevector of light. Right- and left-handed circularly polarized pulses act as fields of opposite orientation. The pump-induced spin dynamics was monitored by detecting the MZ component of the magnetization through the magneto-optical Faraday effect in the probe pulse, measured as a function of delay between the pump and probe pulses. The results of such time-resolved measurements are shown in Fig. 3b for the two opposite pump helicities. The experimental observations are in excellent agreement with the results of the simulations and are an experimental demonstration of an inertial motion of antiferromagnetically coupled spins in HoFeO3, triggered by a short optically generated magnetic-field pulse. Outside the range between T1=38 K and Tt=52 K, such pulses cause only small-amplitude damped oscillations towards the initial state, similar to that observed in ref. 16. This again strongly confirms the original hypothesis that the dynamics shown in Fig. 3 is related to a reorientation from the Γ12 into the Γ24 magnetic phase.

It is interesting to note that although the two magnetic phases coexist between T1=38 K and T2=58 K, in the stroboscopic pump–probe experiment the switching from the Γ12 to the Γ24 phase can be seen only in the range from T1=38 K and Tt=52 K. Below 52 K, the Γ12 phase has lower energy and the switching of the spin system from Γ12 to Γ24 will be followed by thermal relaxation so that the system will be thermodynamically restored into the initial Γ12 state. Above 52 K, Γ24 has a lower energy, and after the spins are switched from Γ12 to Γ24, their initial state is not restored and the switching process cannot be observed in a stroboscopic experiment.

It must be mentioned that the agreement between theory and experiment is observed only within the first few hundred picoseconds after the laser pulse action (see Fig. 4a). Time-resolved measurements of the Faraday rotation at different temperatures and for time delays up to 1.2 ns clearly show that the difference between experiments with opposite pump helicities vanishes beyond 600 ps. To explain such laser-induced magnetic changes for longer delays we should note that owing to absorption (k=300 cm−1) the excitation of the material with the laser pulse leads to a rapid increase of lattice temperature of about 12 K. Such a heating can also result in a spin-reorientation between the phases Γ12 and Γ24. However, in contrast to the effect triggered by a laser-induced effective magnetic field as discussed above, such a reorientation does not depend on the helicity of the optical excitation. To separate the field-driven and heat-driven spin reorientation we should separate the helicity-dependent and helicity-independent contributions to the magneto-optical rotation, respectively. These contributions were calculated as the difference and the sum of the Faraday rotation measured for the two opposite pump helicities. These quantities were normalized on the Faraday rotation at Tt=52 K (0.27∘) and the results are shown in Fig. 4b in terms of laser-induced changes of the magnetization MZ. The figure clearly shows that the spin reorientation triggered by a laser-generated effective magnetic field is two orders of magnitude faster than the similar reorientation triggered by a rapid temperature increase. Moreover, the time constant (of about 200 ps) of the relaxation of the helicity-dependent contribution to ΔMZ remarkably coincides with the time constant of the heat-driven increase of ΔMZ (see Fig. 4b). Such a slow dynamics can be explained as a relaxation of a medium towards thermal equilibrium through the relaxation of unfavourable and growth of favourable Γ24 domains. Note that the temperature dependencies of the efficiency of both heat-induced and field-induced magnetic changes are very typical for non-uniform laser-induced phase transitions17,18 (see Fig. 4c). The fact that ΔMZ//MZ averaged over the probed volume was only about 8% is most probably caused by a non-uniformity of pump intensity over the probed volume. It is important to stress that the absolute value of the Faraday effect in orthoferrites is seriously influenced by linear birefringence. In particular, it has been shown that because of the linear birefringence the amplitude of the laser-induced magnetic changes probed through the Faraday effect in orthoferrites can be easily underestimated19,20.

Figure 4: Laser-induced spin dynamics measured by the Faraday rotation at different temperatures.
figure 4

a, Dynamics of the Faraday rotation triggered by right-handed σ(+) and left-handed σ(−) circularly polarized laser pulses. b, Dynamics of spin reorientation driven by laser heating (open circles) and laser-generated magnetic fields (solid circles). c, Temperature dependencies of the spin reorientation driven by laser heating (solid circles) and laser-generated magnetic fields (open circles).

Full size image

The new mechanism of spin switching based on the inertia of the spin system in antiferromagnets, as demonstrated here, enables us to trigger the writing of one bit of information using extremely short magnetic-field pulses. Such an inertial mechanism of magnetic writing opens new opportunities for sequential writing of a large number of data, for example the realization of three-dimensional displays and many other applications where reaching the ultimate speed of addressing one bit is extremely important, whereas the actual switching of one bit between two states may occur at a much slower timescale. Finally, we would like to note that inertia-driven spin switching is not limited to antiferromagnets. Even if a subpicosecond magnetic pulse alone cannot switch the magnetization of a single ferromagnetic layer3 and the assistance of a strong electric field is required21, in a heterostructure made of two ferromagnetic layers with a strong antiferromagnetic coupling (as in a so-called artificial antiferromagnet used for exchange biasing GMR-type sensors), switching with an ultrashort magnetic pulse is possible through the inertial mechanism.

Methods

Experiment.

To monitor the magnetization dynamics in HoFeO3, the Faraday effect, that is the rotation of the polarization plane of light with wavevector k transmitted through the sample with magnetization M, was measured, αF=χ Mk (χ is the magneto-optical susceptibility)8. In the experiments we used thick 60-μm plates of HoFeO3 cut perpendicularly to the z axis. The time-resolved measurements of the Faraday rotation were made in a pump-and-probe configuration at a photon energy of 1.52 eV using amplified 100-fs pulses from a Ti:sapphire laser at a repetition rate of 1 kHz. The intensity ratio between the pump and probe pulses was about 100. Both beams were focused on the sample to a spot diameter of about 100 μm for the pump and somewhat smaller for the probe beam. The pump fluence on the sample was around 10 mJ cm−2. The experiments were carried out at normal incidence and in a magnetic field of about Happl=100 Oe applied along the z axis. To separate the transient magneto-optical Faraday effect from possible artefacts, we have measured the polarization rotation α or the two polarities of the field and have taken the difference αF=α(+Happl)−α(−Happl).

Theory.

In equation (3), the anisotropy energy is modelled by standard expansion over components of the vector l to fourth order. For a magnetic field pulse of short duration Δt≪1/ω0, equation (3) was solved numerically and analytically, replacing the real pulse shape by a Dirac delta function, H(t)→HpΔt δ(t), . Then before (t<0) and after (t>0) the action of the pulse, the spin dynamics is described by equation (3) with H(t)=0. Assuming ϕ=0 at t<0 it is easy to find the initial conditions of the form ϕ=0, d ϕ/dt=γ2HDHpΔt/sinθ0, which gives the solution of equation (3) in the same form of a damped nonlinear oscillation as in Fig. 3.