Abstract
Topological insulators, with metallic boundary states protected against time-reversal-invariant perturbations1, are a promising avenue for realizing exotic quantum states of matter, including various excitations of collective modes predicted in particle physics, such as Majorana fermions2 and axions3. According to theoretical predictions4, a topological insulating state can emerge from not only a weakly interacting system with strong spin–orbit coupling, but also in insulators driven by strong electron correlations. The Kondo insulator compound SmB6 is an ideal candidate for realizing this exotic state of matter, with hybridization between itinerant conduction electrons and localized f-electrons driving an insulating gap and metallic surface states at low temperatures5. Here we exploit the existence of surface ferromagnetism in SmB6 to investigate the topological nature of metallic surface states by studying magnetotransport properties at very low temperatures. We find evidence of one-dimensional surface transport with a quantized conductance value of e2/h originating from the chiral edge channels of ferromagnetic domain walls, providing strong evidence that topologically non-trivial surface states exist in SmB6.
Similar content being viewed by others
Main
First reported over 40 years ago6, the long-standing puzzle of saturating electrical resistivity in SmB6 at low temperatures6 has recently found a possible solution7,8,9,10,11,12,13,14,15,16. Recent transport experiments7,8,15,16 have proved the existence of metallic conduction at the surface of SmB6 crystals at temperatures much below the opening of the hybridization gap, where surface conductance dominates that of the insulating bulk of the crystal, as shown by nonlocal transport7, sample thickness dependence and surface gating studies17. However, polarity-driven surface states14 and lack of direct evidence of the chiral nature of surface conduction has brought into question the topological nature of these states. In this study, we combine observations of a suppression of weak antilocalization by spin-flip scattering, an anomalous Hall effect (AHE), a hysteretic irreversibility in magnetoresistance (MR) and an unusual enhanced domain wall conduction to prove the occurrence of long-range ferromagnetic (FM) order that gaps the Dirac spectrum of the topological surface states and relegates conduction to chiral edge channels.
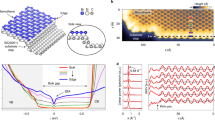
The overall magnetoresistance in SmB6 is negative at low temperatures and varies quadratically with field, which can be attributed to the reduction of the Kondo energy gap by magnetic field and the liberation of bulk charge carriers18. The MR measurements in a perpendicular field orientation (H⊥ ≡ H ‖ [001], I ‖ [100]), obtained while applying an increasing (up-sweep) field, or Hup (Fig. 1a), are qualitatively similar to those taken with a decreasing (down-sweep) field, or Hdn (Fig. 1b), but with notable differences. For instance, below 500 mK an oscillatory behaviour in the MR is visible in the up-sweep data, reminiscent of Shubnikov–de Haas oscillations, whereas it is nearly absent in the down-sweep MR data, as shown in Fig. 1b. Furthermore, on close inspection of the down-sweep MR data, abrupt transition-like features are apparent at low Hdn fields that are completely absent in the up-sweep data. Below 200 mK, the magnetoresistance abruptly drops through transition-like steps at low Hdn fields, as shown in the inset of Fig. 1b. To compare directly, Fig. 2a presents MR data at 100 mK obtained by systematically sweeping through the full ‘four-quadrant’ range, revealing a stark contrast between up- and down-sweep MR. This takes the form of a hysteretic loop that does not depend on the sign of the field, but only on the sweep direction. The hysteretic loop seems to close at a field of 8–10 T, with no difference in Hup or Hdn MR above that range, and vanishes if the turning field is less than 4 T (see Supplementary Methods).
a, Four-wire measurements on a slab-shaped polished sample (see Supplementary Methods) were measured in a perpendicular magnetic field orientation (H ‖ [001], I ‖ [100]) on increasing magnetic field, taken at constant temperatures between 20 mK and 1 K, where surface conduction dominates that of the bulk material. The temperature dependence of resistivity in zero field is shown in the inset, normalized to its room-temperature value. b, Magnetoresistance taken in the same perpendicular field orientation but measured on down-sweep of field, showing qualitatively similar behaviour as for up-sweep data, but with notable differences, including a strong suppression of the oscillatory amplitude present in up-sweep data, as well as abrupt transition-like jumps in the data as highlighted in the inset zoom (solid lines are guides to the eye). These differences are ascribed to the presence of ferromagnetism, as described in the text.
a, Full ‘four-quadrant’ magnetoresistance hysteresis loop of SmB6 in perpendicular magnetic field orientation (I ‖ [100], H ‖ [001]) measured at 100 mK. We observe a butterfly shape hysteresis that is sign-reversed from that of conventional ferromagnetic materials, and is interrupted before zero field is crossed by a discontinuous jump at low field that does not depend on field sign, as highlighted by the inset zoom. b, Anomalous Hall effect in the low-temperature Hall resistance. A prominent kink is present in low-temperature (100 mK) data near a field of 8 T, where the hysteresis loop closes, indicating the presence of ferromagnetic order. The kink is absent at higher temperatures (1 K), where the hysteresis in magnetoresistance also vanishes. c, Field dependence of the difference of Hall resistance ΔRyx = Ryx − AH, where A is a linear coefficient obtained from a fitting below 5 T at 100 mK. An onset associated with the anomalous Hall effect is easily discernible at 8 T.
Field-dependent hysteretic phenomena can have different origins, but are typically associated with the presence of ferromagnetism. As no bulk magnetic order is observed in SmB6 according to muon spin resonance experiments performed down to 20 mK (ref. 19), a surface-based FM order is the likely explanation, as discussed in detail below. Its hallmark signature, the anomalous Hall effect20, is one direct way to confirm its presence. As shown in Fig. 2b, the Hall resistance of SmB6 at 1 K is completely linear and negative, consistent with previous reports17,21,22. However, at 100 mK a kink is clearly discernible in the raw data precisely near 8 T, the field at which the hysteretic loop in MR closes. Plotted with a linear background subtracted, the difference ΔRyx = Ryx − AH (where A is a linear coefficient obtained from fitting Ryx below 5 T) exhibits an abrupt onset, yet lack of hysteretic behaviour (see Supplementary Methods), as seen in Fig. 2c, suggesting that the observed Hall resistance has an AHE term RyxA associated with FM domain alignment. Together with the observation of a field-history-dependent dynamics, as indicated by the presence of a strongly asymmetric time relaxation in MR between Hup and Hdn (see Supplementary Methods), these observations confirm without a doubt the presence of FM domains.
Shown in Fig. 3a, b, the MR hysteresis also depends on the magnetic field orientation with respect to the sample. When the field is oriented parallel to the surface with electrical contacts (H‖ ≡ H ‖ [010], I ‖ [100]), the difference in up- and down-sweep MR becomes vanishingly small in magnitude. As it is very unlikely that a bulk-origin anomaly would break the cubic symmetry of the crystal, it is clear that this anomalous MR hysteresis stems from a surface-based origin.
a, Comparison of magnetoresistance measured at 100 mK on sweeping magnetic field up and down (see arrows) with the field orientation perpendicular to the large surface of the sample with contacts. A hysteretic loop is evident between a closing field of ∼10 T and a discontinuous jump at low field. b, The hysteresis is greatly suppressed when field is oriented parallel to the measurement plane, as shown for the same sample as in a (with contacts reapplied). c, Weak antilocalization is also observed at low fields and temperatures, but with a surprisingly small coefficient of α = 0.17 (see text) for the perpendicular field orientation. d, When the field is applied parallel to the measurement plane, the weak antilocalization correction is much larger with α = 0.29 (see text), indicating a very strong anisotropy opposite to that expected for the usual orbital configuration originating from the finite penetration depth λ, but consistent with strong spin-flip scattering. Solid lines are fits to the data using the WAL correction formula (see text).
The observation of weak antilocalization (WAL) confirms this picture. In two-dimensional conductors, weak localization appears as a quantum correction to classical magnetoresistance caused by the constructive or destructive interference between time-reversed quasiparticle paths. The presence of strong spin–orbit coupling or a π Berry’s phase associated with the helical states of a topological insulator (TI)23 changes the sign of the correction and gives rise to the signature WAL enhancement of conductance, which is suppressed by a time-reversal-symmetry-breaking perturbation.
As shown in Fig. 3c, d, we observe signatures of WAL at low fields in both field orientations, with a strong anisotropy evident. Because the WAL effect is normally sensitive only to the perpendicular field component, as it is an orbital effect, it is surprising to see any WAL correction in the H‖ field orientation at all, as shown in Fig. 3d. However, one must consider the finite width of the surface conducting state wavefunction that penetrates into the bulk with a characteristic length λ, which combined with the rather small insulating gap of SmB6 leads to a situation where orbital motion of electrons can occur even in the H‖ field orientation.
Using the appropriate version of the Hikami–Larkin–Nagaoka (HLN) equation (see Supplementary Methods), we fit the 20 mK low-field sheet conductance for each field orientation, as shown in Fig. 3c, d, extracting the dephasing length Lφ and the conduction channel α parameter for each. Whereas Lφ in each field orientation is comparable to previous results16, the value α⊥ = 0.17 is much smaller than the α = 2 × 1/2 = 1 value expected in the presence of top and bottom surface conduction channels (per Dirac cone)16. Surprisingly, the parallel field orientation fit yields α‖ = 0.29, which is small but still much larger than α⊥. We attribute the overall strong suppression (α < 1) and the unusual anisotropy (α‖ > α⊥) of these values to the presence of spin-flip scattering, which is known to reduce the WAL effect as a result of destructive interference, leading to α = 0 in the extreme limit where spin-flip scattering is much stronger than spin–orbit scattering24,25.
Together with MR hysteresis, the presence of spin-flip scattering suggests the existence of magnetic moments on the surface of SmB6. These are probably associated with samarium ions, either via the presence of unscreened f-electron Sm moments (so-called ‘Kondo holes’26) proposed to explain logarithmic corrections to surface conductance at low temperatures16, or possibly Sm3+ moments in a native surface oxide layer observed by X-ray photoelectron spectroscopy27. With ample charge carriers present on the surface of SmB6, these moments can play a similar role to that of magnetic impurities on the surface of a TI system in stabilizing ferromagnetism28: in the presence of conducting Dirac electron surface states, magnetic order can be stabilized via Ruderman–Kittel–Kasuya–Yosida (RKKY) interactions, and is guaranteed to be of the FM type if the chemical potential is close to the Dirac point owing to a small Fermi wavenumber28.
We define a Curie temperature of TC ≃ 600 mK by the onset of magnetotransport hysteresis, as shown in Fig. 4a. The associated hysteretic MR loop is, however, quite different from the conventional butterfly shape commonly observed in FM materials. First, it is not centred around zero magnetic field, but rather closes abruptly before zero field is reached on down-sweep. The type of magnetization leading to such hysteresis is not consistent with the usual overshoot that is necessary to overcome a coercive field, but does indeed occur in certain situations (see Supplementary Methods). Second, the increased scattering observed in SmB6 on decreasing field (that is, R(Hdn) > R(Hup)) is opposite to that usually observed in a ferromagnet, where scattering associated with domain walls is typically enhanced on magnetization reversal. Rather, there is an enhanced conductance in SmB6 on up-sweep that is diminished on reaching the closing field and returning to low fields. Interestingly, equivalent behaviour was observed in Mn-doped Bi2(Te, Se)3 thin films tuned by ionic liquid gating techniques29. In this ferromagnetic TI system, a reversal of the usual butterfly shape occurs on gating the system into the bulk gap regime, where the TI chiral conducting modes trapped by domain walls result in an anomalous Hall conductance associated with a quantum Hall droplet1. In this picture, the domain wall conductance is enhanced during reversal of the magnetization because the number of domain walls increases; at the coercive field, where the number of the domain walls is a maximum, the conductance exhibits a maximum. In SmB6, similar behaviour is readily shown by plotting the difference in conductance, ΔG = Gup–Gdn (see Fig. 4b), where Gup (Gdn) is the magnetoconductance for Hup (Hdn). With decreasing temperature, ΔG is gradually enhanced and the peak position shifts to higher field. The temperature dependence of this characteristic field H∗ follows a mean-field-like order parameter dependence that terminates at the Curie temperature TC = 600 mK, as shown in the inset of Fig. 4b. We therefore interpret H∗ as a coercive field, in terms of the enhancement of the conductance due to a maximum number of minority domains.
a, Magnetoconductance G of SmB6 for perpendicular field orientation (20 mK and 100 mK data are vertically offset by −1.2e2/h and −0.3e2/h, respectively, for clarity). The closure of the hysteretic loop with increasing temperature is consistent with the loss of surface ferromagnetism at a Curie temperature of ∼600 mK. The enhanced (decreased) conductance on up(down)-sweep is opposite to that expected in conventional ferromagnetic metals, providing an indication of the topological nature of the surface conducting states (see text). b, Magnetic field dependence of the difference of up- and down-sweep magnetoconductance ΔG = Gup–Gdn. The appearance of one quantum of conductance e2/h in the low-temperature limit provides evidence for a scenario where surface ferromagnetism gaps the topological conducting states within magnetic domains on the surface, limiting conductance to the domain walls. Arrows indicate the characteristic field H∗ where a maximum in ΔG is associated with a coercive field (see text). The inset presents the evolution of H∗, consistent with the onset of ferromagnetic order at 600 mK. c, Schematic representation of the proposed grid-like ferromagnetic domain structure with walls separating domains of oppositely oriented moments, forming a virtual random resistor network with quantized conductance components G1 = e2/h in the presence of dissipation. The conductance between any two non-adjacent nodes in such a network is of the order of G1. d, Schematic band structure for SmB6 at the Γ and X/Y high-symmetry points. Owing to the localized ordered moments, energy gaps are induced at the Dirac points, meaning the Dirac bands become massive. Because the chemical potential μ is fixed at one value, it probably falls within the gap of one band but not in the other (see text).
Below 100 mK, the peak conductance at H∗ reaches a value of ∼e2/h, a value observed in several samples with a wide range of residual sheet resistance values and sample dimensions (see Supplementary Methods), indicating that the observed conductance of e2/h is not coincidental and possibly quantized. We suggest that the quantized conductance signature originates from transport of massive Dirac carriers along one-dimensional channels that lie between FM domains. In this scenario, the domain wall conductance is equal to the anomalous quantum Hall conductance, quantized as (n + 1/2)e2/h, as expected in a massive Dirac spectrum induced by FM ordered moments pointing out of the surface plane1,30.
In an ideal system with no dissipation, ballistic transport should occur and exactly quantized conductance should be observed, as is the case for refs 31,32. However, in non-ideal systems the chiral surface states suffer from abundant inelastic scattering due to electron correlations33 or the ‘puddling’ effect of spatial variations in the electronic structure34, both of which easily suppress ballistic quantum transport and lead to deviations from an exactly quantized conductance. The peculiar temperature- and field-dependent nature of the domain wall conductance, as well as the strong sample variation (see Supplementary Methods), provide a picture quite consistent with this situation.
Furthermore, the presence of a grid-like FM domain structure introduces another degree of complexity in the presence of dissipation. Provided the characteristic FM domain size is sufficiently smaller than the approximately mm-scale sample dimension, the domain walls will effectively form an infinite resistor (conductor) network with R1 = h/e2(G1 = e2/h) elements, as shown in Fig. 4c. The dissipation or puddling is equivalent to virtual removal of resistors at random from the network, yielding the formation of a random network which consists of a conductance G1 = e2/h distributed randomly with a probability of p and a conductance G2 = 0 distributed randomly with a probability of 1 − p. In such a random network, the percolating conduction gives the equivalent conductance between any two non-adjacent nodes of (2p − 1)G1 (ref. 35), namely, of the order of, but not exactly G1. This naturally explains not only the non-exact e2/h quantization at the coercive field, but also the further deviation from this value on further diminishment from maximum minority domain count with field.
The singular domain wall conductance element G1 of the chiral modes is determined by the chemical potential of the Dirac electrons because multiple quantized channels with (n + 1/2)e2/h could contribute to the conduction in SmB6. A half-quantized conductance of (1/2)e2/h would be expected if the surface state Fermi energy is in the gap and in the lowest Landau level of n = 0. Assuming both top and bottom surfaces contribute equally to the total conductance, this gives the observed value of e2/h = 2 × (1/2)e2/h. Note that three Dirac bands are calculated to reside at the Γ and X/Y points in SmB6(refs 10,11,12,13). The quantized conductance of e2/h suggest that the chemical potential sits in the gap only at the Γ points, whereas it is above the gaps at the X/Y points, as shown in Fig. 4d. In fact, the saturation of sample resistance indicates that there remains surface conduction channels at very low temperatures, as shown in the inset of Fig. 1a. In this case, a quantized anomalous Hall effect in the Hall resistance, such as observed in gate-tuned Cr-doped Bi2Se3 (ref. 31) and BiSbTeSe2 (ref. 32), is probably masked by the conduction of Dirac electrons at the X/Y points. Finally, we note that the abrupt, sharp transitions observed in MR on down-sweep (Fig. 1b inset) often exhibit a jump in conductance very close to (1/2)e2/h; whether this indicates a true quantization, or a unique signature of a chiral domain wall reconfiguration, remains a provocative observation to be explained. With a truly insulating bulk band structure, future gating experiments17 utilizing single-crystal surfaces of SmB6 should readily facilitate the observation of these and other quantized properties in this system.
References
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Wilczek, F. Majorana returns. Nature Phys. 5, 614–618 (2009).
Wilczek, F. Two applications of axion electrodynamics. Phys. Rev. Lett. 58, 1799–1802 (1987).
Dzero, M., Sun, K., Galitski, V. & Coleman, P. Topological Kondo insulators. Phys. Rev. Lett. 104, 106408 (2010).
Takimoto, T. SmB6: A promising candidate for a topological insulator. J. Phys. Soc. Jpn 80, 123710 (2011).
Menth, A., Buehler, E. & Geballe, T. H. Magnetic and semiconducting properties of SmB6 . Phys. Rev. Lett. 22, 295–297 (1969).
Wolgast, S. et al. Low-temperature surface conduction in the Kondo insulator SmB6 . Phys. Rev. B 88, 180405 (2013).
Kim, D. J. et al. Surface Hall effect and nonlocal transport in SmB6: Evidence for surface conduction. Sci. Rep. 3, 3150 (2013).
Zhang, X. et al. Hybridization, inter-ion correlation, and surface states in the Kondo insulator SmB6 . Phys. Rev. X 3, 011011 (2013).
Xu, N. et al. Surface and bulk electronic structure of the strongly correlated system SmB6 and implications for a topological Kondo insulator. Phys. Rev. B 88, 121102 (2013).
Neupane, M. et al. Surface electronic structure of the topological Kondo-insulator candidate correlated electron system SmB6 . Nature Commun. 4, 2991 (2013).
Jiang, J. et al. Observation of possible topological in-gap surface states in the Kondo insulator SmB6 by photoemission. Nature Commun. 4, 3010 (2013).
Frantzeskakis, E. et al. Kondo hybridization and the origin of metallic states at the (001) surface of SmB6 . Phys. Rev. X 3, 041024 (2013).
Zhu, Z.-H. et al. Polarity-driven surface metallicity in SmB6 . Phys. Rev. Lett. 111, 216402 (2013).
Kim, D. J., Xia, J. & Fisk, Z. Topological surface state in the Kondo insulator samarium hexaboride. Nature Mater. 13, 466–470 (2014).
Thomas, S. et al. Weak antilocalization and linear magnetoresistance in the surface state of SmB6. Preprint at http://arXiv.org/abs/1307.4133 (2013).
Syers, P., Kim, D., Fuhrer, M. S. & Paglione, J. Tuning bulk and surface conduction in the proposed topological Kondo insulator SmB6 . Phys. Rev. Lett. 114, 096601 (2015).
Cooley, J. C. et al. High magnetic fields and the correlation gap in SmB6 . Phys. Rev. B 52, 7322–7327 (1995).
Biswas, P. K. et al. Low-temperature magnetic fluctuations in the Kondo insulator SmB6 . Phys. Rev. B 89, 161107 (2014).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Allen, J. W., Batlogg, B. & Wachter, P. Large low-temperature Hall effect and resistivity in mixed-valent SmB6 . Phys. Rev. B 20, 4807–4813 (1979).
Cooley, J. C., Aronson, M. C., Fisk, Z. & Canfield, P. C. SmB6: Kondo insulator or exotic metal? Phys. Rev. Lett. 74, 1629–1632 (1995).
Fu, L. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Hikami, S., Larkin, A. I. & Nagaoka, Y. Spin–orbit interaction and magnetoresistance in the two dimensional random system. Prog. Theor. Phys. 63, 707–710 (1980).
Lu, H.-Z. & Shen, S.-Q. Weak localization of bulk channels in topological insulator thin films. Phys. Rev. B 84, 125138 (2011).
Hamidian, M. H. et al. How Kondo-holes create intense nanoscale heavy-fermion hybridization disorder. Proc. Natl Acad. Sci. USA 108, 18233–18237 (2011).
Phelan, W. A. et al. Correlation between bulk thermodynamic measurements and the low-temperature-resistance plateau in SmB6 . Phys. Rev. X 4, 031012 (2014).
Liu, Q., Liu, C.-X., Xu, C., Qi, X.-L. & Zhang, S.-C. Magnetic impurities on the surface of a topological insulator. Phys. Rev. Lett. 102, 156603 (2009).
Checkelsky, J. G., Ye, J., Onose, Y., Iwasa, Y. & Tokura, Y. Dirac-fermion-mediated ferromagnetism in a topological insulator. Nature Phys. 8, 729–733 (2012).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Xu, Y. et al. Observation of topological surface state quantum Hall effect in an intrinsic three-dimensional topological insulator. Nature Phys. 10, 956–963 (2014).
Konig, M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007).
Martin, J. et al. Observation of electron-hole puddles in graphene using a scanning single-electron transistor. Nature Phys. 4, 144–148 (2008).
Kirkpatrick, S. Percolation and conduction. Rev. Mod. Phys. 45, 574–588 (1973).
Acknowledgements
The authors would like to acknowledge I. Appelbaum, J. Cummings, L. Fu, L. Li, T. Pereg-Barnea, J. Sau and I. Takeuchi for extremely valuable discussions. This research was supported by AFOSR (FA9550-14-1-0332) and NSF (DMR-0952716).
Author information
Authors and Affiliations
Contributions
Y.N. and R.W. performed the transport measurements and analysed the data. X.W. and P.S. grew and characterized single crystals of SmB6. J.P. and Y.N. conceived and designed the experiments, and all authors contributed to the editing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 5591 kb)
Rights and permissions
About this article
Cite this article
Nakajima, Y., Syers, P., Wang, X. et al. One-dimensional edge state transport in a topological Kondo insulator. Nature Phys 12, 213–217 (2016). https://doi.org/10.1038/nphys3555
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3555
This article is cited by
-
RETRACTED ARTICLE: Multi-dimensional image edge localization method based on edge symmetry algorithm
Multimedia Tools and Applications (2023)
-
Surface-state plasmons in topological Kondo insulator
Pramana (2022)
-
Emergent long-range magnetic order in ultrathin (111)-oriented LaNiO3 films
npj Quantum Materials (2021)
-
Imaging emergent heavy Dirac fermions of a topological Kondo insulator
Nature Physics (2020)
-
Emergent mystery in the Kondo insulator samarium hexaboride
Nature Reviews Physics (2020)