Abstract
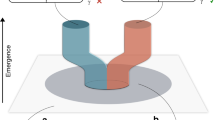
A breaking of symmetry involves an abrupt change in the set of microstates a system can explore. This change has unavoidable thermodynamic implications: a shrinkage of the microstate set results in an entropy decrease, which eventually needs to be compensated by heat dissipation and hence requires work. On the other hand, in a spontaneous symmetry breaking, the available phase-space volume changes without the need for work, yielding an apparent entropy decrease. Here we show that this entropy decrease is a key ingredient of a Szilard engine and Landauer’s principle, and perform a direct measurement of the entropy change along symmetry-breaking transitions for a Brownian particle subject to a bistable potential realized through two optical traps. The experiment confirms theoretical results based on fluctuation theorems, enables the construction of a Szilard engine extracting energy from a single thermal bath, and shows that a signature of a symmetry breaking in a system’s energetics is observable.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Leff, H. S. & Rex, A. F. Maxwell’s Demon. Entropy, Information, Computing (Adam Hilger, 1990).
Parrondo, J. M. R. The Szilard engine revisited: Entropy, macroscopic randomness, and symmetry breaking phase transitions. Chaos 11, 725–733 (2001).
Marathe, R. & Parrondo, J. M. R. Cooling classical particles with a microcanonical Szilard engine. Phys. Rev. Lett. 104, 245704 (2010).
Toyabe, S., Sagawa, T., Ueda, M., Muneyuki, E. & Sano, M. Experimental demonstration of information-to-energy conversion and validation of the generalized Jarzynski equality. Nature Phys. 6, 988–992 (2010).
Bérut, A. et al. Experimental verification of Landauer’s principle linking information and thermodynamics. Nature 483, 187–189 (2012).
Maragakis, P., Spichty, M. & Karplus, M. A differential fluctuation theorem. J. Phys. Chem. B 112, 6168–6174 (2008).
Junier, I., Mossa, A., Manosas, M. & Ritort, F. Recovery of free energy branches in single molecule experiments. Phys. Rev. Lett. 102, 070602 (2009).
Alemany, A., Mossa, A., Junier, I. & Ritort, F. Experimental free-energy measurements of kinetic molecular states using fluctuation theorems. Nature Phys. 8, 688–694 (2012).
Horowitz, J. M. & Parrondo, J. M. R. Optimizing non-ergodic feedback engines. Acta. Phys. Pol. B 44, 803–814 (2013).
Sagawa, T. & Ueda, M. Minimal energy cost for thermodynamic information processing: Measurement and information erasure. Phys. Rev. Lett. 102, 250602 (2009).
Horowitz, J. M., Sagawa, T. & Parrondo, J. M. R. Imitating chemical motors with optimal information motors. Phys. Rev. Lett. 111, 010602 (2013).
Esposito, M. & Van den Broeck, C. Second law and Landauer principle far from equilibrium. Europhys. Lett. 95, 40004 (2011).
Horowitz, J. M. & Vaikuntanathan, S. Nonequilibrium detailed fluctuation theorem for repeated discrete feedback. Phys. Rev. E 82, 061120 (2010).
Horowitz, J. M. & Parrondo, J. M. R. Designing optimal discrete-feedback thermodynamic engines. New J. Phys. 13, 123019 (2011).
Kawai, R., Parrondo, J. M. R. & den Broeck, C. V. Dissipation: The phase-space perspective. Phys. Rev. Lett. 98, 080602 (2007).
Dunkel, J. & Hilbert, S. Phase transitions in small systems: Microcanonical vs. canonical ensembles. Physica A 370, 390–406 (2006).
Vaikuntanathan, S. & Jarzynski, C. Modeling Maxwell’s demon with a microcanonical Szilard engine. Phys. Rev. E 83, 061120 (2011).
Martinez, I. A., Roldán, E., Parrondo, J. M. R. & Petrov, D. Effective heating to several thousand kelvin of an optically trapped sphere in a liquid. Phys. Rev. E 87, 032159 (2013).
Hänggi, P., Talkner, P. & Borkovec, M. Reaction-rate theory: fifty years after Kramers. Rev. Mod. Phys. 62, 251–342 (1990).
Sekimoto, K. Langevin equation and thermodynamics. Prog. Theor. Phys. Suppl. 130, 17–27 (1998).
Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 75, 126001 (2012).
Mandal, D. & Jarzynski, C. Work and information processing in a solvable model of Maxwell’s demon. Proc. Natl Acad. Sci. USA 109, 11641–11645 (2012).
Blickle, V. & Bechinger, C. Realization of a micrometre-sized stochastic heat engine. Nature Phys. 8, 143–146 (2011).
Acknowledgements
I.A.M. and D.P. acknowledge financial support from the Fundació Privada Cellex Barcelona, Generalitat de Catalunya grant 2009-SGR-159, and from the Spanish Ministry of Science and Innovation (MICINN FIS2008-00114, FIS2011-24409). E.R. and J.M.R.P. acknowledge fruitful discussions with S. Grill, M. Jahnel, M. Behrndt, J. M. Horowitz and L. Dinís, and financial support from grants ENFASIS (Spanish Government) and MODELICO (Comunidad de Madrid). This article is dedicated to the memory of D. Petrov, leader of the Optical Tweezers group at ICFO, who passed away on 3 February 2014.
Author information
Authors and Affiliations
Contributions
E.R. analysed experimental data, supported theoretical aspects and the design of the experiment, and performed computer simulations. I.A.M. designed the experiment, and obtained all experimental data. J.M.R.P. proposed and established the project, and developed its theoretical aspects. D.P. designed and supervised the experiment. All authors wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 1045 kb)
Rights and permissions
About this article
Cite this article
Roldán, É., Martínez, I., Parrondo, J. et al. Universal features in the energetics of symmetry breaking. Nature Phys 10, 457–461 (2014). https://doi.org/10.1038/nphys2940
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys2940
This article is cited by
-
One-particle engine with a porous piston
Scientific Reports (2022)
-
Circuit-level convergence of electronics and photonics: basic concepts and recent advances
Frontiers of Optoelectronics (2022)
-
Spontaneous Fluctuation-Symmetry Breaking and the Landauer Principle
Journal of Statistical Physics (2022)
-
Thermodynamics of continuous non-Markovian feedback control
Nature Communications (2020)
-
Large work extraction and the Landauer limit in a continuous Maxwell demon
Nature Physics (2019)