Abstract
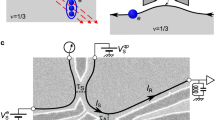
The two-dimensional electron system is a powerful laboratory for investigating the physics of interacting particles. Application of a large magnetic field produces massively degenerate quantum levels known as Landau levels; within a Landau level the kinetic energy of the electrons is suppressed, and electron–electron interactions set the only energy scale1. Coulomb interactions break the degeneracy of the Landau levels and can cause the electrons to order into complex ground states. Here we observe, in the high energy single particle spectrum of this system, salient and unexpected structure that extends across a wide range of Landau level filling fractions. The structure appears only when the two-dimensional electron system is cooled to very low temperatures, indicating that it arises from delicate ground state correlations. We characterize this structure by its evolution with changing electron density and applied magnetic field, and present two possible models for understanding these observations. Some of the energies of the features agree qualitatively with what might be expected for composite fermions, which have proven effective for interpreting other experiments in this regime. At the same time, a simple model with electrons localized on ordered lattice sites also generates structure similar to that observed in the experiment. Neither of these models alone is sufficient to explain the observations across the entire range of densities measured. The discovery of this unexpected prominent structure in the single particle spectrum of an otherwise thoroughly studied system suggests that there exist core features of the two-dimensional electron system that have yet to be understood.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout

 energy dependence indicates that the sashes originate with electron–electron interactions within the lowest Landau levels.
energy dependence indicates that the sashes originate with electron–electron interactions within the lowest Landau levels.



Similar content being viewed by others
References
Jain, J. K. Composite Fermions (Cambridge Univ. Press, 2007)
Dial, O. E., Ashoori, R. C., Pfeiffer, L. N. & West, K. W. High-resolution spectroscopy of two-dimensional electron systems. Nature 448, 176–179 (2007)
Chan, H. B., Glicofridis, P. I., Ashoori, R. C. & Melloch, M. R. Universal linear density of states for tunneling into the two-dimensional electron gas in a magnetic field. Phys. Rev. Lett. 79, 2867–2870 (1997)
Luhman, D. R., Tsui, D. C., Pfeiffer, L. N. & West, K. W. Electronic transport studies of a systematic series of GaAs/AlGaAs quantum wells. Appl. Phys. Lett. 91, 072104 (2007)
Ashoori, R. C., Lebens, J. A., Bigelow, N. P. & Silsbee, R. H. Equilibrium tunneling from the 2-dimensional electron-gas in GaAs — evidence for a magnetic-field-induced energy-gap. Phys. Rev. Lett. 64, 681–684 (1990)
Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Coulomb barrier to tunneling between parallel two-dimensional electron systems. Phys. Rev. Lett. 69, 3804–3807 (1992)
Ashoori, R. C., Lebens, J. A., Bigelow, N. P. & Silsbee, R. H. Energy gaps of the two-dimensional electron gas explored with equilibrium tunneling spectroscopy. Phys. Rev. B 48, 4616–4628 (1993)
Yang, S.-R. E. & Macdonald, A. H. Coulomb gaps in a strong magnetic field. Phys. Rev. Lett. 70, 4110–4113 (1993)
Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Compressibility of the two-dimensional electron gas: measurements of the zero-field exchange energy and fractional quantum Hall gap. Phys. Rev. B 50, 1760–1778 (1994)
Khrapai, V. S. et al. Direct measurements of fractional quantum Hall effect gaps. Phys. Rev. Lett. 99, 086802 (2007)
Sondhi, S. L., Karlhede, A., Kivelson, S. A. & Rezayi, E. H. Skyrmions and the crossover from integer to fractional quantum Hall effect at small Zeeman energies. Phys. Rev. B 47, 16419–16426 (1993)
Barret, S. E., Dabbagh, G., Pfeiffer, L. N., West, K. W. & Tycko, R. Optically pumped NMR evidence for finite-size skyrmions in GaAs quantum wells near Landau level filling ν = 1. Phys. Rev. Lett. 74, 5112–5115 (1995)
Schmeller, A., Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Evidence for skyrmions and single spin flips in the integer quantized Hall effect. Phys. Rev. Lett. 75, 4290–4293 (1995)
Gallais, Y., Yan, J., Pinczuk, A., Pfeiffer, L. N. & West, K. W. Soft spin wave near ν = 1: evidence for a magnetic instability in skyrmion systems. Phys. Rev. Lett. 100, 086806 (2008)
Halperin, B. I., Lee, P. A. & Read, N. Theory of the half-filled Landau level. Phys. Rev. B 47, 7312–7343 (1993)
Hirjibehedin, C. F., Pinczuk, A., Dennis, B. S., Pfeiffer, L. N. & West, K. W. Crossover and coexistence of quasiparticle excitations in the fractional quantum Hall regime at ν≤1/3. Phys. Rev. Lett. 91, 186802 (2003)
Peterson, M. R. & Jain, J. K. Flavor altering excitations of composite fermions. Phys. Rev. Lett. 93, 046402 (2004)
Morf, R. & d'Ambrumenil, N. Stability and effective masses of composite fermions in the first and second Landau level. Phys. Rev. Lett. 74, 5116–5119 (1995)
Park, K., Meskini, N. & Jain, J. K. Activation gaps for the fractional quantum Hall effect: realistic treatment of transverse thickness. J. Phys. Condens. Matter 11, 7283–7299 (1999)
Leadley, D. R., van der Burgt, M., Nicholas, R. J., Foxon, C. T. & Harris, J. J. Pulsed-magnetic-field measurements of the composite-fermion effective mass. Phys. Rev. B 53, 2057–2063 (1996)
Jain, J. K. Composite-fermion approach for the fractional quantum Hall effect. Phys. Rev. Lett. 63, 199–202 (1989)
Fogler, M. M., Koulakov, A. A. & Shklovskii, B. I. Ground state of a two-dimensional electron liquid in a weak magnetic field. Phys. Rev. B 54, 1853–1871 (1996)
Ando, T. & Uemura, Y. Theory of oscillatory g factor in a MOS inversion layer under strong magnetic fields. J. Phys. Soc. Jpn 37, 1044–1052 (1974)
Pikus, F. G. & Efros, A. L. Coulomb gap in a two-dimensional electron gas with a close metallic electrode. Phys. Rev. B 51, 16871–16877 (1995)
Acknowledgements
We are grateful to A. MacDonald and Y. Meir, who independently suggested the identification of sash features with nearby localized states that formed the basis for the lattice model. We thank P. Lee, L. Levitov and B. Halperin for discussions regarding the interpretation of our results. This work was sponsored by the Office of Science of the US Department of Energy.
Author Contributions O.E.D. built the apparatus and performed measurements and analysis. R.C.A. supervised the work and performed analysis. O.E.D. and R.C.A. prepared the manuscript. L.N.P. and K.W.W. performed the crystal growth.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains Supplementary Figures 1- 6 with legends, Supplementary Material 1-5 and Supplementary References. (PDF 806 kb)
Supplementary Movie 1
This brief video shows the typical results from annealing the electron locations in the semi-classical model. Each frame shows the approximate ground state at a single density in a manner similar to that of supplemental figure 5d; the grey hexagons are empty lattice sites, shown using their Wigner-Seitz cells. Red sites are singly occupied, while yellow sites are doubly occupied. The solution is periodic with a 20 site period in each lattice direction. A single period is highlighted for clarity, and repeated in darker colours to demonstrate how the boundary conditions are met. For this calculation, the disorder was 0.2% of the Coulomb energy, and the setback was 2 magnetic lengths. (MOV 4629 kb)
Rights and permissions
About this article
Cite this article
Dial, O., Ashoori, R., Pfeiffer, L. et al. Anomalous structure in the single particle spectrum of the fractional quantum Hall effect. Nature 464, 566–570 (2010). https://doi.org/10.1038/nature08941
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature08941
This article is cited by
-
Electric field-tuneable crossing of hole Zeeman splitting and orbital gaps in compressively strained germanium semiconductor on silicon
Communications Materials (2023)
-
A good tip
Nature Physics (2023)
-
Time, momentum, and energy resolved pump-probe tunneling spectroscopy of two-dimensional electron systems
Nature Communications (2023)
-
Broken symmetries and excitation spectra of interacting electrons in partially filled Landau levels
Nature Physics (2023)
-
Evolution of the quantum Hall bulk spectrum into chiral edge states
Nature Communications (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.