Abstract
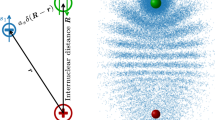
Rydberg atoms have an electron in a state with a very high principal quantum number, and as a result can exhibit unusually long-range interactions. One example is the bonding of two such atoms by multipole forces to form Rydberg–Rydberg molecules with very large internuclear distances1,2,3. Notably, bonding interactions can also arise from the low-energy scattering of a Rydberg electron with negative scattering length from a ground-state atom4,5. In this case, the scattering-induced attractive interaction binds the ground-state atom to the Rydberg atom at a well-localized position within the Rydberg electron wavefunction and thereby yields giant molecules that can have internuclear separations of several thousand Bohr radii6,7,8. Here we report the spectroscopic characterization of such exotic molecular states formed by rubidium Rydberg atoms that are in the spherically symmetric s state and have principal quantum numbers, n, between 34 and 40. We find that the spectra of the vibrational ground state and of the first excited state of the Rydberg molecule, the rubidium dimer Rb(5s)–Rb(ns), agree well with simple model predictions. The data allow us to extract the s-wave scattering length for scattering between the Rydberg electron and the ground-state atom, Rb(5s), in the low-energy regime (kinetic energy, <100 meV), and to determine the lifetimes and the polarizabilities of the Rydberg molecules. Given our successful characterization of s-wave bound Rydberg states, we anticipate that p-wave bound states9, trimer states10 and bound states involving a Rydberg electron with large angular momentum—so-called trilobite molecules5—will also be realized and directly probed in the near future.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Boisseau, C., Simbotin, I. & Côté, R. Macrodimers: ultralong range Rydberg molecules. Phys. Rev. Lett. 88, 133004 (2002)
Farooqi, S. M. et al. Long-range molecular resonances in a cold Rydberg gas. Phys. Rev. Lett. 91, 183002 (2003)
Overstreet, K. R., Schwettmann, A., Tallant, J. & Shaffer, J. P. Photoinitiated collisions between cold Cs Rydberg atoms. Phys. Rev. A 76, 011403 (2007)
Fermi, E. Sopra lo spostamento per pressione delle righe elevate delle serie spettrali. Nuovo Cimento 11, 157–166 (1934)
Greene, C. H., Dickinson, A. S. & Sadeghpour, H. R. Creation of polar and nonpolar ultra-long-range Rydberg molecules. Phys. Rev. Lett. 85, 2458–2461 (2000)
Stwalley, W. C., Uang, Y.-H. & Pichler, G. Pure long-range molecules. Phys. Rev. Lett. 41, 1164–1167 (1978)
Leonard, J. et al. Giant helium dimers produced by photoassociation of ultracold metastable atoms. Phys. Rev. Lett. 91, 073203 (2003)
Regal, C. A., Greiner, M. & Jin, D. S. Lifetime of molecule-atom mixtures near a Feshbach resonance in 40K. Phys. Rev. Lett. 92, 083201 (2004)
Hamilton, E. L., Greene, C. H. & Sadeghpour, H. R. Shape-resonance-induced long-range molecular Rydberg states. J. Phys. B 35, L199–L206 (2002)
Liu, I. C. H. & Rost, J. M. Polyatomic molecules formed with a Rydberg atom in an ultracold environment. Eur. Phys. J. D 40, 65–71 (2006)
Fabrikant, I. I. Interaction of Rydberg atoms and thermal electrons with K, Rb and Cs atoms. J. Phys. B 19, 1527–1540 (1986)
Omont, A. On the theory of collisions of atoms in Rydberg states with neutral particles. J. Phys. France 38, 1343–1359 (1977)
Valiron, P., Roche, A. L., Masnou-Seeuws, F. & Dolan, M. E. Molecular treatment of collisions between a Rydberg sodium atom and a rare-gas perturber. J. Phys. B 17, 2803–2822 (1984)
de Prunelé, E. Coulomb and Coulomb-Stark Green-function approach to adiabatic Rydberg energy levels of alkali-metal—helium systems. Phys. Rev. A 35, 496–504 (1987)
Greene, C. H., Hamilton, E. L., Crowell, H., Vadla, C. & Niemax, K. Experimental verification of minima in excited long-range Rydberg states of Rb2 . Phys. Rev. Lett. 97, 233002 (2006)
Bahrim, C., Thumm, U. & Fabrikant, I. I. 3Se and 1Se scattering lengths for e- + Rb, Cs and Fr collisions. J. Phys. B 34, L195–L201 (2001)
Bhatti, S. A., Cromer, C. L. & Cooke, W. E. Analysis of the Rydberg character of the 5d7d 1D2 state of barium. Phys. Rev. A 24, 161–165 (1981)
Li, W., Mourachko, I., Noel, M. W. & Gallagher, T. F. Millimeter-wave spectroscopy of cold Rb Rydberg atoms in a magneto-optical trap: quantum defects of the ns, np, and nd series. Phys. Rev. A 67, 052502 (2003)
Le Roy, R. J. LEVEL 8.0: A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasibound Levels. Chemical Physics Research Report CP-663, 〈http://scienide2.uwaterloo.ca/~rleroy/level/〉 (University of Waterloo, 2007)
Heidemann, R. et al. Evidence for coherent collective Rydberg excitation in the strong blockade regime. Phys. Rev. Lett. 99, 163601 (2007)
Molof, R. W., Schwartz, H. L., Miller, T. M. & Bederson, B. Measurements of electric dipole polarisabilities of the alkali-metal atoms and the metastable noble-gas atoms. Phys. Rev. A 10, 1131–1140 (1974)
Calef, D. F. & Wolynes, P. G. Smoluchowski-Vlasov theory of charge solvation dynamics. J. Chem. Phys. 78, 4145–4153 (1983)
Fabrikant, I. I. Theory of negative ion decay in an external electric field. J. Phys. B 26, 2533–2541 (1993)
Khuskivadze, A. A., Chibisov, M. I. & Fabrikant, I. I. Adiabatic energy levels and electric dipole moments of Rydberg states of Rb2 and Cs2 dimers. Phys. Rev. A 66, 042709 (2002)
Du, N. Y. & Greene, C. H. Interaction between a Rydberg atom and neutral perturbers. Phys. Rev. A 36, 971–974 (1987)
Barbier, L., Djerad, M. T. & Chéret, M. Collisional ion-pair formation in an excited alkali-metal vapor. Phys. Rev. A 34, 2710–2718 (1986)
Reetz-Lamour, M., Amthor, T., Deiglmayr, J. & Weidemüller, M. Rabi oscillations and excitation trapping in the coherent excitation of a mesoscopic frozen Rydberg gas. Phys. Rev. Lett. 100, 253001 (2008)
Johnson, T. A. et al. Rabi oscillations between ground and Rydberg states with dipole-dipole atomic interactions. Phys. Rev. Lett. 100, 113003 (2008)
Löw, R. et al. Apparatus for excitation and detection of Rydberg atoms in quantum gases. Preprint at 〈http://arxiv.org/abs/0706.2639〉 (2007)
Acknowledgements
We would like to thank C. Greene and J. M. Rost for discussions and P. Kollmann for his contribution in the early stage of the experiment. This work is supported by the Deutsche Forschungsgemeinschaft as part of the SFB/TRR21 and under contract PF 381/4-1, and by the Landesstiftung Baden-Württemberg. B.B. acknowledges support from the Carl Zeiss foundation and J.P.S. thanks the Alexander von Humboldt foundation for financial support.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
About this article
Cite this article
Bendkowsky, V., Butscher, B., Nipper, J. et al. Observation of ultralong-range Rydberg molecules. Nature 458, 1005–1008 (2009). https://doi.org/10.1038/nature07945
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature07945
This article is cited by
-
Scalable quantum processors empowered by the Fermi scattering of Rydberg electrons
Communications Physics (2023)
-
Quantum transports in two-dimensions with long range hopping
Scientific Reports (2023)
-
From Atomic Physics to Superatomic Physics
Journal of Cluster Science (2023)
-
Observation of a molecular bond between ions and Rydberg atoms
Nature (2022)
-
Experimental realization of a 3D random hopping model
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.