1. Program for Evolutionary Dynamics, Departments of Organismic and Evolutionary Biology, Mathematics, and Applied Mathematics, Harvard University, Cambridge, Massachusetts 02138, USA
2. Harvard-MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, Massachusetts, USA
3. Department of Zoology, University of British Columbia, Vancouver, British Columbia V6T 1Z4, Canada

Correspondence to: Erez Lieberman^1,2 Correspondence and requests for materials should be addressed to E.L. (Email: erez@erez.com).

Abstract

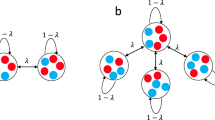
Evolutionary dynamics have been traditionally studied in the context of homogeneous or spatially extended populations^{1, 2, 3, 4}. Here we generalize population structure by arranging individuals on a graph. Each vertex represents an individual. The weighted edges denote reproductive rates which govern how often individuals place offspring into adjacent vertices. The homogeneous population, described by the Moran process³, is the special case of a fully connected graph with evenly weighted edges. Spatial structures are described by graphs where vertices are connected with their nearest neighbours. We also explore evolution on random and scale-free networks^{5, 6, 7}. We determine the fixation probability of mutants, and characterize those graphs for which fixation behaviour is identical to that of a homogeneous population⁷. Furthermore, some graphs act as suppressors and others as amplifiers of selection. It is even possible to find graphs that guarantee the fixation of any advantageous mutant. We also study frequency-dependent selection and show that the outcome of evolutionary games can depend entirely on the structure of the underlying graph. Evolutionary graph theory has many fascinating applications ranging from ecology to multi-cellular organization and economics.

MORE ARTICLES LIKE THIS

These links to content published by NPG are automatically generated.