Introduction

Estimating the shape of the pollen dispersal distribution is a critical issue for plant population biology (Austerlitz et al., 2004), because that distribution determines the effective size of the local breeding neighbourhood (Wright, 1943). Standard estimation techniques rely on the assumption of isotropic pollen dispersal (for example, Burczyk et al., 2002; Austerlitz et al., 2004), but prevailing wind directions are rather common, and the isotropic assumption may be too limiting for wind-pollinated species. Few studies have been carried out that considered the subject in detail, and these are with contrasting results. On the basis of a data set of phenotypic markers (Bateman, 1947, Tufto et al. (1997) used a Brownian motion model to show that pollen dispersal in an experimental planting of maize was anisotropic. Shen et al. (1981) reported an effect of wind direction on pollen flow in a Scots pine seed orchard. Meagher et al. (2003) showed directional pollen flow in a wind-pollinated transgenic grass cultivar, Agrostis stolonifera. In contrast, others have found little anisotropy in wind-pollinated tree species (for example, Burczyk et al., 1996, 2004; Burczyk and Prat, 1997; Lian et al., 2001; Robledo-Arnuncio and Gil, 2005). Moreover, Klein et al. (2006) encountered no tendency towards anisotropy for oilseed rape, a crop species with a mixed (insect and wind) pollination system. Thus, we see that anisotropy is possible, but not inevitable.

Many population biologists have expressed concern that landscape fragmentation is decreasing the size of local populations and reducing genetic connectivity among them (for example, Ledig, 1992; Young et al., 1996; Nason et al., 1997; Couvet, 2002), and anisotropy, if present, could increase that threat. Temperate tree species may be particularly sensitive to such changes, because historical population sizes have been large, and a sudden reduction in local population size can increase the possibility of inbreeding and inbreeding depression. In addition, if the fragmented populations are spatially isolated, the lack of gene flow could contribute to a loss of genetic variation (for example, Fernández-M and Sork, 2007), especially in the long term (Lowe et al., 2005). Under other circumstances, fragmentation promotes gene flow among fragments, because the lack of vegetative cover facilitates more extensive pollen flow, especially when the fragments are not far apart (for example, Young et al., 1996). Under those conditions, anisotropy can increase gene flow among some fragments and restrict it among others.

One of the key elements of connectedness among populations will be the modelling of the pollen dispersal curve and the potential for a long tail (Nichols and Hewitt, 1994). Early methods utilized paternity analysis to model the pollen curve over a restricted sample area and then assigned the progeny with unidentified fathers to gene immigration (for example, Adams and Birkes 1991; Adams et al., 1992). Using variations on this basic theme, several methods have been proposed to estimate the pollen dispersal curve (for example, Burczyk et al., 1996, 2002; Smouse et al., 1999; Oddou-Muratorio et al., 2005), although not with any particular attention to the issue of anisotropy. Examination of empirical studies (for example, Streiff et al., 1999; Burczyk et al., 2002; Meagher and Vassiliadis, 2003), suggests that individual maternal trees will receive the majority of their pollen from local pollen donors, the rest of the pollen being contributed by many individuals located further away. None of these studies examined the variance in the dispersal curve owing to anisotropy; yet this factor could interact with connectivity by either increasing or decreasing the variance in dispersal, depending on the direction.

Despite the value of paternity analysis in describing the pattern of pollen dispersal, it requires a large sampling effort, involving the maximum possible fraction of the potential fathers of a given set of seeds, which makes it difficult to sample on a landscape scale (Sork et al., 1999; Smouse and Sork, 2004; but see Oddou-Muratorio et al., 2005). To improve the scale of sampling and to provide an alternative method for the instances where genetic resolution is limited and/or where enumeration and sampling of the bulk of the paternal candidates is not feasible, an alternative method (dubbed TWOGENER) has been developed (Smouse et al., 2001). This method consists of computing the genetic differentiation between the pollen clouds of a large sample of mothers, physically spread across the landscape, and it requires only the genotypes of these mothers, along with those of a sample of seeds from each of them. Assuming an isotropic pollen dispersal curve that is either exponential or normal, this method can be used to estimate the average distance of pollen dispersal (Austerlitz and Smouse, 2001). We subsequently extended this TWOGENER approach to estimate the mean dispersal distance (δ) parameter, along with the effective density of reproductive adults, de (Austerlitz and Smouse, 2002). In a more recent effort, we have extended the treatment to estimate both scale and shape parameters of the dispersal curve, by extending the isotropic treatment to several two-parameter families, in particular the exponential power family of distributions (Austerlitz et al., 2004). Empirical studies show that paternity and TWOGENER analyses yield similar estimates (Austerlitz et al., 2004; Burczyk and Koralewski, 2005), but we have no idea of the bias that may occur when these isotropic methods are used in situations of strongly directional pollen dispersal.

Our main objective in this paper is to develop an anisotropic extension of the TWOGENER dispersal-curve extraction, which allows us to infer both the major axis of pollen dispersal, and the standard deviation of dispersal along this axis, as well as that along the orthogonal axis, assuming that pollen dispersal follows a bivariate normal distribution that is anisotropic. We also develop a permutation method that allows us to test the significance of this estimate. We then apply this method to test for wind-related anisotropy in a population of Quercus lobata occurring in an oak-Savannah ecosystem of southern California. Finally, we perform a simulation study, which is by no means exhaustive, but which evaluates the extent to which anisotropy can be detected in a design such as that we have used here. The parameters of our simulated populations were chosen to be as close as possible to those of the study population and to test these parameters under similar and contrasting spatial arrays of trees, so that we can assess both the bias and precision (variance) of our estimates under natural conditions and the power and robustness of our permutation method.

We apply this approach to anisotropic pollen movement to California valley oak (Q. lobata), a threatened tree species from the Central Valley of California that has undergone dramatic demographic attrition owing to habitat conversion and low adult recruitment rates in remaining populations since early European settlement in the 19th century (Pavlik et al., 1991). The species now occurs mainly in open savannahs in valleys and foothills of the Coast Ranges and Sierra Nevada mountains, and to a lesser extent in narrow gallery forests of the Central Valley. Conservation of this species has become a priority for the State of California, and estimation of gene flow rates and distances are a prerequisite for effective management of its genetic diversity. Our studies indicate that average pollen dispersal distance for savannah populations of Q. lobata ranges between 64 to 350 m, the precise value depending on the family of dispersal curves assumed, as well as the estimate of the effective adult reproductive density, de (Sork et al., 2002; Austerlitz et al., 2004). Because of the low adult density, all the estimates indicate a small reproductive neighbourhood size.

This wind-pollinated species seems a possible candidate for directional pollen movement. Detailed anemometer data from a nearby meteorological station document strong prevailing winds during the pollination season (Dutech et al., 2005). If wind direction has a significant effect, the orientation of populations and the primary direction of pollen flow should be taken into account in estimating the effective number of pollen donors per female tree. In a separate study of spatial genetic pattern of adults at this same study site, Dutech et al. (2005) found suggestive (though non-significant) evidence of anisotropic spatial autocorrelation. Those adults were all established between 400 and 100 years ago, and the population has experienced a long period of gradual demographic attrition, so we speculated that an initial anisotropic signature might well have decayed over time and that we might expect to find a stronger ‘wind signature’ among new recruits (Dutech et al., 2005).

Methods

Anisotropic TWOGENER

In the interest of mathematical tractability, we restrict ourselves here to the case of the bivariate anisotropic normal pollen dispersal kernel. Our previous studies have shown that it is clearly not the best-fitting curve in many cases (Austerlitz et al., 2004), but the possibility of deriving explicit closed-form formulas makes it a tractable starting point for any attempt to develop a method of detecting anisotropy, without resorting to strictly numerical analysis. This pollen dispersal distribution is characterized by three parameters, α, σmax and σmin. The first parameter (α) corresponds to the angle between the north–south axis and the major axis of observed pollen dispersal (rotating clockwise). The second is the standard deviation (σmax) of pollen dispersion along this major axis, and the third is the standard deviation (σmin) of pollen dispersion along the minor (perpendicular) axis.

As an angle between two axes, α can take values between 0° and 180° (0 to π radians). For a wind-pollinated species, the natural expectation is that the major axis of pollen flow (α) should be similar to that of the prevailing wind direction. More precisely, we assume that pollen disperses with equal probability to any point of an ellipse, for which the major axis makes an angle α with the Y axis and for which dispersion along the major and minor axes are proportional to the values of σmax and σmin, respectively (Figure 1). The classical equations describing an ellipse in a Cartesian system yield

Figure 1
figure 1

Schematic representation of the dispersal parameters of the dispersal curve. The probability of pollen dispersal is the same for every point on the represented ellipse. α, σmax and σmin correspond, respectively, to the major dispersal axis, the standard deviation of dispersal along this major axis and the standard deviation of dispersal along the minor axis.

Full size image

When σmax=σmin, all terms containing the angle α cancel, reducing Equation (1) to its isotropic bivariate form, where pollen disperses with equal probability to any point on a circle around the origin. We computed the average dispersal distance δ (integrated around the ellipse) for the anisotropic distribution, using MATHEMATICA (Wolfram, 1999), as

where E(m) denotes the complete elliptic integral, defined as

for any nonnegative m value. While δ cannot be computed in closed form, numerical integration is easily accomplished, and the MATHEMATICA software program does that routinely, with the function EllipticE. This integration is also performed automatically in the software program that we provide (see below), which does not require the installation of MATHEMATICA.

As in our previous studies, the estimates that we develop here are based on the TWOGENER method (Smouse et al., 2001), where the level of differentiation (φij) between the pollen clouds is computed for all pairs of females for which seeds have been sampled in the population (Austerlitz and Smouse, 2002; Austerlitz et al., 2004). For each of these pairs, the observed level of pollen pool genetic differentiation (φij) is compared with the theoretical level of differentiation expected between these two females, a distance zij apart. For isotropic distributions, the theoretical expectation for φij value between the ith and jth females is dependent only on the parameters of the dispersal curve, the effective adult reproductive density (de) and the physical distance (zij) between them (Austerlitz et al., 2004). Where direction matters, this theoretical φij will also depend on the angle (θij) made by the line that joins these two females, relative to the Y axis (see Figure 2).

Figure 2
figure 2

The two physical quantities that are computed between the ith and jth mothers, their physical distance of separation (zij) and the angle they make with the Y axis (θij).

Full size image

The equation for the pairwise φij for two females at distance zij, making an angle θij with the Y axis is computed, following Austerlitz and Smouse (2001), as

where Q0(dα,σmin,σmax) is the probability that two male gametes, sampled from the pollen cloud of the same female, were drawn from the same father; Q(d,α,σmin,σmax,zij,θij) the probability that two male gametes, sampled from the pollen clouds of the ith and jth females, were from the same father. It develops that Q0(d,α,σmin,σmax) can be computed directly, using Equation (10) from Austerlitz and Smouse (2001) as

where p(α,σmin,σmax;x,y) is the dispersal distribution defined in Equation (1). Q(d,α,σmin,σmax,zij,θij) can be computed as

Note that, as in our previous models (Austerlitz and Smouse, 2001; Austerlitz et al., 2004), Equations (3) and (4) are based on the assumptions that the reproductive trees are randomly distributed on the landscape, following a point process pattern. We also assume that these adults are not inbred, and that there is also no biparental inbreeding. The integrals involved in Equations (4 and 5) are computable analytically, using Mathematica 4.1, and their expressions can be inserted into Equation (3), yielding (after further simplification):

The dispersal parameters α, σmax and σmin can be estimated by numerically minimizing the squared-error loss criterion for the choice of these parameters,

where nm is the number of sampled mothers. The effective reproductive density (d) can be set to a fixed value, usually the adult census density of the population, or it can be estimated jointly with the dispersal parameters. The standard deviation of each estimate was computed by jack-knifing among loci (Weir, 1996).

The level of anisotropy was computed as the ratio Ra=σmax/σmin. Two Ra values can be estimated, one (R̂a1) with d fixed at the census density and one (R̂a2) with d jointly estimated. We tested the significance of both R̂a values with a simulation approach. For this, we estimated their null distribution by generating 1000 simulated data sets based on the hypothesis of isotropic dispersal. The simulations were performed with the simulation method described below, using as inputs the spatial positions of the mothers and the potential fathers (including the non-genotyped ones) and the genotypes of the mothers. For the potential fathers, the genotypes were completed when partially known or created when completely unknown, by drawing their alleles at each locus according to the estimated allelic frequencies within the population. For the null distribution of Ra1, the simulations were performed assuming an isotropic normal distribution with parameter σ1, where σ1 represents the estimated value of σ from TWOGENER assuming an isotropic dispersal and fixed density. For Ra2, we used an isotropic normal distribution with parameter σ2, where σ2 represents the estimated value of σ from TWOGENER assuming an isotropic dispersal with density jointly estimated. Then, the tail probability of each estimated R̂a value was computed as the proportion of values in the null distributions that were above the actual data result. Note that this method requires the spatial positioning of the adults several hundreds of metres around the sampled mothers, but not their genotyping.

Note also that the pollen dispersal distribution given in Equation (1) is centred on zero. It means that, while we can predict a main axis of pollen dispersal, we cannot predict directionality. For instance, we can say that the main dispersal axis makes a 10° angle with the North–South axis, but we cannot assess whether the main wind comes from the south or the north. This constraint comes from the symmetry in the TWOGENER pairwise Φft coefficients: for each pair of mothers A and B, we can compute only one Φft value, and this value will be the same whether the wind blows mostly from A to B or from B to A.

Software programs for all of the methods described here are available in the POLDISP package (Robledo-Arnuncio et al., in press), available at http://poldisp.googlepages.com/.

A case study in Valley oak

Study site and sampling regime

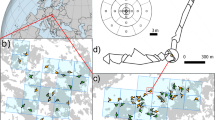
The study site is located at the U.C. Santa Barbara University of California's Sedgwick Reserve, along Figueroa Creek (34°42′N, 120°02′W), 10 km northeast of Santa Ynez, in Santa Barbara County, California (Sork et al., 2002). Valley oaks at our study site occupy deep alluvial soils on the valley floor and adjacent hill slopes, at elevations ranging from 300 to 400 m above sea level (Figure 3). The valley is oriented roughly 5°–10° west-of-north to east-of-south, and is bounded by ridges ranging in elevation from 440 to 475 m above sea level. The current adult stem density of Valley oak in the study area averages about 1.19 trees/ha at Figueroa Creek, and most individuals are greater than 85 cm diameter at breast height, representing adults that are probably at least 150 years of age.

Figure 3
figure 3

Map of the study population in Figueroa Valley at Sedgwick Reserve, Santa Barbara Co., CA, USA, with all adult trees indicated by white dot and sampled trees circled.

Full size image

Since 1997, the Sedgwick Reserve has maintained a weather station located on a level terrace, approximately 1 km (750–1500 m) west of our study population. We analysed hourly average wind speed and direction for daytime hours (0900–1800, PST) during the main flowering period of 1 March to 30 April 2001, the year of this study (Figure 4). During the flowering period, wind speeds averaged 3.2±1.6 m/s, with maximum hourly averages of 7–8 m/s. The wind rise shows the strong directionality of winds from the west-northwest, the main wind axis being 290°, which is true for most low-elevation locations in the Santa Ynez Valley (see for example, Ogden, 1975). Relative to the weather station, wind speeds in the study area may be reduced slightly by the sheltering effect of local topography, but the direction should be much the same.

Figure 4
figure 4

Wind rose describing the direction and velocity of wind during the main flowering period of the study year 2001 between 0010 and 0018.

Full size image

In the fall of 2001, we sampled acorns from as many trees as possible in the Figueroa Creek area, obtaining seeds from 31 maternal trees (Figure 3). The average distance between sampled maternal trees was 865 m; minimum distance was 13 m and maximum distance was 3198 m. The collected acorns were conveyed to the University of Missouri (St Louis, CA, USA) and planted in a greenhouse for germination. We collected one leaf per seedling for DNA analysis. The number of seedlings analysed per family ranged from 5 to 12 (mean=8.72).

DNA analysis

We extracted total DNA from 30 to 40 mg of leaf tissue from each individual (offspring and mother trees), using a CTAB (cetyltrimethylammonium bromide) buffer and liquid nitrogen, following the method described in Sork et al. (2002). We utilized a battery of six microsatellite loci, originally developed from other oak species: QrZAG20, QpZAG36, QpZAG46 and QpZAG110 developed by Steinkellner et al. (1997) from Q. robur and Q. petraea; MSQ4 developed by Dow et al. (1995) from Q. macrocarpa; JFF58, which is a redesign of the QpZAG58 primer pair (Steinkellner et al., 1997) performed by JF Fernández-M (unpublished data). The sequence of the new forward primer is ATCCATTATCTGCAAGATTC and the reverse primer is TCTTCTCTTTTCTTTTTCCT. QrZAG20, QpZAG36, QpZAG110 and MSQ4 were used to describe spatial genetic structure of adults at Sedgwick Reserve (Dutech et al., 2005). We used PCR methods and visualization on denaturing acrylamide gels, as described by Sork et al. (2002), to reveal polymorphism at these microsatellite loci. We genotyped all 31 mothers and their offspring for these six loci, along with 57 other adults, to have a reliable estimate of allelic frequencies for each of the loci, needed for the TWOGENER analysis.

Empirical results

The global differentiation of the pollen clouds was low (Φft=0.040). First assuming isotropic dispersal and setting effective reproductive density equal to average adult density (d) for our Figueroa Creek site (d=1.19 trees/ha), we estimated an isotropic normal dispersal standard deviation for pollen dispersal of ς̂=88.6 m, which corresponds to a mean dispersal distance (δ̂) of 111 m (Austerlitz and Smouse, 2001). The joint estimation of effective density and dispersal distance yielded a larger value for dispersal distance (ς̂=193 m, δ̂=242 m), along with an estimated effective density (d̂e) of 0.616 individuals per ha, so (d̂e/d)=∼0.5.

Using the anisotropic Gaussian dispersal model described above, we obtained an estimate of the angle made by the major dispersal axis with the north axis (α̂) of 154°±2.63°, along with a standard deviation of dispersal, along this axis (ς̂max) of 185±29 m, as well as a minor axis ς̂min of 42±3 m (Figure 5). From Equation (2), these estimates yielded an estimated mean pollen dispersal distance of δ̂=151±22 m, slightly above the value obtained with isotropic dispersal. The estimated ratio of standard deviations, R̂a=(ς̂max/ς̂min) was 4.39, not significant (P=0.4) with the permutation method. When density was jointly estimated with the dispersal parameters, it was estimated to be d̂e=0.674±0.399 trees/ha, and using that as our density estimate, we obtained ς̂max=233±224 m, ς̂min=56±12 m, α̂=152°±7.22° and δ̂=264±178 m. These figures yield R̂a=4.12, also not significant (P=0.43).

Figure 5
figure 5

Elliptic representation of the dispersal function (see Figure 1) where density is set at its fixed value. The dashed line represents the main wind direction (see Figure 4).

Full size image

Simulation study

Procedures

We performed a simulation study, designed to mimic the Valley oak study, to assess the power and robustness of the anisotropic analysis. We simulated a spatially explicit population of 314 individuals (the number of adults at the Figueroa Creek site; see Figure 3). All individuals were characterized according to their spatial coordinates and their genotypes at the six loci used above. The spatial coordinates were strictly the same as in the study population. We had the complete six-locus genotypes of the 88 individuals (31 mothers and 57 other adults) that we used for the empirical analysis above. We had another 162 adults with only four of the six loci from Dutech et al. (2005). These four-locus genotypes were held as is, with the other two loci being drawn at random from a Hardy–Weinberg gene pool formed with the allelic frequencies from the 88 previous individuals. We had another 160 for which we had spatial locations, but no genotypes, and for these, we drew six-locus genotypes from the Hardy–Weinberg gene pool. We also had a few holes in the data (missing loci), which were filled by random draws from the Hardy–Weinberg gene pool.

Then we simulated progenies for a given number (nm) of chosen mothers, following the procedure explained by Austerlitz and Smouse (2002). Briefly, assume that pollen follows a dispersal distribution p(Ω; x, y), where Ω={α, σmax, σmin} is the set of dispersal parameters under discussion. We assumed equal male fecundities, so that the pollination probabilities were determined by the array of intermate distances only. The likelihood, pmi, of the male at position (xi, yi) providing the gamete fertilizing an ovule for a female at position (xm, ym) is

which assumes that the probability of fertilizing a given female depends only on the distance to that female, and so that every individual has the same male fertility. The genotype of the resulting offspring is constituted by first drawing its father, according to the pmi, and then assigning a pair of gametes, one from each parent, in Mendelian proportions.

We performed simulation analyses of three different dispersal functions. First, we used an anisotropic dispersal model, with parameters α=154°, σmax=186 m and σmin=42 m, as estimated from the empirical data (see Case study). Second, we used a dispersal function with the same values of σmax and σmin, but with an angle α=64°, orthogonal to that major axis, to determine whether we could have detected anisotropy had the major axis been rotated 90o. This rotation tests whether our observed result was an artifact of the peculiar spatial arrangement of trees in our sample, which differs to some extent from the random spatial point process assumed in Equations (4) and (5). Indeed the distribution of the trees in our population is not random, because most mother trees sampled here are situated along a North–South line, running roughly down the valley and also close to the main wind direction (see Figures 3 and 4). Thus, this rotation allows us to assess whether the particular orientation of the trees, relative to the main wind direction could generate some bias. Third, to determine how often spurious anisotropy would be detected in the isotropic case (type-I error rate), we used an isotropic dispersal distribution with σ=125 m (set to the same average dispersal distance as for the first case).

To assess the effects of the number of mothers sampled (nm) and of the progeny size per mother (np), we assumed either nm=31 or 62 and np=20 and 40. For nm=31, we used the 31 mothers of the experimental studies, whereas for nm=62, we added 31 mothers drawn at random (the same for all the simulations). This simulation allowed us to determine whether accuracy was augmented more by doubling the number of sampled mothers or their progeny sizes.

We performed repeated simulations (1000 replicates) for each case. For each simulated data set, we first estimated σ for the isotropic bivariate normal case, with adult density fixed either at its observed value or estimated jointly with the dispersal parameters. Second, we estimated the anisotropic parameters, either setting density at its observed value or estimating it jointly with the dispersal parameters. For all simulations, we computed the bias, standard deviation and the root mean-squared error () of the estimates. Then, for each simulated data set, we computed the ratio Ra of major to minor axis σ estimates, both with density set at its observed value and jointly estimated with the other parameters. We applied the simulation based testing method to each of these simulated data sets, allowing us to determine the proportion of cases in which anisotropy was detected at the 5% level, both in situations where dispersal was truly anisotropic and in situations where it was not, to assess both type-I and type-II error rates, thus evaluating both the power and robustness of our treatment.

Results

Consider first the case (Table 1), for which we used parameters similar to those estimated from the field study (α=154, σmax=186 m and σmin=42 m). The estimates of δ obtained under the assumption of isotropic dispersal and with density set at its observed value exhibited negative bias for all sample sizes. This bias was constant with increasing np, but increased with increasing nm, whereas the standard deviation decreased with both np and nm, yielding an overall increase of the . When density was jointly estimated, the procedure yielded an upward bias for d̂e, except for the largest sampling effort (nm=62 and np=40). The dispersal distance (δ̂) jointly estimated with d̂e showed a negative bias and a larger than when density was fixed. This decreased when nm or np increased, with np having the stronger impact. It reached a reasonable value (30%) only for the largest sampling effort.

Table 1 Bias, standard deviation and root mean-squared error () of the various estimates of the dispersal parameters for four combination of the number of mothers (nm) and the progeny size (np) based on field study estimates
Full size table

Consider now the estimates obtained under the correct assumption of anisotropic dispersal, with density set at its observed value. The main dispersal angle (α) was always correctly estimated with minimal bias and MSE, and increasing either the number of mothers (nm) or the progeny size (np) had little effect. The estimated dispersal along the main axis (ς̂max) showed high upward bias (∼67%) and (∼87%) for the lowest sample size. Bias and decreased with the sample size, the decrease being slightly higher when nm was doubled than when np was doubled. The dispersal along the orthogonal axis (ς̂min) showed lower relative bias and than ς̂max for the lowest sample sizes. However, while these bias and decreased with increasing np as expected, this was not the case with increasing nm, where it remained either constant or even increased. Thus, the relative bias was higher for ς̂min than for ς̂max for the highest values of nm and np. As a whole, the of the estimate of dispersal distance (δ̂) always decreased with increasing sample size, the effect being slightly stronger for a doubled nm than for a doubled np, as for ς̂max. The unexpected behaviour of ς̂min might be a consequence of a trade-off, the increase of the precision of ς̂max and δ̂ being obtained in some cases at the cost of a small loss of precision for ς̂min.

When density was estimated jointly with the dispersal parameters, the estimates of these dispersal parameters (ς̂max, ς̂min and α̂), and thus of average dispersal distance (δ̂), showed approximately twice as much bias and as for the case where density was fixed. The impact of an increasing nm and/or np was the same as above. Regarding the estimated density (d̂e), it showed quite a large (∼52%) for the minimal values of nm and np, but much less than when isotropic dispersal was assumed for the estimation. This high of d̂e decreased strongly with an increase of np, but not so much with an increase of nm.

The simulations performed with an anisotropic dispersal distribution, with the same σmax and σmin as before, but with a α parameter of 64°, showed similar results (Table 2), the biases and being higher in some cases but lower in others.

Table 2 Bias, standard deviation and root mean squared error () of the various estimates of the dispersal parameters for four combination of the number of mothers (nm) and the progeny size (np) with α=64°
Full size table

For simulations performed with isotropic dispersal (Table 3), isotropic estimates behaved as expected. We observed a decrease of bias and with increasing nm or np. When anisotropic dispersal was assumed for estimation, so that we might anticipate dissimilar estimates of σmax and σmin, there was an upward bias for σmax and thus for δ, but bias decreases with increasing progeny sample size; σmin showed only limited bias. When density was fixed, the decrease in bias and was stronger for an increase of np than for an increase of nm, whereas the opposite pattern occurred when density was jointly estimated. As expected, the estimate of α showed considerable variance, which does not decrease with sample size, since there is no particular value of α that is true in the isotropic case.

Table 3 Bias, standard deviation and root mean squared error () of the various estimates of the dispersal parameters for four combination of the number of mothers (nm) and the progeny size (np) for isotropic dispersal
Full size table

Power of the method

Considering first the simulations where dispersal was truly anisotropic (α=154° or 64°, σmax=186 m and σmin=42 m), we observed an increased probability of detecting anisotropy at the 5% or the 1% level with either increasing nm or np (Table 4). For the minimal sample size (nm=31 and np=20), the probability of detecting anisotropy was low for both values of α, whether density was fixed or jointly estimated. An increase of np yielded generally a higher increase of the probability of detecting anisotropy than an increase of nm. To detect anisotropy when density was jointly estimated required substantial amounts of data, it could only be detected in about half of the cases when np was doubled, and it was only for the maximal sample size (nm=62 and np=40) that it could be detected in a large majority of cases. Considering simulations with isotropic dispersal, spurious anisotropy was usually detected in a proportion close to the expected 5% or 1% level, for all values of nm and np.

Table 4 Proportion of cases where anisotropy is detected at the 5% level (P<0.05) or the 1% level (P<0.01) in the simulated data sets for the three assumed dispersal functions and four combination of the number of mothers (nm) and the progeny size (np), when density is either set at its known value or jointly estimated with the dispersal parameters
Full size table

Discussion

Anisotropy in Valley oak pollen flow

We find only a slight tendency towards anisotropy of pollen dispersal here, despite a strong prevailing wind direction for the region. Our estimates were non-significant, which is consistent with our simulation study, showing that it is quite difficult to detect anisotropy with progeny sizes of less than 20 offspring per mother. Also consistent with the simulation study, we found that the standard deviations of the estimates were low for α and σmin, but much higher for σmax. The inferred main direction estimated either with fixed density (α̂=154°, s.d.=2.63°) or with density jointly estimated (α̂=152, s.d.=7.22°), was not coincident with the main wind direction (112o). This discrepancy suggests that pollen movement may be influenced by very localized wind patterns. On the basis of the results of our simulation study, it does not seem that the angle we detected is a consequence of the specific spatial arrangement of trees. However, if the orientation of the valley modifies the local directionality of wind and if the spatial heterogeneity of trees modifies the aerodynamics of pollen movement, the angle α may not conform to the prevailing regional wind direction. In the case of Valley oak, we will need a larger data set to assess the angle and standard deviation of the directionality of the pollen flow. Increasing the number of mothers, in particular, will probably reduce the impact of the local effects, providing a more general trend.

As a comparison, we also evaluated anisotropy in our study population with the NEIGHBOR method of Burczyk et al. (1996). This method also failed to detect a significant level of anisotropic dispersal, and the non-significant tendency (60° from the North axis) was also quite different from the main wind direction, again highlighting a need for more data. With either analysis, however, the signal is weak and non-significant, and neither approach indicates that pollen movement is strongly directional in this population of valley oak.

One motivation for this study was to test whether the subtle (and non-significant) anisotropy identified in the adult population of Valley oak (Dutech et al., 2005) was consistent with anisotropy in the progeny population. For adult genotypes, the major axis of orientation was α =106.5°, about 6°–7° ‘off the wind.’ In that study, we speculated that the anisotropic signal was weakened as the seedling populations aged into adult populations. However, we now observe for the progenies that the pollen orientation is even further ‘off the wind.’ This discrepancy might be the consequence of the imprecision induced by the limited sample sizes of both the adult and the offspring studies. Alternatively it could be caused by specific events that have occurred during the single year of study. Again it would be helpful to conduct a comparative study over several years, using the same mother trees and the same molecular markers, such as that performed by Irwin et al. (2003) for Albizia julibrissin or that for Sorbus torminalis by Oddou-Muratorio et al. (2005). Unfortunately, it is quite unusual for the same set of Q. lobata trees to produce acorns in consecutive years owing to the masting dynamics of most oaks (for example, Nakanishi et al., 2005), so such replications would require a long-term study.

For the moment, we can only compare our study with the previous study of pollen dispersal performed in this same population (Sork et al., 2002). Assuming a normal dispersal distribution and effective density based on the natural population, the estimated value of δ in this previous study was of 65 m. Here, assuming a fixed density as in this previous study, the Gaussian dispersal mean value of δ=110 m, which is a bit higher than observed in 1999 but the same order of magnitude. This limited difference between 1999 and 2001 might be due either to differences in sampling (more individuals in the centre of the population for 2001 sampling) or to differences in intensity of pollination between the 2 years. On the basis of these 2 years, we conclude so far that it does not appear that directional pollen flow is biasing our estimates of pollen flow.

Detecting anisotropy and estimating its level

Our simulation study illustrates both the possibility and the difficulty of demonstrating anisotropic pollen dispersal. It is possible to detect such anisotropy in pollen dispersal if it exists, using just the genotypic data on seed trees and their offspring, by way of TWOGENER extraction. The bias and for the dispersal parameters (σmax, σmin and α) are quite high with low numbers of offspring per mother, but they decrease readily when this number increases. σmax has higher bias and than α and σmin for low sample sizes, which means that more data are needed to estimate that parameter well. Our simulations show also that using the isotropic estimates while the true dispersal is anisotropic yields a systematic underestimation of mean dispersal distance of pollen (δ).

Regarding the impact of the shape of the population, it is interesting to note that in terms of bias and , and in terms of the power to detect anisotropy, our estimates performed about equally well with a major axis of pollen dispersal that parallels the main axis of distribution for the population (along Figueroa Creek) or orthogonal to it (across the Valley). So, we can conclude that this method is reasonably robust in detecting a predominant direction of pollination, even if the adult trees are preferentially distributed along a divergent axis. Moreover, our method is unlikely to detect excessive and spurious anisotropy when the true dispersal curve is isotropic. Because the percentage of these cases of spurious anisotropy detected (∼10%) is a bit higher than the 5% expected by chance, an anisotropic signal that would just be detected at or close to the 5% level should be considered with caution.

The progeny sample size needed to provide sufficient power depends on the strength of anisotropy, the degree of polymorphism of the genetic markers and the array of spatial positions occupied by the mothers, but if only ∼30 mothers are considered, at least 40 offspring each will be necessary to have a reasonable chance of detecting anisotropy (see Table 4). Unlike the situation for isotropic dispersal (Austerlitz and Smouse, 2002), increasing the number of mothers is, in most cases, less efficient than increasing the number of offspring. This may stem from the fact that, with a limited number of offspring, the φij values may, by chance, be elevated in one particular direction, yielding spurious anisotropy in the simulations performed under the isotropic model to obtain the null distribution, thus reducing the power to detect this anisotropy. Additional simulations will be needed to explore the sampling aspects more thoroughly.

Sample sizes for anisotropic analyses should be very large if the effective density is jointly estimated. The simulations performed here demonstrated that it is preferable for the investigator to provide some independent estimate of effective density, because it is much easier – especially for low sample sizes – to detect anisotropy when effective density is fixed. The trouble is that this estimate might be difficult to obtain, since many factors, such as spatial aggregation of the adults, phenological differences and differences in male fertility (see Meagher and Vassiliadis, 2003; Oddou-Muratorio et al., 2005), will affect the ratio of effective to observed density. Some effort to gain more information on these other factors would be quite valuable. Alternatively, it is possible to use the observed density or the density estimated under the isotropic model, with the caveat that the detection of the angle will have more power, but dispersal distance may be underestimated.

Another important issue concerns the family of dispersal curve assumed. Here, we assumed a bivariate normal pollen dispersal distribution for the sake of mathematical tractability. We have shown elsewhere that fat-tailed curves are more realistic in natural populations (Austerlitz et al., 2004). No closed-form analytical formulae are available for the φij for such curves, so while the results can be computed numerically, the methods are elaborate and computer-intensive, due to the number of parameters to be estimated for the anisotropic case (four or five, depending on whether density is or is not estimated jointly). Such methods will need further development in future work. Since our prime interest here is in detecting anisotropy, assuming that dispersal is normal might not be a bad place to start.

This extension of the TWOGENER modelling approach provides a promising avenue for the estimation of the degree of anisotropy in plant populations where directionality of pollen movement is a concern. This method differs substantially from the Neighborhood model that includes distance and directionality in modelling pollen flow (for example, Burczyk et al., 1996). The Neighborhood model essentially uses a parentage approach to identify pollen donors, and like all parentage approaches, relies on access to the genotypes of all potential pollen donors within a proscribed area around focal seed parents (Smouse and Sork, 2004). The Neighborhood model provides an estimate of the angle of directionality of pollen movement from pollen source to pollen recipient, whereas this TwoGener treatment provides the angle, but without respect to directionality, so treatment of the angular displacement is antisymmetric. Another difference in the two methods is that Neighbourhood model uses likelihood ratio criteria, which can be tested either with a χ2 approximation or a permutational procedure. The choice of methods must depend on the sampling design and the availability of paternal genotypes.

In conclusion, we have shown here that it is clearly feasible (with appropriate experimental designs) to detect anisotropy in pollen dispersal in natural populations, using a TWOGENER extraction. Our simulations indicate the need for greater replication, both within and among mothers, than provided with this particular data set. Our main objective here was to introduce a formal methodology. We have begun, with some limited simulations, to provide some hints concerning better sampling strategies, but this matter should be the subject of a specific study in the future. Detecting anisotropy is, in any case, a matter of some importance. Indeed, we show here that neglecting anisotropy yields an underestimate of the mean dispersal distance and an even greater underestimate of dispersal distance along the main axis.