Abstract
Purpose: There is ongoing debate about whether testing low-risk genes at multiple loci will be useful in clinical care and public health. We investigated the usefulness of multiple genetic testing using simulated data.
Methods: Usefulness was evaluated by the area under the receiver-operating characteristic curve (AUC), which indicates the accuracy of genetic profiling in discriminating between future patients and nonpatients. The AUC was investigated in relation to the number of genes assumed to be involved, the risk allele frequency, the odds ratio of the risk genotypes, and to the proportion of variance explained by genetic factors as an approximation of the heritability of the disease.
Results: We demonstrated that a high (AUC > 0.80) to excellent discriminative accuracy (AUC > 0.95) can be obtained by simultaneously testing multiple susceptibility genes. A higher discriminative accuracy is obtained when genetic factors play a larger role in the disease, as indicated by the proportion of explained variance. The maximum discriminative accuracy of future genetic profiling can be estimated at present from the heritability and prevalence of disease.
Conclusions: Genetic profiling may have the potential to identify individuals at higher risk of disease depending on the prevalence and heritability of the disease.
Similar content being viewed by others
Main
Testing single susceptibility genes is of limited value for the prediction of complex diseases, but there is ongoing debate about whether genetic profiling, testing at multiple loci, will be useful in clinical care and public health. Some predict that this will be an important step toward personalized medicine, in which the development of complex diseases can be predicted by simple DNA tests in which several genes are evaluated simultaneously.1,2 Others have maintained that genetic profiling will be of limited use for the prediction of complex genetic diseases, because hundreds of genes are likely involved, each conveying only a minor increase in risk.3,4 Although both camps have been accumulating support for their viewpoints, empirical studies that demonstrate the usefulness of predictive testing by genetic profiling are still lacking.
To be useful for the prediction of disease, genetic profiles should discriminate between subjects who will develop the disease and those who will not. The discriminative accuracy of dichotomous tests or qualitative traits is usually indicated by the combination of the sensitivity, the percentage of positive test results among subjects who will develop the disease; and the specificity, the percentage of negative test results among those who will not develop the disease. In case of a perfect test, all subjects who will develop the disease have a positive test result (sensitivity = 1.0), and all subjects who will not develop the disease have a negative test result (specificity = 1.0).
Genetic profiling is not a dichotomous test with positive and negative outcomes, but can be considered as a continuous test when the profiles are expressed by their associated disease risks.5 We have proposed that the usefulness of genetic profiling should be evaluated by the area under the receiver-operating characteristic (ROC) curve.5 The ROC curve presents the combinations of sensitivity and specificity for each possible cut-off value of the continuous test result that can be considered to define positive and negative test outcomes. The magnitude of the area under the receiver-operating characteristic curve (AUC) indicates whether a test is useful to identify individuals who are at increased risk of disease (screening; e.g., AUC ∼ 0.80) or to diagnose a disease before the onset of symptoms (presymptomatic diagnosis; e.g., AUC > 0.99).
Yang et al. demonstrated that a multiple genetic test consisting of 20 susceptibility genes with mutations conveying a 1.5–1.7-fold increase in risk may yield an AUC of 0.77.6 This level of discriminative accuracy is comparable to that of total serum cholesterol testing for the prediction of coronary heart disease and to neuropsychological testing for the prediction of Alzheimer's disease in asymptomatic individuals.7,8 Yet, it has been argued that for most common causes of morbidity and mortality in Western societies, such as cardio- and cerebrovascular disease, it is conceivable that hundreds of genes are involved, each conveying only a very small increase in risk (< 1.5-fold).3,4,9 Whether genetic profiling based on such a high number of weak predictors will yield a useful predictive test remains to be determined.
The aim of the present study was to investigate the discriminative accuracy of testing multiple low-risk susceptibility genes for the presymptomatic testing of complex diseases. Using simulated data, we evaluated the AUC as a function of the number of genes involved, the frequencies of the risk alleles and the strength of the relationships between genotypes and disease. Finally, we investigated the AUC in relation to the proportion of explained variance by genetic factors, which is an approximation of the total contribution of genetic factors to the disease (i.e., heritability).
METHODS
Modeling strategy
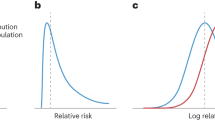
The discriminative accuracy, quantified as the AUC, is determined by the distribution of disease risks in those who will develop the disease and those who will not. The area under the ROC curve (AUC) indicates the discriminative accuracy of a continuous test.10 The AUC ranges from 0.5 (total lack of discrimination) to 1.0 (perfect discrimination) and is independent of the prevalence of disease.11 The AUC basically can be considered as the probability that the test correctly identifies the diseased subject from a pair of whom one is affected and one is unaffected. An AUC of 0.95 means that 95% of the pairs is correctly classified, whereas a test with an AUC is 0.50 is nondiscriminative – as accurate as tossing a fair coin. Figure 1 presents exemplary distributions of disease risks that correspond with AUCs ranging from 0.60–0.99. The figure shows that the distributions considerably overlap when the AUC is 0.60, but less when the AUC is ≥ 0.90. To obtain these distributions of disease risks under different conditions in our simulation studies, we need to specify: 1) the genetic profiles of all subjects; 2) the disease risks associated with the genetic profiles; and 3) the disease status of all subjects. These are modeled in three subsequent steps.
Modeling genetic profiles
In each simulation, we considered a disease for which we assumed that the genetic origin was fully understood and that all genes predictive for the onset of the disease were used to define the genetic profiles. We simulated genetic profiles that consisted of up to 400 genes. This number is arbitrary but corresponds to the number of genes linked to e.g., obesity.12 We assumed that each single gene had two alleles and that all genotypes and allele proportions were in Hardy-Weinberg equilibrium. Under this assumption, genotype frequencies for the single genes can be calculated from the allele frequencies. Genes were modeled to be independent, i.e., no linkage disequilibrium existed between genes. For the construction of the genetic profiles, we first created a vector for each gene with as many copies of the three genotypes as indicated by the genotype frequency and the sample size. Assuming that the genes segregate independently, we then sampled, randomly without replacement, for each subject a genotype from each vector.
Modeling disease risks associated with genetic profiles
In the next step, we calculated the disease risks associated with the genetic profiles using Bayes' theorem. Bayes' theorem states that the posterior odds of disease are obtained by multiplying the prior odds by the likelihood ratio (LR) of the test result; here, the genetic profile.13 The prior odds are calculated from the prevalence of disease  and the posterior odds are converted back into probabilities
and the posterior odds are converted back into probabilities  , which is the disease risk associated with the genetic profile.
, which is the disease risk associated with the genetic profile.
When a multiplicative risk model on the odds scale14,15 and no statistical interaction between the genes are assumed (i.e., no statistical interaction terms are included in the model), the LR of a genetic profile can be obtained by multiplying the LRs of the single genotypes. The LR of a single genotype is the percentage of the genotype among subjects who will develop the disease divided by the percentage of the genotype among subjects who will not develop the disease. This LR can be calculated from Table 1. We constructed this table for each gene. The marginal totals of this table are calculated from the prevalence of the disease (p), the allele frequency (f) and the sample size (n). We quantified the risks of disease associated with the genotypes of a single gene by the odds ratio (OR) of the heterozygous risk genotype (as compared to the homozygous wildtype), with the OR for the homozygous risk genotype being the square of the OR of the heterozygous genotype. In Table 1, the ORs of the homozygous and heterozygous risk genotypes define the ratios  and
and  Because both the marginal totals and the ratios were specified as model parameters, the values for a-f could be logically derived. From Table 1, we calculated the LR of homozygous risk genotype (EE) as
Because both the marginal totals and the ratios were specified as model parameters, the values for a-f could be logically derived. From Table 1, we calculated the LR of homozygous risk genotype (EE) as  of the heterozygous risk genotype (Ee) as
of the heterozygous risk genotype (Ee) as  and of homozygous wildtype (ee) as
and of homozygous wildtype (ee) as  Note that OREE =
Note that OREE =  and OREe =
and OREe = 
Modeling disease status
To model disease status, we used a procedure that compares the disease risk of each subject to a randomly drawn value between 0 and 1 from a uniform distribution.16 A subject was assigned to the group who will develop the disease when the disease risk was higher than the random value and to the group who will not develop the disease when the risk was lower than the random value. Hence, subjects with high disease risks are more likely to be assigned to the group who will develop the disease than those with low-risks.
Statistical analyses
The AUC was calculated from the distribution of disease risks of subjects who will develop the disease and of those who will not (Fig. 1). The AUC was obtained as the c-statistic by the function somers2, which is available in the Hmisc library of R software.16 The proportion of explained variance by genetic factors was calculated as  where risk indicates the disease risk conditional on the genetic profile and n the number of subjects in the study. All analyses were performed under SuSE 7.3 Linux using R software v 1.7.1.17
where risk indicates the disease risk conditional on the genetic profile and n the number of subjects in the study. All analyses were performed under SuSE 7.3 Linux using R software v 1.7.1.17
Model parameters
We simulated genetic profiles and disease status for 100,000 subjects. For each combination of the model parameters (allele frequency, ORs and disease prevalence), we considered genetic profiles that were defined by 1–400 genes. For genetic profiles with more than 50 genes, we calculated the AUC for every 10 genes added (i.e., genetic profiles defined by 50, 60 400 genes). In the first series, we assumed constant ORs for the heterozygous risk genotypes and considered ORs ranging from 1.05–2.0 in separate simulations. In the second series, we constructed genetic profiles with genes that had ORs ranging from 1.05–3.0 and risk allele frequencies ranging from 5–30%. The relationship of the AUC and the proportion of variance explained by genetic factors were examined for prevalence of disease of 1%, 10% and 30%. Unlike the AUC, the proportion of explained variance is known to vary with the disease prevalence.11
RESULTS
We first examined the discriminative accuracy of genetic profiling as a function of the number of genes involved assuming that all genes had the same risk allele frequency and the same ORs for the genotypes. Figure 2 shows that the discriminative accuracy of genetic profiling was higher when more genes were involved, but the flattening of the curves shows that each additional gene had a smaller contribution to the AUC. As expected, the discriminative accuracy was higher when the individual genes were stronger predictors of disease, as indicated by the magnitude of the ORs (Fig. 2), and when the risk alleles were more common (Table 2). The AUC of genetic profiling based on 400 genes with an allele frequency of 10% exceeded 0.80 when the ORs of the heterozygous genotypes were 1.25 or 1.5. This level of discrimination was not reached when only genes with weak effects (OR = 1.10 or 1.05) were modeled to be involved (Fig. 2). Even when the risk alleles were more common than 10%, the AUC of profiles consisting of 400 genes with effects of 1.05 or 1.10 did not reach an AUC of 0.80 (Table 2).
Discriminative accuracy of genetic profiling as a function of the number of genes involved in the disease. Each smoothed line presents the areas under the receiver-operating characteristic curves of 400 simulations in which genetic profiles were based on 1–400 genes with equal odds ratios (ORs) for the genotypes. The number next to each line presents the magnitude of the OR for the heterozygous genotype, with the OR for the homozygous risk genotype being the square of this OR. The allele frequency was 10% for all risk alleles and the disease prevalence was 10%. AUC, area under the receiver-operating characteristic curve.
Second, we evaluated genetic profiles defined by genes that had different effects on the disease. We considered a small number of genes with relatively rare mutations that are strongly associated with the disease and many genes with common mutations that are associated with minor increases in disease risk (Figs 3A,B). We investigated three scenarios that differed in the ORs of the 20 strongest genes (Fig. 3A) with the most predictive gene having an OR of 1.5, 2.0 and 3.0 for the heterozygous genotype. The differences between the curves in Figure 3C show that the discriminative accuracy of genetic profiling was markedly improved when at least a few strong genetic predictors were involved. The figure demonstrates that an AUC of 0.80 could also be obtained when only the strongest heterozygous genotype was associated with a 1.5-fold increase in risk of disease.
Discriminative accuracy of genetic profiling based on genes with varying odds ratios and risk allele frequencies. (A) Distributions of the odds ratios (ORs) for the heterozygous risk genotypes of the 400 genes that are that are considered in the three scenarios. The scenarios differ in the ORs of the 20 strongest genes, whereas the ORs for the other genes decrease from 1.15 to 1.05. The ORs of the strongest gene range from 1.5–1.15 in scenario 1, from 2.0–1.15 in scenario 2 and from 3.0–1.15 in scenario 3. (B) The corresponding allele frequencies of the 400 genes: The strongest gene in each scenario has an allele frequency of 0.05, the second of 0.055, and so on. Hence, we assume in these scenarios that genotypes with higher ORs are infrequent and genotypes with lower ORs are common. (C) The areas under the receiver-operating characteristic curves (AUCs) for the genetic profiles that are based on 1–400 genes. The numbers next to the lines (C) refer to the highest OR of the distributions (A).
Finally, we investigated the AUC in relation to the proportion of variance explained by genetic factors, which is a summary measure of the total contribution of genetic factors involved in the onset of disease. Because we assumed that the genetic profiles were based on all genes involved, this proportion of explained variance can be viewed of as an estimate of the heritability. Hence, the associated AUC indicates the maximum discriminative accuracy that can be obtained by genetic profiling for a disease given its heritability. Figure 4 shows the curvilinear relationship between the AUC and the proportion of explained variance for diseases with a prevalence of 1%, 10% and 30%. As expected, we found that the higher the contribution of genetic factors, the higher the AUC. For each value of the proportion of explained variance, rare diseases reached higher AUCs than common diseases. For example, when the proportion of explained variance was 0.30, the maximum AUC was 0.83 when the disease prevalence was 30% and 0.97 when the disease prevalence was 1%. Note that these values are not merely determined by the strength of the risks associated to the single genotypes: it does not make a difference whether this proportion of explained variance is determined by a small number of genes with a strong effect or a large number of weak genetic predictors.
DISCUSSION
We quantified the clinical usefulness of genetic profiling as its accuracy in discriminating between subjects who will develop the disease and those who will not. The results of our simulation study demonstrate that a high (AUC > 0.80) to excellent discriminative accuracy (AUC > 0.95) can be obtained by genetic profiling using genes with only a small effect individually. The discriminative accuracy depends, as expected, on the number of genes involved, the frequency of the risk alleles and the risks associated with the genotypes. A higher discriminative accuracy can be obtained when genetic factors play a larger role in the disease, as indicated by the proportion of explained variance. It is irrelevant whether a few rare but strong genetic predictors or a large number of common susceptibility genes are involved.
As for most diseases the large majority of genes remain to be identified, we had to make assumptions of the effect of genes underlying complex diseases. Our results are valid conditional on the following three assumptions. First, as others, we assumed a multiplicative model to calculate the probability of disease for the genetic profiles.14,15 Under the assumption of an additive risk model, the standard deviations of the probability distributions will be reduced, which may reduce the discriminative accuracy of the genetic profiling. Second, we did not consider epistatic effects in this paper as there is an infinite number of ways through which genes may interact when studying hundreds of genes. Gene-gene and gene-environment interactions may further improve the discriminative accuracy of genetic profiling – toward the maximum value that is predicted based on the heritability and disease prevalence (Fig. 4). Observational data will be needed to meaningfully examine the contribution of these interaction effects to the usefulness of genetic profiling. Third, we considered up to 400 genes for which the ORs of the heterozygous genotypes were as low as 1.05 (Figs 2 and 3). We assumed that we had included all genes involved in the disease, that genes with low ORs (≤1.05) could be identified and that all effects could be quantified reliably. However, the quantification of such low-risks may require large epidemiological studies, which will not be readily available in the near future. Furthermore, it is argued that a substantial proportion of the genetic variance involves rare variants and gene-gene and gene-environment interactions that are not easily identifiable. Hence, the possibilities for presymptomatic genetic testing may eventually be limited by our capacity to identify and quantify low-risk genes and rare variants.
When interpreting the implications of our findings, it is important to realize that the level of discrimination that is required in clinical care and public health applications depends, among other things, on the goal of testing, the burden of disease, the costs of disease, the availability of (preventive) treatment and the adverse effects of false-positive and false-negative test results. Screening programs, which aim to identify high-risk groups, typically have AUCs ∼ 0.80.7,8 At this level of discriminative accuracy, however, there is still a considerable number of subjects who will test positive but will not develop the disease, or test negative and will develop the disease. When the medical, financial and psychological costs of both false-positive and false-negative results are too high, e.g., decreased survival among false-negatives through the late detection of cancer and increased screening participation and worries among the large group of false-positives, the discriminative accuracy needs to be much higher. Our simulation studies show that high discriminative accuracy was obtained when the genetic profiles at least included a few common genes that were strong predictors of disease either by themselves. This leads to the conclusion that for most complex disorders genetic profiling may become possible for the identification of high-risk groups in screening programs, but will only qualify for presymptomatic diagnosis of rare complex diseases with a high heritability. This conclusion is similar to that of Yang et al., who recently investigated the number of genes that underlie the occurrence of common complex diseases.18 They found that a few genes with common risk variants could explain a major proportion of common complex diseases in the population. These conclusions may seem in contrast to previous studies that doubted the public health benefits of testing low-risk susceptibility genes.3,4 However, both Vineis et al. and Holtzman and Marteau quantified the usefulness of genetic testing for a single susceptibility gene. This paper and that of Yang et al. show that the simultaneous testing of multiple low-risk genes can have public health relevance.
We demonstrated that the maximum discriminative accuracy of genetic profiling can be deduced from the heritability and prevalence of disease. Figure 4 shows that excellent discrimination (AUC > 0.95) may become a realistic scenario for diseases with a prevalence of 1%, when the proportion of variance explained by genetic factors is ≥0.23 or higher, but less realistic for diseases with a prevalence of 30%, unless the proportion of explained variance is >0.63. High levels of heritability have been reported for Alzheimer's disease and osteoporosis,19,20 but are unlikely for common cardio- and cerebrovascular diseases for which the heritability is more likely to be lower than 50%.21 Note that for a given heritability the discriminative accuracy is higher for rare diseases. This is explained by the fact that AUC is independent of disease prevalence, while the proportion of explained variance (heritability) does depend on the prevalence of disease. Furthermore, AUC is a measure of discrimination, whereas heritability refers to the proportion of explained variance by genetic factors. For rare diseases a higher AUC can be obtained with a lower heritability, but this may not necessarily mean that the positive predictive values associated with the genetic profiles are also higher compared to common diseases with the same heritability. It is recommended that further studies also include other indicators of the usefulness of genetic profiling such as the positive predictive value, population-attributable fraction and number needed to treat.
Perhaps the most important conclusion of our paper is that based on the relationship between heritability and AUC we are able to predict whether testing by genetic profiling may be feasible, even if we have not yet identified the genes that are involved.
References
Collins FS, McKusick VA . Implications of the Human Genome Project for medical science. JAMA 2001; 285: 540–544.
Valle D . Genetics, individuality, and medicine in the 21st century. Am J Hum Genet 2004; 74: 374–381.
Vineis P, Schulte P, McMichael AJ . Misconceptions about the use of genetic tests in populations. Lancet 2001; 357: 709–712.
Holtzman NA, Marteau TM . Will genetics revolutionize medicine?. N Engl J Med 2000; 343: 141–144.
Janssens ACJW, Pardo MC, Steyerberg EW, Van Duijn CM . Revisiting the clinical validity of multiplex genetic testing in complex diseases. Am J Hum Genet 2004; 74: 585–588.
Yang Q, Khoury MJ, Botto L, Friedman JM . Revisiting the clinical validity of multiplex genetic testing in complex diseases: reply to Janssens etal. Am J Hum Genet 2004; 74: 588–589.
Wilson PW, D'Agostino RB, Levy D, Belanger AM . Prediction of coronary heart disease using risk factor categories. Circulation 1998; 97: 1837–1847.
Chen P, Ratcliff G, Belle SH, Cauley JA . Cognitive tests that best discriminate between presymptomatic AD and those who remain nondemented. Neurology 2000; 55: 1847–1853.
Rudan I, Smolej-Narancic N, Campbell H, Carothers A . Inbreeding and the genetic complexity of human hypertension. Genetics 2003; 163: 1011–1021.
Hanley JA, McNeil BJ . The meaning and use of the area under a receiver-operating characteristic (ROC) curve. Radiology 1982; 143: 29–36.
Ash A, Shwartz M . R2: a useful measure of model performance when predicting a dichotomous outcome. Stat Med 1999; 18: 375–384.
Snyder EE, Walts B, Perusse L, Chagnon YC . The human obesity gene map: The 2003 update. Obes Res 2004; 12: 369–439.
Sackett DL, Haynes RB, Tugwell P . Clinical epidemiology: a basic science for clinical medicine. Boston/Toronto: Little, Brown and Company; 1985.
Pharoah PD, Antoniou A, Bobrow M, Zimmern RL . Polygenic susceptibility to breast cancer and implications for prevention. Nat Genet 2002; 31: 33–36.
Peto J . Breast cancer susceptibility-A new look at an old model. Cancer Cell 2002; 1: 411–412.
Harrell FE . Design and Hmisc R function library. Available at: http://biostat.mc.vanderbilt.edu/twiki/bin/view/Main/RS. Accessed February, 2006.
R Development Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria 2004. Available at: http://www.R-project.org. Accessed May 1, 2004.
Yang Q, Khoury MJ, Friedman JM, Little J . How many genes underlie the occurrence of common complex diseases in the population?. Int J Epidemiol 2005.
Pedersen NL, Posner SF, Gatz M . Multiple-threshold models for genetic influences on age of onset for Alzheimer disease: findings in Swedish twins. Am J Med Genet 2001; 105: 724–728.
Peacock M, Turner CH, Econs MJ, Foroud T . Genetics of osteoporosis. Endocr Rev 2002; 23: 303–326.
Fox CS, Polak JF, Chazaro I, Cupples A . Genetic and environmental contributions to atherosclerosis phenotypes in men and women: Heritability of carotid intima-media thickness in the Framingham Heart Study. Stroke 2003; 34: 397–401.
Acknowledgements
The study was financially supported by the Netherlands Organization for Scientific Research (NWO pioneer and ZonMW; grant number 945-10-039) and the Center for Medical Systems Biology (CMSB).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Janssens, A., Aulchenko, Y., Elefante, S. et al. Predictive testing for complex diseases using multiple genes: Fact or fiction?. Genet Med 8, 395–400 (2006). https://doi.org/10.1097/01.gim.0000229689.18263.f4
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1097/01.gim.0000229689.18263.f4
Keywords
This article is cited by
-
Interplay of the Mediterranean diet and genetic hypertension risk on blood pressure in European adolescents: Findings from the HELENA study
European Journal of Pediatrics (2024)
-
Development of a genetic risk score for obesity predisposition evaluation
Molecular Genetics and Genomics (2022)
-
The clinical utility of polygenic risk scores for chronic lymphocytic leukemia
Leukemia (2021)
-
Development of a Genetic Risk Score to predict the risk of overweight and obesity in European adolescents from the HELENA study
Scientific Reports (2021)
-
Detection of gene-environment interactions in the presence of linkage disequilibrium and noise by using genetic risk scores with internal weights from elastic net regression
BMC Genetics (2017)