Main

As pinch-off is approached, the length and timescales near the singularity become much smaller than the scale of the initial conditions that caused the singularity to form. In this regime the interfacial morphology can be written in scale-independent self-similar coordinates2. Experimental investigations of self-similar evolution that determine both the interfacial morphology and dynamics near topological singularities have largely been confined to multiphase fluids. In some cases, the interface asymptotically approaches a symmetric cone shape as the time of pinch-off is approached. For pinching by surface diffusion, a countable set of solutions can be identified, each with a different cone angle. A stable solution is found for only the largest cone angle, and thus the geometry of the system close to pinching is universal12. This universality has not been observed experimentally. There is no corresponding analysis for pinching through mass diffusion in the bulk phases.

We examine the evolution of interfacial morphology of liquid rods in a solid matrix. An Al–15 wt.% Cu alloy is employed along with 4D synchrotron radiation-based tomographic microscopy. The interfaces evolve by bulk diffusion of solute through the high-diffusivity liquid21. The rods were created by holding a 1-mm-diameter sample isothermally 5 °C above the eutectic temperature to form a solid–liquid mixture. The interfacial morphology of liquid rods was observed in situ using tomographic microscopy at the TOMCAT beamline of the Swiss Light Source over a 12 h period22,23 (see Methods for details). Hundreds of pinching events were observed during this time. Figure 1 shows one such pinching event.

Figure 1: Time sequence of a liquid rod pinching owing to interfacial-energy-driven bulk diffusion.
figure 1

a, 142.5 min; b, 155 min; c, 165 min; d, 170 min.

Full size image

To determine whether a self-similar solution exists near pinch-off, we define a set of self-similar variables in cylindrical coordinates:

where r is the radial coordinate of the interface position, t is time, z is the axial coordinate, ts is the time of the singularity, η and ξ are the radial and axial coordinates in the time-independent similarity variables, B is a scaling constant dependent on material properties and α is an exponent specific to the process. The system is assumed to be symmetric about the z and ξ axes.

We assume that the diffusion coefficient of solute in the solid, DS=0 in the surrounding solid, and that interface motion is slow compared with the time required for the diffusion field to relax. Thus the diffusion field in the liquid is given by a solution to Laplace’s equation:

where CL is the solute concentration in the liquid. We seek a solution to (2) consistent with the boundary conditions. The first is the Gibbs–Thomson equation

where CL is the solute concentration on the liquid side of the interface, CL0 and CS0 are the equilibrium solute concentrations at a flat interface, d0 is the capillary length and H is the mean interfacial curvature. The other boundary condition is the interfacial mass balance,

where v is the interfacial velocity in the direction normal to the interface, DL is the diffusion coefficient in liquid and ∂ CL/∂ n is the derivative of the concentration field in the normal direction.

We seek a similarity solution to (2) consistent with the boundary conditions by defining the difference between the solute concentration in the liquid and the equilibrium concentration in terms of a scaled concentration in similarity variables, K(ξ,η):

where A is a scaling constant dependent on materials properties. Substituting (5) into (3) and (4) and using (1), we find that α=−β=1/3 is required for a self-similar solution consistent with the boundary conditions and Laplace’s equation. From (3) and (4), a similarity solution also requires that B=(DLd0)−1/3 and A=(CL0−CS0)(d02/DL)1/3. The interfacial coordinates thus scale as r∼z∼[DLd0(ts−t)]1/3.

If the pinching process is self-similar, the diameter of the rod should decrease as (t−ts)1/3. Using data such as those shown in Fig. 1, we can determine whether this is the case in the experiment. As the data are obtained in three dimensions, it is possible to view the rod along its axis to measure accurately its smallest cross-section or diameter. Figure 2 shows that the diameter decreases linearly as (t−ts)1/3 for a single pinching rod. This behaviour was also observed in the 19 other pinching events investigated. These data suggest the presence of self-similar interfacial evolution, and we thus proceed to examine theoretically the interfacial morphology near the topological singularity.

Figure 2: Rod diameter follows a power law before singularity.
figure 2

The diameter of a single pinching rod as a function of (t−ts)1/3 along with the experimentally measured and theoretically predicted interface shapes at various times and a line showing the least-squares fit to the experimental data. Error bars show the standard deviation in the measured diameters of the single rod, which is not circular at all times. Experimental error in each measurement is one half-voxel in size or 0.74 μm. It is clear that, even when the interfacial morphology is far from the self-similar shape, the kinetics of the pinching process are still well described by (t−ts)1/3.

Full size image

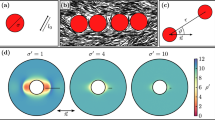
Using the similarity variables of (1), the interfacial morphology, both before and after pinching, was determined numerically using a boundary-integral method (see Methods for details). The solid–liquid interface position is given by the function η=f(ξ), along which K(ξ,η) is equal to the interfacial curvature. After pinch-off, solutions were found for the shape of the two receding tips at any cone angle, consistent with previous findings for the pinch-off of rods by surface diffusion10. Before pinch-off, we find a discrete set of solutions for various cone angles, where the cone angle is defined as twice the angle of the interface from the ξ axis as . For diffusion inside the rod, we find solutions for cone angles of 30° and 76°; see Fig. 3. Further solutions are expected at cone angles smaller than 30°. However, as in the surface-diffusion-limited case12, we expect that only the solution with the largest cone angle is stable and thus observable experimentally.

Figure 3: Theoretically predicted interface shapes before the singularity.
figure 3

a, Diffusion inside the rod. b, Diffusion in the matrix outside the rod. Axes and interfaces are in the self-similar coordinates of equation (1). The shapes approach a cone with angle 76°, solid line, and 30°, dashed line (a), and 80° (b), far from the singularity at ξ=0.

Full size image

Additionally, we find that, for pinching by bulk diffusion outside the rod, the stable solution has a cone angle of 80° (with unstable solutions also expected but not identified). Examples where this shape would be found include the pinch-off of solid rods surrounded by liquid in Al–Cu at lower volume fractions of solid24 and the pinching of atomically ordered eutectic intermetallic rods embedded in an atomically disordered intermetallic matrix25.

The similarity solution for the interface shape η=f(ξ) determines the prefactor of the temporal power law of the pinching event. Using (1), the radius at the centre (ξ=0) of a pinching liquid rod, R(t), evolves as

where f(0)=0.60 and 0.37 for the solutions with cone angles of 76°, and 30°, respectively; see Fig. 3. Thus, sufficiently close to the singularity, the time dependence of the radius is independent of initial conditions and is a function of only f(0) and materials parameters.

Theory thus suggests that, as the topological singularity is approached, the interfacial shape may be universal; it does not depend on the initial conditions of the rod and materials system, and the kinetics of the pinching process are described by a simple temporal power law. This unique solution will also determine the shape before and after the pinching event. However, two issues remain to be addressed before we can conclude that the pinching process is universal: most importantly, whether the quasistationary approximation will hold sufficiently close to the pinch-off for universality to be observed, and second, whether there is evidence for similarity shapes with cone angles other than 76°.

To assess the validity of the quasistationary approximation, we define the characteristic length scale l as the diameter of the pinching rod, and the characteristic timescale τ as

Writing the diffusion equation in dimensionless form after scaling by these characteristic length and timescales, we obtain

where is the dimensionless time, c is concentration, is the dimensionless Laplacian and ε=[2f(0)]3d0/l. The quasistationary approximation is valid as long as ε≪1. Using f(0)=0.60 and the capillary length for the solid–liquid interface in Al–Cu, d0=2.27 nm (ref. 27), the quasistationary approximation holds as long as the rod diameter is much greater than 3.9 nm, well below the 1.48 μm resolution of the tomography.

We test the theory by comparing the kinetics predicted by the similarity solution with experimental data on the evolution of rod diameter. From (6), the slope of the line shown in Fig. 2 is related to the materials parameters and f(0), the interface location in similarity variables at ξ=0. Linear slopes were determined for 19 pinching events on the basis of diameters measured for at least three time steps before ts. The average slope was 1.35 μm s−1/3 with a standard deviation of 0.211 μm s−1/3. From (6), the predicted slope, or prefactor, is given by 2f(0)(DLd0)1/3 (the factor of two converts radius to diameter). Using DL=8.3×10−10 m2 s−1 (ref. 26), d0=2.27 nm (ref. 27) and f(0)=0.60, the theoretically predicted prefactor is 1.47 μm s−1/3. This is within 0.57σ of the experimentally measured prefactor, indicating an excellent agreement between theory and experiment, given the uncertainties in the materials parameters. If we had used, instead, f(0) for the solution with a cone angle of 30°, the predicted prefactor would be 0.91 μm s−1/3, or 2.1σ below the value measured experimentally. Any other possible solutions will have cone angle smaller than 30° and a smaller f(0) (ref. 12), so the predicted prefactor would be even smaller. This suggests that only the solution with a cone angle of 76° is observable experimentally. Moreover, the agreement between theory and experiment is excellent from very early in the pinching process.

As a further test of the theory, a three-dimensional representation of the theoretically predicted interface shape was created. We aligned the experimental data to the theoretically predicted shape for the solution with a cone angle of 76°, and linearly scaled the predicted shape such that the diameter at the centre of the pinching rod was the same as that measured experimentally (see Methods for details). The distance from the theoretically predicted shape to the closest point on the experimentally measured shape was calculated; see Fig. 4. As expected, the agreement between theory and experiment improved as the singularity is approached, because initial conditions have less influence and the shape becomes locally determined. Just before pinch-off, the mean deviation between shapes is less than the 1.48 μm resolution of the X-ray tomographic microscopy scan, indicating excellent agreement between theory and experiment. Even in the region where the experimentally measured shape differs most from the theory (lower right of Fig. 4d), the measured cone angle is 66°–71° (using the experimental error of 0.74 μm). Very similar diagrams result if we plot the distance between the experimentally measured and theoretically predicted shapes in similarity variables, confirming that the improved agreement as ts is approached is not just a result of the changing length scale. In some cases, the initial shapes of the rods were asymmetric about the pinching axis, but still decayed at the rate predicted by the symmetric solution. In all 19 cases examined the agreement between theory and experiment improved as the singularity was approached. Thus, to the resolution of the tomography, the experiments confirm that, some distance from the pinching point, the shape approaches a cone with the predicted cone angle of 76°.

Figure 4: Quantifying agreement between theoretically predicted and experimentally measured interface shapes.
figure 4

Top, the experimentally determined microstructure is superimposed on the theoretically predicted shape for the solution with a cone angle of 76° for several times leading up to pinch-off. The theoretical shapes are scaled to the same diameter as the experimental microstructures. Bottom, the theoretical shape is shown coloured by the distance from each point to the closest point on the experimentally measured shape. The mean deviation between experiment and theory decreases as the system approaches the time of pinch-off. In the case of the final time step, the mean deviation is less than the experimental resolution of the X-ray tomographic microscopy scan (1.48 μm). a, 85 min; b, 142.5 min; c, 180 min; d, 190 min.

Full size image

Both the interfacial morphology and dynamics of the pinching process measured experimentally agree with the predictions of theory for the solution with a cone angle of 76°, implying that the shape with the highest cone angle is the only stable shape. We therefore conclude that the pinching process under interfacial-energy-driven bulk diffusion is governed by a unique self-similar solution.

We find that topological singularities in a system evolving by a previously unexplored class of dynamics exhibit universal behaviour. Furthermore, the dynamics of the pinching process by capillarity-induced bulk diffusion agree very well with those predicted theoretically, even early in the pinching process, when the interfacial morphology is not precisely that given by theory. The theory also shows that self-similar shapes exist when pinching occurs by diffusion outside the rod, and we conjecture that the shape with the largest cone angle is also universal. As the prefactor of the temporal power law is in agreement with theory from very early in the evolution of the morphological instability, the universal behaviour caused by the approaching singularity exhibits itself far before the singularity occurs. These results are applicable to a variety of systems that exhibit topological singularities, such as eutectic and bicontinuous two-phase mixtures, and could be used, for example, to calculate the time required for a non-symmetric bicontinuous mixture to lose continuity in one phase, which results in a dramatic change in properties of the material.

Methods

Numerical solution for shape.

We seek a solution for the shape of the solid–liquid interface in similarity variables, η=f(ξ), or defined parametrically F=η−f(ξ)=0, assuming axial symmetry about ξ. Laplace’s equation and the boundary conditions (3), (4) were transformed into the self-similar coordinate system. Green’s third identity was used along with the free-space Green’s function for Laplace’s equation to yield an integrodifferential equation for the scaled concentration K(ξ,η) on the interface:

where g is the free-space Green’s function for Laplace’s equation, g=1/|r(ξ0,η0)−ri(ξ,η)|, n is the unit normal vector to the interface and r(ξ0,η0) and ri(ξ,η) are the field and source points, respectively. On the boundary, the concentration difference from equilibrium can be written in terms of the Gibbs–Thomson condition in similarity variables

because . The solute-conservation boundary condition can used in combination with the material derivative for the interface to find ∂ K/∂ n on the boundary

where the subscripts denote partial differentation. Substituting (8) and (9) into (7) gives a set of integrodifferential equations for f(ξ). Boundary conditions on f(ξ) are that f(ξ) approaches a straight line with angle θc/2 (where θc is the cone angle) from the ξ axis as and f′(0)=0, which ensures finite curvature at the origin.

The integrodifferential equations were discretized, and the angular integral was rewritten as a complete elliptic integral of the first kind and approximated using the polynomial approximation of ref. 28. The integration was carried out numerically using the trapezoidal rule on a truncated domain along ξ. A Taylor expansion was used to approximate integrable singularities when ξ=ξ0. Newton’s method was then used to iteratively solve for f(ξ). A coarse grid spacing along ξ was used to search for solutions as θc was varied. The grid spacing was refined using solutions from the coarse mesh as an initial guess to narrow down the exact cone half-angle to ±1°. Convergence was tested by varying the grid spacing and by varying truncation length in the ξ-direction; second-order convergence was obtained.

Experiment.

Al–15 wt% Cu was directionally solidified to form Al-rich dendrites. In preparation for X-ray tomographic microscopy, 1-mm-diameter samples were cut from the original ingot and mounted in a custom-made sample furnace. The samples were coarsened in situ at 565 °C, and data were collected in real time using X-ray tomographic microscopy at the TOMCAT beamline located at the X02DA port of the Swiss Light Source at the Paul Scherrer Institut (Villigen, Switzerland). An energy of 20 keV was used with 80 ms exposure time, and 721 projections were captured over the 180° of rotation. A total of 1,024 slices, with a spatial resolution of 1.48 μm3 per voxel, were collected at 150 s intervals for the first 4.5 h and at 450 s for the remaining 7.5 h. The tomograms were then converted to binary using sample-specific algorithms created in the IDL software package. Further information about the TOMCAT beamline and the details of the experiment can be found in refs 22 and 23, respectively.

Data analysis.

In preparation for analysis, three-dimensional arrays from the experiment were smoothed to remove alignment and reconstruction artefacts from the interface. The arrays were then imported into the visualization program Amira, and the arrays were cropped to an individual pinching event. The pinch-off diameters (that is, the minimum diameters at the centre) were measured using Amira. The theoretically predicted shape was also imported into Amira and the principal (or longitudinal) axes of the experimental shapes were then aligned with the theoretically predicted shape by aligning the two shapes to the axes with the lowest moment of inertia.

The pinch-offs at each time-step were scaled such that the cone diameter matched that of the theoretical shape. Scaling the pinch-offs to the theoretical shape provided a way to quantitatively observe the self-similarity and interface agreement with the theory over time. By plotting the diameter cubed versus time, the critical pinching time, ts, was measured on the basis of a linear fit. The deviation between theory and experiment at a given vertex was determined as the distance to the closest point on the other surface.