Network structure and dynamics
Machine learning meets complex networks via coalescent embedding in the hyperbolic space
Alessandro Muscoloni et al., Nat. Commun. 8 1615 (2017)
 Mapping complex networks to underlying geometric spaces can help understand the structure of networked systems. Here the authors propose a class of machine-learning algorithms for efficient embedding of large real networks to the hyperbolic space, with potential impact on big network-data analysis.
Mapping complex networks to underlying geometric spaces can help understand the structure of networked systems. Here the authors propose a class of machine-learning algorithms for efficient embedding of large real networks to the hyperbolic space, with potential impact on big network-data analysis.
Dynamic patterns of information flow in complex networks
Uzi Harush and Baruch Barzel, Nat. Commun. 8 2181 (2017)
 Complex networks are a useful tool to investigate disease spreading and social networks, but topology alone is insufficient to predict information flow. Here the authors propose a measure of information flow and predict its behaviour from the interplay between structure and dynamics.
Complex networks are a useful tool to investigate disease spreading and social networks, but topology alone is insufficient to predict information flow. Here the authors propose a measure of information flow and predict its behaviour from the interplay between structure and dynamics.
Modelling sequences and temporal networks with dynamic community structures
Tiago P. Peixoto and Martin Rosvall, Nat. Commun. 8 582 (2017)
 The description of temporal networks is usually simplified in terms of their dynamic community structures, whose identification however relies on a priori assumptions. Here the authors present a data-driven method that determines relevant timescales for the dynamics and uses it to identify communities.
The description of temporal networks is usually simplified in terms of their dynamic community structures, whose identification however relies on a priori assumptions. Here the authors present a data-driven method that determines relevant timescales for the dynamics and uses it to identify communities.
The diverse club
Maxwell A. Bertolero et al., Nat. Commun. 8 1277 (2017)
 Complex networks represent systems such as neural networks and air traffic as interconnected nodes that organize themselves into subsets. Here Bertolero et al. propose a subset which they call the diverse club, which offers an alternative to the commonly used rich club and whose members are well placed to support global integration in complex networks.
Complex networks represent systems such as neural networks and air traffic as interconnected nodes that organize themselves into subsets. Here Bertolero et al. propose a subset which they call the diverse club, which offers an alternative to the commonly used rich club and whose members are well placed to support global integration in complex networks.
The topological requirements for robust perfect adaptation in networks of any size
Robyn P. Araujo and Lance A. Liotta, Nat. Commun. 9 1757 (2018)
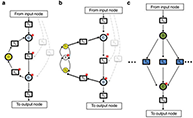 Robust perfect adaptation (RPA), the ability of a system to return to its pre-stimulus state in presence of the signal, enables organisms to respond to further changes in stimuli. Here, the authors identify the full set of network module topologies that can confer RPA on complex networks.
Robust perfect adaptation (RPA), the ability of a system to return to its pre-stimulus state in presence of the signal, enables organisms to respond to further changes in stimuli. Here, the authors identify the full set of network module topologies that can confer RPA on complex networks.
Model-free inference of direct network interactions from nonlinear collective dynamics
Jose Casadiego et al., Nat. Commun. 8 2192 (2017)
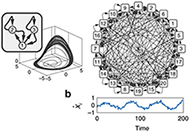 Network dynamical systems can represent the interactions involved in the collective dynamics of gene regulatory networks or metabolic circuits. Here Casadiego et al. present a method for inferring these types of interactions directly from observed time series without relying on their model.
Network dynamical systems can represent the interactions involved in the collective dynamics of gene regulatory networks or metabolic circuits. Here Casadiego et al. present a method for inferring these types of interactions directly from observed time series without relying on their model.
The geometric nature of weights in real complex networks
Antoine Allard et al., Nat. Commun. 8 14103 (2017)
Complex networks have been conjectured to be hidden in metric spaces, where distances between nodes encode their likelihood of being connected – offering a geometric interpretation to networks’ topologies. Here the authors extend this concept to weighted networks, providing empirical evidence on the metric natures of weights. Presenting a general class of weighted networks embedded in hidden metric spaces that reproduces many properties of real networks, the authors can explore whether the origin of a networks’ topology and their weighs emerges from the same dynamics.
Articulation points in complex networks
Liang Tian et al., Nat. Commun. 8 14223 (2017)
 Given a network, the removal of an articulation point disconnects it; therefore, such nodes play an important role in establishing networks' robustness or connectivity. Here the authors develop analytical tools to characterize articulation points in arbitrary networks, estimating their expected number and a network’s vulnerability to their removal. On this basis, the authors propose an articulation-point-targeted network attack strategy and a network decomposition method.
Given a network, the removal of an articulation point disconnects it; therefore, such nodes play an important role in establishing networks' robustness or connectivity. Here the authors develop analytical tools to characterize articulation points in arbitrary networks, estimating their expected number and a network’s vulnerability to their removal. On this basis, the authors propose an articulation-point-targeted network attack strategy and a network decomposition method.
Quantification of network structural dissimilarities
Tiago A. Schieber et al., Nat. Commun. 8 13298 (2017)
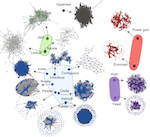 Identifying and quantifying dissimilarities among graphs is a problem of practical importance, but current approaches are either limited or computationally demanding. Here, the authors propose an efficiently computable measure for network comparison that is based on quantifying differences between probability distribution extracted from network pairs. Through extensive computational experiments on real-world graphs, the authors demonstrate that their measure is able to identify and quantify structural topological differences that impact information flow.
Identifying and quantifying dissimilarities among graphs is a problem of practical importance, but current approaches are either limited or computationally demanding. Here, the authors propose an efficiently computable measure for network comparison that is based on quantifying differences between probability distribution extracted from network pairs. Through extensive computational experiments on real-world graphs, the authors demonstrate that their measure is able to identify and quantify structural topological differences that impact information flow.
Structure and inference in annotated networks
Mark E. J. Newman and Aaron Clauset, Nat. Commun. 7 11863 (2016)
 Methods used to analyze network structure consider the connections in the network, but usually ignore additional information about the nodes such as gender or age of individuals in social networks. Here, the authors devise an approach that incorporates such metadata when it improves the detection of network communities and ignores it otherwise.
Methods used to analyze network structure consider the connections in the network, but usually ignore additional information about the nodes such as gender or age of individuals in social networks. Here, the authors devise an approach that incorporates such metadata when it improves the detection of network communities and ignores it otherwise.
Emergence of core–peripheries in networks
Trivik Verma et al., Nat. Commun. 7 10441 (2016)
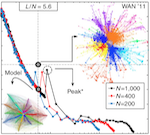 Many real-world transport networks exhibit a core-periphery structure, where few nodes are highly interconnected and the rest form a tree-shaped structure. Understanding how such structure emerges remains unclear. Here the authors demonstrate that a pruning process applied to a fully connected network where underutilized edges are cut and loads are re-distributed can lead to a core-periphery arrangement.
Many real-world transport networks exhibit a core-periphery structure, where few nodes are highly interconnected and the rest form a tree-shaped structure. Understanding how such structure emerges remains unclear. Here the authors demonstrate that a pruning process applied to a fully connected network where underutilized edges are cut and loads are re-distributed can lead to a core-periphery arrangement.
Identifying causal gateways and mediators in complex spatio-temporal systems
Jakob Runge et al., Nat. Commun. 6 8502 (2015)
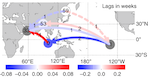 Identifying regions important for spreading and mediating perturbations is crucial to assess the susceptibility of spatio-temporal complex systems. Indeed, events such as volcanic eruption or pollution may have different effects on Earth’s climate system if the region they occur in is strongly globally connected. Here the authors combine dimension reduction, causal reconstruction and causal interaction quantification to re-construct a causally weighted directed network on which it is possible to identify causal pathways and key regions of causal perturbation spread, and apply it to a global atmospheric dataset.
Identifying regions important for spreading and mediating perturbations is crucial to assess the susceptibility of spatio-temporal complex systems. Indeed, events such as volcanic eruption or pollution may have different effects on Earth’s climate system if the region they occur in is strongly globally connected. Here the authors combine dimension reduction, causal reconstruction and causal interaction quantification to re-construct a causally weighted directed network on which it is possible to identify causal pathways and key regions of causal perturbation spread, and apply it to a global atmospheric dataset.