Customize the experiment for the setting instead of adjusting the setting to fit a classical design.
Main
To maximize the chance for success in an experiment, good experimental design is needed. However, the presence of unique constraints may prevent mapping the experimental scenario onto a classical design. In these cases, we can use optimal design: a powerful, general-purpose tool that offers an attractive alternative to classical design and provides a framework within which to obtain high-quality, statistically grounded designs under nonstandard conditions. It can flexibly accommodate constraints, is connected to statistical quantities of interest and often mimics intuitive classical designs.
For example, suppose we wish to test the effects of a drug’s concentration in the range 0–100 ng/ml on the growth of cells. The cells will be grown with the drug in test tubes, arranged on a rack with four shelves. Our goal may be to determine whether the drug has an effect and precisely estimate the effect size or to identify the concentration at which the response is optimal. We will address both by finding designs that are optimal for regression parameter estimation as well as designs optimal for prediction precision.
To illustrate how constraints may influence our design, suppose that the shelves receive different amounts of light, which might lead to systematic variation between shelves. The shelf would therefore be a natural block1. Since we don’t expect such systematic variation within a shelf, the order of tubes on a shelf can be randomized. Furthermore, each shelf can only hold nine test tubes. The experimental design question, then, is: What should be the drug concentration in each of the 36 tubes?
If concentration were a categorical factor, we could compare the mean response at nine concentrations—a traditional randomized complete block design (RCBD)1. However, because concentration is actually continuous, discrete levels unduly limit which concentrations are studied and reduce our ability to detect an effect and estimate the concentration that produces an optimal response. Classical designs, like full factorials or RCBDs, assume an ideal and simple experimental setup, which may be inappropriate for all experimental goals or untenable in the presence of constraints.
Optimal design provides a principled approach to accommodating the entire range of concentrations and making full use of each shelf’s capacity. It can incorporate a variety of constraints such as sample size restrictions (e.g., the lab has a limited supply of test tubes), awkward blocking structures (e.g., shelves have different capacities) or disallowed treatment combinations (e.g., certain combinations of factor levels may be infeasible or otherwise undesirable).
To assist in describing optimal design, let’s review some terminology. The drug is a ‘factor’, and particular concentrations are ‘levels’. A particular combination of factor levels is a ‘treatment’ (with just a single factor, a treatment is simply a factor level) applied to an ‘experimental unit’, which is a test tube. The shelves are ‘blocks’, which are collections of experimental units that are similar in traits (e.g., light level) that might affect the experimental outcome1. The possible set of treatments that could be chosen is the ‘design space’. A ‘run’ is the execution of a single experimental unit, and the ‘sample size’ is the number of runs in the experiment.
Optimal design optimizes a numerical criterion, which typically relates to the variance or other statistically relevant properties of the design, and uses as input the number of runs, the factors and their possible levels, block structure (if any), and a hypothesized form of the relationship between the response and the factors. Two of the most common criteria are the D-criterion and the I-criterion. They are fundamentally different: the D-criterion relates to the variance of factor effects, and the I-criterion addresses the precision of predictions.
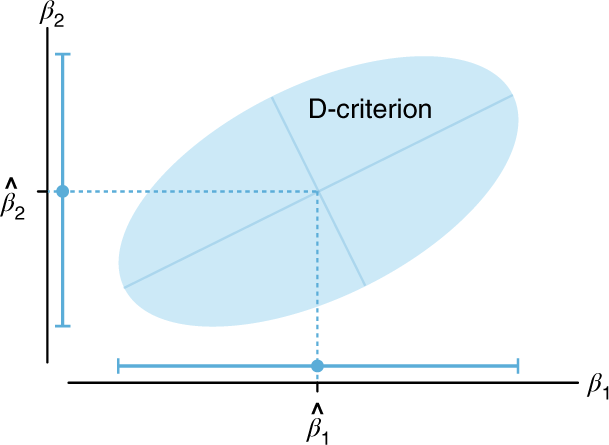
To understand the D-criterion (determinant), suppose we have a quadratic regression model2 with parameters β1 and β2 that relate the factor to the response (for simplicity, ignore β0, the intercept). Our estimates of these parameters, \(\hat \beta _1\) and \(\hat \beta _2\), will have error and, assuming the model error variance is known, the D-optimal design minimizes the area of the ellipse that defines the joint confidence interval for the parameters (Fig. 1). This area will include the true values of both β1 and β2 in 95% (or some other desired proportion) of repeated executions of the design, and its size and shape are a function of the data’s overall variance and the design.
The ellipse can be projected onto each axis to obtain the familiar one-dimensional confidence intervals for each parameter (shown as blue points with error bars). The D-criterion reduces the variance of the parameter estimates and/or the correlation between the estimates by minimizing the area of the ellipse.
On the other hand, the I-criterion (integrated variance) is used when the experimental goal is to make precise predictions of the response, rather than to obtain precise estimates of the model parameters. An I-optimal design chooses the set of runs to minimize the average variance in prediction across the joint range of the factors. The prediction variance is a function of several elements: the data’s overall error variance, the factor levels at which we are predicting, and also the design itself. This criterion is more complicated mathematically because it involves integration.
For both criteria, numerical heuristics are used in the optimization but they do not guarantee a global optimum. For most scenarios, however, near-optimal designs are adequate and not hard to obtain.
Returning to our example, suppose we wish to obtain a precise estimate of our drug’s effect on the mean response. If we expect that the effect is linear (our model has one parameter of interest, β1, which is the slope), the D-optimal design places either four or five experimental units in each block at the low level (0 ng/ml) and the remaining units at the high level (100 ng/ml). Thus, to obtain a precise estimate of β1, we want to place the concentration values as far apart as possible in order to stabilize the estimate. Assigning four or five units of each concentration to each shelf helps to reduce the confounding of drug and shelf effects.
One downside to this simple low–high design is its inability to detect departures from linearity. If we expect that, after accounting for block differences, the relationship between the response and the factor may be curvilinear (with both a linear and quadratic term: y = β0 + β1x + β2x2 + ε, where ε is the error and β0 is the intercept, which we'll ignore here; we also omit the block terms for the sake of simplicity), the D-optimal design is 3–3–3 (at 0, 50 and 100 ng/ml, respectively) within each block.
In many settings, the goal is to learn about whether and how factors affect the response (i.e., whether β1 and/or β2 are non-zero and, if so, how far from zero they are), in which case the D-criterion is a good choice. In other cases, the goal is to find the level of the factors that optimizes the response, in which case a design that produces more precise predictions is better. The I-criterion, which minimizes the average prediction variance across the design region, is a natural choice.
In our example, the I-optimal design for the linear model is equivalent to that generated by the D-criterion: within each block, it allocates either four or five units to the low level and the rest to the high level. However, the I-optimal design for the model that includes both linear and quadratic effects is 2–5–2 within each block; that is, it places two experimental units at the low and high levels of the factor and places five in the center.
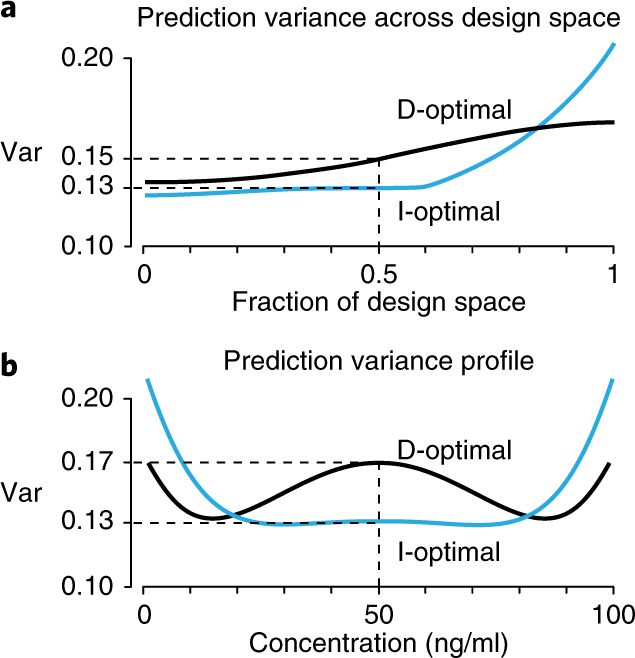
The quality of these designs in terms of their prediction variance can be compared using fraction of design space (FDS) plots3. We show this plot for the D- and I-optimal designs for the quadratic case (Fig. 2a). A point on an FDS plot gives the proportion of the design space (the fraction of the 0–100 ng/ml interval, across the blocks) that has a prediction variance less than or equal to the value on the y axis. For instance, the I-optimal design yields a lower median prediction variance than the D-optimal design: at most 0.13 for 50% of the design space as compared to 0.15. Because of the extra runs at 50 ng/ml, the I-optimal design has a lower prediction variance in the middle of the region than the D-optimal design, but variance is higher near the edges (Fig. 2b).
Our one-factor blocking example demonstrates the basics of optimal design. A more realistic experiment might involve the same blocking structure but three factors—each with a specified range—and a goal to determine how the response is impacted by the factors and their interactions. We want to study the factors in combination; otherwise, any interactions between them will go undetected and the statistical efficiency to estimate factor effects is reduced.
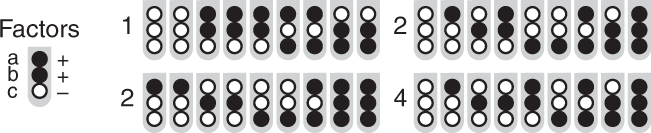
Without the blocking constraint, a typical strategy would be to specify and use a high and low level for each factor and to perform an experiment using several replicates of the 23 = 8 treatment combinations. This is a classical two-level factorial design4 that under reasonable assumptions provides ample power to detect factor effects and two-factor interactions. Unfortunately, this design doesn’t map to our scenario and can’t use the full nine-unit capacity of each shelf—unlike an optimal design, which can (Fig. 3).
The D-optimal design that assigns three factors (a–c) at two levels each—low (unfilled circles) and high (filled circles)—to nine tubes on each of four shelves. The shelves are blocks and the design accounts for the main effects of the three factors and the three two-factor interactions. Each treatment is replicated at least four times, with treatments in tubes 3–7 on each shelf replicated five times.
In unconstrained settings where a classical design would be appropriate, optimal designs often turn out to be the same as their traditional counterparts. For instance, any RCBD1 is both D- and I-optimal. Or, for a design with a sample size of 24, three factors, no blocks, and an assumed model that includes the three factor effects and all of the two-factor interactions, both the D- and I-criteria yield as optimal the two-level full-factorial design with three replicates.
So far, we have described optimal designs conceptually but have not discussed the details of how to construct them or how to analyze them5. Specialized software to construct optimal designs is widely available and accessible. To analyze the designs we’ve discussed—with continuous factors—it is necessary to use regression2 (rather than ANOVA) to meaningfully relate the response to the factors. This approach allows the researcher to identify large main effects or quadratic terms and even two-factor interactions.
Optimal designs are not a panacea. There is no guarantee that (i) the experiment can achieve good power, (ii) the model form is valid and (iii) the criterion reflects the objectives of the experiment. Optimal design requires careful thought about the experiment. However, in an experiment with constraints, these assumptions can usually be specified reasonably.
References
Krzywinski, M. & Altman, N. Nat. Methods 11, 699–700 (2014).
Krzywinski, M. & Altman, N. Nat. Methods 12, 1103–1104 (2015).
Zahran, A., Anderson-Cook, C. M. & Myers, R. H. J. Qual. Tech. 35, 377–386 (2003).
Krzywinski, M. & Altman, N. Nat. Methods 11, 1187–1188 (2014).
Goos, P. & Jones, B. Optimal Design of Experiments: A Case Study Approach (John Wiley & Sons, Chichester, UK, 2011).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Rights and permissions
About this article
Cite this article
Smucker, B., Krzywinski, M. & Altman, N. Optimal experimental design. Nat Methods 15, 559–560 (2018). https://doi.org/10.1038/s41592-018-0083-2
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41592-018-0083-2
This article is cited by
-
Optimal experimental design for precise parameter estimation in competitive cross-reaction equilibria
Journal of the Iranian Chemical Society (2024)
-
Augmented region of interest for untargeted metabolomics mass spectrometry (AriumMS) of multi-platform-based CE-MS and LC-MS data
Analytical and Bioanalytical Chemistry (2023)
-
A microfluidic optimal experimental design platform for forward design of cell-free genetic networks
Nature Communications (2022)
-
Advances, challenges and opportunities in creating data for trustworthy AI
Nature Machine Intelligence (2022)
-
Real-time Adaptive Design Optimization Within Functional MRI Experiments
Computational Brain & Behavior (2020)