Abstract
Electron–positron pair plasmas represent a unique state of matter, whereby there exists an intrinsic and complete symmetry between negatively charged (matter) and positively charged (antimatter) particles. These plasmas play a fundamental role in the dynamics of ultra-massive astrophysical objects and are believed to be associated with the emission of ultra-bright gamma-ray bursts. Despite extensive theoretical modelling, our knowledge of this state of matter is still speculative, owing to the extreme difficulty in recreating neutral matter–antimatter plasmas in the laboratory. Here we show that, by using a compact laser-driven setup, ion-free electron–positron plasmas with unique characteristics can be produced. Their charge neutrality (same amount of matter and antimatter), high-density and small divergence finally open up the possibility of studying electron–positron plasmas in controlled laboratory experiments.
Similar content being viewed by others
Introduction
Electron–positron (e−/e+) plasmas are emitted, in the form of ultra-relativistic winds or collimated jets, by some of the most energetic or powerful objects in the Universe, such as black holes1,2, pulsars3 and quasars4. These plasmas are associated with violent emission of gamma-rays in the form of short-lived (milliseconds up to a few minutes) bursts, which are among the most luminous events ever observed in the Universe. These phenomena represent an unmatched astrophysical laboratory to test physics at its limit and, given their immense distance from Earth (some more distant than several billion light years), they also provide a unique window on the very early stages of our Universe5,6,7. Arguably, one of the most intriguing questions is how these gamma-ray bursts are produced. It is generally accepted that gamma-ray bursts should arise from synchrotron emission of relativistic shocks generated within an electron–positron beam8,9. This radiative mechanism requires a strong and long-lived ( , with ωp being the electron–positron plasma frequency) magnetic field; however, Weibel-mediated shocks generate magnetic fields that should decay on a fast timescale
, with ωp being the electron–positron plasma frequency) magnetic field; however, Weibel-mediated shocks generate magnetic fields that should decay on a fast timescale  due to phase-space mixing9. Also, diffusive Fermi acceleration, a proposed candidate for the acceleration of cosmic rays9, requires magnetic field strengths that are much higher than the average intergalactic magnetic field (≃nT)10. These and other questions could be addressed by ad hoc laboratory experiments; however, the extreme difficulty in generating e−/e+ populations that are dense enough to permit collective behaviour11,12 is still preventing laboratory studies and the properties of this peculiar state of matter are only inferred from the indirect interpretation of its radiative signatures and from matching numerical models. The intrinsic symmetry between negatively charged (e−) and positively charged (e+) particles within the plasma makes their dynamics significantly different from that of an electron-ion plasma or from a purely electronic beam. In the first case, the mass symmetry of the oppositely charged species induces different growth rates for a series of kinetic and fluid instabilities13, and significantly affects the possibility of generating acoustic or drift waves. In the second case, the overall beam neutrality forbids the generation of current-driven magnetic fields that would hamper the onset of transverse instabilities.
due to phase-space mixing9. Also, diffusive Fermi acceleration, a proposed candidate for the acceleration of cosmic rays9, requires magnetic field strengths that are much higher than the average intergalactic magnetic field (≃nT)10. These and other questions could be addressed by ad hoc laboratory experiments; however, the extreme difficulty in generating e−/e+ populations that are dense enough to permit collective behaviour11,12 is still preventing laboratory studies and the properties of this peculiar state of matter are only inferred from the indirect interpretation of its radiative signatures and from matching numerical models. The intrinsic symmetry between negatively charged (e−) and positively charged (e+) particles within the plasma makes their dynamics significantly different from that of an electron-ion plasma or from a purely electronic beam. In the first case, the mass symmetry of the oppositely charged species induces different growth rates for a series of kinetic and fluid instabilities13, and significantly affects the possibility of generating acoustic or drift waves. In the second case, the overall beam neutrality forbids the generation of current-driven magnetic fields that would hamper the onset of transverse instabilities.
Different schemes have been proposed for the laboratory generation of e−/e+ plasmas: in large-scale conventional accelerators, the possibility of recombining high-quality electron and positron beams via magnetic chicanes14 is envisaged and a different approach is foreseen in confining low-energy positrons using radioactive sources with Penning traps11,15. The proposed APEX experiment12 builds on this idea, accumulating a large number of positrons in a multicell Penning trap, before injection into a stellarator plasma confinement device. The major challenge of these schemes is the recombination of these separate electron and positron populations. Alternative schemes have been proposed in which electrons and positrons are generated in situ16,17,18,19,20,21, thus avoiding the aforementioned recombination issues. Despite the intrinsic interest of these results, the low percentage of positrons in the electron–positron beam (of the order, if not <10%) and the low-density reported (collision-less skin depth much greater than the beam size, forbidding plasma-like behaviour) prevent their application to the laboratory study of e−/e+ plasmas. All these previous experimental attempts have thus not been able to generate e−/e+ beams that present charge neutrality and a plasma-like behaviour, both fundamental pre-requisites for the laboratory study of this state of matter14.
We report here on the first experimental evidence of the generation of a high-density and neutral electron–positron plasma in the laboratory. Its high density  implies that the collision-less skin depth in the plasma is smaller than the plasma transverse size effectively allowing for collective effects to occur. These characteristics, together with the charge neutrality, small divergence
implies that the collision-less skin depth in the plasma is smaller than the plasma transverse size effectively allowing for collective effects to occur. These characteristics, together with the charge neutrality, small divergence  , and high average Lorentz factor (γAV≈15 with a power-law spectral distribution, comparable to what observed in astrophysical jets22) finally open up the possibility of studying the dynamics of e−/e+ plasmas in a controlled laboratory environment.
, and high average Lorentz factor (γAV≈15 with a power-law spectral distribution, comparable to what observed in astrophysical jets22) finally open up the possibility of studying the dynamics of e−/e+ plasmas in a controlled laboratory environment.
Results
Experimental setup
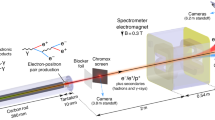
The experiment (shown schematically in Fig. 1a) was carried out using the ASTRA-GEMINI laser system at the Rutherford Appleton Laboratory23, which delivered a laser beam with a central wavelength λL=0.8 μm, energy on target EL≈14 J and a duration of τL=42±4 fs. An f/20 off-axis parabola focussed this laser beam (focal spot with full-width half-maximum (27±3 μm) containing ∼60% of the laser energy, resulting in a peak intensity of ≃3 × 1019 W cm−2) onto the edge of a 20-mm-wide supersonic He gas jet doped with 3.5% of N2. A backing pressure of 45 bar was found to be optimum in terms of maximum electron energy and charge of the accelerated electron beam as resulting from ionization injection24,25 in the gas jet. Optical interferometry of the laser–gas jet interaction indicates this gas–pressure to correspond to a plasma density of npl=(6.0±0.2) × 1018 cm−3. This interaction produced a reproducible electron beam (shot-to-shot fluctuation in charge and maximum energy below 10%) with a broad spectrum with maximum energy of the order of 600 MeV, full-width half-maximum divergence of 2 mrad and an overall charge of (0.3±0.1) nC, corresponding to (1.9±0.6) × 109 electrons (see Fig. 1b for typical electron spectra and their average). This electron beam was then directed onto a Pb solid target of different thicknesses covering multiples of the material’s radiation length (d=0.5, 1, 1.5, 2, 2.5, 3 and 4 cm, given that the radiation length for Pb is Lrad≈0.5 cm (ref. 21)). The electrons and positrons escaping from the rear side of the target were then separated and spectrally resolved by a magnetic spectrometer. The details of this detector can be found in the Methods section.
(a) The laser wakefield-accelerated electrons (green spheres) impact onto a solid target, initiating a quantum electrodynamic cascade involving electrons, positrons (red spheres) and photons (blue sinusoids). The escaping electrons and positrons are separated and spectrally resolved using a magnetic spectrometer (details in the text) and a pair of LANEX screens. Plastic and lead shielding was inserted to reduce the noise on the LANEX screens as induced by both the low-energy electrons and gamma-rays generated, at wide angles, during the laser–gas and electron–solid target interactions. (b) Typical measured spectra of the electron beam without the solid target. Dashed green lines depict single-shot electron spectra, whereas the solid brown line is an average over five consecutive shots. (c) Typical positron signal, as recorded by the LANEX screen, for 0.5 cm of Pb. The image is to scale. The white dashed lines depict the projection of the magnet gap, whereas the grey dashed lines depict the position of 0.2, 0.5 and 1 GeV positrons on the LANEX screen.
Experimental results
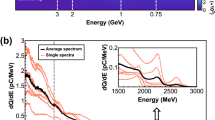
A scan in target thickness was performed in multiples of its radiation length and the obtained positron spectra, each resulting from an average over five consecutive shots, are depicted in Fig. 2 (see Fig. 1c for the raw signal recorded on the LANEX screen for d=0.5 cm). All spectra are in good agreement with the ones resulting from matching simulations using the Monte Carlo scattering code FLUKA, which accounts for electromagnetic cascades during the passage of an electron beam through a solid target26 (see Methods section). A maximum positron energy of EMAX=600 MeV is obtained for d≈Lrad (that is, 5 mm; Fig. 2a), whereas a maximum positron yield is obtained for d≈2Lrad. For thicker targets, the maximum energy gradually decreases as it should be expected due to increased probability of energy loss during the propagation of the generated positrons through the rest of the solid target. For a similar reason, a thicker solid target allows a lower number of electrons and positrons to escape it. This is quantitatively shown in Fig. 3, which depicts the measured number of electrons and positrons (energy exceeding 120 MeV; see Methods section) at the exit of a solid target, as a function of its thickness.
Measured positron spectra, as resulting from the average over five consecutive shots, (solid lines) compared with that obtained from FLUKA simulations (dashed lines) for d=5 mm (a), d=2 cm (b) and d=4 cm (c). In this latter case, also the spectrum of the electrons escaping the target is plotted. Its similarity with the positron spectrum is a clear indication of the generation of a neutral electron–positron pair beam. The inset in a shows the simulated positron spectrum at low energy for d=5 mm, indicating a Jüttner–Synge distribution.
(a) Measured (blue circles) and simulated (red crosses) number of positrons  as a function of the Pb thickness (
as a function of the Pb thickness ( , see main text). The green dashed line represents the analytical prediction (discussed in the text). (b) Measured (blue circles) and simulated (red crosses) number of electrons
, see main text). The green dashed line represents the analytical prediction (discussed in the text). (b) Measured (blue circles) and simulated (red crosses) number of electrons  as a function of the Pb thickness (
as a function of the Pb thickness ( , see main text). The green dashed line represents the analytical prediction (discussed in the text). For these two frames, error bars lie within the size of the circles. (c) Percentage of positrons in the leptonic jet: measured (full blue circles), simulated (red crosses) and analytical prediction (green dashed lines). For all panels, the error bars mainly arise from shot-to-shot fluctuations. FLUKA simulations indicate that the overall number of relativistic electrons and positrons (Ee≥1 MeV) behave in a similar manner. The percentage of positrons in the beam reaches ∼50% for d>2.5 cm≈5Lrad.
, see main text). The green dashed line represents the analytical prediction (discussed in the text). For these two frames, error bars lie within the size of the circles. (c) Percentage of positrons in the leptonic jet: measured (full blue circles), simulated (red crosses) and analytical prediction (green dashed lines). For all panels, the error bars mainly arise from shot-to-shot fluctuations. FLUKA simulations indicate that the overall number of relativistic electrons and positrons (Ee≥1 MeV) behave in a similar manner. The percentage of positrons in the beam reaches ∼50% for d>2.5 cm≈5Lrad.
In order to quantitatively explain the observed trends, we have employed a simple analytical model for a quantum electrodynamic cascade that only includes the emission of photons by electrons and positrons via bremsstrahlung27 and the creation of an electron–positron pair by a photon28, both processes occurring in the field of a heavy atom. We thus neglect additional energy losses as resulting, for instance, from Compton scattering with the electrons of the atoms and from the ionization of the atoms themselves (see Methods section). This model is able to qualitatively reproduce the experimental trends (dashed green curves in Fig. 3), provided that a constant re-scaling factor of about 0.75 is adopted for the absolute yield of both the electrons and positrons. This overestimate is easily understood, as the semi-analytical model does not take into account a number of energy loss mechanisms, such as Compton scattering and the ionization of atoms29. Once this re-scaling factor is applied, the analytical model reproduces the experimental data within a few per cent, clearly indicating that the only processes of bremsstrahlung and electron/positron pair production in the nuclear field are the dominant mechanisms leading to the generation of the detected electron/positron beam.
Let us now turn our attention to the total positron fraction in the leptonic beam  as a function of the target thickness (plotted in Fig. 3c). For d≈Lrad, the positrons account for ∼8–10% of the overall beam owing to the fact that most of the primary electrons are able to escape the target (consistently with the results reported in ref. 21). However, as we increase the target thickness, this ratio increases up to a point where the positrons account for almost 50% of the leptonic jet (d≥2.5 cm; Figs 3c and 4 for the overall charge imbalance in the leptonic beam and its simulated spatial distribution, respectively). In this case, not only the integrated number of electrons and positrons is similar but also their spectrum (Fig. 2c), further indication that almost all the electrons and positrons escaping the target arise from pair production. A positron percentage in the beam of the order of 50% is preserved also if the target thickness is increased; however, we will focus our attention only on d=2.5 cm, since it provides the highest density of the neutral e−/e+ beam. Simulations confirm that the majority of positrons are generated with energies of the order of a few MeV following a Jüttner–Synge distribution, which is commonly assumed for relativistic thermalized plasmas30 (see, as an example, the inset in Fig. 2a). We thus refer to the experimentally measured number of e− and e+
as a function of the target thickness (plotted in Fig. 3c). For d≈Lrad, the positrons account for ∼8–10% of the overall beam owing to the fact that most of the primary electrons are able to escape the target (consistently with the results reported in ref. 21). However, as we increase the target thickness, this ratio increases up to a point where the positrons account for almost 50% of the leptonic jet (d≥2.5 cm; Figs 3c and 4 for the overall charge imbalance in the leptonic beam and its simulated spatial distribution, respectively). In this case, not only the integrated number of electrons and positrons is similar but also their spectrum (Fig. 2c), further indication that almost all the electrons and positrons escaping the target arise from pair production. A positron percentage in the beam of the order of 50% is preserved also if the target thickness is increased; however, we will focus our attention only on d=2.5 cm, since it provides the highest density of the neutral e−/e+ beam. Simulations confirm that the majority of positrons are generated with energies of the order of a few MeV following a Jüttner–Synge distribution, which is commonly assumed for relativistic thermalized plasmas30 (see, as an example, the inset in Fig. 2a). We thus refer to the experimentally measured number of e− and e+  with the subscript NEXP, whereas we will refer to their simulated number
with the subscript NEXP, whereas we will refer to their simulated number  with the subscript NFLUKA. For d=2.5 cm, we thus have
with the subscript NFLUKA. For d=2.5 cm, we thus have  and
and  (Fig. 5a). Taking the appropriate moment of the distribution function, the averaged Lorentz factor of the beam is typically of the order of a few tens (γAV≈15 for d=2.5 cm). FLUKA simulations indicate a divergence of the beam to be energy dependent in a range of 5–20 mrad (ref. 31).
(Fig. 5a). Taking the appropriate moment of the distribution function, the averaged Lorentz factor of the beam is typically of the order of a few tens (γAV≈15 for d=2.5 cm). FLUKA simulations indicate a divergence of the beam to be energy dependent in a range of 5–20 mrad (ref. 31).
Normalized spatial distribution of the electrons (a) and positrons (b) at the rear surface of a 2.5 cm Pb foil, as simulated using FLUKA (details of the simulation in the Methods section). (c) Resulting spatially resolved percentage of positrons in the leptonic beam. The positron percentage oscillates between 45 and 49% across the whole leptonic beam. (d) Simulated spectrum of the electrons (solid green line) and positrons (dashed brown line) at the rear surface of the 2.5 cm Pb foil. Charge imbalance is found only in the low-energy part of the spectrum (energy of the order of 5 MeV).
(a) Number of relativistic electrons ( , green crosses) and positrons (
, green crosses) and positrons ( , brown circles) in the beam as a function of the thickness d of the solid target. (b) Density of relativistic electrons (green crosses) and positrons (brown empty circles) as a function of the thickness d of the solid target. The solid lines represent the density in the laboratory reference frame, whereas dashed lines represent the beam proper density. A neutral electron–positron plasma is obtained for d≥2.5 cm. Lines are drawn only as a guide for the eye.
, brown circles) in the beam as a function of the thickness d of the solid target. (b) Density of relativistic electrons (green crosses) and positrons (brown empty circles) as a function of the thickness d of the solid target. The solid lines represent the density in the laboratory reference frame, whereas dashed lines represent the beam proper density. A neutral electron–positron plasma is obtained for d≥2.5 cm. Lines are drawn only as a guide for the eye.
It must be pointed out that the propagation of an ultra-relativistic electron beam through a high-Z solid target can only asymptotically give a perfectly neutral e−/e+ beam. Additional scattering mechanisms with the atomic electrons, such as Compton, Moller and Bhabha scattering, will in fact slightly increase the electrons number, especially at low energies. FLUKA simulations take all these processes into account and indeed predict an average percentage of positrons, for d=2.5 cm, of 46%. The discrepancy between electron and positron number is exclusively at low energies ( ; Fig. 4d). Most importantly, the electron and positron populations present very similar spatial distributions (Fig. 4a,b) leading to an almost uniform positron percentage in the e−/e+ beam (between 45 and 49%; Fig. 4c). As we shall see later, this slight charge imbalance does not affect the plasma dynamics, which can then be effectively considered to be neutral.
; Fig. 4d). Most importantly, the electron and positron populations present very similar spatial distributions (Fig. 4a,b) leading to an almost uniform positron percentage in the e−/e+ beam (between 45 and 49%; Fig. 4c). As we shall see later, this slight charge imbalance does not affect the plasma dynamics, which can then be effectively considered to be neutral.
A fundamental requisite for the laboratory study of e−/e+ plasmas is that they must present collective behaviour in their dynamics. Collective (that is, plasma-like) effects are likely to occur in the beam only if its transverse size DB is larger than the collision-less skin depth (lskin≃c/ωprop, with ωprop being the relativistic plasma frequency). The beam density is determined by the temporal duration of the beam (that relates to its longitudinal extent) and its transverse size. The primary electron beam exits the gas jet with a typical temporal duration comparable to half the plasma period within the gas32: τpl≃(13.0±0.3) fs. The semi-analytical model for the quantum cascade inside the Pb indicates an average temporal spreading across different spectral components of the beam of the order of 1–3 fs, resulting in a beam duration of  . As intuitively expected, the lower energy electrons and positrons will escape the solid target in a wider area if compared with their higher energy counterparts. FLUKA simulations confirm this expectation and indicate, for d=2.5 cm, a maximum transverse size of the beam of the order of DB≃200±30 μm. For these parameters, we thus obtain a particle density in the laboratory reference frame of the order of ne≃(1.8±0.7) × 1016 cm−3, implying a beam proper density of nprop=ne/γAV≃(1.5±0.5) × 1015 cm−3 (Fig. 5b). The relativistically corrected collision-less skin depth of the beam is thus lskin≃c/ωprop(160±30) μm. This value is smaller than the beam transverse size, indicating that the generated particle beam is a neutral e−/e+ plasma. It is interesting to note that the occurrence of collective behaviour (that is, the situation in which DB/lskin≥1) does not depend on the beam transverse size DB since, based on the considerations presented above, it can be expressed as:
. As intuitively expected, the lower energy electrons and positrons will escape the solid target in a wider area if compared with their higher energy counterparts. FLUKA simulations confirm this expectation and indicate, for d=2.5 cm, a maximum transverse size of the beam of the order of DB≃200±30 μm. For these parameters, we thus obtain a particle density in the laboratory reference frame of the order of ne≃(1.8±0.7) × 1016 cm−3, implying a beam proper density of nprop=ne/γAV≃(1.5±0.5) × 1015 cm−3 (Fig. 5b). The relativistically corrected collision-less skin depth of the beam is thus lskin≃c/ωprop(160±30) μm. This value is smaller than the beam transverse size, indicating that the generated particle beam is a neutral e−/e+ plasma. It is interesting to note that the occurrence of collective behaviour (that is, the situation in which DB/lskin≥1) does not depend on the beam transverse size DB since, based on the considerations presented above, it can be expressed as:  for our experimental parameters (here N indicates the overall number of leptons in the beam).
for our experimental parameters (here N indicates the overall number of leptons in the beam).
Discussion
The presented characteristics of the e−/e+ plasmas generated in our experiment are appealing for the laboratory study of the dynamics of this exotic state of matter. As an example, a particularly active area of research in this direction is the determination of the growth and evolution of kinetic instabilities, which are extensively modelled in order to interpret peculiar astrophysical observations such as the emission of gamma-ray bursts33,34,35,36. It is widely accepted that these ultra-bright bursts result from synchrotron radiation generated via relativistic shocks triggered during the propagation of an electron–positron beam through the low-density intergalactic medium37. This scenario is now reproducible in a laser-driven experiment in which the photoionized residual low-density gas inside the target chamber38 can act as the background electron-ion plasma. In this case, the growth rate for transverse instabilities can be estimated as:  (ref. 13), with βspread and ωei being the velocity spread of the e−/e+ beam and the plasma frequency of the e−-ion plasma, respectively. It is worth noticing that in the ultra-relativistic case, the weak dependence of the growth rate on the beam velocity spread significantly relaxes constraints on the spectral shape of the electron–positron beam. We can assume ωei≈1.5 × 1012 Hz (nei≈6 × 1014 cm−3 as resulting from full photoionization of the background gas) and βspread≈0.1 (β=0.87 and β≈1 for a 1 MeV and a 500 MeV particle, respectively). We thus have ΓTR=5 × 1011 Hz for γAV=15 implying a typical time for the instability to grow of the order of 2 ps. Numerical simulations indicate, in the initial instants of the instability, that up to 10% of the average particle energy in the beam can be transformed into electromagnetic fields in the plasma implying fields with an amplitude of the order of the megagauss; once saturation is reached, this value drops to ∼1% (ref. 13). It is worth noticing that this is similar to what expected for gamma-ray bursts (0.1–1%; ref. 39). This timescale and field amplitude are within reach of plasma radiography techniques such as proton imaging40, a highly encouraging factor for the application of these plasmas for laboratory astrophysics.
(ref. 13), with βspread and ωei being the velocity spread of the e−/e+ beam and the plasma frequency of the e−-ion plasma, respectively. It is worth noticing that in the ultra-relativistic case, the weak dependence of the growth rate on the beam velocity spread significantly relaxes constraints on the spectral shape of the electron–positron beam. We can assume ωei≈1.5 × 1012 Hz (nei≈6 × 1014 cm−3 as resulting from full photoionization of the background gas) and βspread≈0.1 (β=0.87 and β≈1 for a 1 MeV and a 500 MeV particle, respectively). We thus have ΓTR=5 × 1011 Hz for γAV=15 implying a typical time for the instability to grow of the order of 2 ps. Numerical simulations indicate, in the initial instants of the instability, that up to 10% of the average particle energy in the beam can be transformed into electromagnetic fields in the plasma implying fields with an amplitude of the order of the megagauss; once saturation is reached, this value drops to ∼1% (ref. 13). It is worth noticing that this is similar to what expected for gamma-ray bursts (0.1–1%; ref. 39). This timescale and field amplitude are within reach of plasma radiography techniques such as proton imaging40, a highly encouraging factor for the application of these plasmas for laboratory astrophysics.
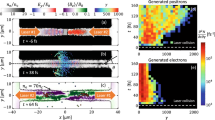
In order to check the validity of our estimates, we have carried out three-dimensional (3D) particle-in-cell (PIC) simulations using the PIC code OSIRIS41,42 (see Methods section). Simulation results are illustrated in Fig. 6. During its propagation through a denser e−-ion plasma, the e−/e+ is subject to the Weibel/current filamentation instability leading to the formation of electron and positron filaments with thicknesses of the order of the beam skin depth. The electron and positron filaments spatially separate from each other leading to net localized currents and the generation of the corresponding azimuthal magnetic field structures with maximum amplitudes of the order of 40 T in the middle of the bunch. At early times, the simulations show that the transverse scale length of the filaments is even shorter than the initial beam skin depth. To further understand the impact of charge neutrality on the instability onset, additional 3D simulations were performed using a purely electronic bunch of same characteristics. In this case, the electron bunch generates plasma wakefields, and neither filamentation of the beam (insets in Fig. 6c) nor the generation of strong magnetic fields (inset Fig. 6d) are observed. These results corroborate the expectation that current filamentation instability growth can be controlled by changing the beam overall total charge and it is maximized for a purely neutral e−/e+ plasma.
Simulation results of the propagation of an e−/e+ plasma through an e−-ion plasma. The first row depicts the results for a perfectly neutral beam (50% electrons and 50% positrons). (a) Electron (blue) and positron (red) density isosurfaces showing growth of the Weibel instability at the back of the bunch. (b) Magnetic field (Bθ) filaments due to the Weibel instability, where the Bθ lies on the plane transverse to bunch propagation direction. (c) Fireball bunch density slice taken at the position of the dashed line in a. (d) Corresponding magnetic Bθ filaments taken at the same location. The insets in c,d show the electron density and magnetic field corresponding to the propagation of a purely electronic beam showing no onset of filamentation. Frames (e,f) depict the results for an analogous simulation, with the only difference that now the positrons account only for 45% of the beam. The frames show slices of the electron (blue) and positron (red) spatial distribution, similar to frame a. (g) Comparison between the magnetic field growth for the case of a purely neutral beam (blue) and a slightly asymmetric beam (45% of positrons, red). For what concerns the plasma dynamics, the two cases are virtually undistinguishable.
Finally, we performed an additional 3D PIC simulation devoted at studying whether a slight charge imbalance in the e−/e+ plasma could result in a change in the plasma dynamics if compared with the idealized perfectly neutral plasma scenario. We have thus maintained exactly the same conditions as the other simulation, with the only difference that now the positron account for 45% of the plasma population, in order to match our experimental findings more closely. The obtained spatial distribution of the e−/e+ plasma after propagation through the background electron/ion plasma is shown in Fig. 6e,f, indicating essentially no difference if compared with the purely neutral case. This statement is corroborated by the growth of magnetic fields due to Weibel instability. This is plotted in Fig. 6g that shows virtually the same magnetic field growth for the purely neutral case (blue line) and for the slight charge imbalance (red). For the point of view of studying electron–positron plasma dynamics in the laboratory, the e−/e+ plasma generated in our experiment is virtually indistinguishable from the idealized purely neutral beam.
On the other hand, the beam might also be susceptible to longitudinal instabilities34,43, which would induce a broadening of the e−/e+ spectrum and generation of strong fields in the background plasma. For d=4 cm (neutral beam), the measured electron and positron spectra are indeed flatter than the ones predicted by FLUKA, which does not include collective behaviour of the beam particles during propagation through the background e−-ion plasma (Fig. 2c). For d=0.5 cm (highly charged beam), simulations and experiments agree much more closely. The spectral flattening may also be produced by kinetic self-focusing of the beam44,45.
In conclusion, we have reported on the first creation of a neutral electron–positron plasma in the laboratory. Its overall charge neutrality and plasma-like behaviour are an absolute novelty in the field of experimental physics and, in conjunction with the small divergence and high energy of these plasmas, finally allow for the laboratory study of this unique state of matter.
Methods
The electron–positron spectrometer
The magnetic spectrometer comprised a pin-hole entrance with a diameter of ∼15 mm through 5 cm of plastic followed by 5 cm of lead. This plastic–lead wall was indeed necessary in order to shield the particle detectors from noise generated during the electron beam impact onto the solid target. After this, a dipole permanent magnet (B=0.8 T, length of 10 cm) was inserted to spectrally resolve the electrons and the positrons, which were recorded by two LANEX screens46. This arrangement allowed us to resolve particle energies from 120 MeV to 1.2 GeV. The LANEX screens were cross-calibrated using absolutely calibrated Imaging Plates47. The small difference in stopping power (of ∼2%; ref. 48) between electrons and positrons was taken into account in calibrating the LANEX screens. Every electron or positron spectrum shown in the manuscript results from an average over five consecutive shots. The energy resolution of the spectrometer can be approximated in the ultra-relativistic limit, as:

Where Ds is the distance from the source to the magnet entrance, Dl is the distance from the entrance of the magnet to the detector (1 m), RL≈E/(ecB) is the radius of curvature of the particle with energy E and charge e in the magnetic field B, θs=15 mrad is the angular acceptance of the detector, and Lm (10 cm) is the length of the magnet. For the energies of interest in our experiment (120≤E[MeV]≤300), the energy resolution is between 10 and 20%.
FLUKA simulations
FLUKA is a nuclear physics Monte Carlo scattering code that accounts for electromagnetic cascades during the passage of an electron beam through a solid target26. The numerical model for the quantum electromagnetic cascade is routinely checked and constantly improved to take into account any refinement in cross-section measurements in conventional accelerators. As an input for the simulation, we assume an electron beam with the spectral shape depicted in Fig. 1b (brown solid line), 2 mrad full-width half-maximum divergence and 10 μm radius source size. The electron beam then interacts with a lead target of different thicknesses and 1 cm transverse size, placed 1 cm downstream of the electron beam source. Iterations (106) were used in order to achieve a good statistical representation in the Monte Carlo method. Every numerical result reported originates from an average over five identical runs in order to minimize any stochastic error arising from the random seed generator of the code. The results of the simulations, obtained in units of particles per initial electron, were then rescaled with the measured number of primary electrons, giving a good quantitative agreement with the experimental data.
Semi-analytical model for the quantum cascade
We assume a quantum electrodynamics cascade shower involving only electrons, positrons and photons at energies much larger than the electron rest energy m (units with h=c=1 are assumed hereafter). We thus neglect additional electron and positron energy losses as resulting, for instance, from Compton scattering with the electrons of the atoms and from the ionization of the atoms themselves. The only processes to be included in the kinetic equations are thus the emission of photons by electrons and positrons via bremsstrahlung and the creation of an electron–positron pair by a photon, both processes occurring in the field of a heavy atom. By setting the target thickness d in units of the radiation length Lrad, that is, ℓ=d/Lrad, the electron/positron distribution functions f±(E,ℓ) and the photon distribution function fγ(E,ℓ) satisfy the kinetic equations29:


where the functions


with μ0=7/9−b/3 and b=1/18 log(183/Z1/3), are related to the cross-section of bremsstrahlung and pair photo-production in the field of a heavy atom with atomic number Z (see ref. 29 for details). By numerically solving these equations, we are able to reproduce the experimental trends well (dashed green curves in Fig. 3 of the manuscript), provided that a constant re-scaling factor of 0.75 is adopted for the absolute yield of both the electrons and positrons. The overestimation of the experimental results by this simplified model is easily understood, as the latter does not take into account a number of braking mechanisms, such as Compton scattering for photons and the ionization of atoms for electrons and positrons29. On the one hand, braking mechanisms such as ionization affect essentially relativistic electrons and positrons in the same way49. On the other hand, however, our analytical model cannot predict charge asymmetries brought in by injection of atomic electrons in the cascade following these scattering processes. This is the reason why, for a target thickness of 2.5 cm, our semi-analytical model predicts a 50% percentage of positrons in the leptonic beam, whereas our FLUKA simulations indicate a positron percentage of the order of 46%.
Starting from a simple model, where each electron/positron (photon) after a radiation length emits a photon (transforms into an electron–positron pair) with half of the energy of the initial electron (with the electron and positron sharing half of the energy of the initial photon), it can also be shown that the maximum yield of positrons with an energy exceeding E can be estimated to occur for a target thickness dopt∼Lrad log(〈Ee〉/E)/log(2) (ref. 29), where 〈Ee〉 is the average energy of the initial electron distribution (Fig. 1b). In our case, it results 〈Ee〉≈456 MeV and dopt∼1.1 cm (≃1.96 Lrad) in good agreement with the experimental results.
The PIC simulations
The simulations were performed with the fully relativistic, massively parallel, PIC code OSIRIS41,42. OSIRIS has been extensively used to explore relativistic beam plasma interaction scenarios, and has been widely applied to model the Weibel instability in various configurations (see, for instance, refs 13, 14, 41, 42, 50). In OSIRIS, the electric and magnetic fields are defined in a grid. The trajectory of each simulation particle is determined through the relativistic equations of motion by interpolating the grid fields to the position of the particle. Current density is deposited onto the grid, and used to advance the electric and magnetic fields through Maxwell’s equations discretized using a finite-difference scheme. In this section, we give the numerical parameters for the simulations. Simulations used a moving window with dimensions 1.5 × 100 × 100 (c/ωp)3 divided into 75 × 1,000 × 1,000 cells with 2 × 1 × 1 particles per cell for plasma electrons and for beam particles. Here ωp is the plasma frequency of the background electron–proton plasma, which has a density of nei=1016 cm−3. A charge–neutral beam constituted by electrons and positrons was initialized at the entrance of the plasma. The density profile for electrons and positrons is given by  where nb0=10 nei=1017 cm−3, σξ=0.22 c/ωp=11.7 μm and σr=10 c/ωp=530 μm are the bunch peak density, length and transverse waist, respectively. The particles’ Lorentz factor is initialized to be
where nb0=10 nei=1017 cm−3, σξ=0.22 c/ωp=11.7 μm and σr=10 c/ωp=530 μm are the bunch peak density, length and transverse waist, respectively. The particles’ Lorentz factor is initialized to be  .
.
Additional information
How to cite this article: Sarri, G. et al. Generation of neutral and high-density electron–positron pair plasmas in the laboratory. Nat. Commun. 6:6747 doi: 10.1038/ncomms7747 (2015).
Change history
15 May 2015
This Article was originally published under NPG's License to Publish, which has now been changed to CC BY 4.0. The PDF and HTML versions of the paper have been modified accordingly.
References
Blandford, R. D. & Znajek, R. L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 179, 433–456 (1977).
Begelman, M. C., Blandford, D. & Rees, J. Theory of extragalactic radio sources. Rev. Mod. Phys. 56, 255–351 (1984).
Goldreich, P. & Julian, W. H. Pulsar electrodynamics. Astrophys. J. 157, 869–880 (1969).
Wardle, J. F. C. et al. Electron-positron jets associated with the quasar 3C279. Nature 395, 457–461 (1998).
Abdo, A. A. et al. Fermi observations of high-energy gamma-ray emission from GRB 080916C. Science 323, 1688–1693 (2009).
Lyne, A. G. et al. A double-pulsar system: a rare laboratory for relativistic gravity and plasma physics. Science 303, 1153–1157 (2004).
Tavani, M. et al. Discovery of powerful gamma-ray flares from the crab nebula. Science 331, 736–739 (2011).
Gruzinov, A. Gamma-ray burst phenomenology, shock dynamo, and the first magnetic fields. Astrophys. J. 563, L15–L18 (2001).
Chang, P., Spitkovsky, A. & Arons, J. A Long-term evolution of magnetic turbulence in relativistic collisionless shocks: electron-positron plasmas. Astrophys. J. 674, 378–387 (2008).
Keshet, U., Katz, B., Spitkovsky, A. & Waxman, E. Magnetic field evolution in relativistic unmagnetized collisionless shocks. Astrophys. J. 693, L127–L130 (2009).
Greaves, R. G., Tinkle, M. D. & Surko, C. M. Creation and uses of positron plasmas. Phys. Plasmas 1, 1439–1446 (1994).
Pedersen, T. S. et al. Plans for the creation and studies of electron-positron plasmas in a stellarator. New J. Phys. 41, 035010 (2012).
Fonseca, R. A. et al. Three-dimensional Weibel instability in astrophysical scenarios. Phys. Plasmas 10, 1979–1984 (2003).
Muggli, P. et al. Interaction of ultra-relativistic fireball beam with plasma. Preprint at http://ArXiv:1306.4380v1 (2013).
Surko, C. M. & Greaves, R. G. A multicell trap to confine a large number of positrons. Rad. Phys. Chem. 68, 419–425 (2003).
Chen, H. et al. Relativistic positron creation using ultraintense short pulse lasers. Phys. Rev. Lett. 102, 105001 (2009).
Chen, H. et al. Relativistic quasimonoenergetic positron jets from intense laser-solid interactions. Phys. Rev. Lett. 105, 015003 (2010).
Gahn, C. et al. Generating positrons with femtosecond-laser pulses. Appl. Phys. Lett. 77, 2662–2664 (2000).
Gahn, C. et al. Generation of MeV electrons and positrons with femtosecond pulses from a table-top laser system. Phys. Plasmas 9, 987–999 (2002).
Di Piazza, A., Müller, C., Hatsagortsyan, K. Z. & Keitel, C. H. Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 84, 1177–1228 (2012).
Sarri, G. et al. Table-top laser-based source of femtosecond, collimated, ultrarelativistic positron beams. Phys. Rev. Lett. 110, 255002 (2013).
Hoshino, M. et al. Relativistic magnetosonic shock waves in synchrotron sources: shock structure and nonthermal acceleration of positrons. Astrophys. J. 390, 454–479 (1992).
Hooker, C. J. et al. The Astra Gemini project - a dual-beam petawatt Ti:Sapphire laser system. J. Phys. IV 133, 673–677 (2006).
Esarey, E., Schroeder, C. B. & Leemans, W. P. Physics of laser-driven plasma-based electron accelerators. Rev. Mod. Phys. 81, 1229–1285 (2009).
Clayton, C. E. et al. Self-guided laser wakefield acceleration beyond 1 GeV using ionization-induced injection. Phys. Rev. Lett. 105, 105003 (2010).
Battistoni, G. et al. The FLUKA code: description and benchmarking. AIP Conf. Proc. 896, 31–49 (2007).
Koch, H. W. & Motz, J. Bremsstrahlung cross-section formulas and related data. Rev. Mod. Phys. 31, 920–955 (1959).
Beresteskii, V. B., Lifshitz, E. M. & Pitaevskii, L. P. Quantum Electrodynamics Butterworth-Heinemann (2008).
Rossi, B. High-Energy Particles Prentice-Hall (1952).
Synge, J. L. The Relativistic Gas North-Holland Pub. Co. (1957).
Sarri, G. et al. Laser-driven generation of collimated ultra-relativistic positron beams. Plasma Phys. Control. Fusion 55, 124017 (2013).
Mangles, S. P. D. et al. Laser-wakefield acceleration of monoenergetic electron beams in the first plasma-wave period. Phys. Rev. Lett. 96, 215001 (2006).
Amano, T. & Kirk, J. G. The role of superluminal electromagnetic waves in pulsar winds termination shocks. Astrophys. J. 770, 18 (2013).
Sironi, L. & Giannios, D. Relativistic pair beams from TeV blazars: a source of reprocessed GeV emission rather than IGM heating. Preprint at http://ArXiv:1312.4538 (2013).
Schlickeiser, R., Ibscher, D. & Supsar, M. Plasma effects on fast pair beams in cosmic voids. Astrophys. J. 758, 102 (2012).
Schlickeiser, R., Krakau, S. & Supsar, M. Plasma effects on fast pair beams: reactive versus kinetic instability of parallel electrostatic waves. Astrophys. J. 777, 49 (2013).
Ferriere, K. M. The interstellar environment of our galaxy. Rev. Mod. Phys. 73, 1031–1066 (2001).
Ahmed, H. et al. Time-resolved characterization of the formation of a collisionless shock. Phys. Rev. Lett. 110, 205001 (2013).
Panaitescu, A. & Kumar, P. Properties of relativistic jets in gamma-ray burst afterglows. Astrophys. J. 571, 779–789 (2002).
Sarri, G. et al. The application of laser-driven proton beams to the radiography of intense laser-hohlraum interactions. New J. Phys. 12, 045006 (2010).
Fonseca, R. A. et al. OSIRIS: a three-dimensional, fully relativistic particle in cell code for modeling plasma based accelerators. Lect. Notes Comp. Sci. 2331, 342–351 (2002).
Fonseca, R. A. et al. One-to-one direct modeling of experiments and astrophysical scenarios: pushing the envelope on kinetic plasma simulations. Plasma Phys. Control. Fusion 50, 124034 (2008).
Sudan, R. N. Handbook of Plasma Physics Vol. 1, North-Holland Publishing (1984).
Craxton, R. S. & McCrory, R. L. Hydrodynamics of thermal self-focusing in laser plasmas. J. Appl. Phys. 56, 108–117 (1984).
Reville, B. & Bell, A. R. A filamentation instability for streaming cosmic rays. Mon. Not. R. Astron. Soc. 419, 2433–2440 (2011).
Glinec, Y. et al. Absolute calibration for a broad range single shot electron spectrometer. Rev. Sci. Instrum. 77, 103301 (2006).
Tanaka, K. A. et al. Calibration of imaging plate for high energy electron spectrometer. Rev. Sci. Instrum. 76, 013507 (2005).
Rohrlich, F. & Carlson, B. C. Positron-electron differences in energy loss and multiple scattering. Phys. Rev 93, 38–44 (1954).
Olive, K. A. et al. (Particle Data Group). Review of particle physics. Chin. Phys. C 38, 090001 (2014).
Silva, L. O. et al. Interpenetrating plasma shells: near-equipartition magnetic field generation and nonthermal particle acceleration. Astrophys. J. Lett. 596, L121–L124 (2003).
Acknowledgements
We are grateful for the support of the Central Laser Facility staff. The work of W.S., A.G.R.T., K.K. and M.V. was partially supported by the funding schemes National Science Foundation CAREER (grant 1054164) and National Science Foundation/Domestic Nuclear Detection Office (award no. F021166). G.S. and M.Z. wish to acknowledge financial support from the Engineering and Physical Sciences Research Council (grants: EP/L013975/1 and EP/I029206/1, respectively). LAG and G.G. acknowledge financial support from Consiglio Nazionale delle Ricerche (ELI-Italy) and Istituto Nazionale di Fisica Nucleare (CN5-g-RESIST). J.V., N.S. and L.O.S. wish to acknowledge the European Research Council (ERC-2010-AdG grant no. 267841), Fundação para a Ciência e Tecnologia, through grant EXPL/FIS-PLA/0834/2012. Z.N., S.P.D., J.M.C, K.P. wish to acknowledge financial support from STFC (grant no. ST/J002062/1). Access to the SuperMUC based in Germany at Leibniz research center was obtained through PRACE.
Author information
Authors and Affiliations
Contributions
G.S. and M.Z. conceived the experiment, which was performed by G.S., K.P., J.M.C., W.S., D.D. and M.V., with input from L.A.G., D.S., G.G. and S.K. G.S. and T.D. carried out the data analysis and interpretation with theoretical support provided by A.D.P., C.H.K. and B.R. Particle-in-cell simulations and their analysis were performed by J.V., N.S. and L.O.S. The manuscript was written by G.S., with input from B.R., M.Z., A.D.P., C.H.K., Z.N., A.G.R.T., L.A.G., S.P.D.M. and K.K.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Sarri, G., Poder, K., Cole, J. et al. Generation of neutral and high-density electron–positron pair plasmas in the laboratory. Nat Commun 6, 6747 (2015). https://doi.org/10.1038/ncomms7747
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms7747
This article is cited by
-
Narrow bandwidth, low-emittance positron beams from a laser-wakefield accelerator
Scientific Reports (2024)
-
Charge-neutral, GeV-scale electron-positron pair beams produced using bremsstrahlung gamma rays
Communications Physics (2024)
-
Relaxation of a Two Electron-Temperature Relativistic Hot Electron-Positron-Ion Plasma
Brazilian Journal of Physics (2024)
-
Laboratory realization of relativistic pair-plasma beams
Nature Communications (2024)
-
Laser pulse compression by a density gradient plasma for exawatt to zettawatt lasers
Nature Photonics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.