Introduction

Many systems in Nature present either spatial curvature (e.g. curved space due to presence of stars1 or flow on soap films2) or geometric confinement constraining the degrees of freedom of particles moving on such media, e.g. solar photosphere3, flow between two rotating cylinders and spheres4,5,6, hemodynamics through deformable vessels7, fusion plasmas8 and flow through porous media9, to name but a few. In general, these systems force a fluid to move along non-straight trajectories (curved geodesics), leading to the upsurge of non-inertial forces. We will denote such systems as Campylotic, from the greek word for curved, media. Due to the arbitrary trajectories that particles through a campylotic medium can take, depending on the complexity of the curved space, the flow through these media can present very unusual new transport properties. Campylotic media play a prominent role in all applications where metric curvature has a major impact on the flow structure and topology; biology, astrophysics and cosmology offering perhaps the most natural examples. Indeed, the flow through some specific campylotic media has already been studied, e.g. Taylor-Couette flow and flow through porous media. The Taylor-Couette flow was originally formulated for the case of two concentric, rotating cylinders4,5 and later extended to the case of spheres6,10. On the other hand, continuum descriptions of flow through homogeneous porous media have been already treated as changes in the fluid trajectories, by resorting to the concept of tortuosity, which is the ratio between the straight line distance to the curved path length (due to the presence of obstacles) between two points in the medium. The tortuosity is directly related to the permeability and porosity of the medium9. However, the flow through other complicated structures, like randomly located stars (which is an intrinsically curved space) or many biological systems, to the best of our knowledge, has never systematically been addressed before on quantitative grounds.

Since, in general, this class of flows lacks analytical solutions, their study is inherently dependent on the availability of appropriate numerical methods. Flows in complex geometries, such as cars or airplanes, make a time-honored mainstream of computational fluid dynamics (CFD), a discipline which has made tremendous progress for the last decades11,12. However, campylotic media set a major challenge even to the most sophisticated CFD methods, because the geometrical complexity is often such to command very high spatial accuracy to resolve the most acute metric and topological features of the flow. Therefore, in this work, we also present a new lattice kinetic scheme that can handle flows in virtually arbitrary complex manifolds in a very natural and elegant way, by resorting to a covariant formulation of the lattice Boltzmann (LB) kinetic equation in general coordinates and for curved spaces.

As an additional feature, complex boundary conditions related with a specific geometry, e.g. surface of a sphere, or more sophisticated ones, like Möbius bands and the Klein bottle, can be treated exactly by cubic cells in the contravariant coordinate frame, thereby avoiding the staircase approximations which would result from the use of cubic cells associated with euclidean geometry. For instance, in spherical coordinates, we can construct a lattice with cubic cells of volume δr × δθ × δϕ, being (r, θ, ϕ) the coordinates of each grid point. This feature can also be used to model the microscopic geometry of a porous medium by computing, analytically or numerically, the coordinate system that parametrizes the pore structure and thus, to avoid the staircase approximation of the obstacles. The method is validated quantitatively for very simple campylotic media with geometrical confinements by calculating the critical Reynolds number for the onset of the Taylor-Couette instability in concentric cylinders and spheres5,6,10,13 and applied to the case of two concentric tori.

In this work, by using the new numerical scheme, we simulate the flow through campylotic media consisting of randomly distributed spatial curvature perturbations (see Fig. 1), in the laminar regime. The flow is characterized by the number of curvature perturbations and the average Ricci scalar of the space. The campylotic media explored in this work are static, in the sense that the metric tensor and curvature are prescribed at the outset once and for all and do not evolve self-consistently with the flow. The latter case, which is a major mainstream of current numerical relativity14,15,16,17, especially in the turbulent regime, makes a very interesting subject for future extensions of this work.

Figure 1
figure 1

Streamlines of a three-dimensional fluid moving through a campylotic medium.

The colors denote the scalar of curvature R′ (blue and red for low and high values, respectively). The gray bubbles isosurfaces stand at 1/5 of the maximum curvature of the system.

Full size image

Results

Kinetic theory in general manifolds

In order to study the campylotic media, we develop a lattice Boltzmann approach for curved spaces in general coordinates, taking into account the metric tensor gij and the Christoffel symbols . The former characterizes the way to measure distances in space, while the latter is responsible for the non-inertial forces. The corresponding hydrodynamic equations can be obtained by replacing the partial derivatives by covariant ones, in both, the mass continuity and the momentum conservation equations. After some algebraic manipulations, the hydrodynamic equations read as follows: ∂tρ + (ρui);i = 0 and , where the notation; i denotes the covariant derivative with respect to spatial component i (see SI). The energy tensor Tij is given by, , where P is the hydrostatic pressure, ui the i-th contravariant component of the velocity, gij the inverse of the metric tensor, ρ is the density of the fluid and μ is the dynamic shear viscosity.

Since lattice Boltzmann methods are based on kinetic theory, we construct our model by writing the Maxwell-Boltzmann distribution and the Boltzmann equation for general manifolds. The former takes the form18:

where g is the determinant of the metric gij and θ is the normalized temperature. The macroscopic and microscopic velocities, ui and ξi are both normalized with the speed of sound , kB being the Boltzmann constant, T0 the typical temperature and m the mass of the particles. Note that the metric tensor appears explicitly in the distribution function, due to the fact that the kinetic energy is a quadratic function of the velocity, uiui = gijuiuj. To recover the macroscopic fluid dynamic equations, we have to extract the moments from the equilibrium distribution function. The four first moments of the Maxwellian distribution function on a manifold are given by,

These moments are sufficient to reproduce the mass and the momentum conservation equations. Here, for simplicity we have used dξ to denote dξ1dξ2dξ3 and the Jacobian of the integration is already included in the Maxwell Boltzmann distribution, through the determinant term .

In the absence of external forces, in the standard theory of the Boltzmann equation, the single particle distribution function f(xi, ξi, t) evolves, according to the equation, , where is the collision term, which, using the BGK approximation, can be written as, , with the single relaxation time τ. This equation can be obtained from a more general expression, , where the total time derivative now includes a streaming term in velocity space due to external forces, , with pi the i-th contravariant component of the momentum of the particles. Using the definition of velocity, ξi = dxi/dt and due to the fact that the particles in our fluid move along geodesics, which implies the equation of motion , we can write the Boltzmann equation, using a procedure based on Ref. 19, as

where we have used the definition of the momentum, pi = mξi. Note that the third term of the left hand side carries all the information on non-inertial forces. The Christoffel symbols and metric tensor are arbitrary and therefore we can model the fluid flow in curved spaces in general coordinates, whose metric tensor is very complicated and/or only known numerically.

Since the contravariant components of the velocity are free of space-dependent metric factors, they lend themselves to standard lattice Boltzmann discretization of velocity space. All the metric and non-inertial information is conveyed into the generalized local equilibria and forcing term, respectively. These features are key to the LB formulation in general manifolds. As an additional feature, even in flat spaces, complex boundary conditions related to a specific geometry, e.g. surface of sphere, in many cases, can be treated exactly by cubic cells in the contravariant coordinate frame, thereby avoiding stair-case approximations typical of cartesian grids.

Studying the campylotic media

To study a genuinely campylotic medium, consisting of randomly located perturbations of spatial intrinsic curvature, we define a coordinate system (x, y, z), such that its metric tensor deviates from the one of a flat space (δij) in the form: , where n labels each local curvature perturbation located at , N is the total number of perturbations, and r0 characterizes the size of the deformation. The choice of this metric tensor is to induce an intrinsic curvature in the space at each point . Note that the coefficient a0 can be either signed, depending on whether a positive or negative curvature is imposed, respectively. In our study, we have chosen to work with positive values of a0, but its sign can be different according to the respective application. In order to understand the effects of the curvature, we will work in the laminar regime to avoid pressure losses due to turbulence. The effects of pressure drops in campylotic media due to fluid turbulence shall be addressed in future work.

The Christoffel symbols are calculated numerically. The flux is calculated by the geometrical relation, , where S is the cross section at the location where the measurements are taken. Since the fluid dynamic equations only contain the metric tensor and its first derivatives (via the Christoffel symbol), it is natural to expect that the flow could be characterized by a quantity that contains the metric tensor and its first derivatives. Although the Christoffel symbols meet this requirement, they are not components of a tensor and therefore they are not invariant under a coordinate system transformation (physics should not depend on the choice of the coordinate system). An invariant, or tensor, that can be used to characterize the system is the Ricci tensor Rik. In this work, we use the Ricci scalar (curvature scalar) which can be calculated from the Ricci tensor, Rij, by contraction of the indices, R′ = gijRij. The relation between the metric tensor and Christoffel symbols and the Ricci tensor can be found in the SI. For sake of generality and to study our system using dimensionless units, we define a characteristic length λ = (V/N)1/3, where V = LxLyLz is the total volume of our system and the local Reynolds number Re = Φr0/(μS). Therefore, the dimensionless size of deformation is defined by . We use a lattice size Lx × Ly × Lz of 128 × 64 × 64 and τ = 1. All quantities will be expressed in numerical units. To drive the fluid through the medium, we add an external force along the x-component, which in all simulations takes the value, fext = 5 × 10−5. The flux in flat space, i.e. in the absence of curvature perturbations is denoted by Φ0.

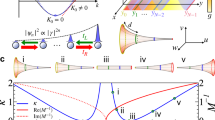
Shown in Fig. 1, are the velocity streamlines, the Ricci scalar R′ and the high-curvature locations, represented by gray isosurfaces. Note that the streamlines are very complex, as the flow can orbit around the spheres before continuing its trajectory21,20. This effect is due to the complex curvature of the space and has no relation to turbulent vortices, given the low Reynolds number (Re ~ 1). Also we can see how the curvature perturbations interact, creating non-spherical shaped isosurfaces.

Fig. 2 shows the flux deficit Φ0 – Φ, as function of the number of curvature perturbations, N. We observe that the flux Φ decreases with N. This effect is due to the interplay between the longer trajectories that particles must take and the acceleration due to the non-inertial forces. Note that, in general, for systems with different configurations (e.g. negative a0), we could expect that the combination of the two effects might lead to higher flux by increasing N. We also see that the flux depends linearly on N for low concentration of curvature perturbations and only sublinearly at higher concentrations. This is due to the fact that at low concentration, the average distance between curvature perturbations is large and consequently each perturbation adds up as a single modification to the total spatial curvature. However, as the concentration is increased, the curvature perturbations start to interfere with each other and consequently the space becomes less curved (decrease of the overall Ricci curvature). The flux is found to obey the following law,

where A1 = 163 ± 2 and N0 = (1.54 ± 0.03) × 104 are fitting parameters. The parameter N0 denotes a characteristic number of curvature perturbations, above which the sublinear behavior sets in (). In dimensionless quantities, this is,

where is the characteristic value above which the sublinear behavior starts to be dominant and provides an “effective radius”, , for each curvature perturbation.

Figure 2
figure 2

Flux through a campylotic medium consisting of randomly located curvature perturbations.

Flux deficit Φ0 − Φ with respect to the flat case, as a function of the number of curvature perturbations for a0 = 0.01, r0 = 2.0 and the Re varying between 0.1 and 0.4. The solid line is the analytical curve according to Eq. (6). Shown in the inset is the normalized average curvature scalar of the space, R/Rmax and the normalized reduced flux 1 − Φ0/Φ as a function of (Re ~ 1 … 1000). Both Ricci scalar and flux deficit exhibit a maximum at intermediate values of . Since the two maxima are slightly shifted with respect to each other, the reduced flow as a function of R exhibits two distinct functional expressions (see next Fig. 3).

Full size image

In the inset of Fig. 2, we observe that by fixing the number of curvature perturbations N = 1024 and the strength a0 = 2 × 10−5 and changing the range of the perturbation, with λ = 8, the difference Φ0 – Φ presents a maximum for a given . Note that this value is similar to . Due to the fact that by increasing r0 the flux Φ decreases, one could think that the Reynolds number would achieve a plateau. However, by analysing our numerical data we have not found such behavior. Furthermore, another interesting result is that the average dimensionless curvature, here defined as R = −106λ2 < R′ > (where < … > means average over space), shows the same qualitative behavior. Since by increasing the metric tensor components decrease monotonically, this maximum is due to the Christoffel symbols (or non-inertial forces), which can be characterized via R. However, the maxima are slightly shifted, due to the fact that the Ricci scalar does not uniquely determine the metric tensor and Christoffel symbols, the quantities that play a key role in the fluid dynamic equations. Taking into account this effect, we can plot the flux deficit Φ0 – Φ as a function of R and find that, indeed, for , the flux decreases by increasing the average curvature R with a different law than for the case of large values of (see inset of Fig. 3). This gives rise to a loop-shaped curve, the reason for this behavior being that the metric tensor is different for and , even if R takes the same value. However, in both cases, the system shows that higher values of the average curvature R always result in a lower flux. The behavior of the flux for is well represented by the following law:

and for the case of ,

where R0 = 5.2 ± 0.1, A2 = 50 ± 2, A3 = 154 ± 4 and Φ′ = 5 ± 1. The quantity R0 is related to the maximum curvature achieved by the system and the intersection of the two laws (see Fig. 3). The other interesting quantity is Φ′, which represents the difference of flux between and , when the curvature scalar becomes zero and it is due to the fact that in both cases, although the space has no curvature, it has nonetheless different metric tensors.

Figure 3
figure 3

Flux deficit, Φ0 − Φ, as a function of the average curvature, R, for large and small values of ϵ.

We have fixed a0 = 0.00002, N = 1024 (Re ~ 1 … 1000). The solid lines denote the analytical curves according to Eqs. (8) and (9). The inset shows the loop which arises by parametrizing the flux-curvature relation in terms of . Here, is the radius at which the Ricci curvature attains its maximum upon increasing . The lower and upper branches correspond to and , respectively.

Full size image

Finally, in order to give a more general description to our campylotic medium, we perform a detailed study of the the flux Φ, as a function of two dimensionless number, Re and . Since Re is not the only dimensionless number that characterizes the flow, we can expect different behaviors depending on how the Re is varied. Therefore, we will change Re by modifying both, the perturbation range r0 and the viscosity μ, separately. In Fig. 4, we can appreciate the dependence of the flux deficit, Φ0 − Φ, as a function of for a fix Reynolds number, Re = 3. Note that fixing the Reynolds number and changing the ratio , implies to vary the number of impurities perturbations. As a consequence, in order to achieve a broad range of values, we decrease the amplitude a0, taking the value of 2 × 10−6. In the domain , we found that the flux decreases following a power law with exponent 3.

Figure 4
figure 4

Flux as a function of the dimensionless numbers Re and ϵ.

Flux deficit, Φ0 − Φ, as a function of the dimensionless number for Re = 3, which decreases following a power law with exponent 3, in the studied regime. In the inset, we can observe the dependence on Re by fixing and varying r0, for different viscosities, ν = 0.55 (green squares), 0.18 (blue circles) and 0.07 (red diamonds).

Full size image

In the inset of Fig. 4, we report the behavior of the flux deficit as a function of the Reynolds number by changing r0, for and different values of the fluid viscosity μ. Here, in order to vary Re, via r0, for fixed and μ, we need to modify both, N and r0. In the regime of Reynolds numbers studied in this work and for a fixed viscosity, the flux increases with the Reynolds number almost linearly upto some critical number, Rec, above which a sublinear behavior is found nearing a plateau. The flux deficit obeys the law,

with B2 = 0.259 ± 0.006 and Rec = 5.8 ± 0.1 for μ = 0.18, B2 = 0.289 ± 0.008 and Rec = 0.75 ± 0.02 for μ = 0.55 and B2 = 0.16 ± 0.005 and Rec = 35.8 ± 0.9 for μ = 0.07. Note that Eq. (10) is satisfied regardless the viscosity of the fluid and we can conclude that by decreasing the viscosity, we increase the critical Reynolds number at which the sublinear regime begins. On the other hand, the insensitivity of the flux deficit at large Reynolds numbers (by changing the interaction range, r0 and therefore, large values of r0) is due to the fact that the average curvature of the system decreases, leading to a flat space and Φ → (1 + B2)Φ0.

Discussion

Summarizing, we have explored the laws that rule the flow through campylotic media consisting of randomly distributed curvature perturbations and shown that, for the configurations studied in this work, curved spaces invariably support less flux than flat spaces. Furthermore, the flux can be characterized by the Ricci scalar, a geometrical invariant that contains the metric tensor and Christoffel symbols. The trajectories of the flow can become very complicated, due to the total curvature of the medium, presenting, in some cases, orbits winding several times around regions with high curvature. To add generality to our study, we have also analyzed the flux transport across the campylotic medium as a function of dimensionless numbers, and Re. Furthermore, we have found that the different laws that characterize the campylotic medium are valid regardless of the viscosity of the fluid, as far as the laminar regime holds. Indeed, further extensions to consider turbulent flows will be a subject of future research.

To calculate the flux in campylotic media, we have developed a new lattice Boltzmann model to simulate fluid dynamics in curved manifolds using an arbitrary coordinate system. The model has been successfully validated (see SI) on the Taylor-Couette instability for the case of two concentric cylinders and spheres, the inner rotating with a given speed and the outer being fixed. We also studied the Taylor-Couette instability in two concentric rotating tori, finding that the critical Reynolds number for the onset of the instability is about ten percent larger than the one for the cylinder. By solving the Navier-Stokes equations for curved spaces in contravariant coordinates, which can be represented on a cubic lattice precisely in the format requested by the lattice Boltzmann formulation, the present model opens up the possibility to study fluid dynamics in complex manifolds by retaining the outstanding simplicity and computational efficiency of the standard lattice Boltzmann method in cartesian coordinates.

Methods

In order to formulate a corresponding lattice Boltzmann model, we implement an expansion of the Maxwell-Boltzmann distribution, Eq. (1), in Hermite polynomials, so as to recover the moments of the distribution function up to third order in velocities, as it is needed to correctly reproduce the dissipation term in the hydrodynamic equations. The expansion of the Maxwell-Boltzmann distribution was introduced by Grad in his 13 moment system22. Since this expansion is performed in velocity space and the metric only depends on the spatial coordinates, we expect such an expansion to preserve its validity also in the case of a general manifold. We have followed a similar procedure as the one described in Refs. 23, 24.

For the discretization of the Maxwell Boltzmann distribution (1) and the Boltzmann equation (5), we need a discrete velocity configuration supporting the expansion up to third order in Hermite polynomials. Our scheme is based on the D3Q41 (three dimensions and 41 velocity vectors) lattice proposed in Ref. 25, which corresponds to the minimum configuration supporting third-order isotropy in three spatial dimensions, along with a H-theorem for future entropic extensions26 of the present work.

In the following, we shall use the notation to denote the i-th contravariant component of the vector numbered λ. Thus, the discrete Boltzmann equation for our model takes the form, , where is the forcing term, which contains the Christoffel symbols and is the discrete form of the Maxwell-Boltzmann distribution, Eq. (1). The relevant physical information about the fluid and the geometry of the system is contained in these two terms. The macroscopic variables are obtained according to the relations, , .

The cell configuration D3Q41 has the discrete velocity vectors: (0, 0, 0), (±1, 0, 0), (±1, ±1, 0), (±1, ±1, ±1), (±3, 0, 0), (0, ±3, 0), (0, 0, ±3) and (±3, ±3, ±3). The speed of sound for this configuration is . With this setup and taking into account that the vectors ξi and ui are normalized by the speed of sound, we obtain the following discrete equilibrium distribution,

where the weights wλ are defined as, , , , , and . The forcing term takes the form

with and δkl the Kronecker delta. In the presence of an external force Fext, this simply extends to .

In order to recover the correct macroscopic fluid equations, via a Chapman-Enskog expansion, the other moments, Eqs. (2), (3) and (4), also need to be reproduced. A straightforward calculation shows that the equilibrium distribution function meets the requirement. The shear viscosity of the fluid can also be calculated as . In this way one can calculate the fluid motion in spaces with arbitrary local curvatures.

We have measured the efficiency vs. standard LB and the resulting overhead (about 3) is almost entirely to be ascribed to the fact that, by relativistic necessity (third order moments to be matched), we work with 41 velocities. Although a detailed head-on comparison remains to be done in future work, such overhead appears perfectly acceptable, especially in view of future applications to relativistic dissipative hydrodynamics in highly complex manifolds. More details about the discretization of this model on a lattice and the numerical validation can be found in the SI.

All simulations in this paper are performed using the smallest system size that keeps the physical results unchanged at increasing the grid resolution. The reason for this choice is that we need to calculate the metric tensor and the Christoffel symbols locally, which calls for a computational compromise. On the one hand, storing the metric tensor and Christoffel symbols as arrays, minimizes the CPU time, at the price of increasing memory requirements. On the other hand, by computing these quantities “on the fly”, memory request is significantly reduced, to the detriment of computational time. For the simulations presented in this work, we have used the former approach (metric and Christoffel symbols as stored as arrays), so that we cannot compute very large system sizes in a reasonable computational time. However, finding the optimal tradeoff between the two approaches above will be a subject of future work.