Introduction

Owing to the richness of their intrinsic properties, transition metal oxides can bring novel functionalities to modern electronics. Recent technical advances in the fabrication of atomically abrupt oxide interface enable the formation of high mobility two-dimensional electron gases (2DEG) and trigger intense research of unusual electronic properties in deliberately designed oxide structures1,2,3,4,5. In particular, the emerging phenomena of metal-insulator transition and quantum Hall ferromagnet have been observed in a diluted ZnMgO/ZnO strongly correlated 2DEG1,6. Of interest to high frequency device application, it is essential to dilute the carrier density in device channel because that the build-up of non-equilibrium polar optical phonons will limit the high-field velocity of carriers in high density 2DEG. It is also expected that the reduction of charge carrier density will further increase the correlation effects, resulting in enhancements of the electron mass and spin susceptibility1. Spreading carriers into a wide compositionally graded heterostructure is an effective mean to dilute the carrier density, as demonstrated in the graded AlGaN/GaN and graded AlGaAs/GaAs wide parabolic quantum wells7,8,9. Such a low density three-dimensional (3D) electron slab is also a ubiquitous paradigm in solid-state physics and quantum chemistry10. If the spin degree of freedom is incorporated, spin physics as a new frontier will offer more intriguing studies in spintronics. It is also promising to develop novel spintronic devices by utilizing the desirable spin-polarization feature of high mobility electron system11. Recently, the compositionally graded ZnMgO structures have been utilized to reduce the internal electric field of quantum wells and enhance the surface Schottky barrier12,13. Here, we explore the polarization effects in a functionally graded pseudomorphic ZnMgO/ZnO heterostructure. By tailoring the bandgap and polarization effects, a diluted three-dimensional electron slab (3DES) can be achieved without compromising the high mobility characteristics. The intriguing phenomena of spin-polarization and carrier-mediated ferromagnetism in such a strongly correlated electron system have been investigated. The formation mechanism and quantum transport of 3DES are examined in terms of band structure and polarization effect.

Results

Tailoring the polarization effects in functionally graded polar oxides

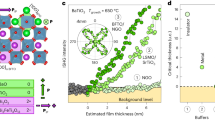
A compositional grading feature in ZnMgO layer will result in a non-vanishing divergence of polarization. It is well understood from the theory of dipole engineering established by D. Jena et al7,8,14. Figure 1 (a) shows the polarization field in the [0001] direction for a linearly graded ZnMgO/ZnO heterostructure studied in this work. The distribution of polarization dipoles and the resultant carriers are depicted schematically in Figure 1 (b) and (c), respectively. For a compressively strained ZnMgO layer, both spontaneous polarization and piezoelectric polarization should be taken into account while in a completely relaxed thick ZnO underlayer, the spontaneous polarization is only considered. In Fig. 1 (b), each unit cell is assumed to contain a charge dipole due to spatial separation of centroids of the electron clouds and the nuclei. The dipoles sheets in each unit cell neutralize each other in bulk ZnO. However, the strength of the dipole changes with increasing Mg composition, breaking the local charge neutrality in the ZnMgO layer. To visualize the microscopic landscape of polarization effect, we divide the Zn1−xMgxO layer into N unit cells with a Mg composition linearly increasing from the interface (z = z0) to the top surface (z = 0). The unit number N is equal to d/c, where d is the thickness of graded layer and c is the length of a unit cell. For the ith unit cell, Mg composition is and the unbalanced bound sheet charge is equal to and at the upper and lower surface, respectively. Due to the gradient polarization discontinuity 4, the unbalanced net bound charges are positive with its sheet density of at the interface between the ith and (i+1)th unit cells. As a result, the bound positive polarization charges are spread throughout the linearly graded layer with a volume density of 7. Consequently, these fixed positive charges will attract mobile electrons to satisfy the Poisson's equation and local charge neutrality in the bulk. Thus, gradient polarization magnitude introduces a three-dimensional mobile electron slab (3DES).

Figure 1
figure 1

(a) Polarization field directions, (b) schematic distribution of polarization dipole and (c) distribution of resultant carriers in the linearly graded ZnMgO/ZnO heterostructure in the [0001] orientation.

PSP and PPB represent the spontaneous and piezoelectric polarizations, respectively. The parameter c is the lattice constant, σπ is the polarization-induced charges on top of the surface and NDπ is the sheet density of positive unbalanced polarization charges.

Full size image

Composition gradient in ZnMgO/ZnO heterostructure

In this work, the polarization gradient is experimentally realized by utilizing the compositional pulling effect in ZnMgO/ZnO heterostructure grown on sapphire under thermal equilibrium conditions by metal-organic vapor phase epitaxy (MOVPE) technique15. The details are given in the Method section. The single heterostructure (sample A) consists of a Zn1−xMgxO (75 nm) on ZnO template with x = 0.18 at the topmost surface, while the double heterostructure (sample B) has a sandwich feature: graded-Zn0.8Mg0.2O (60 nm)/ZnO (30 nm)/graded-Zn0.85Mg0.15O (90 nm). Figure 2 (a) shows a cross-sectional image of sample B obtained by high-angle annular dark-field cross-sectional scanning transmission electron microscopy. The sandwiched ZnO layer appears as bright because the heavier Zn2+ ions appear brighter than the Mg2+ ions. The atomic lattice in both ZnMgO and ZnO layers is clearly seen (right enlarged image in Fig. 2 (a)), indicative of state-of-the-art epitaxial heterostructure formed. Fig. 2 (b) shows energy-dispersive X-ray (EDX) chemical maps of Mg and Zn and as well as monochromated low-loss electron energy-loss spectroscopy (EELS) data. The contrast in the maps illustrates the composition distribution of Zn and Mg in the heterostructure and the spatially resolved EELS spectra exhibit a stepwise absorption feature resulting from the electronic bandgap onset. The EELS spectra are displayed at 5 nm intervals, with ZnO region as marked by red lines. The extracted bandgap profile at the right of Fig. 2 (b) was taken from all 1nm-spaced EELS spectra. The profile shows a linear bandgap-energy reduction, which is consistent with the Zn and Mg distributions of ZnMgO layers. This indicates that the gradient distribution of Mg in ZnMgO layers has been achieved. This compositional gradient phenomenon in ZnMgO layer is known as compositional pulling or lattice latching effect, which is related to the misfit strain in the films16,17. From the viewpoint of thermodynamics, the biaxial compressive strain will pull the Mg adatoms from the growing front surface of ZnMgO in the initial stage to reduce the deformation energy. As growth continues, a graded strain reduction allows the subsequent deposition of a ZnMgO layer with high x. Due to the gradual distribution of strain throughout the whole ZnMgO layer and not accumulated at the sharp interface, the ZnMgO layer can grow coherently in the critical range without generating new misfit dislocations. The slope of grading can be tuned by various thermodynamic growth conditions such as temperature and Mg/Zn gas-phase mole ratio18.

Figure 2
figure 2

(a) Cross-sectional STEM HAADF image and the corresponding higher magnification image of the boxed region; (b) (left to right) EDX chemical maps with projected Mg and Zn, monochromated low-loss EELS spectra and the extracted bandgap energy profile of ZnMgO/ZnO/ZnMgO double heterostructures (sample B).

Full size image

Strain evolution and polarity stabilization in graded ZnMgO layer

The piezoelectric polarization field is sensitive to the strain evolution in graded ZnMgO layer, which can be examined by means of high resolution x-ray diffraction. Figure 3 (a) and (b) illustrate the reciprocal-space maps (RSMs) recorded in the vicinity of (105) asymmetric reflection of ZnMgO/ZnO heterostructures of sample A and B, respectively. In both samples, identical reciprocal coordinate qx are obtained for both ZnMgO and ZnO template which indicate that ZnMgO barrier layers are coherently strained to the underlying ZnO layers. The lattice constant of the pseudomorphic ZnMgO barrier along the c-axis decreases less gradually than the relaxed films, suggesting that the alloying barriers suffer from the in-plane compressive (out-of-plane tensile) strain19. The elongated and broadened reciprocal lattice point of ZnMgO along qz vector indicates a gradual decrease of the lattice constant along c-axis, clearly exhibiting the presence of Mg composition gradient.

Figure 3
figure 3

(105) asymmetric RSMs of sample A (a) and sample B (b).

Full size image

We employed X-ray photoemission spectroscopy (XPS) to probe the chemical and electronic nature of ZnMgO surface. The shape of valence band (VB) XPS in Figure 4 (a) clearly exhibits Zn-polarity, in which O 2p valence band states are distinguished20. It is known that ZnMgO epilayers exhibit higher spontaneous polarization effects than ZnO. Due to large electronegativity of oxygen, the polar surfaces are electrostatically unstable and the surface reconstruction or hydroxide absorption is considered crucial to stabilize the polar surface21,22,23. In checking for O 1s core-level spectrum, only one dominant peak at 531.00 eV was observed in Fig. 4(b) due to oxygen in the bulk and thereby the absorbed OH groups were not obviously present in such clean surface. Thus, the surface reconstruction with formation of structural defects could be the dominant stabilization mechanism. The analysis of XPS indicates that the atomic ratio of [O]/[Zn+Mg] on Zn-polar ZnMgO epilayer is 49.70/48.84, slightly deviated from the stoichiometry. The modification of the surface stoichiometry for the stability of (0001)-Zn surface is also related to the redistribution of the surface charges through the formation of O-terminated defects. The atomic force microscopic image in Figure 4(c) exhibited the triangular jagged step edges and tiny pits were dominant on the surface graded ZnMgO layer and the mean surface roughness is only 0.42 nm over 3 µm×3 µm area. These triangular shaped features are similar to those observed by Dulub et al21, which are not present on the O-polar or nonpolar faces. In fact, during the step-flow growth under thermal equilibrium, the different growth speed is determined by different dangling bond densities at two kinds of step edges, leading to the jagged structures. The theoretical calculations and experimental results suggests that these step edges are O-terminated and thereby result in the overall decrease of the surface Zn concentration, which in turn build in a net-electric field to compensate the electrostatic surface instability21,22. On the other hand, the lattice-mismatch induced compressive strain in ZnMgO will tend to relax and give priority to the formation of tiny pits at the step edges of terraces. These pits are also considered to be clusters of negative charged Zn vacancies with O-terminated hexagonal cavities23. Therefore, the formation of structural defects Zn vacancies or even vacancy clusters are energetically favored and abundant on the surface regime.

Figure 4
figure 4

(a) The valance-band and (b) O 1s core-level x-ray photoelectron spectrum of sample A calibrated by carbon 1s (284.6 eV); (c) AFM images of (a) ZnMgO/ZnO double heterostructure (sample B).

Full size image

Polarization charge distribution and carrier profile of 3DES

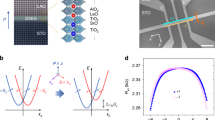
The polarization tailoring effect is verified by performing self-consistent Poisson and Schrodinger band calculations based on the surface charge model24. Figure 5 (a) and (b) show the calculated band diagrams and charge profiles at zero bias for both structures and the real carrier profiles of samples derived from capacitance-voltage (C-V) measurements. The surface potential is determined to be 1.2 eV by VB-XPS in Fig. 4 (a), where the Fermi level is located at energy level of 2.49 eV above the maximum of valence-band and the corresponding bandgap of ZnMgO on the surface is 3.69 eV. The polarization constants used in the calculation are obtained from Ref.25. Taking both the spontaneous and piezoelectric polarization effects into account, the polarization discontinuity in a coherently strained ZnMgO is expressed as PSP+PE(x) = 0.029x(C/m)26. For a linear gradient from ZnO to ZnMgO over length d with x(z) = x0z/d (x0 is the Mg composition on the topmost surface), the volume density of itinerant carriers is given as n3D = NDπ = 0.029x0/d. It is found that the calculated carrier profile coincide well with those derived from C-V profiling. As expected, mobile carriers are accumulated within the graded barrier layer with a depletion layer ddepl near the surface due to upward band bending. The resultant carrier sheet density is approximated to be n3D×(d−ddepl) with sheet density of 1.48×1012 and 3.89×1012 cm−2 for samples A and B, respectively. It is noted that the spreading widths of electron slabs are larger than the thermal de-Broglie wavelength ( at 300 K) or Fermi wavelength (λ = 2π/kF≈26 nm) for the given carrier density of n3D = 4.77×1017cm−3 in sample A. The electronic system here is therefore expected to have a 3D single particle energy spectrum and the carriers act just like bulk doped electrons but with high mobility.

Figure 5
figure 5

The calculated band diagrams and charge profiles at zero bias and carrier depth profile derived from C-V measurements for (a) sample A and (b) sample B.

Full size image

Quantum transport of spin-polarized high mobility carriers

Figure 6 shows the temperature dependent Hall effect data for both samples A and B and a ZnO template for reference. At high temperature, the differences in sheet carrier concentration and mobility are not well distinguished between heterostructures and ZnO template because the parallel conduction path served by the ZnO underlayer dominate the Hall signal. As a result, a huge deviation of ns obtained by the overall Hall data (1.16×1014 cm−2) and C-V profiling (1.48×1012 cm−2) is observed. Once at low temperature, the parallel conduction path is greatly suppressed because most of electrons are frozen onto their parent donors in ZnO underlayer and the resultant concentration decreases greatly and approaches to the real density of electron gas housed in the graded ZnMgO layer, as seen in Fig. 5 (b). We note that the parallel conduction path from ZnO underlayer is not completely suppressed and thus, the carrier concentration of 3DES determined by the Hall Effect is still overestimated while the mobility is underestimated. Alternatively, we have performed the cyclotron resonance measurements by using terahertz time-domain magneto-spectroscopy at 1.4 K. Since the terahertz conductivity is a local probe of carrier dynamics27, this may provide us more accurate information on the real 3DES. Our results show that for sample A, the carrier concentration, effective mass and mobility of the electrons are obtained to be: . We note that the carrier mobility for the polarization-doped 3DES is more than two orders of magnitude improvement as compared to undoped ZnO template. The low mobility of only 12 cm2/Vs for undoped ZnO is caused by ionized impurity scattering. While in 3DES case, the carriers spreading in a wide graded ZnMgO layer are ionized by the non-vanishing polarization field. Owing to the removal of ionized impurity scattering, no sign of electron freeze-out at low temperature is observed and thus gives rise to metallic state of 3DES with high mobility. The main limitation mechanism in 3DES is alloy disorder scattering, since the entire electron system completely resides in the graded ZnMgO layer14. As the volume density of the 3DES is diluted, the electron system can no longer fully screen the random disordered alloy potential, leading to the increased possibility of alloying disorder scattering. Furthermore, random spatial electric dipole moment due to the replacement of Zn by Mg atoms will result in a non-periodic electronic potential28, thereby enhancing the dipole scattering of mobile electrons.

Figure 6
figure 6

(a) Mobility and (b) sheet carrier concentration of ZnMgO/ZnO heterostructures (samples A and B) as well as the reference ZnO template.

Full size image

Next, we turn to the quantum transport properties of the 3DES. If ignoring the quantum electron-electron correlation effects, the 3DES investigated here has 3D Landau-level spectrum without variations of the density of states due to dimensional quantization across the spreading layer, as confirmed by CV profiling. However, below a certain temperature, the characteristic coherent length () for coherent transport is larger than the electron spreading width and thus, the system becomes 2D for coherent phenomena in the diffusive transport29 (D = vFl is the diffusion coefficient along the magnetic field, l = vFτ = 55.7 nm is the mean free path for sample A). Figure 7 shows the angular-dependent magnetoresistance (Rxx) and Hall resistance (Rxy) as a function of magnetic field for sample A. When the magnetic field is perpendicular to the sample surface (z//B,θ = 00 where z is the growth direction), the structure of Rxx and Rxy resemble the Shubnikov-de Haas (SdH) oscillation and quantum Hall effect (QHE) for a 2D electron system. Above ~3 T, well-resolved SdH oscillations and quantum Hall plateaus are observed and the minima of ρxx coincide well with the quantized Hall resistivity (ρxy) plateaus of h/(vq2), where v is the Landau filling index. However, compared to the conventional QHE in 2DEG, neither the steps of Rxy plateaus are completely flat nor the minima of Rxx are very deep. This is due to the energy gap that is not yet fully developed in a finite magnetic field27. The negative parabolic magnetoresistance characteristic is observed at low field. It is related to the weak localization and electron-electron interaction effects, which only occur in the coherent diffusive transport regime30. By rotating the magnetic field away from the perpendicular orientation, the minima in Rxx are strongly suppressed. With the magnetic field parallel to the sample surface (), the SdH oscillation can still be observed to start with an onset at higher field, which unambiguously implies the quantization of three-dimensional bulk Fermi surface. However, the in-plane oscillation amplitude decreased greatly, which could be ascribed to the finite ratio of the electron spreading width with respect to the magnetic length (). The similar features of SdH oscillations under in-plane magnetic field have also been observed in AlGaAs/GaAs wide parabolic quantum well and heavily doped GaAs layer29,31.

Figure 7
figure 7

(a) Angular-dependent normalized magnetoresistance Rxx/R0 versus B and Hall resistivity Rxy of sample A as a function of magnetic field (z//B, θ = 0°) at 1.4 K; (b) FFT power spectrum of Rxx versus B at 1.4 K.

Full size image

The theoretical expression of the envelope function of the SdH oscillation in 3D case can be given as31

Where , is the Fermi energies of 3D states, is the cyclotron frequency, m is the electron effective mass, τ is the quantum scattering time and R0 represents the classical resistance in zero magnetic fields. When the high mobility system is at extreme low temperature of 1.4 K, the magnetoresistance exhibited a weakly modulated (~B1/2) dependence of and the period of the oscillatory cosine term yields the carrier density. We employed the standard Fast Fourier Transform (FFT) method to extract the periodicity of SdH oscillatory component and the FFT power spectrum is shown in Fig. 7 (b). Two peaks are clearly resolved with their locations at f1 = 51.92 T and f2 = 19.26 T, together with a shoulder peak on the left side of f1 peak. The peak fitting result indicates that the shoulder peak is superimposed by the second harmonic peak 2f2 and the dominant peak f1. If we assume that the two FFT peaks arise from the population of two subbands, the sheet carrier concentration is then given as , while if considering the spin-polarized Fermi surface, the value is . The latter value agrees well with the concentrations derived by means of capacitance-voltage (1.48×1012 cm−2 at RT) as well as cyclotron resonance (1.8×1012 cm−2 at 1.4 K). Thus, the resultant volume carrier concentration (n3d) is calculated be 4.77×1017 cm−3. Correspondingly, we can conclude that such diluted 3DES are partially spin polarized with spin polarization degree ) of 0.46 and a large zero-field spin-splitting energy of 11.5 meV. Here and are the spin-up and spin-down carrier densities and .

Discussion

In the framework of Landau's Fermi liquid approach, the carrier-carrier interaction effects can be described using a dimensionless Wigner-Seitz parameter rs, which is defined as the ratio of Coulomb interaction to Fermi energy. The rs value has a strong dependence on carrier concentration with the relationship given as in 3D case32. Here, aB = (ε/mb)ab = 1.54 nm, which gives the effective Bohr radius with dielectric constant of ε = 8.45 and effective mass of conduction-band electron (mb = 0.29me). Given the volume carrier concentration of , rs in sample A is 6.25. We note that it is rather difficult to achieve high rs value while still maintaining a high mobility in other semiconductor materials. Due to very small lattice mismatch, the pseudomorphic growth of Zn0.8Mg0.2O on ZnO can be achieved with critical thickness up to 700 nm19. Thus, it is possible to further tune down the gradient of Mg composition in a wider thickness range and the polarization-induced charge density of high mobility 3DES can be diluted lower than 1016 cm−3. In this situation, the corresponding value of rs>22 can be reached and new physics such as metal-insulator transition or even quantum Hall ferromagnetic states can possibly be observed.

Knowing the interaction effects of carriers in diluted 3DES, we can now re-examine the feature of huge spin splitting energy of 11.5 meV in such intrinsic ZnMgO/ZnO system. The well-known Rashba spin-orbital coupling (SOC) effect due to inversion asymmetry are usually responsible for the zero-spin splitting phenomenon observed in AlGaAs/GaAs material systems. However, the SOC coefficient is very small in ZnO (about 1.1 meV Å)33 and thus, it cannot explain our result. In fact, as the magnetic field is applied parallel to the surface of sample A, the Lorenz force and weak localization due to orbital effects are eliminated and the distinct negative magnetoresistance is observed. This strongly suggests the inherent magnetic order of 3DES34. The scenario of magnetic impurity induced spin-polarization can be ruled out because no magnetic impurities are detected by SIMS measurement within its detection sensitivity. Thus, the spin polarization observed in the magneto-transport is due to the ferromagnetic phase of electrons in 3DES, similar to the observations in 2DEG confined in non-magnetic polar oxides (LaAlO3/SrTiO3) heterostructures35. Theoretical study has predicted an itinerant 3DES will undergo a transition to a ferromagnetic phase in the limit of a large ratio of Columbic to kinetic energy (rs> 50)36. By comparison, rs for 3DES investigated here is not large enough to induce the quantum Hall ferromagnetic phase and therefore, we infer that the spin polarization is originated not only from the intrinsic electron-electron interaction but also includes other effects.

Figure 8(a) shows the magnetic hysteresis loops of sample A and ZnO template measured at 5 K after diamagnetic and paramagnetic subtraction. The sample A exhibits an enhanced ferromagnetism (FM) as compared to the ZnO template and the remanent moment at zero field is 2×10−6 emu/cm2 after subtracting the contribution from ZnO template. We determine the net spin polarized electrons by adding the net moments of all dipoles in 3DES, yielding (μB is the Bohr magneton). The net magnetic moment induced by delocalized electrons in 3DES is estimated to be three orders of magnitude lower than the zero-field remanent moment of 1.8×1014 μB cm−2 measured by SQUID. Such a difference is also observed in LaAlO3/SrTiO3 system37. It implied that the host ferromagnetism does not allow spin manipulation and the vast majority of localized spins have no contribution to the transport properties.

Figure 8
figure 8

(a) The M-H loop after diamagnetic and paramagnetic subtraction for sample A and referenced ZnO template measured at 5 K; (b) zero-field cooled (ZFC) and field-cooled (FC) magnetization curves of sample A.

Full size image

So far, the issue of intrinsic ferromagnetism in nonmagnetic oxides nanostructures and thin films is still controversial. Nonetheless, most of the recent reports indicate that the main source of the magnetic moment is likely due to the unpaired 2p electrons at oxygen site surrounding the Zn vacancies and vacancy-vacancy interaction in the ground state will enhance the magnetic moments38. Our XPS and AFM results imply that Zn vacancies are expected to be majority of structrual defects at surface regime driven by the polarity stablization and strain relaxation mechanisms. The theoretical calculation predicted that the surface ferromagnetism in polar ZnO surface is in turn a plausible general stablization mechansim of polar ionic surfaces39. Since Zn vacancies amount are less in the bulk and do not lead to magnetism because of their stronger orbital hybridizations, we believe that Zn vacancies at the surface regime is most likely the main source of ferromagnetism. This also agrees with various observations of enhanced ferromagnetism in nanostructured and ultra-thin films in which materials are non-magnetic but exhibit high surface-volume ratio38. It was also well supported by the fact that the ferromagnetism is enhanced with the increasing of ZnMgO thickness and Mg composition in a series of controlled samples that we have investigated (see Supporting Information ).

Figure 8 (b) shows the zero-field cooled (ZFC) and field cooled (FC) magnetization as a function of temperature for sample A. The measurement was carried out while warming the sample from 5 to 300 K using a small applied magnetic field (100 Oe). The magnetization decreases quickly till 90 K and remains weak up to 300 K. The magnitude and temperature dependence of the magnetic response in ZFC and FC curves indicated that the vast majority of the carriers are localized at the surface local moments. Although the valence electrons in O 2p orbitals are less delocalized than those in d or f orbitals in transition metals38, large thermal energy is necessary to activate the electrons localized in such deep level Zn vacancies. Thus, at extreme low temperature, these localized spins are immobile and have no contribution to the transport properties. However, driven by the non-vanishing polarization field across the graded ZnMgO layer, a small fraction of carriers at the surface regime above the Fermi level are migrated and transferred into the conduction band to form 3DES, similar to the transfer process of 2DEG at the LaAlO3/ SrTiO3 and ZnMgO/ZnO interface26,40. In this region visited by the itinerant carriers the ferromagnetic exchange interactions are strong via coupling to the surface local moments. The large coherent length and mean free path of electrons also ensure low possibility of spin-flip during carrier migration, thus giving rise to the spin-polarization feature. Note that although rs in 3DES is not high enough for ferromagnetic phase transition, the diluted electron density definitely favors the spin polarization phenomenon. This is also consistent with small spin polarization degree of 0.35 for the 2DEG confined in ZnMgO/ZnO sharp interface with same Mg composition of x = 0.1815. Additionally, as the magnetization originates mainly from the surface regime, the interplay of surface charges and spins with the absorbed charged species is expected to be strong and thus, the ZnO-based open gate transistor can be utilized for biocompatible medicinal applications.

In summary, we have demonstrated the tailoring of polarization effects in functionally graded polar oxides to produce high mobility 3DES without impurity doping. The ability to tune carrier density in graded ZnMgO/ZnO heterostructure provides the opportunity to explore strong correlation effects in the area of quantum transport and spintronics. The important feature of spin polarization is the result of exchanging interaction of itinerant electrons and vacancies induced local magnetic moments. The enhanced correlation effects in such diluted electron system will facilitate the spin polarization and thus, it could benefit novel all-oxide electronic and spintronic devices for high-field operation.

Methods

Sample growth

ZnMgO/ZnO heterostructures were grown on sapphire (0001) substrates using the Aixtron close-coupled showerhead (CCS) MOVPE system13. Dimethylzinc (DMZn) and bis(methlycyclopentadienyl) magnesium (MeCp2Mg) were used as the Zn and Mg sources, respectively. We used N2O as the oxygen source and N2 as the carrier gas. A 0.4 µm-thick ZnO buffer layer was deposited at 450°C, followed by a 3.3 µm undoped ZnO layer and an undoped ZnMgO layer, both grown at 920°C. The ZnO template exhibited a Zn-face polarity with excellent crystal quality and layer-by-layer surface morphology. The values of full-width at half maxima (FWHM) of the ω-scan rocking curves from both symmetric (0002) and asymmetric planes are 186 and 622 arcsec, respectively. It clearly indicates the state-of-the-art quality of the ZnO films with low dislocation density despite of large lattice mismatch (18%) between ZnO and sapphire. The Mg content (x) in ZnMgO layer was determined from the reflectance measurement of the bandgap energy of Zn1-xMgxO and using the equation Eg(x) = Eg(0)+2.145x26.

Sample characterization

The surface morphology was characterized by the atomic force microscopy (Nanoscope IIIa, Digital Instruments Inc.) working in the tapping mode and high resolution x-ray diffraction (HRXRD) was performed on a Panalytical MRD diffractometer equipped with a position sensitive detector placed on the 2θ arm. The Cu radiation was selected by a flat Ge (444) monochromator. Capacitance-voltage (C-V) measurement was performed using mercury contacts at frequency of 1 MHz. Nanoscale analysis was carried out with a monochromated FEI Titan scanning transmission electron microscope (STEM) operated at 300 kV. Energy-dispersive X-ray (EDX) analysis was performed using an electron probe with a relatively large diameter of 0.5 nm to increase the spectral counts. Electron energy-loss spectroscopy (EELS) was further utilized to probe the band structure of the heterostructure using a monochrome STEM probe with a diameter of about 1 nm. The energy resolution of the measurement was better than 0.13 eV and the corrections of bandgap, composition and profiling depth are the same as discussed earlier41. Temperature-dependent Hall measurements were carried out at low magnetic field of ~1 T and temperature ranging from 10 to 300 K. Quantum transport properties were measured in a rotator-equipped Oxford refrigerator at 1.4 K with the magnetic field up to 10 T. The field-dependent Hall effect was performed at 10 K for sample A with B field up to 1.4 T. by using the Lakeshore commercial Hall effect system 7707A. Both Hall effect and magnetotransport measurements are performed in a van der Pauw geometry using indium as the ohmic contact metal. The magnetic properties of sample A and ZnO template were measured using superconducting quantum interference devices magnetometry (SQUID) at 5 K. XPS measurements were performed using a Kratos Ultra DLD spectrometer and monochromated Al Kα radiation. The atomic concentrations of each element were determined from the areas of the Zn 2p, Mg 1s, O 1s and C 1s core-level peaks using sensitivity factors based on spectrometer-modified Scofield cross-sections.