Abstract
A gas of magnons in magnetic films differs from all other known systems demonstrating Bose-Einstein condensation (BEC), since it possesses two energetically degenerate lowest-energy quantum states with non-zero wave vectors ±kBEC. Therefore, BEC in this system results in a spontaneously formed two-component Bose-Einstein condensate described by a linear combination of two spatially non-uniform wave-functions ∝exp(±ikBECz), while condensates found in other physical systems are characterized by spatially uniform wave-functions. Here we report a study of BEC of magnons with sub-micrometer spatial resolution. We experimentally confirm the existence of the two wave-functions and show that their interference results in a non-uniform ground state of the condensate with the density oscillating in space. Additionally, we observe stable topological defects in the condensate. By comparing the experimental results with predictions of a theoretical model based on the Ginzburg-Landau equation, we identify these defects as quantized vortices.
Similar content being viewed by others
Introduction
Bose-Einstein condensation (BEC), predicted by Einstein1 in 1925, is one of the most intriguing quantum phenomena, since it allows one to observe coherent quantum effects on the macroscopic scale (for review see, e.g.,2). Although BEC was experimentally observed for different equilibrium (liquid He4 3,4, ultra-cold atoms5,6, magnetic triplons7) as well as non-equilibrium (excitons8, polaritons9,10,11, magnons12,13, photons14) ensembles of bosonic particles, the experimental investigation of spatially coherent structures in BECs remains an attractive albeit a challenging task for researchers. The most unambiguous way to investigate spatial coherence of a BEC is an interference experiment. For atomic condensates this can be done by splitting the condensate cloud into two parts and bringing them to spatially overlap after their phases or wave vectors have been manipulated independently15. Quasi-equilibrium BEC of magnons in ferromagnetic films13 differs from all other BEC systems. Since the lowest-energy magnon state is doubly degenerate, the condensation spontaneously occurs at two non-zero values of the wave vector k = ±kBEC. This leads to a degeneracy of the condensate ground state and coexistence of two spatially overlapping wave-functions ψ+ and ψ−, that correspond to ±kBEC. The structure of these wave-functions, including the information about their relative phases, can be probed by a visualization of the density of the total wave-function  . Below we show experimentally that the coexistence of these two intrinsic components results in the formation of a non-uniform ground state of the magnon condensate, characterized by a real-space standing wave of the condensate density. This observation provides a direct evidence of the spatial coherence in the room-temperature magnon condensate. Note that contrary to the interference experiments with cold atoms, where condensates with different wave vectors were prepared by external manipulation15, in our experiments the two interfering condensate components are formed spontaneously.
. Below we show experimentally that the coexistence of these two intrinsic components results in the formation of a non-uniform ground state of the magnon condensate, characterized by a real-space standing wave of the condensate density. This observation provides a direct evidence of the spatial coherence in the room-temperature magnon condensate. Note that contrary to the interference experiments with cold atoms, where condensates with different wave vectors were prepared by external manipulation15, in our experiments the two interfering condensate components are formed spontaneously.
Due to the spatial coherence, both equilibrium and non-equilibrium BEC systems can demonstrate macroscopic topological structures such as quantized vortices. However, the role of gain and dissipation in the formation of structures is essentially different in these two cases. In equilibrium condensates, e.g. condensates in ultra-cold gases, vortices are created either during the condensate formation16,17 or via dynamical perturbations18,19. Unless the perturbations are constantly maintained, the vortices leave the condensate, while the condensate relaxes into its ground state. In this case, the existence of perturbations is necessary for the formation of topological structures, but it is not a precondition for the existence of the condensate itself. In contrast, non-equilibrium condensates, such as magnon condensates, are created under the continuous influence of an external force as a result of the balance between gain and losses. Such systems can spontaneously form stationary or dynamical vortex structures (see20 for details), that would not exist in equilibrium condensates.
Recently, stationary vortices and half-vortices pinned at the local minima of the energy landscape have been observed in exciton-polariton condensates21,22. The vortices in these experiments were created dynamically due to the difference in energy level between minima and maxima of the landscape that explains why the vortices of the same orientation at the same position appear for different experimental realizations. It remained unclear, however, whether vortices can be formed during condensation in other non-equilibrium condensates. Here we show that, indeed, stationary quantized vortices exhibiting a number of unique features can be spontaneously formed in a condensate of magnons created in epitaxial magnetic films of exceptionally high crystallographic quality.
Results
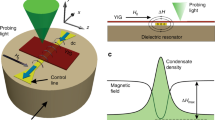
A room-temperature Bose-Einstein condensate of magnons was created in an epitaxial yttrium iron garnet (YIG) film using an experimental setup shown in Fig. 1a, which, in general, is similar to that used in our previous studies13,23. To reach the critical value of the chemical potential, necessary for BEC formation24, we inject additional magnons using microwave parametric pumping. After thermalization, the injected magnons gather in the two lowest-energy states and create a degenerate two-component Bose-Einstein condensate, as illustrated in Fig. 1b.
Schematic of the experiment and results of two-dimensional imaging of the condensate density.
(a) Experimental setup. Magnons are injected into the YIG film using a microwave resonator. After thermalization they create a Bose-Einstein condensate, which is imaged by scanning the probing laser light in two lateral directions. (b) Qualitative picture of the magnon spectrum in a ferromagnetic film. Injected magnons thermalize and create two Bose-Einstein condensates at two degenerate spectral minima with non-zero wave vectors ±kBEC. (c) Measured two-dimensional spatial map of the BLS intensity proportional to the condensate density, obtained at the maximum used pumping power. Dashed circles show the positions of topological defects in the standing-wave pattern corresponding to a non-uniform ground state of the condensate. (d) Two-dimensional Fourier transform of the measured spatial map. Dashed line marks the value of the wave vector equal to 2kBEC. The spread of the spectral peak and its slight displacement with respect to ky = 0 are caused by the presence of topological defects resulting in a non-zero slope of the real-space stripe structure, as well as by slight misalignment between the static magnetic field and the scanning axis.
Spatial mapping of the total condensate density was performed using micro-focus Brillouin light scattering (BLS) technique25. The locally detected BLS intensity is proportional to the squared amplitude of the magnetization precession, i.e. to the total condensate density  at the point of observation. Therefore, by scanning the probing laser spot in the two lateral directions and recording the BLS intensity, spatial distribution of the condensate density can be visualized.
at the point of observation. Therefore, by scanning the probing laser spot in the two lateral directions and recording the BLS intensity, spatial distribution of the condensate density can be visualized.
Figure 1c shows the results of a two-dimensional mapping of the condensate density across an 8×5 µm2 area of the YIG film adjacent to the pumping resonator, within which the field created by the resonator can be considered as being approximately uniform. The mapping was performed by repetitive scanning of the spatial area followed by the averaging of the recorded data to improve the signal-to-noise ratio. The map clearly demonstrates a periodic pattern along the direction of the static magnetic field created as a result of interference of the two components of the magnon condensate. The spatial period of the pattern 0.9±0.1 µm obtained from two-dimensional Fourier transform of the recorded map (Fig. 1d), agrees well with the period 0.92 µm calculated based on the known value kBEC = 3.4×104 cm−1 26. The depth of the periodic spatial modulation was far below 100% and was found to depend on the pumping power, as illustrated by Fig. 2. As seen from these data, the average BLS intensity proportional to the total density of the condensate gradually grows with pumping power increasing from the BEC-transition threshold of 6 mW to 100 mW and then saturates due to the reduction of the parametric pumping efficiency27. In contrast, the modulation depth increases quickly at powers just above the threshold and then stays nearly constant.
Effect of the pumping power on the condensate density and on the amplitude of the standing wave.
Filled symbols show the average BLS intensity proportional to the total density of the condensate. Open symbols show the relative depth of the spatial modulation of the BLS intensity, which characterizes the strength of the phase locking between the condensate components. The data were obtained from one-dimensional scans parallel to the direction of the static field. Lines are guides for the eye.
Another interesting feature of the interference pattern in Fig. 1c is the presence of topological defects marked by dashed circles. These defects correspond to singularities of the phase difference between the individual components ψ+ and ψ−. To illustrate this, we draw contours around the defects and calculate the phase shift over them. It is obvious that the phase difference is constant as one moves along a red or dark blue line in the map and that the phase changes by 2π, as one moves from a red (blue) line to the neighboring one. When calculating the phase shift over the shown contours according to these rules, one gets 2π in either ψ+ or ψ− for both defects.
Discussion
The detected periodic modulation of the condensate density clearly confirms the existence of two spatially coherent wave-functions in the magnon condensate. Moreover, the observation of the pattern in the long-term repetitive measurements clearly shows that the two components of the condensate are phase locked. If this were not the case, the fluctuations of the phase difference between the wave-functions ψ+ and ψ− would lead to changes in the spatial positions of the maxima and minima in the pattern with time. As a result, the pattern would be washed out due to the averaging during the long-term measurements. We associate this phase locking with interaction of magnons belonging to the two condensate components resulting in their phase coherence. We emphasize that, only a small part (about 1%) of total number of magnons is condensed at room temperature24. Therefore, the dominating interaction of the condensed magnons with the non-condensed magnons reduces the strength of the phase locking between the two components of the condensate. The same arguments explain the increase of the modulation depth with increasing condensate density (Fig. 2).
To understand the physical origin of the observed periodic patterns and topological defects and the role of the phase locking between the two condensate components for their formation, we model the condensate using two coupled generalized Ginzburg-Landau equations following the approach previously applied to non-equilibrium condensates in28,29,30. Interactions between condensate components are taken into account by introducing additional terms describing four-magnon interaction processes31,32 that destroy a pair of non-condensed magnons and create a pair of magnons with wave vectors ±kBEC and vice versa. The resulting system of coupled equations for wave-functions ψ+ and ψ− becomes

Here U0 is the strengths of the pseudo-potentials responsible for self-interaction (we neglect the cross-interaction between the components),  and
and  are the longitudinal and transverse masses of magnons, respectively, with me being the free electron mass. P(ψ±) describes the flow of magnons into the condensate due to the parametric pumping and their annihilation due to magnon-magnon interactions and spin-lattice relaxation. Based on the approach from28,29, P(ψ±) can be written phenomenologically as
are the longitudinal and transverse masses of magnons, respectively, with me being the free electron mass. P(ψ±) describes the flow of magnons into the condensate due to the parametric pumping and their annihilation due to magnon-magnon interactions and spin-lattice relaxation. Based on the approach from28,29, P(ψ±) can be written phenomenologically as  , providing the simplest form of a saturating gain. Here γeff is an effective gain, that takes into account both the pumping and the linear annihilation of magnons, η describes the energy relaxation via interactions of the condensate with non-condensed magnons and Γ describes the nonlinear reduction of the pumping efficiency at large magnon densities. The last term in Eq. (1) is responsible for the phase locking between ψ+ and ψ−.
, providing the simplest form of a saturating gain. Here γeff is an effective gain, that takes into account both the pumping and the linear annihilation of magnons, η describes the energy relaxation via interactions of the condensate with non-condensed magnons and Γ describes the nonlinear reduction of the pumping efficiency at large magnon densities. The last term in Eq. (1) is responsible for the phase locking between ψ+ and ψ−.
Epitaxial YIG films possess exceptionally high crystallographic quality with a remarkably low number of crystalline defects33. However, these defects play a decisive role in the pinning of topological structures in the magnon condensate. In a non-equilibrium system there always exist velocity fluxes connecting regions where the particles are created to the regions where they are annihilated. Therefore, topological structures such as vortices and solitary waves are stationary only, if they are pinned by forces counteracting the flow drag. To model the effect of the crystalline defects, we shall assume that in a certain region of the sample there exist some localized areas causing an additional annihilation of magnons within an area with characteristic lateral sizes equal to the healing lengths  μm. We model this increase by a spatially dependent
μm. We model this increase by a spatially dependent  defined as
defined as  outside the defect area and
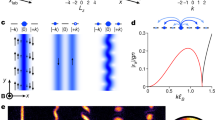
outside the defect area and  inside the defect area. According to the scenario of BEC elucidated in34 the non-condensed thermal magnons evolve into a quasi-condensate with many quantized vortices before relaxing to the genuine vortex-free condensate state. In the presence of the pinning defects the vortices formed in their vicinity can be pinned to them. We have verified this scenario by a direct numerical integration of Eq. (1) starting from random initial configurations for ψ+ and ψ− in the presence of two defects located 3 μm away from each other. In the simulations we observed several possible stationary vortex configurations: only one component of the condensate had a vortex pinned to one of the defects, each component had one vortex and these two vortices were pinned either to the same defect or to different defects. The latter case is apparently realized in the experiment, as corroborated by the striking similarity between Fig. 1c and Fig. 3 showing a pseudocolor plot of the density of the steady wave-function
inside the defect area. According to the scenario of BEC elucidated in34 the non-condensed thermal magnons evolve into a quasi-condensate with many quantized vortices before relaxing to the genuine vortex-free condensate state. In the presence of the pinning defects the vortices formed in their vicinity can be pinned to them. We have verified this scenario by a direct numerical integration of Eq. (1) starting from random initial configurations for ψ+ and ψ− in the presence of two defects located 3 μm away from each other. In the simulations we observed several possible stationary vortex configurations: only one component of the condensate had a vortex pinned to one of the defects, each component had one vortex and these two vortices were pinned either to the same defect or to different defects. The latter case is apparently realized in the experiment, as corroborated by the striking similarity between Fig. 1c and Fig. 3 showing a pseudocolor plot of the density of the steady wave-function  , obtained for this configuration by numerical integration of Eq. (1) for γeff = μC, η = 0.1 and J = 0.1μC. In addition to the interference pattern demonstrating phase locking between ψ+ and ψ−, one clearly sees in Fig. 3 two forks corresponding to the 2π shift of the phase difference between ψ+ and ψ−. These forks mark two vortices, each of them existing in one condensate component only. These structures are analogous to half vortices (fractional vortices) of two-component atomic BECs created by phase imprinting35.
, obtained for this configuration by numerical integration of Eq. (1) for γeff = μC, η = 0.1 and J = 0.1μC. In addition to the interference pattern demonstrating phase locking between ψ+ and ψ−, one clearly sees in Fig. 3 two forks corresponding to the 2π shift of the phase difference between ψ+ and ψ−. These forks mark two vortices, each of them existing in one condensate component only. These structures are analogous to half vortices (fractional vortices) of two-component atomic BECs created by phase imprinting35.
In agreement with the above arguments and the scenario of Ref.34, the patterns observed in experiments were rather stable. This was proven by performing numerous linear scans at different pumping powers switching the power on and off. These measurements have shown that the positions of the stripes in the patterns stay unchanged, although sometimes a phase shift of π was detected. This indicates that the vortex positions do not change from measurement to measurement, while their circulation connected with the orientation of the forks can be reversed. Several additional two-dimensional scans also confirmed the stability of the vortex positions. These experimental findings illustrate the important role of defects in formation of the interference pattern and vortices. The fact that the vortices can change the direction of their circulation in different realizations indicates that unlike the vortices and half-vortices found in other non-equilibrium condensates21,22, the vortices we observed are formed spontaneously during condensation and not through the dynamical interaction of fluxes. Such spontaneous formation of vortices during the condensation has been previously experimentally observed in equilibrium condensates17.
Our findings show that the room-temperature Bose-Einstein condensate of magnons represents a unique system for experimental investigations of macroscopic quantum coherence. Caused by the double-degeneracy of the lowest-energy magnon state and the presence of nonlinear magnon-magnon interactions, the ground state of the condensate appears as a real-space standing wave of the total condensate density originating from the interference of the condensate components. Apart from revealing an uncommon ground state of the Bose-Einstein condensate, this interference enables an easy observation and clear identification of complex topological structures, such as quantized vortices.
Methods
To study BEC of magnons, a 5.1 µm thick epitaxial yttrium iron garnet (Y3Fe2(FeO4)3,YIG) film with lateral dimensions 2×4 mm2 is placed into a static magnetic field H0 = 100 mT. YIG films are characterized by very small magnetic losses providing a long magnon lifetime, which appears to be much longer than the characteristic time of magnon-magnon interaction. This relation is a necessary precondition for the Bose-Einstein condensation in a gas of quasiparticles whose number is not exactly conserved20. To reach the critical value of the chemical potential, μC = 1.5×10−2 meV, necessary for BEC24, additional magnons are injected into the system by continuous parametric pumping at 8.4 GHz using a half-wavelength microwave resonator. Such pumping creates primary magnons at 4.2 GHz with wavevectors spread over the interval 2×103–1.5×105 cm−1 26. After thermalization, the injected magnons create a Bose-Einstein condensate36. For our experimental conditions the frequency of the condensate was 2.9 GHz and was found to be independent of the spatial position. In contrast to previous studies, where a pulsed pumping was used, here the pumping was applied continuously during the entire measurement time. In contrast to the pulsed regime, where the condensate is created spontaneously during each pulse, in the case of continuous pumping, once created, the condensate exists until the pumping is switched off. This allows one to avoid non-controllable changes in the phase of the condensate from one pumping pulse to the other.
Spatial mapping of the condensate density was performed using micro-focus Brillouin light scattering (BLS) technique with a spatial resolution of about 0.55 µm. The probing laser light was focused onto the surface of the film and scanned in the two lateral directions. The light inelastically scattered from magnons was analyzed by a six-pass Fabry-Perot interferometer. A detailed description of the used BLS setup can be found elsewhere25. In general, the BLS intensity is proportional to the squared amplitude of the magnetization precession in the film. Recording the BLS signal corresponding to the frequency of the condensate, one can map the total condensate density  .
.
References
Einstein, A. Quantentheorie des einatomigen idealen Gases. Sitz. Ber. Preuss. Akad. Wiss. 1, 3–8 (1925).
Pitaevskii, L. P. & Stringari, S. Bose-Einstein condensation. International Series of Monographs on Physics 116 (Clarendon Press, 2003).
Kapitza, P. Viscosity of liquid helium below the λ-point. Nature 141, 74–74 (1938).
Allen, J. F. & Misener, A. D. Flow of liquid helium II. Nature 141, 75–75 (1938).
Anderson, M. H., Ensher, J. R., Matthews, M. R., Wieman, C. E. & Cornell, E. A. Observation of Bose-Einstein condensation in a Dilute Atomic Vapor. Science 269, 198–201 (1995).
Davis, K. B. et al. Bose–Einstein condensation in a gas of sodium atoms. Phys.Rev. Lett. 75, 3969–3973 (1995).
Giamarchi, T., Rüegg, Ch. & Tchernyschyov, O. Bose–Einstein condensation in magnetic insulators. Nature Physics 4, 198–204 (2008).
Butov, L. V., Ivanov, A. L., Imamoglu, A., Littlewood, P. B., Shashkin, A. A., Dolgopolov, V. T., Campman, K. L. & Gossard, A. C. Stimulated Scattering of Indirect Excitons in Coupled Quantum Wells: Signature of a Degenerate Bose-Gas of Excitons. Phys. Rev. Lett. 86, 5608–5611 (2001).
Kasprzak, J. et.al. Bose-Einstein condensation of exciton polaritons. Nature 443, 409–414 (2006).
Balili, R., Hartwell, V., Snoke, D., Pfeiffer, L. & West, K. Bose-Einstein Condensation of Microcavity Polaritons in a Trap. Science 316, 1007–1010 (2007).
Amo, A. et al. Collective fluid dynamics of a polariton condensate in a semiconductor microcavity. Nature 457, 291–295 (2009).
Bunkov, Yu. M. & Volovik, G. E. Bose-Einstein Condensation of Magnons in Superfluid 3He. J. Low Temp. Phys. 150, 135–144 (2008).
Demokritov, S. O., Demidov, V. E., Dzyapko, O., Melkov, G. A., Serga, A. A., Hillebrands, B. & Slavin, A. N. Bose-Einstein condensation of quasi-equilibrium magnons at room temperature under pumping. Nature 443, 430–433 (2006).
Klaers, J., Schmitt, J., Vewinger, F. & Weitz, M. Bose-Einstein condensation of photons in an optical microcavity. Nature 468, 545–548 (2010).
Andrews, M. et al. Observation of Interference Between Two Bose Condensates. Science 275, 637–641 (1997).
Pethick, C. & Smith, H. Bose-Einstein Condensation in Dilute Gases (Cambridge University Press, Cambridge, England, 2002).
Weiler, C. N., Neely, T. W., Scherer, D. R., Bradley, A. S. Davis, M. J. & Anderson B. P. Spontaneous vortices in the formation of Bose–Einstein condensates. Nature 455, 948–951 (2008).
Matthews, M. R., Anderson, B. P., Haljan, P. C., Hall, D. S., Wieman, C. E. & Cornell, E. A. Vortices in a Bose-Einstein Condensate. Phys. Rev. Lett. 83, 2498–2501 (1999).
Ginsberg, N. S., Brand, J. & Vestergaard Hau, L. Observation of Hybrid Soliton Vortex-Ring Structures in Bose-Einstein Condensates. Phys. Rev. Lett. 94, 040403 (2005).
Keeling, J. & Berloff. Spontaneous rotating vortex lattices in a pumped decaying condensate. Phys. Rev. Lett. 100, 250401(2008).
Lagoudakis, K. G., Wouters, M., Richard, M., Baas, A., Carusotto, I., André, R., Dang, Le Si & Deveaud-Plédran, B. Quantized vortices in an exciton–polariton condensate. Nature Physics 4, 706–710 (2008).
Lagoudakis, K. G., Ostatnický, T., Kavokin, A. V., Rubo, Y. G., André, R. & Deveaud-Plédran, B. Observation of Half-Quantum Vortices in an Exciton-Polariton Condensate. Science 326 974–976 (2009).
Demidov, V. E., Dzyapko, O., Demokritov, S. O., Melkov, G. A. & Slavin, A. N. Observation of Spontaneous Coherence in Bose-Einstein Condensate of Magnons. Phys. Rev. Lett. 100, 047205 (2008).
Dzyapko, O., Demidov, V., Demokritov, S., Melkov, G. & Slavin, A. Quasiequilibrium gas of magnons with a nonzero chemical potential: A way to Bose-Einstein condensation. J. Appl. Phys. 101, 09C103 (2007).
Demokritov, S. O. & Demidov, V. E. “Micro-Brillouin light scattering spectroscopy of magnetic nanostructures”. IEEE Trans. Mag. 44, 6–12 (2008).
Demidov, V. E. Dzyapko, O., Buchmeier, M., Stockhoff, T., Schmitz, G., Melkov, G. A. & Demokritov, S. O. “Magnon Kinetics and Bose-Einstein Condensation Studied in Phase Space”. Phys. Rev. Lett. 101, 257201 (2008).
Gurevich, A. G. & Melkov, G. A. Magnetization Oszillations and Waves (CRC Press, New York, 1996).
Borgh, M. O., Keeling, J. & Berloff, N. G. Spatial pattern formation and polarization dynamics of a nonequilibrium spinor polariton condensate. Phys. Rev. B. 81, 235302 (2010).
Keeling, J. & Berloff, N. G. Controllable half-vortex lattices in an incoherently pumped polariton condensate. arXiv:1102:5302.
Malomed, B. A., Dzyapko, O., Demidov, V. E. & Demokritov, S. O. Ginzburg-Landau model of Bose-Einstein condensation of magnons. Phys. Rev. Lett. 81, 024418 (2010).
Rezende, S. M. Theory of coherence in Bose-Einstein condensation phenomena in a microwave-driven interacting magnon gas. Phys. Rev. B 79, 174411 (2009).
Tupitsyn, I. S., Stamp, P. C. E. & Burin, A. L. Stability of Bose-Einstein Condensates of Hot Magnons in Yttrium Iron Garnet Films. Phys. Rev. Lett. 100, 257202 (2008).
Cherepanov, V., Kolokolov, I. & L'vov, V. The saga of YIG: spectra, thermodynamics, interaction and relaxation of magnons in a complex magnet. Phys. Rep. 229, 81–144 (1993).
Berloff, N. G. & Svistunov, B. V. Scenario of strongly nonequilibrated Bose–Einstein condensation. Phys. Rev. A 66, 013603 (2002).
Matthews, M. R., Anderson, B. P., Haljan, P. C., Hall, D. S., Wieman, C. E. & Cornell, E. A. Vortices in a Bose-Einstein Condensate. Phys. Rev. Lett. 83, 2498 (1999).
Demidov, V. E., Dzyapko, O., Demokritov, S. O., Melkov, G. A. & Slavin, A. N. Thermalization of a parametrically driven magnon gas leading to Bose-Einstein condensation. Phys. Rev. Lett. 99, 037205 (2007).
Acknowledgements
Work in Münster has been supported by the Deutsche Forschungsgemeinschaft. N.G.B acknowledges EU FP7 ITN project CLERMONT4.
Author information
Authors and Affiliations
Contributions
P.N-B. carried out the measurements, performed preliminary data analysis and contributed to the manuscript writing; O.D. carried out the measurements and contributed to the manuscript writing; V.E.D. developed the experimental technique and wrote the manuscript; N.G.B. developed theoretical model and wrote the manuscript; S.O.D. formulated original idea of the experiment, wrote the manuscript and managed the project.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Nowik-Boltyk, P., Dzyapko, O., Demidov, V. et al. Spatially non-uniform ground state and quantized vortices in a two-component Bose-Einstein condensate of magnons. Sci Rep 2, 482 (2012). https://doi.org/10.1038/srep00482
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00482
This article is cited by
-
Vortices in Andreev–Bashkin Superfluids
Journal of Low Temperature Physics (2024)
-
Classical analog of qubit logic based on a magnon Bose–Einstein condensate
Communications Physics (2022)
-
Advances in coherent magnonics
Nature Reviews Materials (2021)
-
Moiré pattern of interference dislocations in condensate of indirect excitons
Nature Communications (2021)
-
Evidence for spin current driven Bose-Einstein condensation of magnons
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.