Abstract
A new mechanism of particle acceleration, driven by the rotational slow down of the Crab pulsar, is explored. The rotation, through the time dependent centrifugal force, can efficiently excite unstable Langmuir waves in the electron-positron (hereafter e±) plasma of the star magnetosphere. These waves, then, Landau damp on electrons accelerating them in the process. The net transfer of energy is optimal when the wave growth and the Landau damping times are comparable and are both very short compared to the star rotation time. We show, by detailed calculations, that these are precisely the conditions for the parameters of the Crab pulsar. This highly efficient route for energy transfer allows the electrons in the primary beam to be catapulted to multiple TeV (~ 100 TeV) and even PeV energy domain. It is expected that the proposed mechanism may, unravel the puzzle of the origin of ultra high energy cosmic ray electrons.
Similar content being viewed by others
Introduction
Conversion of even a small fraction of the enormous energy released in the rotational slowdown of pulsars (spinning neutron stars) into particle kinetic energy could create ultra high energy cosmic ray electrons. Most significant observational results in the realm of high energy cosmic ray electrons, beginning to be explored by the H.E.S.S., Pamela and Fermi collaborations1,2,3,4, may be summarized as: 1) the 2008 announcement of the H.E.S.S. collaboration showing evidence for a substantial steepening in the energy spectrum of cosmic ray electrons above 600 GeV1, 2) Detection of cosmic-ray electrons up to 1 TeV and confirmation of an excess of VHE leptons in cosmic-rays2,3 by the new instruments on board the Fermi spacecraft have. A thorough analysis of the observational data (of the Fermi telescope) on millisecond pulsars (the surface magnetic field close to Bst ~ 108.5 G) by Kisaka & Kawanaka points to the existence of extremely high energy (≥ 50 TeV) electrons5.
The pulsar rotation and the dark matter annihilation have been suggested as two possible energy sources that could accelerate electrons to such ultra-relativistic regimes4. All known pulsars are observed with decreasing spinning rates. The Crab pulsar, rotating with a period P ≈ 0.0332 s, has a characteristic slow down rate  . The corresponding slowdown luminosity,
. The corresponding slowdown luminosity,  , is determined by the moment of inertia
, is determined by the moment of inertia  , the star radius Rst ≈ 106 cm, the angular velocity Ω ≡ 2π/P and the pulsar mass
, the star radius Rst ≈ 106 cm, the angular velocity Ω ≡ 2π/P and the pulsar mass  where
where  is the solar mass. Out of this prodigious output
is the solar mass. Out of this prodigious output  , only a part ~ 2 × 1038 erg/s is sufficient to power the Crab Nebula; the rest - almost 60% of the released energy is, thus, available and seeks new channels of exploitation.
, only a part ~ 2 × 1038 erg/s is sufficient to power the Crab Nebula; the rest - almost 60% of the released energy is, thus, available and seeks new channels of exploitation.
The substrate for affecting the desired energy transformation is provided by the star magnetosphere. In the standard model for the pulsar magnetosphere6,7, an electrostatic field uproots electrons from the pulsar's surface and accelerates them to relativistic energies along the curved magnetic field. The relativistic electrons emit copious curvature radiation. The emitted photons that have energies beyond the pair production threshold 2 mc2 (m = electron mass ,and c = speed of light), in turn, create electron-positron pairs via γ + B → e+ + e− + γ′ (B is the dipolar magnetic field). Newly produced pairs are further accelerated and emit photons; The cascade lasts till the nascent pair plasma, especially in regions farthest from the star, is dense enough to screen out the initial electrostatic field8,9.
The height h of the gap region (where the electric field is nonzero) is, therefore, strictly limited imposing an upper limit on the maximum attainable electron energy. The potential difference in the gap has been estimated to be  10, where B12 ≡ B/1012 G ≈ 6.7 is the dimensionless magnetic induction. Thus in the potential difference predicted by the standard gap model, the electrons may reach Lorentz factors of ~ 4 × 106 - not sufficient to explain the observed very high energy (VHE) radiation. Figure 1 shows the schematic representation of the distribution function of plasma particles in standard models of the pulsar magnetosphere. The primary beam particles are shown by the narrow shaped area with the Lorentz factor γb. The wider region represents the distribution of secondary electron-positron pairs, characterized by a corresponding Lorentz factor, γp when the distribution function has a maximum value.
10, where B12 ≡ B/1012 G ≈ 6.7 is the dimensionless magnetic induction. Thus in the potential difference predicted by the standard gap model, the electrons may reach Lorentz factors of ~ 4 × 106 - not sufficient to explain the observed very high energy (VHE) radiation. Figure 1 shows the schematic representation of the distribution function of plasma particles in standard models of the pulsar magnetosphere. The primary beam particles are shown by the narrow shaped area with the Lorentz factor γb. The wider region represents the distribution of secondary electron-positron pairs, characterized by a corresponding Lorentz factor, γp when the distribution function has a maximum value.
The distribution function versus the Lorentz factor.
As is clear from the plot, the function consists of two parts: the first - wider region concerns the plasma component corresponding to the cascade processes of pair creation and the second one characterizes the primary Goldreich-Julian beam electrons.
Results
In this paper, we have constructed a theoretical framework for a very efficient and powerful mechanism for generating ultra high energy cosmic ray electrons. A highly relativistic electron-positron plasma in the magnetosphere of a pulsar, converts, the pulsar rotational slow down energy into Langmuir waves at rates that are several orders of magnitude faster than the star rotation period. These waves, in turn, via the well known and understood process of Landau damping, rapidly and preferentially, transfer the electric field energy to very high energy primary electron beam, accelerating them to even higher energies. It is shown that the radiation losses of various kinds do not much affect the very fast energy transfer process. Since the pulsar slowdown energy budget is enormous, charged particles could draw almost unlimited amount of energy via this mechanism. This rather general mechanism, that could encompass, for instance, the magnetospheres of active galactic nuclei (AGN) and accelerate charged leptons as well as hadrons, could crucially advance the understanding of cosmic ray energetics.
Discussion
The determining parameters of the system are: the ratio of the mode frequency to the star rotation frequency w = ω1/Ω and  and b. From our extensive numerical studies, we pick up two typical Mathematica plots (Fig. 2 and Fig. 3) in which ReN1, ImNI, ReN2 and ImN2 are plotted as functions of time. Time has been normalized to the inverse of the frequency ω1, the relativistic plasma frequency corresponding to the stream with lower γ (and much higher ambient density). The parameters for the illustrative cases are: For Fig. 2, w = b = 107, α = .01 and for Fig. 3, w = b = 108, α = .01. Since the x axis denotes time measured in their respective plasma time (inverse of ω1) - the “absolute” time scales in the two figures are different by a factor
and b. From our extensive numerical studies, we pick up two typical Mathematica plots (Fig. 2 and Fig. 3) in which ReN1, ImNI, ReN2 and ImN2 are plotted as functions of time. Time has been normalized to the inverse of the frequency ω1, the relativistic plasma frequency corresponding to the stream with lower γ (and much higher ambient density). The parameters for the illustrative cases are: For Fig. 2, w = b = 107, α = .01 and for Fig. 3, w = b = 108, α = .01. Since the x axis denotes time measured in their respective plasma time (inverse of ω1) - the “absolute” time scales in the two figures are different by a factor  . For each case, we choose initial conditions (t = 0) for what we call the Sin solution: N1(0) = 0, N1′(0) = 1, N2(0) = 0, N2′(0) = α(cos b – i sin b); it is easy to verify that these constitute a consistent solution to the coupled differential equations in the limit t → 0.
. For each case, we choose initial conditions (t = 0) for what we call the Sin solution: N1(0) = 0, N1′(0) = 1, N2(0) = 0, N2′(0) = α(cos b – i sin b); it is easy to verify that these constitute a consistent solution to the coupled differential equations in the limit t → 0.
Here are the principal relevant results of our numerical investigations:
-
a
After an initial gestation time t/w ≪ 1 (not displayed in the figures), the instability builds up with substantial growth rates as b approaches w; the latter is the regime in which the two streams interact, the interaction being the cause of instability.
-
b
Since the two streams are assumed to have different intrinsic plasma frequencies (
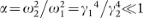 ) the time dependence of (ReN1, ImN1) and (ReN2, ImN2) are quite different. It can be seen from the figures that although (ReN1, ImN1) oscillate (at a new slow frequency, the plasma oscillations are very fast and ever present but are not resolved in the pictures) and grow, the amplitudes (ReN2, ImN2) simply grow. The growth is exponential as predicted by the Floquet theory of differential equations with periodic coefficients. For the solution in Fig. 2, the growth time Γ−1 ≈ 2000 plasma times ≈ 2 × 10−4 P, while the growth time for the solution in Fig. 3 is Γ−1 ≈ 6000 plasma times ≈ 6 × 10−5 P. The growth rates (times) are very high (small) compared to the frequency (period) of star rotation.
) the time dependence of (ReN1, ImN1) and (ReN2, ImN2) are quite different. It can be seen from the figures that although (ReN1, ImN1) oscillate (at a new slow frequency, the plasma oscillations are very fast and ever present but are not resolved in the pictures) and grow, the amplitudes (ReN2, ImN2) simply grow. The growth is exponential as predicted by the Floquet theory of differential equations with periodic coefficients. For the solution in Fig. 2, the growth time Γ−1 ≈ 2000 plasma times ≈ 2 × 10−4 P, while the growth time for the solution in Fig. 3 is Γ−1 ≈ 6000 plasma times ≈ 6 × 10−5 P. The growth rates (times) are very high (small) compared to the frequency (period) of star rotation. -
c
For a moderate and not too small α, the primary determinant of the instability gestation time and growth rate is the relative value of b = 2 ck/Ω sin φ− and w = ω1/Ω. Out of these, ω1 and Ω are determined by the pulsar phenomenology. To bring b to the range of strong instability, one has to choose k sin φ− to be in the desirable range. In principle, then, for any finite sin φ−, one can find a range of k for strong growth. The centrifugal drive for Langmuir waves is, therefore, very robust and effective over a wide spectrum.
The next major step, after establishing that the star rotation energy can be rapidly converted into charge separation electrostatic fields, is to show how this field energy can be harnessed, via Landau damping, to boost highly energetic particles to super high energies. We remind the reader that, although, the Langmuir waves are produced and sustained by the bulk e± plasma characterized by the relatively lower γ region of the distribution (Fig. 1), we want them to damp on the primary beam electrons that have Lorentz factors as high as γb ~ 107 (small blip on the high γ of Fig. 1)11.
Electrostatic waves in relativistic e± plasmas12,13 allow a very simple solution when the wave phase speed is very close to the speed of light, υph ≡ ωr/k ≈ c. In this limit, of utmost relevance to the energy transfer mechanism, the real part of the dispersion relation reads12

where β = 〈γ〉/〈2γ3〉 is a very small parameter 〈〉 denotes momentum averaging and k0 is the limiting value of k for which the phase speed is exactly c. The condition k ≥ k0, implying υph ≤ c defines the regime in which such a wave could strongly interact with physical particles.
Since the Langmuir waves with k approaching k0, have phase velocities asymptotically close to c, they will preferentially damp on and energize the primary electron beam particles endowed with the highest γ. For optimal transfer of centrifugal energy to particle acceleration, the rate of generation of Langmuir waves (measured by Γ, the instability growth rate) and the Landau damping rate13

should be comparable. In Eq.(2), n, γ and  denote respectively the number density, the Lorentz factor and the plasma frequency of the primary beam.
denote respectively the number density, the Lorentz factor and the plasma frequency of the primary beam.
A set of representative two-stream unstable e± plasma parameters that yield Γ ~ ΓLD, is given by γ2 = 4700 and if γ1 ≈ 800. The corresponding instability time = damping time of 10−4 s is several orders of magnitude less than the pulsar rotation period; the rate of energy transfer to the waves and then on to the particles is extremely fast. It is worth noting, that despite the extremely efficient energy transfer to particles, the strength of the pumping process is maintained because the Langmuir waves are continuously generated drawing energy from the star slow down; the latter is taken to be an ”inexhaustible” source. The non-linear effects (caused by the interaction between waves and particles) should be investigated at some stage, but we do not expect substantial difference in the results due to the ”constancy” of the generation process.
Since it is the electron-positron plasma that supports and feeds the two-stream instability, the corresponding characteristic energy in the unstable waves is of the order of the energy accumulated (transferred from star rotation) in the plasma components. Remembering that the number density associated with the e±-plasma far exceeds that of the beam component, the energy gained per beam electron could be extremely large if a substantial fraction of total “available” energy in plasma components were transferred via the electrostatic fields. Dispensing with technical details, we state here that, at the end of the process, a beam electron could end up gaining energy as high as,

where F ≈ 2 mcΩξ(r)−3 14 is the centrifugal force. For typical magnetospheric parameters (the stream density n1 ≈ 2.5 × 1011 cm−3, the primary beam density nb = nGJ ≈ 2 × 107 cm−3), the energy acquired by a beam electron could get to be very high - in 100 s of TeVs, even PeVs.
Highly relativistic particles will, inevitably, loose energy via radiation. We have, therefore, investigated how radiation will affect the overall energy transfer process worked out in this paper. We find that neither the inverse Compton cooling (in Klein-Nishina regime)15,16, nor the synchrotron mechanisms impose significant constraints on the maximum available energy. Very high energy electrons, with particle energy density exceeding the magnetic energy density by many orders of magnitude, move, practically, in a straight line. For them, the curvature radiation is also not expected to interfere with our fast energy transfer mechanism. Equally important is the fact that the ultra-relativistic electrons will have extremely small interaction cross sections with pulsar wind particles and interstellar protons so that they can breeze through, almost unimpeded, through the supernova remnants.
Methods
In this section we present our model for studying the energy pumping process from the rotator - pulsar. Here is a two-step theoretical pathway that can, via well-understood plasma mechanisms17,18,19, convert the pulsar slowdown energy to create super relativistic cosmic ray electrons. Taking the Crab pulsar (Bst ~ 7 × 1012 G) to be a representative, we show that:
-
1
The time dependent centrifugal force (exerted by the star rotation) can, parametrically, drive electrostatic plasma (Langmuir) waves in the relativistic e± plasma residing in the star magnetosphere. The Langmuir waves grow through a variant of the two-stream instability with growth rates several orders of magnitude faster than the star-rotation frequency. Unlike the so called oblique modes discussed in20, we focus on the electrostatic waves, because due to extremely strong magnetic fields in the pulsar magnetosphere the particle distribution is one dimensional.
-
2
The electric fields carried by these efficiently excited Langmuir waves can, then, damp, equally efficiently (via Landau damping) on extremely energetic primary beam electrons to accelerate them to ultra-high energies.
The bulk e± plasma (relativistic) that sustains and amplifies the electrostatic waves and the even more relativistic primary electron beam on which the waves damp, are both constituents of the same pulsar magnetospheric region.
To develop an appropriate theory for the centrifugally induced parametric Langmuir instability, we assume the magnetic field lines in the magnetosphere to be almost rectilinear - a good approximation for distances less than the curvature radius of the field lines. In the rotating frame of straight field lines co-rotating with the pulsar, the metric is given by

In the single particle equation of motion (in the 1 + 1 formalism21)

i = e , p is the species index, ei is the charge of the corresponding particle, dτ ≡ ξdt, ξ ≡ (1 − Ω2r2/c2)1/2 is the so-called time lapse function,  is the gravitational potential,
is the gravitational potential,  is the Lorentz factor and pi and Vi are, respectively, the dimensionless momentum (pi → pi/m) and velocity. The first term on the righthand side of the equation represents the centrifugal force and plays a crucial role in our model.
is the Lorentz factor and pi and Vi are, respectively, the dimensionless momentum (pi → pi/m) and velocity. The first term on the righthand side of the equation represents the centrifugal force and plays a crucial role in our model.
In the laboratory frame, Eq.(5) takes the appearance of a fluid equation (see method)

that, in conjunction with the continuity

and the Poisson equation,

defines the entire dynamical system.
If the electromagnetic terms do not contribute to the equilibrium (throughout this paper equilibrium simply means the absence of electromagnetic fields) because of the frozen-in condition E0 + v0i × B0 = 0, Eq. (6) reduces to22

from which we can calculate the particle trajectories. For highly relativistic particles (γ ≫ 1), the equilibrium equation of motion, controlled by the centrifugal force exerted by the star rotation, yields the simple periodic solution,


where V0 ≈ c is the velocity amplitude. The phase φ, necessary to insure a general solution of Eq. (9), was taken to be zero in previous work18. We will soon show that, due to this omission, a crucial ingredient of the current modela strongly growing variant of the ”two stream instability” - was missed in the earlier work.
In our model we are trying to describe an essentially kinetic plasma by a fluid approach. The particle distribution has a wide γ (energy) spectrum (Fig. 1) and time dependent particle velocities have a characteristic phase φ (11). A proper detailed description is likely to be rather involved. In order to extract the main results in a highly reduced description, we will assume that the plasma is multi-stream; each stream has a characteristic γ and a phase φ. By solving the linear, connected dynamics of two such streams, we will demonstrate the emergence of a very interesting manifestation of the two stream instability; the instability will be determined by the phase difference between the streams. Each stream constitutes an electron-positron plasma and Equation (6) is to be viewed as the equation of motion of the specie i (electron or positron) belonging to a given stream.
The orbits (10,11) (calculated using the frozen-in condition), are time dependent and periodic with the periodicity determined by P = 2π/Ω, the star rotation time. Strictly speaking, these are field-free but not equilibrium orbits; they may be considered equilibrium orbits only as long as the characteristic wave time-scales associated with the wave motion (both oscillation and growth) are much shorter compared to P. Because of time dependence of the orbits, the linear wave equations will not be amenable to the standard time - Fourier analysis; the solution of the stability problem will be more involved and nuanced. The periodicity of the equilibrium orbits is what leads to the parametric pumping of particle energy into the energy in the electric field.
Following the ”standard” procedure of splitting the physical variables Ψ = (n, v, p, E,) into equilibrium and perturbed parts, Ψ ≈ Ψ0 + ψ1, expanding the linear perturbations as ψ1(t, r) ∝ ψ1(t) exp [i(kr)], we derive, after some tedious but straightforward manipulations, the two coupled, non-autonomous differential equations


in terms of the perturbed ‘densities' of each stream

The streams 1 and 2 are distinguished through their characteristic γ and the phase φ (for simplicity, we have put the velocity amplitude V0 = c). The frequencies  are, respectively the effective relativistic plasma frequencies (for longitudinal modes) corresponding to the two streams and
are, respectively the effective relativistic plasma frequencies (for longitudinal modes) corresponding to the two streams and

with 2φ± = φ1 ± φ2 and

In deriving Eqs.(12–13), we have invoked (ck/Ω) ≫ 1; this parameter will turn out to be approximately the ratio of the Langmuir frequency to the star rotation frequency and, will lie in the range 106 – 1010.
From the general structure of evolution Eqs.(12 – 13), with definitions (15 – 16), one may draw the following inferences:
-
1
The evolution of the two streams is coupled and the time dependence of the coefficients is fully contained in χ.
-
2
Though χ depends on both the sum and difference of the phases associated with the two streams, the dependence on the phase sum 2φ+ = φ1 + φ2 is trivial and can be absorbed in a redefinition of the time variable; φ+ will be dropped from now on.
-
3
The phase difference φ−, however, emerges as a fundamental parameter of the two-stream system. If φ− = 0, then χ = 0 and the coefficients of Eqs.(12–13) become constants (the system becomes autonomous) leading to the simple dispersion relation ω2 = ω12 + ω22, i.e, the two streams oscillate together with a frequency that is the sum of their individual plasma frequencies. Most importantly, for φ = 0, there is no parametric instability. Strictly speaking, this is only an approximation, since in Eq. (15) we have assumed V0β = c, whereas
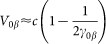 , leading to a nonzero growth rate (even if φ− = 0) which will be less than for nonvanishing values of φ− by many orders of magnitude.
, leading to a nonzero growth rate (even if φ− = 0) which will be less than for nonvanishing values of φ− by many orders of magnitude. -
4
It is only when φ− is non-zero (the two streams remain “distinct”) that the system “notices” the periodic time dependence of the centrifugally driven orbits. Since the time dependence and periodicity of the orbits is, precisely, what drives the strong Langmuir-wave instability, assigning different phases to the particle orbits (10–11) is the key step that allows energy transfer (via instability) from rotational slowdown to the Electrostatic fields carried by the Langmuir waves.
Differential equations with periodic coefficients (like (12–13)), Mathieu equation being the simplest example, are known to display parametric instabilities in well defined regimes. We find this behavior when (12–13) are solved, using analytical (asymptotic) as well as numerical techniques, to determine the time evolution of the densities N1 , N2 (and the electric field,  ). Although the analytic solution is quite instructive, we will dwell here, mostly, on the more general numerical solution. Mathematica solutions demonstrate that model Eqs.(12–13), indeed, harbor parametrically unstable solutions. The charge separation densities (the electric field) grow in time and acquire a hefty growth rate when b ≈ ω/Ω; this qualitative feature is also predicted by the analytical dispersion relation.
). Although the analytic solution is quite instructive, we will dwell here, mostly, on the more general numerical solution. Mathematica solutions demonstrate that model Eqs.(12–13), indeed, harbor parametrically unstable solutions. The charge separation densities (the electric field) grow in time and acquire a hefty growth rate when b ≈ ω/Ω; this qualitative feature is also predicted by the analytical dispersion relation.
References
Aharonian, F. et al. Energy Spectrum of Cosmic-Ray Electrons at TeV Energies. Phys. Rev. L. 101, 261104 (2008).
Abdo, A. A. et al. Fermi Large Area Telescope Measurements of the Diffuse Gamma-Ray Emission at Intermediate Galactic Latitudes. Phys. Rev. L. 102, 181101 (2009).
Ackermann, M. et al. Fermi LAT observations of cosmic-ray electrons from 7 GeV to 1 TeV. Phys. Rev. D. 82, 092004 (2010).
Chang, J. et al. An excess of cosmic ray electrons at energies of 300–800 GeV. Nature 456, 362 (2008).
Kisaka, S. & Kawanaka, N. An excess of cosmic ray electrons at energies of 300–800 GeV. MNRAS 421, 3543 (2012).
Deutsh, A. The electromagnetic field of an idealized star in rigid rotation in vacuo. Ann. Astrophys. 18, 1 (1955).
Goldreich, P. & Julian, W. H. Pulsar Electrodynamics. ApJ,157, 869 (1969).
Sturrock, P. A Model of Pulsars. ApJ 164, 529 (1971).
Tademaru, E. On the Energy Spectrum of Relativistic Electrons in the Crab Nebula. ApJ 183, 625 (1973).
Ruderman, M. A. & Sutherland, P. G. Theory of pulsars - Polar caps, sparks and coherent microwave radiation. ApJ 196, 51 (1975).
Osmanov, Z. & Rieger, F. On particle acceleration and very high energy gamma-ray emission in Crab-like pulsars. A&A. 502, 15 (2008).
Lominadze, D. G., Mikhailovskii, A. B. & Sagdeev, R. Z. Langmuir turbulence of a relativistic plasma in a strong magnetic field. JETP 50, 927 (1979).
Volokitin, A. S., Krasnoselskikh, V. V. & Machabeli, G. Z. Waves in the relativistic electron-positron plasma of a pulsar. Soviet Journal of Plasma Physics 11, 531 (1985).
Rogava, A., Dalakishvili, G. & Osmanov, Z. Centrifugally Driven Relativistic Dynamics on Curved Trajectories. GReGr 35, 1133 (2003).
Rybicki, G. B. & Lightman, A. P. Radiative Processes in Astrophysics. Wiley, New York (1979).
Blumenthal, G. R. & Gould, R. J. Bremsstrahlung, Synchrotron Radiation and Compton Scattering of High-Energy Electrons Traversing Dilute Gases. Rev. Mod. Phys. 42, 237 (1970).
Machabeli, G. Z. Parametric excitation of high-frequency electrostatic waves in a homogeneous cold plasma. SvJPP, 4, 914 (1978).
Machabeli, G., Osmanov, Z. & Mahajan, S. Parametric mechanism of the rotation energy pumping by a relativistic plasma. Phys. Plasmas 12, 062901 (2005).
Machabeli, G. Z. & Tsikarishvili, E. G., Relativistic effects in the parametric excitation of low-frequency electrostatic waves. SvJPP 4, 920 (1978).
Bret, A., Gremillet, L. & Dieckmann, M. E., Multidimensional electron beam-plasma instabilities in the relativistic regime. PhPl, 17, 120501 (2010).
Thorne, K., Price, R. & MacDonald, D. A. Black Holes: The Membrane Paradigm, Yale University Press, New Haven (1986).
Machabeli, G. Z. & Rogava, A. D. Centrifugal force: A gedanken experiment. Phys. Rev. A. 50, 98 (1994).
Author information
Authors and Affiliations
Contributions
M.S., M.G., Z.O. and N.C. developed analytical model. M.S. and O.Z. performed the numerical investigation of the problem, who also wrote the manuscript with the assistance of all other co-authors.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Mahajan, S., Machabeli, G., Osmanov, Z. et al. Ultra High Energy Electrons Powered by Pulsar Rotation. Sci Rep 3, 1262 (2013). https://doi.org/10.1038/srep01262
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep01262
This article is cited by
-
Millisecond newly born pulsars as efficient accelerators of electrons
Scientific Reports (2015)
-
Nonlinear oscillatory and monotonic shocks in dense plasmas with ultra-relativistic degenerate electrons
Astrophysics and Space Science (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.





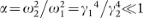 ) the time dependence of (ReN1, ImN1) and (ReN2, ImN2) are quite different. It can be seen from the figures that although (ReN1, ImN1) oscillate (at a new slow frequency, the plasma oscillations are very fast and ever present but are not resolved in the pictures) and grow, the amplitudes (ReN2, ImN2) simply grow. The growth is exponential as predicted by the Floquet theory of differential equations with periodic coefficients. For the solution in
) the time dependence of (ReN1, ImN1) and (ReN2, ImN2) are quite different. It can be seen from the figures that although (ReN1, ImN1) oscillate (at a new slow frequency, the plasma oscillations are very fast and ever present but are not resolved in the pictures) and grow, the amplitudes (ReN2, ImN2) simply grow. The growth is exponential as predicted by the Floquet theory of differential equations with periodic coefficients. For the solution in 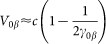 , leading to a nonzero growth rate (even if φ− = 0) which will be less than for nonvanishing values of φ− by many orders of magnitude.
, leading to a nonzero growth rate (even if φ− = 0) which will be less than for nonvanishing values of φ− by many orders of magnitude.