Game Theory, Evolutionary Stable Strategies and the Evolution of Biological Interactions

Evolutionary ecologists aim to understand the complex behavioral relationships between organisms as they interact to obtain resources. In general, these interactions range from antagonistic to cooperative, but cases of exploitation and altruism also occur. Interactions are costly: energy is invested by each organism in both confrontation and cooperation as a means to acquire the resource. Indeed, even avoidance can be costly if energy is expended and no resources are obtained. The energy spent is a cost to the organism, and the resources are benefits. Comparing the relative cost to the benefits obtained following an interaction determines the net gain or loss incurred by the organism, and this value is referred to as the payoff. Different interaction strategies, such as combative or cooperative, result in different payoffs based on nature of the interaction. Evolutionary ecologists treat these strategies as phenotypes. The most successful organisms maximize their payoff and increase their ability to reproduce. In short, the organism with the best interaction strategy has the highest fitness. Since the interaction strategy (phenotype) can directly relate to fitness, the optimum strategy will be favored under natural selection.

Interactions between organisms with either competing or identical strategies can be treated as games with multiple players. Since biological interactions involve two or more decision makers (i.e., individuals with strategies), biologists utilize game theory to elucidate evolutionary consequences of interactions¹. Game theory is a branch of mathematics that investigates the outcomes of multi-individual interactions, in which the payoff for any one individual depends not only on its own strategy, but the strategies of the other individuals involved. An individual does not control the decisions of others. While much of game theory is based on the interactions of rational decision makers (humans), in evolutionary game theory the payoff is a surrogate for fitness and strategies evolve over many repeated iterations of the game^2,3. Estimating fitness for strategies based on the payoff matrix reveals stable payoff equilibriums may be achieved through natural selection, an important feature of evolutionary game theory. Furthermore, stable payoff equilibriums have been shown for cooperation and altruism, behaviors that seem contradictory to the strongly supported individualistic, survival of the fittest mode of evolution³.

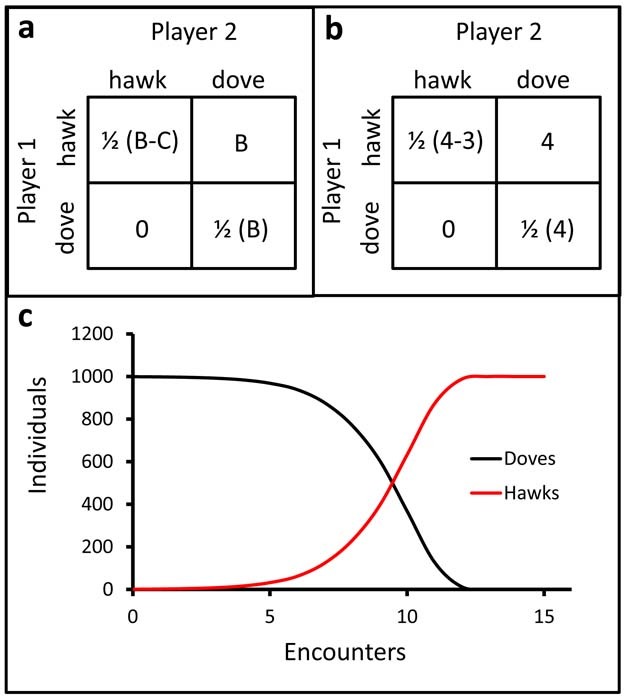
Evolutionary games are often visually represented as a payoff matrix (Fig. 1a), in which the payoff for the individual involved is shown for all possible interactions. In the matrix, the payoffs typically are those assigned to the player depicted in the row playing against the strategy in the column; thus, in Figure 1a, if player 1 is a hawk, and encounters a hawk, the payoff for player 1 is ½ (B-C), the value in the upper left quadrant. If player 1 is a hawk and encounters a dove, the payoff for player 1 is B, the value in the upper right quadrant. The payoffs for player 1 adopting the dove strategy against a hawk and against a dove are in the lower left and lower right quadrants, respectively.

In some populations, all individuals may have the same strategy phenotype. Such a strategy is said to be an evolutionary stable strategy (or ESS) if that strategy cannot be replaced, or invaded by any other strategy through natural selection^4,5. Formally, and ESS must satisfy two conditions⁴: 1) an individual employing strategy A must do better against another individual employing strategy A than any other strategy; and 2) should a new strategy evolve (A') that does equally well against strategy A, for A to be an ESS, an individual employing strategy A must do better against an individual employing strategy A' than an individual employing strategy A'.To illustrate an ESS, let us consider a payoff matrix between two organisms each with an aggressive strategy and a passive strategy: the classic ‘hawk vs. dove' game⁴ (Fig. 1a)⁴. A hawk is aggressive and initiates a combative interaction when confronted; alternatively, the dove is passive and avoids combative interactions. A hawk may encounter another hawk, or a dove; likewise, a dove may encounter another dove, or a hawk. If the two individuals adopt a dove strategy, the resources are partitioned equally. If a dove encounters a hawk, the hawk acquires the totality of the resource, while the dove receives none. Lastly, if a hawk encounters another hawk, the resources are partitioned equally; however, there is a cost incurred by each hawk due to the aggressive interaction. A population of doves may be invaded by a hawk, and the hawk strategy will displace the dove strategy (Fig. 1c). However, the hawk strategy is an ESS only if the value of the resource is greater than the cost of the conflict (B > C > 0). If the cost of conflict is greater than the reward, then neither the hawk nor the dove strategy satisfies the conditions of ESS as a pure strategy.

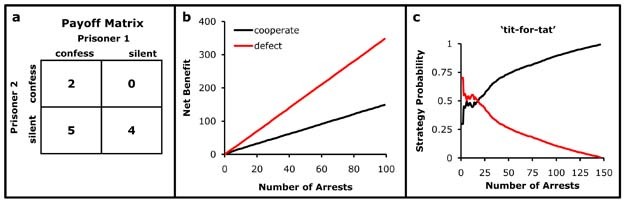
The hawk vs. dove game reveals that competitive strategies may reach a stable evolutionary equilibrium, but how can a cooperative strategy persist in an evolutionary equilibrium? Consider another classic game theory problem - the Prisoners' Dilemma. The conditions of the Prisoners' Dilemma are such that two prisoners are captured for, and guilty of the same crime, and each prisoner has the choice to confess or to remain silent. Examining the payoff matrix (Fig. 2a), the largest mutual benefit occurs when both prisoners remain silent. However, the highest possible benefit for a single prisoner occurs when he confesses, and implicates the other, while the second prisoner remains silent. If both confess, there is a reduced punishment for both. For instance, if prisoner 1 confesses and prisoner 2 remains silent, prisoner 1 is rewarded and prisoner 2 receives the harshest punishment. If prisoner 1 always chooses to confess, he avoids the harshest punishment. If we consider only a single encounter between prisoners, then the only evolutionary stable strategy is to always confess and implicate the other prisoner (Fig. 2b).

How does this example lead to cooperation in biological interactions? For biological interactions, it is generally assumed that the same two individuals will interact more than once (so called iterated prisoners' dilemma)³. At the population level, the game will be repeated over evolutionary time scales (hundreds to thousands of generations or more). Recall that cooperation results in the highest mutual benefit for both players. Thus, with repeated games cooperation can evolve through the simple strategy of ‘tit for tat' described by Axelrod and Hamilton3. In the ‘tit for tat' strategy, individual 1 begins the game with cooperating (remaining silent). In subsequent iterations of the game, individual 1 uses the strategy of individual 2 from the previous round. That is to say, if individual 2 cooperated in the first round, then individual 1 will cooperate in round two. Likewise, individual 1 will confess in round two if individual 2 confessed in the first round. The strategy was tested using computer simulations, and cooperation emerged as an evolutionary stable strategy if the probability of two individuals meeting more than once was sufficiently high³ (Fig. 2c). Thus, cooperation can evolve in small populations through strategies based on simple reciprocity.

The examples so far have used two-player, fixed payoff games to demonstrate the evolution of different interaction strategies. Biological interactions and strategies are often more complex. Strategies are considered pure if the behavior is constant for all interactions, or they may be considered mixed if the behavior expressed is conditional on the organisms involved^4,6. For instance, a mixed strategy may be size related: avoid larger individuals and attack smaller individuals. The value or quality of the benefit also influences strategies. From an evolutionary standpoint, the reward for competitive behavior must outweigh the risk and cost of competition. Thus, low quality resources are unlikely to drive intense combat. However, the higher the quality or importance of the benefit, the more intense the competition will be.

Consider that many animal species are strongly territorial, and territories vary in quality. If a larger individual encounters a smaller individual, the larger individual will often begin aggressive gestures towards the smaller individual. The smaller individual will often flee to avoid the conflict. The likelihood of the larger individual being hurt or killed by the smaller individual is minimal, so the risk of the aggressive behavior is minimal. Likewise, the smaller individual must avoid conflict with larger individuals in which they may be severely harmed or killed. Smaller individuals often establish lower quality territories, but still have the opportunity to reproduce. The most intense conflicts occur between individuals of equal size fighting for higher quality territories, and in this fighting both individuals may receive sufficient damage due to combat so that neither can reproduce. The benefit of avoiding these detrimental costs of combative encounters has led to the evolution of ritualized combat for mates and territory where the contestants avoid severe harm. Common examples of ritualized combat include male fiddler crabs that engage in displays of the larger claw to demonstrate superiority, black rat snakes that engage in elaborate instigator-responder movements, and male red deer that bellow and display their antlers to potential combatants competing for mates. These visual cues that animals display often avoid combat when an individual demonstrates physical superiority; however, combat may escalate between evenly matched individuals or when the seemingly inferior combatant continues the aggressive display.

In the prior examples, we assume a uniform environment, and resources are available everywhere. In natural environments, spatial and temporal variability in resource abundance and quality influence biotic interactions^7,8; moreover, organisms modify the environment by utilizing resources. Payoff matrices may be either symmetric or asymmetric. In symmetric payoff matrices, payoffs are identical for each individual based on the interaction, whereas payoffs may be different for each individual in an asymmetric payoff matrix. A common asymmetric game occurs between organisms competing for territories in which one player occupies the territory and the other is the intruder. The payoff in the game is the territory, and the asymmetry is that the territory holder may either maintain or lose the territory, while the intruder may or may not acquire the territory. The territory holder is more likely to escalate the conflict via an aggressive strategy to protect the territory, while the intruder is less likely to escalate⁹. A second asymmetry that arises in animal conflicts is the different abilities to acquire or hold a resource such that the cost of escalating the interaction differs due to combative capability¹⁰. Here, the superior competitor is more likely to employ an aggressive strategy.

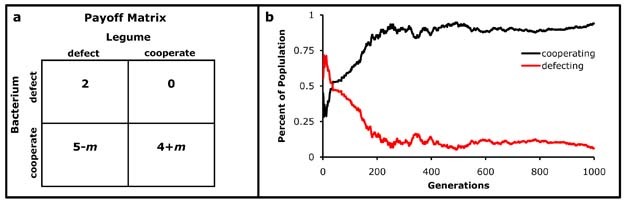
Payoff modification is possible under both symmetric and asymmetric models in which individuals have the ability to reward more beneficial partners and punish non-cooperators¹¹. The ability to modify payoffs based on partner interactions is a fundamental component to most mutualism stability theories¹². Consider a symmetric payoff matrix in which payoffs are modified based on cooperation or cheating (Fig. 3a). Here is a model for two symbiotic organisms involved in trade for resources. For example, consider a legume (bean plant) that associates with bacteria that provide nitrogen the plant can use. These bacteria live within special nodules on the plant root and rely on the plant for energy in the form of sugar. Thus, cooperation involves an investment by both partners. In the payoff matrix, a modification value (m) increases the payoff if both partners cooperate. If cheating occurs (one partner cooperates, the other does not), then the payoff is reduced by m. If a bacterium receives more sugar, it is able to provide more nitrogen to the plant. Given more nitrogen, the plant can photosynthesize more to produce sugars. There is thus a positive feedback for cooperation. So long as the partners trade with fidelity (an increase in benefit is reciprocated honestly), cooperation emerges as an ESS (Fig. 3b).

Evolutionary game theory in which cooperation is rewarded with fidelity provides rationale for altruistic behavioral strategies seemingly incongruent with natural selection. In evolutionary terms, altruism occurs when an individual reduces its own immediate fitness probability (i.e. its likelihood to reproduce in the short term) to improve the fitness of another individual. Altruism is most common in animals that exhibit social behavior, such as warning calls or food sharing, and colony forming behavior. The benefit of warning calls and food sharing is based on reciprocal altruism, namely that the benefits provided to others will be returned in the future¹³. A bird that provides a warning call is temporarily more apparent to predators, thus reducing its immediate fitness probability. However, the same bird may benefit in the future from warning calls from other birds. Likewise, a vampire bat that regurgitates its food to feed hungry bats will benefit from the same service when it is unable to find food¹⁴. Reciprocal altruism relies on organisms interacting multiple times, and game theory provides a framework for the evolution of reciprocal altruism via the prisoners' dilemma described earlier. The iterated prisoners' dilemma typically involves repeated interactions between small numbers of prisoners; however, altruism has been shown to evolve even in large groups through a combination of direct and indirect altruistic reciprocity¹⁵. Direct reciprocity occurs when the same two individuals interact repeatedly, while indirect reciprocity is when subsequent interactions are between different partners. In sum, while altruistic behavior may temporarily reduce the fitness of the individual, reciprocal altruism increases fitness over the lifetime of the individual.

(Note: Inclusive fitness is a common explanation for the evolution of altruistic behavior that does not necessarily depend on game theory. Altruistic alleles increase in a population if the cost to the altruistic individual is less than the reproductive benefit of the recipient multiplied by the likelihood of the recipient passing on the altruistic allele to its offspring (Hamilton's Rule)¹⁶. Inclusive fitness is often associated with kin selection, as more closely related organisms more likely share the same alleles - such alleles are referred to as ‘identical by descent' as they are from a common ancestor. However, altruism genes may be found in non-related individuals, thus relatedness is not a strict requirement of inclusive fitness.)

The principles of game theory provide a theoretical framework for understanding the evolution of biological interactions. Evolutionary game theory applies to organisms that interact repeatedly, both within a generation and over evolutionary relevant timescales. In special cases, evolutionary stable strategies emerge in which a particular strategy is adopted by all members of a population and alternative strategies (mutant phenotypes) cannot invade and displace the ESS. The flexibility of game theory allows for the testing of complex mixed strategies and incorporating reward and punishment in evolutionary strategies. Importantly, game theory demonstrates the evolution of cooperation and altruism ESSs is consistent with evolution through natural selection.