Main

When a Hamiltonian is invariant with respect to a continuous symmetry, but the ground state is not, a massless bosonic mode appears in the spectrum of allowed excitations5. At temperatures low enough for quantum effects to become prominent, dynamical behaviours, such as superconductivity and superfluidity, are possible only due to the low-energy excitation spectrum. Superfluid and superconducting states break gauge invariance and the resultant Goldstone mode is an oscillation of the phase of the order parameter giving rise to a collective motion of particles that is distinct from single-particle excitations. In superconductors, the Coulomb interaction lifts the collective mode up to the frequency of the classical plasma oscillation4, present in the normal phase, such that the Goldstone mode is generally imperceptible6. In neutral superfluids, however, the Goldstone mode takes the form of a gapless phonon7 and provides a dramatic signature of macroscopic order.

Ultracold gases of atomic fermions have enabled the creation and study of high-transition-temperature superfluids in the smooth crossover from the BCS to BEC regimes8. Both first-sound9,10,11 and second-sound10 propagation have been observed in inhomogeneous Fermi gases, yet the basic elementary excitation spectrum has not been measured. Here, we present a comprehensive study of the low-temperature excitations in a homogeneous Fermi superfluid throughout the whole BCS–BEC crossover. The spectra exhibit both a dominant Goldstone mode, or Bogoliubov–Anderson (BA) phonon, and a single-particle continuum. Our study reveals how the energy and spectral weight of these excitations evolve as a function of the interaction strength. We develop a theory based on the quasiparticle random-phase approximation (QRPA), which provides a good quantitative description of the data.

The starting point for our experiments is a harmonically trapped gas of fermionic 6Li atoms in a balanced mixture of the lowest two hyperfine states with tunable s-wave interactions near a broad Feshbach resonance (see Supplementary Information). Atoms are cooled to temperatures below the superfluid transition temperature, Tc, across a wide range of the BCS–BEC crossover12. We measure the density–density response of these gases using two-photon Bragg spectroscopy13,14,15. This is the cold-atom analogue of inelastic neutron scattering, which has enabled characterization of the dispersion relation, roton minimum, and condensate fraction in superfluid helium3; and inelastic X-ray scattering, used to measure electronic excitations in strongly correlated materials16. Using tightly focused Bragg lasers that intersect in the centre of a trapped atom cloud, we scatter atoms from a region of near-homogeneous density (Fig. 1a). Bragg scattering involves the absorption of a photon with energy ℏωa, where ℏ is Planck’s constant, and wavevector ka from one laser beam, and stimulated emission of a photon with energy ℏωb and wavevector kb into a second beam, thereby transferring energy ℏω = ℏ(ωa − ωb) and momentum ℏ k = ℏ(ka − kb). Within linear response the total momentum imparted to the cloud, Px, is proportional to the imaginary part of the dynamic susceptibility or density–density response function, (see Supplementary Information).

Figure 1: Probing homogeneous excitation spectra with focused beam Bragg scattering.
figure 1

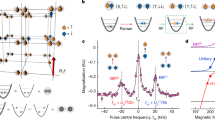
a, Two far-detuned Bragg lasers, focused to 20 μm 1/e2 radii, intersect at an angle of 12.9° in the centre of a harmonically trapped Fermi gas. b,c, Difference between images of atom clouds with and without Bragg scattering of single particles above the pair-breaking continuum at 1/(kFa) = −0.6 in the BCS regime (b), and the BA phonon at unitarity (c). Purple ellipses indicate the size of the expanded clouds and the dashed lines intersect the cloud centre. Each optical density (OD) image is 400 μm by 180 μm. The Bragg laser intensities used in b were 2.4 times higher than those in c due to the weaker response of single particles compared with the collective BA mode. d,e, Calculated excitation spectra for 1/(kFa) = −0.6 (d) and 0.0 (e). The green circles mark the (ω, k) coordinates of the Bragg excitation used in b and c and the red lines indicate the threshold for single-particle excitations (2Δ).

Full size image

Bragg spectra are obtained by applying a 1.2 ms Bragg pulse and measuring Px as a function of the Bragg frequency ω. A Bragg spectrum provides full information on the energy and spectral weight of particle-conserving excitations at momentum ℏ k (ref. 17). After applying the Bragg pulse, atoms are released from the trap and we determine the centre-of-mass displacement, ΔX ∝ Px, of the Bragg scattered volume, with respect to the unperturbed atoms, after 2 ms time of flight15. In the measurements that follow, the mean atomic density in the Bragg volume, , lies in the range , where n0 is the peak density in the trap centre (see Supplementary Information).

Figure 1b shows the difference between two time-of-flight images of atom clouds, with and without Bragg scattering, on the BCS side of the Feshbach resonance for an interaction strength of 1/(kFa) = −0.6 (875 G), where is the Fermi wavevector and a is the s-wave scattering length. Bragg scattering removes atoms from the centre of the cloud, where the lasers overlap, and displaces them along x. Here, ω lies in the single-particle continuum, indicated by the green circle on the excitation spectrum (Fig. 1d), calculated for 1/(kFa) = −0.6 using the QRPA theory (see Supplementary Information). The Bragg frequency is normalized by the Fermi energy, which is set by the mean density EF = kBTF = ℏ2kF2/(2m), where kB is Boltzmann’s constant and m is the atomic mass.

Figure 1c shows a difference image taken with ω tuned to the peak of the BA phonon mode (Fig. 1e) at unitarity 1/(kFa) = 0.0. Comparing Fig. 1b with 1c reveals a qualitative difference between single-particle and phonon (collective) excitations. Phonons are a density modulation (sound wave) with the periodicity of the Bragg lattice, excited when the lattice velocity (ω/k) equals the sound velocity cs. As the phonon propagates along x and the cloud expands, the density continuously decreases and so too does the local speed of sound (gradient of the dispersion). To conserve energy and momentum, the phonon decays into lower-energy modes, whose wavevectors need not be parallel, in a manner reminiscent of Beliaev damping18. While the density-dependent decay dynamics may be quite complex, the qualitative result is a long-wavelength density modulation propagating along x (Fig. 1c). In contrast to the case of single-particle scattering, the density minimum no longer remains fixed at the location of the Bragg lasers.

We have measured a series of Bragg spectra at k ∼ kF/2, within the linear response regime, that map the low-temperature excitations for a range of interaction strengths, plotted in Fig. 2 (see Supplementary Information). For 1/(kFa) = −0.9 and −1.6, (rightmost traces in Fig. 2) we observe only single-particle excitations. Here, the pair correlation length, ξpair (ref. 19), exceeds 1/k and the phonon mode merges with the single-particle continuum for k < kF/2(refs 20,21). Closer to the Feshbach resonance, the Goldstone mode (BA phonon) first appears around 1/(kFa) ≲ −0.5, where ξpair ≈ 1/k (ref. 19), and is identified using a Gaussian fit (shaded blue). At unitarity, the BA mode dominates the spectra and the single-particle branch is increasingly suppressed. In the BEC regime single-particle excitations fall below our measurement sensitivity due to the reduced spin-susceptibility22 as fermion pairs become more tightly bound.

Figure 2: Bragg spectra throughout the BCS–BEC crossover.
figure 2

Blue and red points are experimental data, solid blue lines are Gaussian fits to the BA mode peak (shaded blue) and the red shaded region indicates the single-particle excitation branch. The Bragg laser intensities are varied as the interactions are tuned from the BCS to BEC regime to maximize the signal-to-noise while remaining in the linear response regime (see Supplementary Information). plotted above has been scaled by the ratio of the relative two-photon transition probabilities so that all spectra can be displayed on the same scale. Error bars represent the standard deviation of the measured centre-of-mass displacements.

Full size image

The local temperature within the Bragg volume is T/TF = 0.09(1) at unitarity (just over 0.5Tc), determined by fitting the density profile to the known equation of state23. While direct thermometry away from unitarity remains a challenge, tuning to the BCS (BEC) regime by scanning the magnetic field adiabatically around the Feshbach resonance will decrease (increase) T/TF such that we expect T to remain below Tc for all spectra. Our calculated temperatures following an adiabatic sweep to the limiting interaction strengths of 1/(kFa) = −1.6 and +1.1 are T/TF = 0.02(1) and 0.10(2), respectively12. In the BEC regime, 1/(kFa) ∼ +1, we observe condensate fractions exceeding 80%. A recent study of second-sound propagation in a unitary Fermi gas found that the superfluid fraction approaches unity for T ≲ 0.1TF (ref. 10). Hence, our measurements in the strongly interacting regime represent the low-temperature (near ground-state) excitations.

In the range −0.5 ≤ 1/(kFa) ≤ 0, both phonon and single-particle excitations are visible in the individual spectra. Furthermore, for −0.2 ≤ 1/(kFa) ≤ 0, these two branches separate from each other, enabling direct read-off of the superfluid pairing gap Δ. Figure 3a shows a zoomed view of the Bragg spectrum at unitarity. Filled points are experimental data and the shaded curve is the QRPA theory including the Fourier width of the Bragg pulse. Since a minimum energy of ℏω = 2Δ is required to break a pair and produce two free atoms, we associate the sharp onset of single-particle excitations with 2Δ (dotted vertical line). At unitarity we find Δ/EF = 0.47 ± 0.03. The pairing gap has previously been measured using momentum24 and spatially resolved25 radiofrequency spectroscopy. Our localized Bragg measurements are consistent with previous radiofrequency data25, yet provide the pairing gap directly, free of final-state effects, Hartree energy shifts or density inhomogeneities. Figure 3b, c shows spectra for 1/(kFa) = −0.11 and 1/(kFa) = −0.21, respectively. A plot of Δ/EF for these three spectra is provided in Fig. 3d along with different calculations12,26,27,28,29,30.

Figure 3: Bragg spectra and pairing gap near unitarity.
figure 3

a, Experimental spectrum at unitarity (filled data points) and QRPA theory (shaded). Vertical dotted lines indicate the onset of the single-particle branch for ℏω ≥ 2Δ (EF = 12.1 kHz). Inset: comparison of experimental and theoretical BA mode peaks. b,c, Zoomed view of Bragg spectra at 1/(kFa) = −0.11 and 1/(kFa) = −0.21. d, Pairing gap Δ determined from Bragg spectra (blue points) along with previous radiofrequency (RF) measurements (green triangles)25 and theoretical predictions: BCS (black dotted line), T-matrix (green dashed)26, Luttinger–Ward (black solid)12, Gaussian fluctuation theory (red dash-dotted)28, Monte Carlo (brown cross)27, operator product expansion (red asterisk)29, and extended T-matrix (purple dash-dot-dotted)30. Error bars in a–c denote the standard deviation of the measured centre-of-mass displacements. Error bars in d are calculated by combining the uncertainty in determining with the finite spectral resolution of the measurements.

Full size image

The experimentally determined pairing gap can serve as an input parameter for our diagrammatic theory, which uses the chemical potential as a fitting parameter (see Supplementary Information). We find good agreement between our QRPA calculation and experiment over the full excitation spectrum (shaded curves, Fig. 3), particularly in the frequency of the BA mode. When the theory is scaled to match the amplitude of the experimentally measured single-particle branch, the calculated BA mode is consistently more than twice as high and approximately two-thirds the width of the measured peak (inset, Fig. 3a). Damping mechanisms31, not included in the theory, may explain this discrepancy.

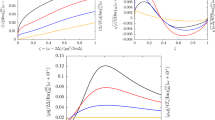
As k → 0, the BA mode displays linear dispersion with a gradient set by the sound velocity cs. The centre frequency of the BA mode ωBA is found from a Gaussian fit to the BA peak (solid blue lines, Fig. 2) providing a measure of cs/vF = ωBA/(kvF), where vF = ℏkF/m is the Fermi velocity. This is plotted in Fig. 4 (blue circles) for interactions where we obtain a reliable fit. In the momentum range used here, 0.4 ≲ k/kF ≲ 0.6 (see Supplementary Information), the dispersion remains close to linear near unitarity, but becomes concave (convex) in the BCS (BEC) regime21,26,31. We can estimate this curvature for finite k/kF using the QRPA calculation and correct for it to estimate cs/vF as k → 0 (see Supplementary Information). The corrected data (orange diamonds in Fig. 4) agree well with theoretical calculations of cs/vF throughout the BCS–BEC crossover12,28,30,32 and also with previous experiments9,10,11. Our measurements are the first to probe sound propagation in a homogeneous Fermi gas, allowing direct comparison with theory, free of complications arising from density inhomogeneities and partial hydrodynamics across the wavefront.

Figure 4: Speed of sound across the BCS–BEC crossover.
figure 4

Solid blue points are found using the raw BA mode frequency and orange diamonds show corrected estimates of cs/vF as k → 0 based on the calculated curvature of the BA mode dispersion at non-zero k/kF (see Supplementary Information). At unitarity, vF = 0.040 m s−1. Also shown are theoretical predictions for cs/vF: BCS theory (black dotted line), Beliaev (black dashed)18, density functional (green dash-dash-dotted)32, Luttinger–Ward (black solid)12, Gaussian fluctuation theory (red dash-dotted)28, and extended T-matrix (purple dash-dot-dotted)30. Inset shows measured BA mode frequency for clouds at different k/kF at unitarity demonstrating linear dispersion. Error bars represent the combined uncertainties in , the fitted ωBA and the angle between the Bragg lasers.

Full size image

By varying the power of our trapping laser, we can tune (and hence k/kF) to map the dispersion of the BA mode. Measured BA mode frequencies for different densities reveal linear dispersion at unitarity in the range 0.45 ≲ k/kF ≲ 0.7 (Fig. 4, inset) with a slope corresponding to cs/vF = 0.36 ± 0.01. At unitarity, as T → 0, where ξ is the Bertsch parameter (ratio of the internal energy of a resonantly interacting Fermi gas to that of an ideal Fermi gas). Our measured value of cs/vF yields ξ = 0.39 ± 0.02 consistent with thermodynamic measurements23.

Focused beam Bragg spectroscopy provides a means to characterize the canonical excitations of homogeneous atomic superfluids that are difficult to access in other systems such as superconductors. This paves the way for studies of elementary excitations in a range of settings, including low-dimensional, lattice-confined and spin–orbit-coupled Fermi gases, as well as finite-temperature phenomena such as pseudogap pairing. By tuning the angle between the Bragg lasers, dynamical properties of strongly correlated quantum gases spanning different momenta can be mapped out providing robust benchmarks for theories of many-body systems.

Data availability.

The data that support the plots in this paper and other findings of this study that are not detailed in the Supplementary Information are available from the corresponding author on request.

Additional Information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.