Mesoscopic Rydberg-blockaded ensembles in the superatom regime and beyond

Abstract

The control of strongly interacting many-body systems enables the creation of tailored quantum matter with complex properties. Atomic ensembles that are optically driven to a Rydberg state provide many examples for this: atom–atom entanglement^1,2, many-body Rabi oscillations³, strong photon–photon interaction⁴ and spatial pair correlations⁵. In its most basic form Rydberg quantum matter consists of an isolated ensemble of strongly interacting atoms spatially confined to the blockade volume—a superatom. Here we demonstrate the controlled creation and characterization of an isolated mesoscopic superatom by means of accurate density engineering and excitation to Rydberg p-states. Its variable size allows the investigation of the transition from effective two-level physics to many-body phenomena. By monitoring continuous laser-induced ionization we observe a strongly anti-bunched ion emission under blockade conditions and extremely bunched ion emission under off-resonant excitation. Our measurements provide insights into both excitation statistics and dynamics. We anticipate applications in quantum optics and quantum information as well as many-body physics experiments.

Main

Rydberg superatoms combine single- and many-body quantum effects in a unique way and have been proposed as fundamental building blocks for quantum simulation and quantum information⁶. Owing to the phenomenon of Rydberg blockade⁷, the ensemble collectively forms a system with only two levels of excitation. Provided a range of interaction larger than the sample size, the presence of one excitation shifts all other atoms out of resonance; therefore only one excitation can be created at a time. Changing the size or the driving conditions restores the underlying many-body nature, and the presence of several excited atoms with pronounced correlations becomes possible. This tunability and the possibility of multiple usage within a single experimental sequence make superatoms a promising complement to single-atom-based quantum technology. It is therefore important to understand the significance of the superatom concept, the implications of its finite spatial extent and its many-body level structure. Here we investigate the latter by measuring the mean Rydberg excitation as well as its time-resolved two-particle correlations in an optically excited, mesoscopic superatom for varying excitation strength and under resonant and non-resonant conditions, revealing very different excitation dynamics.

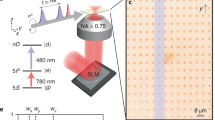
The realization of superatom-based quantum systems requires the implementation of arbitrary arrangements of isolated mesoscopic atomic ensembles in a scalable way. Here we prepare an individual superatom by carefully shaping the density distribution of a Bose–Einstein condensate of ⁸⁷Rb atoms. We first load the condensate into a one-dimensional optical lattice with a spacing of 532 nm, to suppress the axial movement of the atoms. We subsequently compress the atomic sample in the radial direction to reduce its size below the blockade radius and empty all but three (or more) lattice sites using a focused electron beam^8,9,10 (Fig. 1a and Methods). The atom number within the ensemble (N) can be adjusted between 100 and 500 at a temperature of T = (3.5 ± 0.5) μK and the typical size of the sample is ≤3 μm in diameter (Fig. 1b). Our preparation scheme is readily scalable to arrays of superatoms (Fig. 1d).

Figure 1: Preparation of superatoms and excitation level scheme.

a, Starting from a Bose–Einstein condensate in an optical dipole trap with superimposed optical lattice (left) the atoms are radially compressed (middle) and removed from all but a few lattice sites with the help of a focused electron beam (right). b, The resulting—almost spherical—atomic sample contains between 100 and 500 atoms at a temperature of 3–4 μK and dimensions smaller than 3 μm (4σ of a Gaussian fit) in each direction. The axial size of this atomic sample can be varied arbitrarily. c, The superatom is excited with a single-photon transition (λ = 297 nm) into the |51p_3/2〉 state. Effective three-level scheme, comprising the ground state, the singly excited state and the doubly excited state, whose energy has a dependence on r⁻⁶ owing to the van der Waals interaction. Black (blue) arrows denote (off-)resonant excitation and the blockade radius r_B is denoted by the excitation linewidth (grey shaded area). The decay due to ionization and the ion detection are also indicated. R, interatomic distance. d, A one-dimensional array of superatoms, demonstrating the scalability of our approach.

After preparation we excite the atomic ensemble with a single-photon transition from the |5s_1/2〉 ground state to the |51p_3/2, m_j = 3/2〉 Rydberg state at a wavelength of 297 nm with a coupling strength Ω. The single-photon transition circumvents scattering from any intermediate state, therefore allowing a long exposure. The key observable is the string of ions produced by excited atoms that are photoionized by the trap laser¹¹ (with ionization rate Γ_ion = (45 ± 5) kHz). Specifically, we detect the initial peak ion rate as well as the temporal pair correlation function g⁽²⁾(τ), extracted from the time-resolved ion signal (see Methods). The ions continuously emitted from the ensemble lead to a slow decay of the superatom on a timescale between a few milliseconds (see inset Fig. 2) and seconds. Eventually almost 100% of the constituent atoms are converted into ions, of which we detect (40 ± 8)%. For weak resonant driving the superatom mimics an effective two-level system where the excitation of more than one atom is suppressed as a result of blockade. This can be clearly observed in the experiment: Fig. 2 shows pronounced anti-bunching, in good agreement with a theoretical rate model (Methods and Supplementary Information). We extrapolate a value of g⁽²⁾(0) = 0.08 ± 0.06, taking into account an uncorrelated background signal (see Methods). The background constitutes 10–15% of the signal and originates from atoms which are not removed during the preparation of the superatom. The anti-bunching amplitude stays constant during the gradual decay of the superatom, which thus acts as a continuously operating single-ion source¹². The strong suppression of collective oscillations, indicated by the purely exponential shape of g⁽²⁾(τ), shows that the system is in the overdamped regime, where the coherent coupling is overcome by decoherence from the laser linewidth, thermal motion of atoms and residual field fluctuations as well as intrinsic dephasing mechanisms¹³.

Figure 2: Resonant excitation of an isolated superatom.

a, Second-order temporal correlation function of ions emitted from the resonantly excited superatom (Ω/2π = 6 kHz, blue circles). Data points are fitted with an exponential function (blue curve), revealing a value of g⁽²⁾(0) = 0.08 ± 0.06. The black line and the grey shaded area result from a rate model (see Methods and Supplementary Information). The inset shows the data as well as the model curves of the absolute ion rate as a function of time. The integral below both curves is fixed by the total number of ions produced. The bars denote the statistical errors from 1,500 experimental runs.

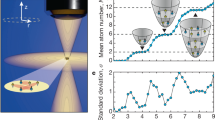
The ability to adjust the size of the atomic sample allows a continuous transition from the superatom limit to a many-body system, where blockade conditions break down. First, this can be used to determine the blockade radius. In Fig. 3a the initial ion rate per atom is shown for increasing axial size l of the sample, keeping the ground-state atom density constant. Under blockade conditions the ion rate first decreases as more and more atoms contribute to the same signal. However, above a critical spatial extent, which we identify with the blockade radius, the ion rate remains constant. The corresponding, independently measured, anti-bunching signal (inset in Fig. 3a) leads to a compatible value of the blockade radius of (2.7 ± 0.8) μm. At first glance it is surprising that we observe blockade at all when we resonantly excite to a p-state. In a p-state the van der Waals interaction is strongly angular dependent (Fig. 3b). For a small interval of θ, the coefficient C₆ is vanishingly small, potentially leading to a breakdown of the overall blockade. Thus, to understand the observed blockade effect we need to go beyond the standard C₆ asymptotics. Figure 3b shows the interaction potential curves for the asymptotic |51p_3/2,3/2, 51p_3/2,3/2〉 pair state, obtained by diagonalization of the interaction Hamiltonian (see Methods). As a result of an avoided crossing with the asymptotic |51p_3/2,1/2, 51p_3/2,1/2〉 pair state, which is energetically separated by an external magnetic field of 35 G, the potential curves which have a negative C₆ coefficient for large distances bend into a repulsive interaction for smaller distances. Thus, the interaction potential for all angles becomes repulsive, enabling an overall blockade.

Figure 3: Blockade radius measurement and theoretical calculations.

a, Initially emitted ion rate per atom for different axial sizes l of the atomic sample (black circles). The density is kept constant for all sample sizes. We determine the effective blockade radius from the intersection of partial linear fits (blue curves). The inset shows the corresponding dependence of g⁽²⁾(0) on l (black circles). The data are compared against a compound theory (red curve) of a hard-shell model (for l ≤ r_B) and a statistical decay The bars indicate the error of the fit for the peak ion rate, the sample size and the initial g⁽²⁾-amplitude. b, Potential curves of the asymptotic |51p_3/2,3/2, 51p_3/2,3/2〉 pair state dependence on the inter-atomic distance R as obtained from diagonalization of the interaction Hamiltonian for equispaced orientation angles from θ = 0 to θ = π/2 (black curves). Red curves indicate the C₆-potentials for θ = 0 and θ = π/2. The grey shaded area denotes the region of resonant excitation for a decoherence rate Γ_d/2π = 340 kHz (see Methods). The green curve and green shaded area show the result of the effective rate model with an effective van der Waals coefficient The inset shows the dependence of C₆ for the asymptotic |51p_3/2,3/2, 51p_3/2,3/2〉 pair state on θ, as obtained from second-order perturbation calculations.

To describe the complex interaction potential structure in an effective but simple way, we assume an isotropic repulsive interaction and solve the many-body problem within an approximate rate equation model with a C₆^eff coefficient as the only free parameter (see Methods). We chose a van der Waals coefficient of to compare the model to the experimental results. The resulting potential curves are indicated by the green shaded area in Fig. 3b. Throughout this paper, we apply the effective model with these parameters to our data and find good agreement over a wide range of laser intensities and detunings.

Our mesoscopic superatom permits inter-atomic distances R of up to ≍3 μm. As a consequence, when the excitation is off-resonant the blockade conditions can be tuned into an anti-blockade¹⁴ and pronounced bunching of the ion emission can be observed (Fig. 4a). We find bunching values of up to g⁽²⁾(0) = 61 ± 8 for large detunings. This behaviour can be understood from the full level structure of the mesoscopic superatom, including excited states with more than one excitation, and is captured well by our rate model: whereas the transition to the first collective Rydberg state is out of resonance, subsequent transitions into doubly excited states are shifted into resonance (Fig. 1c), leading to a cascaded excitation process.

Figure 4: Off-resonant excitation and saturation of a mesoscopic superatom.

a, Pair correlation amplitude g⁽²⁾(0) for different detuning (red circles, bars indicate the error of the fitted initial amplitude), compared against the model results (grey). Inset: g⁽²⁾(τ) for a detuning of Δ/2π = 21 MHz and Ω/2π = 48 kHz (blue circles, bars indicate the statistical error from 600 experimental runs, the solid line is a fit to an exponential decay). b, Dependence of the peak ion rate emitted from the superatom on the coupling strength Ω/2π for resonant excitation (blue circles) and off-resonant excitation with blue detuning of Δ/2π = 4 MHz (black circles) of an ensemble of 125 atoms. Data points are compared against the respective results of the rate model (shaded areas). Dashed lines show continuations of the respective initial quadratic dependence. The vertical bars denote the error of the fit of the ion decay curve, the horizontal bars indicate the intensity fluctuations and drifts of the excitation laser.

The transition of the mesoscopic superatom from an effective two-level system to a complex many-level system is also reflected in its saturation behaviour. In Fig. 4b, we plot the dependence of the initial ion rate on the Rabi frequency for resonant and off-resonant (Δ/2π = 4 MHz) excitation through three orders of magnitude of the experimental parameter Ω. The excitation probability on resonance initially grows quadratically and starts to saturate around an ion rate corresponding to the presence of one excitation. Driving the superatom more strongly, the blockade radius is reduced and above the saturation threshold more excitations can be created, resulting in an increasing initial ion rate—however, with a smaller slope. Thus, the blockade is overcome after saturation has been reached. For off-resonant excitation the signal again shows a quadratic initial slope at a reduced absolute value, but enters a region where the slope is steeper than quadratic, showing a strong enhancement of excitations. For strong enough driving, the resonant and off-resonant excitations eventually reach comparable levels. This happens when the collective coupling strength becomes comparable to the detuning Δ and the difference in the first excitation step for the resonant and off-resonant case disappears. The rate equation model reproduces all experimental findings, despite the major simplifications made. Only for the largest Rabi frequencies in Fig. 4b does the model underestimate the excitation rate. Here, the ensemble Rabi frequency is larger than the decoherence rate and coherent many-body dynamics might become visible. However, a comparison of the rate equation model with a fully quantum-mechanical treatment leads to almost identical predictions for the initial ion rate and g⁽²⁾(0) (Supplementary Information). To observe coherent dynamics requires the condition Ω/Γ_d > 1 and the blockade condition to be satisfied simultaneously. The experiment is thus limited at present to incoherent dynamics. Reducing decoherence is one avenue towards coherent superatom dynamics. An alternative is excitation to higher Rydberg n levels, which increases the interaction.

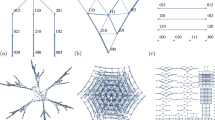
The temporal correlation function g⁽²⁾(τ) also provides insight into the many-body dynamics of the superatom. Figure 5a shows the dependence of the correlation times τ_c of g⁽²⁾(τ) on the detuning. Three different physical regimes can be identified. In Regime I, for large detunings, the atoms spend most of the time in the ground state with small probabilities for single and double excitations. The detection of an ion projects the density matrix onto states with one excitation less. Only doubly excited states emit a second ion and contribute to g⁽²⁾(τ). The correlation time of g⁽²⁾(τ) is thus simply given by the lifetime of the Rydberg excitation. In Regime II, for smaller detunings, we observe a marked slowdown of the relaxation dynamics. In this regime strongly correlated Rydberg aggregates form^15,16. An ionization event projects the system onto a state with increased weight on aggregates of a few excited atoms (Fig. 5b). The relaxation to the steady state is set by the lifetimes of these aggregates, which exceed that of Regime I, as several atoms have to decay. In Region III, on resonance, where anti-bunching occurs, g⁽²⁾(τ) reflects the excitation dynamics after the emission of an ion. The timescale is below 5 μs, shorter than all relevant single-particle timescales, and is therefore a signature of the collectively enhanced excitation rate of the superatom. The corresponding probability distributions are shown in Fig. 5c. Our analysis shows that the temporal pair correlation function is a powerful tool to characterize many-body dynamics and can be used in the future to study quantum phases of driven dissipative systems¹⁷.

Figure 5: Dynamics of the pair correlation function.

a, Dependence of the correlation time τ_c of the pair correlation function on the detuning (same parameters as in Fig. 4a). The black points are the experimental data and the red line is the theoretical prediction. The correlation times are determined by an exponential fit (see Fig. 4a). The bars indicate the error of the fit. The horizontal grey line indicates the lifetime of a Rydberg excitation. The vertical dashed lines demarcate the three physical regimes that can be distinguished (see text). b, Calculated steady-state probability distribution of number of excitations (black bars) and corresponding non-equilibrium distribution after the detection of one ion (blue bars) for Regime II. Temporal evolution back to the steady state is reflected in the correlation time of the pair correlation function. c, Corresponding distributions for Regime III to those in b.

Single superatoms based on collective Rydberg excitations have great potential for applications in quantum optics. They can be used to build high-fidelity photon absorbers¹³ and deterministic ion sources¹². An interaction between multiple superatoms can be realized choosing a Förster resonance, which features a long-range R⁻³ dipole–dipole interaction. The increased interaction then enables us to switch to the coherent collective excitation regime, allowing deterministic state manipulation. Strings of superatoms (see Fig. 1d) are an ideal system for the investigation of energy transfer mechanisms^18,19 and one-dimensional spin systems²⁰. Our approach can be straightforwardly extended to arbitrary patterns of superatoms in two-dimensional lattice systems^8,9. Such quantum systems can then be a resource for further investigations of isotropic and anisotropic long-range interactions²¹, for the quantum simulation of open spin systems^22,23, Bell state measurements^24,25 or interferometric applications^26,27.

Methods

Superatom preparation and laser excitation.

We start with a Bose–Einstein condensate of approximately 1,700 rubidium atoms in a crossed optical dipole trap at a wavelength λ = 1,064 nm. The final trap frequencies are 2π × (180/85/185) Hz. A one-dimensional optical lattice is then superimposed by linearly ramping up a retro-reflected laser beam along the weak axis of the trap and the axial motion is frozen out. Subsequently, the atomic cloud is radially compressed by increasing the intensity of one of the two dipole trap beams. A focused electron beam ((250 ± 100) nm diameter, 20 nA beam current), which is also used to image the sample, removes the atoms from selected areas^8,9,10. In this way, we prepare samples of several hundred atoms with ≤3 μm diameter at a temperature of (3.5 ± 1) μK. After the preparation sequence, a fraction of 10–16% of the atoms reside in the outer regions of the trap.

The superatom is directly excited to a Rydberg state by illuminating it with an ultraviolet laser beam at 297 nm with a waist of 100 μm and a laser power up to 160 mW. The light is produced by frequency doubling a stabilized dye laser (Matisse-DR) in a heated caesium lithium borate (CLBO) crystal installed in a Pound–Drever–Hall stabilized bow-tie cavity. The frequency of the dye laser can be tuned via an offset-locked reference laser, resulting in a relative uncertainty of the ultraviolet frequency of ±0.5 MHz. The linewidth of the excitation light is estimated from dye laser control parameters to less than 200 kHz and the power noise is below 10%.

Electric fields, ion detection and signal processing.

The atomic sample is surrounded by quadruply segmented copper rings of 40 mm diameter at a distance of 25 mm, embodying an octupole electrode configuration²⁸. Applying corresponding voltages, residual electric fields in the chamber are compensated in all directions apart from a remaining permanent vertical component of E₀ ≤ 0.25 V cm⁻¹ that is used to extract the produced ions towards the ion optics below. The ion optics guide the ions into a dynode multiplier (ETP 14553). The signal pulses are further processed with a temporal resolution of 100 ns.

Temporal correlation function.

We numerically calculate the second-order temporal correlation function of the ion signal I(t)

where 〈I(t)I(t + τ)〉 is calculated as the averaged product of counts (0 or 1) in two bins separated by τ and the normalization 〈I(t)〉〈I(t + τ)〉 is given by the averaged ion rate. Several factors affect the data evaluation and have to be taken into account. Artefacts from detector ringing occur for time separations of less then 400 ns. Coulomb repulsion between the ions during time of flight produces further correlations on a timescale which depends on the extraction field. For our parameters, they never occur on timescales longer than 2 μs. We therefore discard all data points with τ ≤ 2 μs. The background atoms (fraction r) contribute an uncorrelated signal to the ion emission of the superatom. This leads to a reduction of the measured amplitude g_meas⁽²⁾ compared to the bare signal from the superatom g_real⁽²⁾, which we correct for: Note that g⁽²⁾(τ) is independent of the detector efficiency.

Calculation of the interaction potential.

The potential curves are calculated by diagonalization of the dipole–dipole interaction Hamiltonian in the presence of an electric and magnetic field. The basis set consists of all pair states which are closer than 15 GHz in energy to the initial |51p_3/2,3/2, 51p_3/2,3/2〉 pair state. We consider all possible combinations of s-, p- and d-states, including all Zeeman levels.

Effective rate model.

The superatom dynamics is described by a Lindblad equation , where and L_ν are the jump operators for ionization (Γ_ion), spontaneous decay into low-lying states which are not ionized (Γ_sp) and decoherence (Γ_d). The decoherence rate represents the cumulative effect of laser linewidth, thermal atomic motion, fluctuating electric fields and intrinsic dephasing mechanisms¹³. The rates of ionization (Γ_ion = 45 kHz) and internal spontaneous decay (Γ_sp = 5 kHz) are known from independent measurements and we extract the excitation rate from the saturation measurements shown in Fig. 4b. For weak driving the ion signal is independent of the interaction term and given by I_Ω≪γ = (Γ_ionN_atoms)/(Γ_ion + Γ_sp)Ω²γ/(γ² + 4Δ²), with γ = Γ_d + Γ_ion + Γ_sp, and N_atoms being the number of atoms within the superatom. Fits to the saturation measurements at Δ = 0 and Δ/(2π) = 4 MHz yield the relation between laser intensity and Ω and the decoherence rate Γ_d/(2π) ≍ 140 kHz and Γ_d/(2π) ≍ 340 kHz, for two different sets of parameters used in the experiment.

Beyond the regime of weak driving we describe the superatom by classical rate equations, which is justified by the large decoherence rate present in our set-up and validated in previous studies of strongly interacting Rydberg systems using such methods^15,29,30. The system of rate equations describes dynamics in classical configuration space, where individual states are connected by single-atom transitions at excitation rate (P_i) and deexcitation rate (D_i). These rates depend on the effective detuning of the atom through P_i = (Ω²γ)/(4δ_i² + γ²) and D_i = (Ω²γ)/(4δ_i² + γ²) + Γ_ion + Γ_sp. The set of many-body rate equations is solved by stochastic sampling of trajectories. Simulations take into account the spatial distribution of atoms as measured in the experiment by averaging over many realizations. Atomic motion is not included within our description and the intricate p-state interaction is approximated with an effective, isotropic van der Waals potential C₆^eff/R⁶.