Did the Minoans understand the Archimedes' spiral more than 1,000 years before him?

A geometrical figure commonly attributed to Archimedes in 300 BC has been identified in Minoan wall paintings dated to over 1,000 years earlier.

The mathematical features of the paintings suggest that the Minoans of the Late Bronze Age, around 1650 BC, had a much more advanced working knowledge of geometry than has previously been recognized, says computer scientist Constantin Papaodysseus of the National Technical University of Athens, Greece, and his colleagues.

The paintings appear in a building that is still being excavated and restored in the ancient Minoan town of Akrotiri on the island of Thera. A catastrophic eruption of the volcano on Thera, now known as Santorini, around 1650 BC, is thought to have dealt a fatal blow to the Minoan culture. The blast covered Akrotiri, on the island's southern coast, in a thick layer of ash that preserved many buildings and artefacts.

Unnatural design

Ten or so buildings have been excavated in Akrotiri so far, including a large one known as Xeste 3, which stands close to the ancient quay. Judging from its large size and extensive wall decorations, Xeste 3 appears to have been some kind of public building, such as a temple or a place for ritual ceremonies.

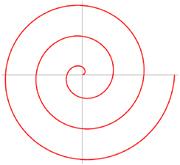
The most impressive feature of the paintings found in Xeste 3 is a series of spirals, each about 32 centimetres in diameter and embellished with dots. Papaodysseus and his team have shown that these are near-perfect Archimedes' spirals: shapes tightly defined by a simple mathematical formula, in which the distance between the windings is constant.

Some spirals, such as the ones found on snail shells, are common in nature. And others can be easily made by unwinding a thread around a central peg. But the Archimedes' spiral is not like either of these. "Seemingly it does not exist in nature," the researchers say.

"This is the earliest time that such advanced geometric figures have been spotted," says Papaodysseus. "The next such figures appear only 1,300 years later." The team report their work in the journal Archaeometry¹.

A feeling for maths

Papaodysseus and his co-workers admit that they cannot know how much the Theran artists actually understood about the geometric principles they used for the paintings, because there aren't any known, translated documents on the subject.

But he says that, at the very least, "experimentation with geometric tools must lie behind the construction of these wall paintings, as well as an impressive feeling for geometry."

Spiral designs in Xeste 3 were first noticed years ago by archaeologists working at the site. But Papaodysseus says that most people previously assumed that the shapes were painted freehand.

His studies suggest that the curves are just too accurate for that: the edges deviate from their strict mathematical form by typically less than a third of a millimetre. Papaodysseus thinks that this precision was probably achieved by the use of stencils, which appear to have been broken up into six parts to make them easier to transport and the paintings easier to fit to a given space.

The key question is how the stencil itself was made.

Splitting a circle

The researchers point out one relatively simple way of constructing such a spiral, without knowing the precise mathematical formula for it. One could divide up a circle using a large number of radial lines with equal angles between them, and a large number of concentric circles. A series of dots moving out one radial line and one concentric circle at a time could be joined together into an Archimedes' spiral. But dividing a circle into more than a dozen equal sections is not a trivial task; try it yourself.

Papaodysseus and his colleagues find that the dots decorating the spirals seem to be positioned almost exactly on the radial lines of circles that are divided into 48 sections.

The wall paintings don't in themselves prove that the Therans knew enough geometry to bisect angles. But it certainly looks that way, says Papaodysseus.

Post a comment to this story by visiting our ancientminoans_centuries.html">newsblog.  

National Technical University of Athens, Greece.

• References

  1. Papaodysseus C., et al. Archaeometry, 48 . 97 - 114 (2006).