Abstract
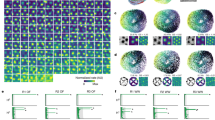
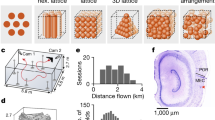
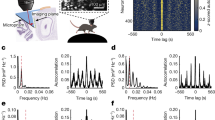
Grid cells provide a neural representation of space, by discharging when an animal traverses through the vertices of a periodic hexagonal grid spanning the environment1. Although grid cells have been characterized in detail in rats1,2,3,4,5,6, the fundamental question of what neural dynamics give rise to the grid structure remains unresolved. Two competing classes of models were proposed: network models, based on attractor dynamics7,8,9, and oscillatory interference models, which propose that interference between somatic and dendritic theta-band oscillations (4–10 Hz) in single neurons transforms a temporal oscillation into a spatially periodic grid10,11,12,13. So far, these models could not be dissociated experimentally, because rodent grid cells always co-exist with continuous theta oscillations4,5,6,14. Here we used a novel animal model, the Egyptian fruit bat15,16, to refute the proposed causal link between grids and theta oscillations. On the basis of our previous finding from bat hippocampus, of spatially tuned place cells in the absence of continuous theta oscillations17, we hypothesized that grid cells in bat medial entorhinal cortex might also exist without theta oscillations. Indeed, we found grid cells in bat medial entorhinal cortex that shared remarkable similarities to rodent grid cells. Notably, the grids existed in the absence of continuous theta-band oscillations, and with almost no theta modulation of grid-cell spiking—both of which are essential prerequisites of the oscillatory interference models. Our results provide a direct demonstration of grid cells in a non-rodent species. Furthermore, they strongly argue against a major class of computational models of grid cells.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Hafting, T., Fyhn, M., Molden, S., Moser, M.-B. & Moser, E. I. Microstructure of a spatial map in the entorhinal cortex. Nature 436, 801–806 (2005)
Sargolini, F. et al. Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science 312, 758–762 (2006)
Barry, C., Hayman, R., Burgess, N. & Jeffery, K. J. Experience-dependent rescaling of entorhinal grids. Nature Neurosci. 10, 682–684 (2007)
Langston, R. F. et al. Development of the spatial representation system in the rat. Science 328, 1576–1580 (2010)
Wills, T. J., Cacucci, F., Burgess, N. & O’Keefe, J. Development of the hippocampal cognitive map in preweanling rats. Science 328, 1573–1576 (2010)
Boccara, C. N. et al. Grid cells in pre- and parasubiculum. Nature Neurosci. 13, 987–994 (2010)
Fuhs, M. C. & Touretzky, D. S. A spin glass model of path integration in rat medial entorhinal cortex. J. Neurosci. 26, 4266–4276 (2006)
McNaughton, B. L., Battaglia, F. P., Jensen, O., Moser, E. I. & Moser, M.-B. Path integration and the neural basis of the ‘cognitive map’. Nature Rev. Neurosci. 7, 663–678 (2006)
Burak, Y. & Fiete, I. R. Accurate path integration in continuous attractor network models of grid cells. PLOS Comput. Biol. 5, e1000291 (2009)
Burgess, N., Barry, C. & O’Keefe, J. An oscillatory interference model of grid cell firing. Hippocampus 17, 801–812 (2007)
Giocomo, L. M., Zilli, E. A., Fransén, E. & Hasselmo, M. E. Temporal frequency of subthreshold oscillations scales with entorhinal grid cell field spacing. Science 315, 1719–1722 (2007)
Hasselmo, M. E., Giocomo, L. M. & Zilli, E. A. Grid cell firing may arise from interference of theta frequency membrane potential oscillations in single neurons. Hippocampus 17, 1252–1271 (2007)
Blair, H. T., Welday, A. C. & Zhang, K. Scale-invariant memory representations emerge from Moiré interference between grid fields that produce theta oscillations: a computational model. J. Neurosci. 27, 3211–3229 (2007)
Hafting, T., Fyhn, M., Bonnevie, T., Moser, M.-B. & Moser, E. I. Hippocampus-independent phase precession in entorhinal grid cells. Nature 453, 1248–1252 (2008)
Yovel, Y., Falk, B., Moss, C. F. & Ulanovsky, N. Optimal localization by pointing off axis. Science 327, 701–704 (2010)
Ulanovsky, N. & Moss, C. F. What the bat’s voice tells the bat’s brain. Proc. Natl Acad. Sci. USA 105, 8491–8498 (2008)
Ulanovsky, N. & Moss, C. F. Hippocampal cellular and network activity in freely moving echolocating bats. Nature Neurosci. 10, 224–233 (2007)
Ulanovsky, N. & Moss, C. F. Dynamics of hippocampal spatial representation in echolocating bats. Hippocampus 21, 150–161 (2011)
Wilson, M. A. & McNaughton, B. L. Dynamics of the hippocampal ensemble code for space. Science 261, 1055–1058 (1993)
Chrobak, J. J. & Buzsáki, G. High-frequency oscillations in the output networks of the hippocampal-entorhinal axis of the freely behaving rat. J. Neurosci. 16, 3056–3066 (1996)
Buzsáki, G. Theta oscillations in the hippocampus. Neuron 33, 325–340 (2002)
Stewart, M. & Fox, S. E. Hippocampal theta activity in monkeys. Brain Res. 538, 59–63 (1991)
Ekstrom, A. D. et al. Human hippocampal theta activity during virtual navigation. Hippocampus 15, 881–889 (2005)
Witter, M. P., Wouterlood, F. G., Naber, P. A. & Van Haeften, T. Anatomical organization of the parahippocampal-hippocampal network. Ann. NY Acad. Sci. 911, 1–24 (2000)
Solstad, T., Boccara, C. N., Kropff, E., Moser, M.-B. & Moser, E. I. Representation of geometric borders in the entorhinal cortex. Science 322, 1865–1868 (2008)
Deshmukh, S. S., Yoganarasimha, D., Voicu, H. & Knierim, J. J. Theta modulation in the medial and the lateral entorhinal cortices. J. Neurophysiol. 104, 994–1006 (2010)
Mizuseki, K., Sirota, A., Pastalkova, E. & Buzsáki, G. Theta oscillations provide temporal windows for local circuit computation in the entorhinal-hippocampal loop. Neuron 64, 267–280 (2009)
Brandon, M. P. et al. Reduction of theta rhythm dissociates grid cell spatial periodicity from directional tuning. Science 332, 595–599 (2011)
Koenig, J., Linder, A. N., Leutgeb, J. K. & Leutgeb, S. The spatial periodicity of grid cells is not sustained during reduced theta oscillations. Science 332, 592–595 (2011)
Hansel, D. & Sompolinsky, H. Modeling feature selectivity in local cortical circuits. In Methods in Neuronal Modeling: from Synapses to Networks 2nd edn (eds Kock, C. & Segev, I. ) 499–567 (MIT Press, 1998)
Acknowledgements
We thank D. Derdikman, S. Romani, M. Ahrens and Y. Cohen for comments on the manuscript, M. Melcón for initial assistance with hippocampal CA1 recordings, M. Weinberg for veterinary oversight, and R. Eilam and C. Ra'anan for histology. This study was supported by research grants from the Israel Science Foundation and Minerva Foundation to N.U., by a Lev-Zion predoctoral excellence fellowship to M.M.Y., as well as by grants from the Norwegian Research Council and the Kavli Foundation to M.P.W.
Author information
Authors and Affiliations
Contributions
M.M.Y. and N.U. designed the study, conducted the experiments, analysed the data and wrote the manuscript. M.P.W. performed immunohistochemical analyses, delineated the anatomical structures in the hippocampus and entorhinal cortex of Egyptian fruit bats, and verified recording sites. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
The file contains Supplementary Figures 1-22 with legends, Supplementary Methods, Supplementary Text and Data and additional references. (PDF 18634 kb)
Rights and permissions
About this article
Cite this article
Yartsev, M., Witter, M. & Ulanovsky, N. Grid cells without theta oscillations in the entorhinal cortex of bats. Nature 479, 103–107 (2011). https://doi.org/10.1038/nature10583
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature10583
This article is cited by
-
A spatial transformation-based CAN model for information integration within grid cell modules
Cognitive Neurodynamics (2024)
-
Mobile cognition: imaging the human brain in the ‘real world’
Nature Reviews Neuroscience (2023)
-
Contextual and pure time coding for self and other in the hippocampus
Nature Neuroscience (2023)
-
Neural Correlates of Spatial Navigation in Primate Hippocampus
Neuroscience Bulletin (2023)
-
Grid cell modeling with mapping representation of self-motion for path integration
Neural Computing and Applications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.