Abstract
A meta-atom platform providing decoupled tuning for the constitutive wave parameters remains as a challenging problem, since the proposition of Pendry. Here we propose an electromagnetic meta-atom design of internal anisotropy (εr ≠ εθ), as a pathway for decoupling of the effective- permittivity εeff and permeability μeff. Deriving effective parameters for anisotropic meta-atom from the first principles, and then subsequent inverse-solving the obtained decoupled solution for a target set of εeff and μeff, we also achieve an analytic, top-down determination for the internal structure of a meta-atom. To realize the anisotropy from isotropic materials, a particle of spatial permittivity modulation in r or θ direction is proposed. As an application example, a matched zero index dielectric meta-atom is demonstrated, to enable the super-funneling of a 50λ-wide flux through a sub-λ slit; unharnessing the flux collection limit dictated by the λ-zone.
Similar content being viewed by others
Introduction
Electromagnetic metamaterials exhibiting naturally non-occurring refractive indices1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24 and their application to exotic forms of wave manipulation25,26,27,28,29 have become one of the hottest research topics. Because electromagnetic metamaterials manifest their properties through electromagnetic couplings to the far-field, design strategies have been focused on the realization of designer electric (εeff) and magnetic (μeff) dipolar responses, with the engineering and assembly of metallic or dielectric building blocks. Nonetheless, in most cases, the realization of exotic εeff and μeff has been achieved via the simple combination of elementary resonators in a non-isotropic and polarization-dependent form1,2,25, at the same time based on retro-fit, bottom-up approaches - where the building blocks are initially proposed and the subsequent design is carried out through a series of iterations and guesswork.
Meanwhile, although the decoupling of those fundamental constitutive wave parameters has been envisaged as an ideal platform toward the top-down and deterministic design of the metamaterial (Pendry et al.26), its feasibility has not been treated until recently. With the presence of inherent cross-coupling terms between constitutive parameters (as shown for εeff and μeff in electromagnetics3, or  and ρeff in acoustics30), it is not always straightforward to achieve the decoupling of wave parameters. Elastic metamaterial for decoupling of density and stiffness in positive31 or negative32 parameter regime, sub skin-depth metallic particles of decoupled permittivity and permeability for positive high refractive index4,5, and lastly the acoustic omni meta-atom30 addressing the octant space of wave parameters have been demonstrated; yet existence of the meta-atom platforms which could access both positive and negative values of parameters, in the general spectrum of electromagnetic wave is not evident at this stage. Moreover, we note that the design of electromagnetic metamaterial has been largely based on metallic inclusions of well-defined current paths, meanwhile the intrinsic loss of metals makes dielectric metamaterial1,6,7,8,9,10 a more favorable option.
and ρeff in acoustics30), it is not always straightforward to achieve the decoupling of wave parameters. Elastic metamaterial for decoupling of density and stiffness in positive31 or negative32 parameter regime, sub skin-depth metallic particles of decoupled permittivity and permeability for positive high refractive index4,5, and lastly the acoustic omni meta-atom30 addressing the octant space of wave parameters have been demonstrated; yet existence of the meta-atom platforms which could access both positive and negative values of parameters, in the general spectrum of electromagnetic wave is not evident at this stage. Moreover, we note that the design of electromagnetic metamaterial has been largely based on metallic inclusions of well-defined current paths, meanwhile the intrinsic loss of metals makes dielectric metamaterial1,6,7,8,9,10 a more favorable option.
Here, we propose a new platform for electromagnetic metamaterial: a meta-atom of decoupled constitutive parameters, enabling top-down design - where the target εeff and μeff are first specified and the design parameters are subsequently determined, all the while using readily available lossless dielectrics. We first analytically solve the problem of decoupled effective- permittivity εeff and permeability μeff, by introducing a hypothetical meta-atom of internal anisotropic susceptibility χr ≠ χθ; for their axis are set in conform to the electric- and magnetic- characteristic movements of the electron, or equivalently to their corresponding dipole moments pr (χr) and mz (χθ) (Fig. 1). We then realize top-down design for the internal structure of a meta-atom, by inversely-solving the decoupled equation to get the required χr and χθ (or εr and εθ) for targeted εeff and μeff. Finally, a meta-atom implementation based on isotropic materials of spatial (r, θ) permittivity modulation is proposed to realize the required (εr, εθ) for a matched zero index, along with the demonstration of the super-funneling for a 50λ-wide flux through a sub-λ slit.
Results
Structure of the meta-atom for decoupled permittivity and permeability
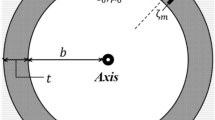
We consider the two dimensional problem shown in Fig. 2(a); where a transverse electric (TE) plane wave is incident onto a cylindrical particle of radius R with split εr, εθ anisotropy. To derive εeff and μeff, we start from the zeroth order expressions for the electric and magnetic polarizabilities (αe and αm)11 of the isolated particle,
(a) Schematic of the anisotropic meta-atom illuminated by TE plane wave. (b) Charge and (c) current distribution at the electric and magnetic resonance frequencies, respectively (arrows denote current flow). (d) Calculated εr and εθ values that give matched zero index property (solid: R = 0.4a, dashed: R = 0.45a). (e) εeff and μeff tunability including demonstration of matched index property (neff = ±0.1).

where εy and εθ being the permittivity of the particle along the y and θ direction respectively, and the integration is taken over the particle cross section C. It is noted that in Eq. (1) we treat only the dipole polarizability terms, with an implicit assumption of long-wavelength approximation. Solving the wave equation in polar coordinate for the general solution of E and H (details in Supplementary Information), and then keeping only the lowest order terms (within good approximation under εr, εθ ≫ 1), we achieve analytical solutions for αe and αm,

where ϕk = k0R and bn being the coefficients of Bessel-Fourier expansions [Supplementary Eq. (S3)].
From αe and αm of the isolated particle (2), it is then straightforward to calculate εeff and μeff for a square lattice of meta-atoms. Using the mixing formula12 we arrive,

where  and
and  are the dynamic interaction constants with periodicity a, and a lattice point vector rI12.
are the dynamic interaction constants with periodicity a, and a lattice point vector rI12.
Inspection of Eqs (2) and (3) clearly shows the dependence of μeff only on εθ, or complete decoupling of μeff (or αm) from εr, which supports separate tunability of εeff and μeff from the adjustment of εr and εθ; confirming the proposed ansatzs based on anisotropic susceptibility in relation to the respective current patterns exhibited by the electric and magnetic modes [Figs 1 and 2(b,c)]. Because the obtained decoupling condition αe(εr, εθ) and αm(εθ) are based on (2) - which are expanded from (1), the condition of decoupling becomes to follow the generic constraint of long-wavelength approximation in metamaterial applications; lattice period (a)/wavelength (λ/neff) ~ 1/10. For example, with a = 5λ, the validity of our approximation would hold till |neff| < 0.5. We also note, Eq. (3) works well in the low index regime (neff ≪ λ/2a12), while εeff and μeff of high values also always can be determined from S-matrix parameters13.
Focusing here on the low index case, we now proceed to inverse-solve the problem of (3), in order to determine required εr (αe) and εθ (αe, αm) by using (2), from target εeff and μeff. Meanwhile the complete solution with Bessel-Fourier series (Supplementary Eq. (S3)) can also be used, here we show the simpler form of first-order approximated solution, near the first zeros of the Bessel functions11 (see Supplementary Information for details). For example, by specifying target εeff and μeff equal to 0, we arrive to a set of simple and intuitive relations which are used to calculate the required values of εr and εθ for the matched zero index;

where A0(ϕk) = A(εeff = 0; ϕk) and B0(ϕk) = B(μeff = 0; ϕk) are slowly-varying functions of ϕk (Supplementary Eq. (S6) and Supplementary Fig. S1), and α0 (~2.405), α1 (~3.831) are the first zeros of the zeroth and first order Bessel functions. Again, for a given particle radius and frequency ϕk = k0R, the achievement of μeff = 0 from the single parameter εθ is evident from B(μeff = 0; ϕk) in Eq. (4). Subsequent realization of εeff = 0 from the determination of εr is made then using A(εeff = 0; ϕk) in (4). In Fig. 2(d) we show the solution obtained with Supplementary Eq. (S5), giving the values of (εr, εθ) that support a matched zero index at different target frequencies; for the particles of normalized radius R = 0.4a (solid lines) and 0.45a (dashed lines), of periodicity (a). The required (εr, εθ) value set depends on the frequency and particle size, and get smaller as either f or R increase. We also demonstrate in Fig. 2(e) the tunability of εeff and μeff by addressing matched index properties at neff = ±0.1, again, with the use of (3). It is worth to note that in all cases, the required εr is greater than εθ, red-shifting the usually higher energy electric dipole resonance (εr, εθ) closer toward the lower energy magnetic dipole resonance (εθ).
Dielectric implementation of the anisotropic meta-atom
To realize the set of required εr and εθ from isotropic materials, we spatially modulate the permittivity inside the particle along a given axis (r or θ). A proposed structure of nano-pizza cross-section is shown in Fig. 3(a). Extending the concept of average permittivity33 from Gauss’ law in polar coordinates we obtain,
Anisotropic meta-atoms (εr ≠ εθ) of nano-pizza cut geometry with (a) 40 slices and (b) 8 slices. (inset in (a) shows an example of nano-donut). Calculated εeff and μeff for meta-atoms lattice of radius (c) R = 0.4a (a = 1.5 cm), and (d) R = 0.45a (a = 600 nm). By appropriate choice of a, the operating frequency is determined. Circles indicate the frequencies of operation at matched zero index and horizontal dashed lines indicate εeff = 0 and μeff = 0. Excellent agreement between the theory and numerical results (for both 40 slice and 8 slice implementations), especially near the matched zero index, are observed.

where ε1, ε2 (ε1 < ε2) are the permittivities of constituent dielectrics shown in Fig. 3(a), and p is the fill factor of slices containing ε2. While it is also possible to design the meta-atom for fixed ε1 (1, for example) by changing p and ε2, we here focus on the case of fill factor p = 0.5, without any loss of generality (design example with p = 0.83, for ε1 = 1 (air) and ε2 = 12.25 (silicon) is shown in the Supplementary Information). On the other hand, as the arithmetic mean is always larger than the harmonic mean in (5), the condition of εr ≥ εθ for matched zero index realization [Fig. 2(d)] is only met with nano-pizza cross-section geometry [we note, εθ ≥ εr for the nano-donut cross-section - inset of Fig. 3(a)]. Using (5) for the pair (εr, εθ) = (166, 31.1) [giving zero index at f = 0.212 c/a (4.24 GHz for a = 1.5 cm) and R = 0.4a from Fig. 2(d)], we obtain (ε1, ε2) = (16.32, 315.8).
In Fig. 3(c) we show plots of εeff (αe) and μeff (αm) obtained from Eq. (3), with αe and αm analytically obtained from Eq. (2) (solid lines), and also numerically obtained using Eq. (1) (solid dots) from the result of finite difference time domain simulations of a 40-slice structure. Near the zero-index, an almost perfect fit with less than 1% frequency error was obtained from that predicted by Supplementary Eq. (S5). In consideration of fabrication complexity, a structure with reduced number of slices has also been tested [Fig. 3(b)]. Even though the calculation of (εr, εθ) from (p; ε1, ε2) started to deviate from Eq. (5) when the size of slices was increased, it was still possible to determine (ε1, ε2) = (15.12, 171.9) providing a matched zero index for the 8-slice structure at f = 0.212 c/a [marked with ‘+’ symbol in Fig. 3(c)], by using few Newton iterations for the zero-index frequency deviation. It is noted that this value determined from the mixing formula (3) is in excellent agreement with exact values of (ε1, ε2) = (14.53, 179.2) extracted from S-matrix parameters13.
It is emphasized that, experimentally available, smaller permittivity values using Si and SiO2 for example [40 slices: (ε1, ε2) = (2.43, 15.13), 8 slices: (2.22, 12.96)], can be readily accessed by increasing the radius R of the particle to 0.45a, to give matched zero index at f = 0.546 c/a (e. g., λ = 1100 nm for a = 600 nm) [Fig. 3(d)]. The designs with 2D-slab structure (of height = 2λ, at GHz operation frequency) and a void at the particle center region are also discussed in Supplementary Information and Figures.
Realization of the zero index super funneling through a subwavelength slit
Using the matched zero index, we now investigate the problem of extraordinary optical transmission (EOT)34,35,36,37,38, for which the maximum field enhancement is limited by the λ-zone34. Applications of zero index tunneling have been demonstrated in the past11,14,15,16, yet the possibility of EOT beyond the λ-zone has not been investigated. A perfect electric conductor (PEC) having sub-wavelength (0.21λ) slit, of flux reception width far larger (17λ) than the λ-zone has been tested, with the application of single-layer matched zero index meta-atoms (εeff = μeff = 0, f = 0.212 c/a) covering the input/output regions of PEC. It is important to note that the tuning of meta-atom near the slit gap is necessary since the effective medium theory starts to deviates with the introduction of the metal slit in the meta-atom array, breaking the periodicity of the lattice. The detailed tuning procedure is described in the Supplementary Information. The transmittance of the matched zero-index meta-atom nanoslit shows almost perfect transmittance of 0.97 [Fig. 4(a,d)], a ~50 times increase compared to the slit without zero-index meta-atom coating [Fig. 4(a,e)]; demonstrating the super-funneling of flux which is 17 times greater than the λ-zone. A low-index 8-slice structure [(ε1, ε2) = (2.22, 12.96) at R = 0.45a providing matched zero index at f = 0.546 c/a, see Fig. 3(d)] over much larger flux reception area (50λ) also has been tested, to compensate for a factor of ~90 channel width variation (50λ to 0.55λ). A transmittance of 0.85 was achieved, showing the super-funneling of 42λ-flux (50λ · 0.85) through the meta-atom coated slit [Fig. 4(a,f)].
(a) Transmission spectra of the slit; without (green) and with matched zero-index meta-atom array of (blue) high index (ε1, ε2) = (14.53, 179.2) and (red) low index (2.22, 12.96) materials. f0 is the frequency of matched zero index. (b,c) Ex field pattern near the nanoslit at f0; (b) with and (c) without the zero-index meta-atom array. The near field pattern shows the associated dramatic enhancement of the electric field with the coating of matched zero index meta-atoms. (d–f) Hz field pattern of the slit at f0 (d) without, (e) with high-index, and (f) with low-index meta-atom array. Slit width; 0.21λ (d,e) and 0.55λ (f).
Discussion
To summarize, a hypothetical meta-atom of internal (r, θ) anisotropy has been proposed. Introducing the split- symmetry of susceptibility χr ≠ χθ conforming to the orthogonal axes of current pathways of the respective electric- and magnetic- dipoles, we show analytically the decoupling and separate tunability of εeff and μeff. The desired target optical response εeff and μeff are provided by top-down, analytically determined εr and εθ values, which are readily achieved with conventional isotropic materials in radial- or angular- anisotropic spatial arrangements. We note that, our approach widens the scope of metamaterial design; offering a top-down optical response (including both matched zero and negative index) from lossless dielectrics, meanwhile lifting the stringent restrictions of accidental degeneracy6 which itself was limited to matched zero index at fixed frequency. In an application to EOT, utilizing a single layer of matched zero index meta-atoms, we demonstrated for the first time a super-funneling of electromagnetic flux, overcoming the usual λ-zone limit by two orders. Our proposal of coordinate-conforming anisotropy for decoupling the electric and magnetic responses and thus the separate control of εeff and μeff should be applicable to elementary resonators in other exotic coordinate systems compliant to current pathways of chosen electric/magnetic resonances. We expect future development of other anisotropic meta-atom families based on our approach.
Additional Information
How to cite this article: Koo, S. et al. Top-down, decoupled control of constitutive parameters in electromagnetic metamaterials with dielectric resonators of internal anisotropy. Sci. Rep. 7, 42447; doi: 10.1038/srep42447 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Ahmadi, A. & Mosallaei, H. Physical configuration and performance modeling of all-dielectric metamaterials. Phys. Rev. B 77, 045104 (2008).
Zhang, S. et al. Near-infrared double negative metamaterials. Opt. Express 13, 4922–4930 (2005).
Alù, A. First-principles homogenization theory for periodic metamaterials. Phys. Rev. B 84, 075153 (2011).
Kim, J. Y. et al. Highly tunable refractive index visible-light metasurface from block copolymer self-assembly. Nat. Commun. 7, 12911 (2016).
Chung, K., Kim, R., Chang, T. & Shin, J. Optical effective media with independent control of permittivity and permeability based on conductive particles. Appl. Phys. Lett. 109, 021114 (2016).
Huang, X., Lia, Y., Hang, Z. H., Zheng H. & Chan, C. T. Dirac cones induced by accidental degeneracy in photonic crystals and zero-refractive-index materials. Nat. Materials 10, 582–586 (2011).
Li, Y. et al. On-chip zero-index metamaterials. Nat. Photon. 9, 738–742 (2015).
Zhao, Q., Zhou, J., Zhang, F. & Lippens, D. Mie resonance-based dielectric metamaterials. Mater. Today 12, 60–69 (2009).
Soukoulis, C. M. & Wegener, M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat. Photonics 5, 523–530 (2011).
Vendik, I. B., Vendik, O. G. & Gashinova, M. S. Artificial dielectric medium possessing simultaneously negative permittivity and magnetic permeability. Tech. Phys. Lett. 32, 429–433 (2006).
Silveirinha, M. & Engheta, N. Design of matched zero-index metamaterials using nonmagnetic inclusions in epsilon-near-zero media. Phys. Rev. B 75, 075119 (2007).
Silveirinha, M. G. Nonlocal homogenization model for a periodic array of ε-negative rods. Phys. Rev. E 73, 046612 (2006).
Smith, D. R., Schultz, S., Markoš, P. & Soukoulis, C. M. Determination of effective permittivity and permeability of metamaterials from reflection and transmission coefficients. Phys. Rev. B 65, 195104 (2002).
Edwards, B., Alủ, A., Young, M. E., Silveirinha, M. & Engheta, N. Experimental Verification of Epsilon-Near-Zero Metamaterial Coupling and Energy Squeezing Using a Microwave Waveguide. Phys. Rev. Lett. 100, 033903 (2008).
Cheng, Q., Liu, R., Huang, D., Cui, T. J. & Smith, D. R. Circuit verification of tunneling effect in zero permittivity medium. Appl. Phys. Lett. 91, 234105 (2007).
Silveirinha, M. & Engheta, N. Tunneling of electromagnetic energy through subwavelength channels and bends using ε-near-zero materials. Phys. Rev. Lett. 97, 157403 (2006).
Shalaev, V. M. Optical negative-index metamaterials. Nat. Photonics 1, 41–48 (2007).
Choi, M. et al. A terahertz metamaterial with unnaturally high refractive index. Nature 470, 369–373 (2011).
Alủ, A. & Engheta, N. The quest for magnetic plasmons at optical frequencies. Opt. Express 17, 5723–5730 (2009).
Alủ, A., Salandrino, A. & Engheta, N. Negative effective permeability and left-handed materials at optical frequencies. Opt. Express 14, 1557–1567 (2006).
Vallecchi, A., Albani, M. & Capolino, F. Collective electric and magnetic plasmonic resonances in spherical nanoclusters. Opt. Express 19, 2754–2772 (2011).
Mirin, N. A. & Halas, N. J. Light-bending nanoparticles. Nano Lett. 9, 1255–1259 (2009).
Ginzburg, P., Berkovitch, N., Nevet, A., Shor, I. & Orenstein, M. Resonances On-Demand for Plasmonic Nano-Particles. Nano Lett. 11, 2329–2333 (2011).
Plum, E. et al. Metamaterial with negative index due to chirality. Phys. Rev. B 79, 035407 (2009).
Schurig, D. et al. Metamaterial Electromagnetic Cloak at Microwave Frequencies. Science 314, 977–980 (2006).
Pendry, J. B., Schurig, D. & Smith, D. R. Controlling electromagnetic fields. Science 312, 1780–1782 (2006).
Chen, H., Chan, C. T. & Sheng, P. Transformation optics and metamaterials. Nat. Materials 9, 387–396 (2010).
Genov, D. A., Zhang, S. & Zhang, X. Mimicking celestial mechanics in metamaterials. Nat. Physics 5, 687–692 (2009).
Li, J. & Pendry, J. B. Hiding under the carpet: a new strategy for cloaking. Phys. Rev. Lett. 101, 203901 (2008).
Koo, S., Cho, C., Jeong, J.-H. & Park, N. Acoustic omni meta-atom for decoupled access to all octants of a wave parameter space. Nat. Commun. 7, 13202 (2016).
Bückmann, T. et al. An elasto-mechanical unfeelability cloak made of pentamode metamaterials. Nat. Commun. 5, 4130 (2014).
Oh, J. H., Kwon, Y. E., Lee, H. J. & Kim, Y. Y. Elastic metamaterials for independent realization of negativity in density and stiffness. Sci. Rep. 6, 23630 (2016).
Hu, F.-G., Song, J. & Kamgaing, T. Modeling of multilayered media using effective medium theory. EPEPS, IEEE 19th Conference on 225–228 (2010).
Kang, J. H., Kim, D. S. & Park, Q.-H. Local capacitor model for plasmonic electric field enhancement. Phys. Rev. Lett. 102, 093906 (2009).
Seo, M. A. et al. Terahertz field enhancement by a metallic nano slit operating beyond the skin-depth limit. Nat. Photon. 3, 152–156 (2009).
Koo, S., Kumar, M. S., Shin, J., Kim, D. & Park, N. Extraordinary magnetic field enhancement with metallic nanowire: role of surface impedance in Babinet’s principle for sub-skin-depth regime. Phys. Rev. Lett. 103, 263901 (2009).
García-Vidal, F. J., Moreno, E., Porto, J. A. & Martín-Moreno, L. Transmission of light through a single rectangular hole. Phys. Rev. Lett. 95, 103901 (2005).
Seo, M. A. et al. Active terahertz nanoantennas based on VO2 phase transition. Nano Lett. 10, 2064–2068 (2010).
Acknowledgements
This study was supported by the National Research Foundation funded by the Ministry of Science, ICT and Future Planning (Global Frontier Program: No. NRF-2014M3A6B3063708 and Global Research Laboratory: No. NRF-2008-00580).
Author information
Authors and Affiliations
Contributions
S.K. devised the structure of meta-atom and performed the theoretical deviation, and numerical analysis. N.P. conceived the idea for the top-down design of meta-atom structure, and encouraged S.K. to develop analytical model. D.M., N.P. and Y.K. checked the theoretical deviations, reviewed the manuscript, and wrote the manuscript with S.K.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Koo, S., Mason, D., Kim, Y. et al. Top-down, decoupled control of constitutive parameters in electromagnetic metamaterials with dielectric resonators of internal anisotropy. Sci Rep 7, 42447 (2017). https://doi.org/10.1038/srep42447
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep42447
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.