Abstract
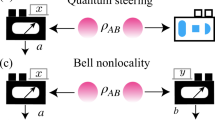
Temporal steering is a form of temporal correlation between the initial and final state of a quantum system. It is a temporal analogue of the famous Einstein-Podolsky-Rosen (spatial) steering. We demonstrate, by measuring the photon polarization, that temporal steering allows two parties to verify if they have been interacting with the same particle, even if they have no information about what happened with the particle in between the measurements. This is the first experimental study of temporal steering. We also performed experimental tests, based on the violation of temporal steering inequalities, of the security of two quantum key distribution protocols against individual attacks. Thus, these results can lead to applications for secure quantum communications and quantum engineering.
Similar content being viewed by others
Introduction
Einstein-Podolsky-Rosen (EPR) steering refers to strong nonclassical nonlocal bipartite correlations. It was first described by Schrödinger1 as a generalization of the EPR paradox2. The recent celebration of the 80 years of steering and the EPR paradox3 showed that our understanding of this phenomenon is now much deeper, but still very limited. Steering differs from quantum entanglement4 and Bell nonlocality5,6,7, as not every entangled state manifests steering and not every state that manifests steering violates Bell’s inequality8. In other words, steerable states are a subset of entangled states and a superset of Bell nonlocal states. Analogously to Bell nonlocality, steering can be detected independently of other nonclassical correlations by simple inequalities8,9,10 that can include as little as two measurements with two outcomes for Alice and a set of four possible states for Bob9. Such inequalities were tested in several experiments10,11,12,13,14,15,16,17, including a recent loophole-free experiment18. Steering can be interpreted as a correlation between two systems (measuring devices), where only one of them is trusted. This property shows an operational meaning of steering and indicates its potential applications in quantum cryptography and quantum communication, e.g., for entanglement distribution8,19. Steering-based protocols can provide secure communications even when only one party trusts its devices. Such protocols are easier to implement than completely-device-independent protocols20, but are more secure than standard protocols requiring mutual trust between the communicating parties.
Temporal steering21 (TS), analogously to EPR steering, is observed when Alice can steer Bob’s state into one of two orthogonal states by properly choosing her measured observable. Despite this similarity, the implications of these temporal and spatial phenomena are fundamentally different. To detect TS21, Alice and Bob perform consecutive measurements (using a random sequence of mutually-unbiased bases known only to them) on the same system to test temporal correlations between its initial and final states. Breaking the temporal steering inequality, given in ref. 21, implies that no unauthorised party can gather full information about the final quantum state. In other words, there was no quantum collapse and the observed correlations are stronger than any correlations between the initial state and its classical copy prepared by measuring and resending the initial state. Such strong temporal correlations must have a quantum origin. Their stronger form asserts that no third party can gather more information about the original state than Bob. In this case, Alice and Bob witness temporal correlations of a unique strength, which prove that they interact with the original quantum system and not with one of its quantum copies. This unique relation between the past and the future is referred to here as monogamous quantum causality. Here, Alice mostly steers the future state of Bob and no other system can be steered with the same strength. This regime is especially interesting for quantum cryptography, because it allows performing secure quantum key distribution protocols over a quantum channel, which is not fully characterised (trusted).
In contrast with EPR steering10,11,12,13,14,15,16,17,18,22,23,24,25,26,27,28,29,30, TS has not yet been investigated experimentally. This article reports, to our knowledge, the first experimental demonstration of TS. We verify, in a quantum linear-optical experiment, the relation between TS and two quantum key distribution (QKD) protocols based on mutually unbiased bases (MUB). Specifically, we apply temporal steering for experimental testing the security of the Bennett-Brassard 1984 protocol (BB84)31 and the six-state 1998 protocol by Bruss (B98)32 against individual attacks. As discussed theoretically in ref. 33, the unconditional security of these protocols34,35,36 (even against individual attacks) implies the existence of a kind of monogamous temporal correlations. The first experimental test of this temporal steering monogamy is reported here.
TS is understood as the ability of Alice to prepare a quantum object in a quantum state that after travelling, for a period of time through a damping channel, to Bob will manifest strong temporal correlations between its initial and final states. These correlations tell us how strong is the influence of Alice’s choice of observable on Bob’s results. The channel can erase partially or completely Alice’s influence. This decoherence process will take some time. Thus, TS is an appropriate name for this effect. It was shown21 that these temporal correlations are related to the one-way security bound in BB84. Therefore, this new kind of steering, similarly as the standard EPR steering, can be responsible for secure (one-way) quantum communications. However, ref. 21 did not explain the origins of this relation between TS and QKD. In a certain sense, this TS is a kind of one-way (or asymmetric) (temporal) steering because of the time arrow. For spatial steering, one could consider one-way (spatial) steering as well as two-way (spatial) steering, where the roles of Alice and Bob are interchanged. For TS this can be done only for a unitary (reversible) evolution of a given steered system. Steering is, by definition, asymmetric, as corresponding to one-side device-independent entanglement detection. Thus, in steering one assumes that only one side is performing faithful measurements. This is in contrast with entanglement, where both parties are trusted, as well as Bell’s nonlocality, where both parties are untrusted.
Temporal steering
In our experiment, Alice with probability P(a|Ai) prepares qubits by rotating |H〉 (a horizontally-polarised photon) to one of the six eigenstates of the Pauli operators. This is done by the consecutive use of half- (H) and quarter-wave (Q) plates as shown in Fig. 1. To implement BB84, Alice sends eigenstates of only the σ1 and σ2 operators. She implements B98 by including also σ3. This method of state preparation is equivalent to performing a projective nondestructive measurement Ai by separating states of a = +1 and a = −1 with a polarising beam splitter (an equivalent of the Stern-Gerlach experiment37), and detecting their presence in one of its paths. A photon with probability P(+1|Ai) chooses the path designated for a = +1 and, with probability P(−1|Ai), the path for a = −1. However, the latter approach would be much more difficult to implement because it would require a nondemolition photon-presence detection (see, e.g., ref. 38). In the former approach, we assume that the state preparation governed by the probability distribution P(a|A) is equivalent to Alice’s nondestructive equiprobable measurements of Ai = σi for i = 1, 2, 3, where the outcomes of the measurement Ai are a = ±1 and appear with the probability P(a|Ai) = 1/2. The final measurement does not have to be nondestructive, because this is the final step of the measurement. This is sufficient to check if the channel can partially or completely erase Alice’s influence on the state detected by Bob, hence to demonstrate TS without applying a quantum nondemolition measurement.
Experimental setup for demonstrating temporal steering.
Here we use abbreviations: BS for beam splitter, PBS for polarising BS, NDF for neutral density filter of tunable transmittance τ, BDn for beam dividers, PCn for the polarisation controllers compensating polarisation rotation in the fibers, Qn for quarter-wave plates, Hn for half-wave plates, SPCM for single-photon counting module, SM for the 15 m long single-mode optical fiber which forms a delay line of t = 80 ns (this is larger than the 50 ns long dead time of the SPCM). Alice prepares the initial state by rotating a H-polarised photon with QA and HA plates. Bob performs state analysis by setting his measurement basis with HB and QB, and detecting the incoming photon in one of the orthogonal polarisation states.
A nontrivial case of TS requires a nonunitary dynamics. We implement such evolution with two channels labelled by λ. To show this evolution, we analyze the TS parameters  corresponding to the left-hand-side of the TS inequality of Chen et al.21 (see also ref. 33) and a measure of TS, i.e., the so-called TS weight wt,N, as defined in refs 33 and 39. The TS inequality is satisfied for all classical states and it reads
corresponding to the left-hand-side of the TS inequality of Chen et al.21 (see also ref. 33) and a measure of TS, i.e., the so-called TS weight wt,N, as defined in refs 33 and 39. The TS inequality is satisfied for all classical states and it reads

The technical definition of wt,N is rather complex, thus we present it in the Methods. However, this quantity measures the amount of the genuine temporal steering correlations between Alice and Bob, maximised over the possible Bob’s measurements. The TS parameter SN depends on the number N = 2, 3 of unbiased measurements Bi ≡ σi performed by Bob. This corresponds to a sum over the measurements of the expectation values  , where Bob’s outcomes are related to the state projection performed by Alice, as
, where Bob’s outcomes are related to the state projection performed by Alice, as  . The parameter N represents the number of the MUB used by Bob to analyze the received qubit. For only one channel (corresponding to a simple unitary evolution of an isolated photon), the TS parameters and the TS weight would not exhibit an interesting behaviour beyond simple oscillations. In the extreme case, when the output state of a channel is always the same, independent of the input state, Alice’s influence on the state detected by Bob is completely erased. However, for typical imperfect channels, this Alice’s influence is only partially lost and, in the context of QKD, this loss of information can be attributed to eavesdropping.
. The parameter N represents the number of the MUB used by Bob to analyze the received qubit. For only one channel (corresponding to a simple unitary evolution of an isolated photon), the TS parameters and the TS weight would not exhibit an interesting behaviour beyond simple oscillations. In the extreme case, when the output state of a channel is always the same, independent of the input state, Alice’s influence on the state detected by Bob is completely erased. However, for typical imperfect channels, this Alice’s influence is only partially lost and, in the context of QKD, this loss of information can be attributed to eavesdropping.
For both BB84 and B98 there exists a minimal value of the average quantum bit error rate (QBER) rN in the raw key for which the respective protocol is no longer secure. For individual qubit attacks these values are  for BB84 (N = 2) and
for BB84 (N = 2) and  for B98 (N = 3). These values correspond to the minimal amount of noise introduced by an eavesdropper equipped with a quantum cloning machine optimised to copy the states prepared by Alice in a relevant protocol. The security of these QKD protocols is naturally related to optimal quantum cloning and it was studied in various works (see, e.g., refs 36, 40, 41, 42, 43 and references therein). It was recently shown that the TS parameter SN depends on the average QBER rN or the average fidelity FN = 1 − rN of the states received by Bob33. This was done by expressing the steering parameter SN in terms of the fidelity Fi,a of the particular states prepared in a QKD protocol by Alice with respect to the states measured by Bob, i.e.,
for B98 (N = 3). These values correspond to the minimal amount of noise introduced by an eavesdropper equipped with a quantum cloning machine optimised to copy the states prepared by Alice in a relevant protocol. The security of these QKD protocols is naturally related to optimal quantum cloning and it was studied in various works (see, e.g., refs 36, 40, 41, 42, 43 and references therein). It was recently shown that the TS parameter SN depends on the average QBER rN or the average fidelity FN = 1 − rN of the states received by Bob33. This was done by expressing the steering parameter SN in terms of the fidelity Fi,a of the particular states prepared in a QKD protocol by Alice with respect to the states measured by Bob, i.e.,  . The derived relation between temporal steering and security of QKD33 SN > N(1 − 2rN)2 asserts that QBERN < rN. Thus, the minimal violation of this security condition indicates the maximal values of SN = N(1 − 2rN)2 for which the relevant QKD protocols are insecure.
. The derived relation between temporal steering and security of QKD33 SN > N(1 − 2rN)2 asserts that QBERN < rN. Thus, the minimal violation of this security condition indicates the maximal values of SN = N(1 − 2rN)2 for which the relevant QKD protocols are insecure.
In our experiment, λ can have two values 0 and 1. For λ = 0, a photon of polarisation V is erased, with probability p0 = 1 − τ, with a filter of transmittance τ. For λ = 1, with probability p1 = 1 − p0, the photon is passed to Bob in the state R(θ)|a|A〉. The polarisation is rotated by an angle θ, i.e., it is transformed by the operator  , where
, where  is the two-dimensional identity operator. Each time a photon is erased by the filter, Bob counts one photon received in state R(θ)|H〉. We can set the values of p0 and p1 by setting the transmission rate τ, while we set the rotation angle θ by inserting two half-wave plates into the beam (see Fig. 1). We set in the experiment τ and θ in a way that Bob receives states which can be expressed as
is the two-dimensional identity operator. Each time a photon is erased by the filter, Bob counts one photon received in state R(θ)|H〉. We can set the values of p0 and p1 by setting the transmission rate τ, while we set the rotation angle θ by inserting two half-wave plates into the beam (see Fig. 1). We set in the experiment τ and θ in a way that Bob receives states which can be expressed as

where 


 and
and  . The time tB, between Alice’s and Bob’s measurements, is measured in units of the inverse of the damping constant γ. In our experiment, we set γ = 1/t, where t = 50 ns is the time needed for a photon to make one loop in the setup. The time tB = −t log τ is set by changing the value of τ. The states in Eq. (2) correspond (up to a unitary rotation) to the solution of a simple relaxation44 model that provides an example of nonunitary dynamics.
. The time tB, between Alice’s and Bob’s measurements, is measured in units of the inverse of the damping constant γ. In our experiment, we set γ = 1/t, where t = 50 ns is the time needed for a photon to make one loop in the setup. The time tB = −t log τ is set by changing the value of τ. The states in Eq. (2) correspond (up to a unitary rotation) to the solution of a simple relaxation44 model that provides an example of nonunitary dynamics.
Finally, Bob performs polarisation analysis with a setup consisting of a set of a half- and quarter-wave plates, a polarising beam splitter (PBS), and a single-photon counting module (SPCM). This allows him to project the incoming photons on each of the |b, B〉 states. Bob receives photons arriving from both channels λ. As a result of Bob performing his projections on each of the six states |b, Bj〉, we obtain the probability distribution P(a, b|Ai, Bj) (we know what state has been sent by Alice) that holds the same information as the assemblage  . This is because
. This is because  . However, in the context of the QKD protocols we are interested only in the compatible bases (i = j), therefore,
. However, in the context of the QKD protocols we are interested only in the compatible bases (i = j), therefore,  , where δi,j is the Kronecker delta.
, where δi,j is the Kronecker delta.
Figures 2, 3 and 4 show that our experimental data are in good agreement with the expected results. However, the correspondence is not perfect due to experimental imperfections. From these measured results we calculated the TS parameters SN21,33 and the corresponding TS weights wt,N33,39. The TS inequality [see Fig. 2] provides a sufficient condition for the existence of TS and a security threshold for the MUB protocols with symmetric noise against individual attacks. In our experiment this threshold for SN is usable only for BB84 (N = 2) at a specific time tB = nπ/2, where n = 0, 1, 2. In these cases, BB84 is secure against individual attacks if the TS inequality is violated, i.e., S2 > 1. However, it is not so for B98, where the protocol can be insecure even if S3 > 1. In B98, we deal with the asymmetric dynamics of the channel (i.e., a relaxation process to one of the eigenstates of the Pauli operators); however, we can assess the security using the S3 > 4/3 condition. The increase for tBγ > 0.8 of the S2 parameter with respect to the theoretical curve, excluding the R(4tB) rotation around the y direction, is caused by interchanging the noise between the z and x directions. The TS weight, as shown in Fig. 3, which is insensitive to rotations, proves or disproves the existence of TS. Comparing Figs 2 and 3, it is clear that the relation between the TS inequality and the TS weight is not trivial. The TS weight implicitly includes all possible TS inequalities, so it detects steering better than the TS inequality. In Fig. 3, the value wt,N = 0, implies the insecurity of the relevant QKD protocol.
Evolution of the TS parameters SN corresponding to the TS inequality21,33: (a) S2 for BB84 (implemented with the eigenvalues of the Pauli operators σ1 and σ2) and (b) S3 for B98. Here, γ is the damping constant and tB is the time of the nonunitary evolution between the measurements of Alice and Bob leading to the state defined in Eq. (2). The values of S3 and S2 if the rotation R(4tB) is not implemented (noise for σ1 and σ2 measurements is uniform) are given by the dotted curves  and
and  , respectively. This also corresponds to our experiment for 4tB = 2nπ, where n = 0, 1, 2. The shrinking factor s = 0.96 takes into account the initial impurity of the states sent by Alice. The solid curves correspond to S2 and S3 calculated for the state given by Eq. (2) and accounting for the setup imperfections described in the Methods.
, respectively. This also corresponds to our experiment for 4tB = 2nπ, where n = 0, 1, 2. The shrinking factor s = 0.96 takes into account the initial impurity of the states sent by Alice. The solid curves correspond to S2 and S3 calculated for the state given by Eq. (2) and accounting for the setup imperfections described in the Methods.
Evolution of the temporal steerable weights wt,N as defined in eq: swdef.
Here, tB is the nonunitary-evolution time, γ is the damping constant, and N stands for the number of MUB, calculated for the theoretical (curves) and experimental assemblages (data points) with a semi-definite program for (a) BB84 (N = 2) and (b) B98 (N = 3). The solid curves correspond to wt,2 and wt,3 calculated for the state given by Eq. (2) and accounting for the setup imperfections described in the Methods. The temporal steerable weights do not exhibit an oscillatory behaviour because these do not depend on the choice of Bob’s measurement bases.
Evolution of the generalised Stokes parameters, i.e., the expected values of the Pauli operators Bn = σn (see ref. 33) for the six eigenstates |a, An〉 for n = 1, 2, 3 and a = ±1.
Experimental data for the relevant states with a = +1 (a = −1) are illustrated with triangles (squares). The time between Alice’s and Bob’s measurements tB is given in units of the inverse of the relaxation constant γ. In our experiment γ = 2 × 107 s−1. The solid (dashed) curves correspond to the expected values of the Pauli operators calculated for the relevant a = +1 (a = −1) states defined in Eq. (2).
Discussion
We note that a well-known technique for analysing the security in QKD is to introduce virtual entanglement by conceptually replacing state preparation with measurements on an entangled source45. Thus, one could think that the standard steering inequalities applied to the virtual entangled source can be used to determine the security requirements on the preparation and measurement correlations. Nevertheless, the described idea corresponds to analysing the security in QKD via spatial or spatio-temporal steering. In contrast with this idea, we analysed the security in QKD via purely temporal steering by replacing the two-qubit measurements with measurements on a single qubit, followed by the evolution under some noisy quantum channel.
In optical fibres one deals with several types of noise and losses which limit the range of the applicability of QKD. These problems are the polarization-dependent losses, geometric phase, birefringence, and polarization mode dispersion (see ref. 36). In our experiment, we implemented a combination of the polarization-dependent losses and polarization rotation [see Eq. (2)]. The polarization-dependent losses can be significant in components like phase modulators and open a way for attacking QKD protocols, e.g., the two-state protocol46 by changing nonorthogonal states into orthogonal ones47. However, the state-dependent losses are usually not that important in optical fibres. The polarization rotation could be attributed to the geometric phase (a special case of the Berry phase48) that accumulates, e.g., when polarised photons are transmitted through fibre loops. Alternatively, this polarization rotation can be caused by polarization-dependent dispersion due to the stress applied to optical fibres. The latter effect occurs in the polarization controllers used in our setup shown in Fig. 1.
Our analysis remains unchanged after including such additional state-independent losses like lossy quantum channels or imperfect detectors. State-dependent losses may cause some basis states to be transmitted more often than others. Thus, the security threshold should be revised by replacing the previously used rN with its optimal value found for the new asymmetric qubit distribution. This value can be calculated efficiently by optimising the the average single-copy fidelity F = 1 − rN of 1 → 2 qubit cloners49.
Conclusion
We experimentally demonstrated the possibility of temporal quantum steering with photon polarizations in a linear-optical setup. We applied TS for testing the security of two popular quantum-key distribution protocols (i.e., BB84 and B98), which are based on mutually-unbiased bases. We have measured the evolution of the TS weight33,39 and TS parameters corresponding to the violations of the TS inequalities of Chen et al.21. To our knowledge, this is the first experimental determination of the TS weight. Note that this TS weight is closely related to spatial steerable weights50,51, which have not been measured yet. Our experimental tests demonstrate the monogamy of TS and, thus, the security of the analysed cryptographic protocols against individual attacks. We believe that these first experimental demonstrations of TS can lead to useful applications in secure quantum communication.
Methods
Pauli operators in the photon-polarisation basis
We apply the standard eigenstate expansions of the Pauli operators, which read as:  ,
,  , and
, and  , where
, where  ,
,  ,
,  ,
,  ,
,  , and
, and  . These eigenstates of the Pauli operators are, respectively: the antidiagonal, diagonal, right-circular, left-circular, vertical, and horizontal polarization states.
. These eigenstates of the Pauli operators are, respectively: the antidiagonal, diagonal, right-circular, left-circular, vertical, and horizontal polarization states.
Experimental setup
Alice’s setup, as shown in Fig. 1 (in the main article) consists of QA and HA that allow her to set any of the |a, A〉 states. The polarisation modes are flipped V ↔ H by H1, then separated by BD1 and H-polarised photons are attenuated by the NDF. Next, the polarisation modes are recombined by first flipping back the polarisation modes V ↔ H by H2 and then joining the beams at BD2. The channel performs the operation R(θ) with wave plates H3 and H4. Each of these two plates implements the transformation that flips the polarisation direction along their optical axes. It can be readily shown that the two transformations constitute a rotation by angle θ = 2δ, where δ denotes the angle between the optical axes of the two wave plates. The polarisation controllers are used to stabilise the output polarisation. To satisfy the consistency conditions (see ref. 33) we assume that all the photons sent by Alice reach Bob, i.e., we interpret all the physical photon losses due to the imperfections of the photon counting process as the result of state preparation and not as the true transmission losses. However, the photons in the state R(4tB) |V〉, which are lost due to the NDF of transmittance τ, are added to the final counts, i.e., the NDF is interpreted as a part of Bob’s detection setup.
Bob’s setup consists of QB and HB followed by a PBS and SPCM (Perkin-Elmer). This setup allows to project the incoming photons onto every of the states |b, B〉. The beam splitter (BS) is used to verify if Alice has indeed prepared photons in the desired state |a, A〉 before sending them through the channel. However, the purity of states sent by Alice is p ≈ 96%, i.e., Bob’s results are effectively scaled by the shrinking factor  . Moreover, the BS rotates the photons travelling to Bob by circa 7° around the z axis with respect to the photons travelling to Alice. We take these factors into account in the presented theoretical curves, unless stated otherwise. The time delay, between the photons send via the delay loop and reflected to Bob, directly allows to analyse both the input and output states using the same detection setup. Single photons are generated using a heralded single-photon source. This source uses a type-I spontaneous parametric down-conversion (SPDC) process occurring in a 1 mm thick BBO crystal pumped by the third harmonics (355 nm) of a Nd-YAG laser (300 mW) with a repetition rate of 2500 Hz and a pulse width of 6.5 nm. The signal photon generated in the SPDC process powers the experiment, while the idler is used for triggering. We registered circa 2000 such photon pairs per second. The triggering allows us to post-select only on valid detection events (by eliminating detector dark counts) and to gate the signal detection corresponding to the direct reflection on the beam splitter BS shown in Fig. 1 of the article (no runs in the loop) from one, or possibly more runs, in the fibre loop. Our source delivers signal photons with a polarization-state purity of about 96% and a beam transversal profile corresponding to the TEM00 mode filtered by single-mode fibers. The generation rate was adjusted so that the probability of more than one photon impinging on the detector was limited to about 5%.
. Moreover, the BS rotates the photons travelling to Bob by circa 7° around the z axis with respect to the photons travelling to Alice. We take these factors into account in the presented theoretical curves, unless stated otherwise. The time delay, between the photons send via the delay loop and reflected to Bob, directly allows to analyse both the input and output states using the same detection setup. Single photons are generated using a heralded single-photon source. This source uses a type-I spontaneous parametric down-conversion (SPDC) process occurring in a 1 mm thick BBO crystal pumped by the third harmonics (355 nm) of a Nd-YAG laser (300 mW) with a repetition rate of 2500 Hz and a pulse width of 6.5 nm. The signal photon generated in the SPDC process powers the experiment, while the idler is used for triggering. We registered circa 2000 such photon pairs per second. The triggering allows us to post-select only on valid detection events (by eliminating detector dark counts) and to gate the signal detection corresponding to the direct reflection on the beam splitter BS shown in Fig. 1 of the article (no runs in the loop) from one, or possibly more runs, in the fibre loop. Our source delivers signal photons with a polarization-state purity of about 96% and a beam transversal profile corresponding to the TEM00 mode filtered by single-mode fibers. The generation rate was adjusted so that the probability of more than one photon impinging on the detector was limited to about 5%.
Experimental losses
The experimental data collected by Bob are shown in Fig. 4. The setup implements the intended transformations with an average fidelity of circa 95%. We used this value to estimate the sizes of the average error bars presented in Figs 2, 3 and 4. Moreover, the setup dephases the transmitted photons, which results in the attenuation of the off-diagonal density matrix terms by an additional factor of exp(−0.05tB). The setup introduces polarization-dependent losses, which are described by the ratio of the maximum achievable transmissivity for H-polarised photons and the maximum transmissivity for V-polarised photons (no V polarisation filtering) equal to T(H)/T(V) = 96%. Finally, there are some technological polarization-independent losses that do not affect our results, leading to a single-loop transmissivity Ttech = 10%.
Temporal steerable weight
The temporal steerable weight is a counterpart of the EPR steering weight of Skrzypczyk et al.50, where the assemblage  is formed by the set of Alice’s measurements and outcomes. The conditional probability
is formed by the set of Alice’s measurements and outcomes. The conditional probability  of Alice detecting the outcome a while setting her apparatus to measure Ai can be calculated directly from the assemblage. Bob at time tB receives states
of Alice detecting the outcome a while setting her apparatus to measure Ai can be calculated directly from the assemblage. Bob at time tB receives states  after they passed through a nonunitary channel. Thus, Bob’s assemblage is
after they passed through a nonunitary channel. Thus, Bob’s assemblage is  , where the explicit form of ρ(t) is given in the main article. To obtain this assemblage experimentally, Bob performs quantum state tomography of the received qubit.
, where the explicit form of ρ(t) is given in the main article. To obtain this assemblage experimentally, Bob performs quantum state tomography of the received qubit.
The unsteerable assemblages50 can be created independently of Alice’s observables, and can be expressed as

where γ is a random variable, ργ are the states received by Bob, and Dγ(a|Ai) are deterministic functions which assign γ to a specific measurement Ai and its outcome a33,39,50.
The TS weight wt is the minimal amount of strictly steerable resources needed to split any assemblage as

where  is a steerable assemblage and
is a steerable assemblage and  is an unsteerable assemblage. The smallest possible value of 0 ≤ wt ≤ 1 in Eq. (4) corresponds to the TS weight. Thus, to find its value one needs to solve a convex optimization problem. For small matrices, this can be done efficiently using semi-definite programming.
is an unsteerable assemblage. The smallest possible value of 0 ≤ wt ≤ 1 in Eq. (4) corresponds to the TS weight. Thus, to find its value one needs to solve a convex optimization problem. For small matrices, this can be done efficiently using semi-definite programming.
Additional Information
How to cite this article: Bartkiewicz, K. et al. Experimental temporal quantum steering. Sci. Rep. 6, 38076; doi: 10.1038/srep38076 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Schrödinger, E. Discussion of probability relations between separated systems. Math. Proc. Camb. Phil. Soc. 31, 555–563 (1935).
Einstein, A., Podolsky, B. & Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935).
Cavalcanti, E. G., Broadbent, C. J., Walborn, S. P. & Wiseman, H. M. 80 years of steering and the Einstein–Podolsky–Rosen paradox: introduction. J. Opt. Soc. B 32, EPR1 (2015).
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865–942 (2009).
Bell, J. S. Steering, entanglement, nonlocality, and the Einstein-Podolsky-Rosen paradox. Physics 1, 195–200 (1964).
Genovese, M. Research on hidden variable theories: A review of recent progresses. Physics Reports 413, 319–396 (2005).
Brunner, N., Cavalcanti, D., Pironio, S., Scarani, V. & Wehner, S. Bell nonlocality. Rev. Mod. Phys. 86, 419–478 (2014).
Wiseman, H. M., Jones, S. J. & Doherty, A. C. Steering, entanglement, nonlocality, and the Einstein-Podolsky-Rosen paradox. Phys. Rev. Lett. 98, 140402 (2007).
Cavalcanti, E. G., Jones, S. J., Wiseman, H. M. & Reid, M. D. Experimental criteria for steering and the Einstein-Podolsky-Rosen paradox. Phys. Rev. A 80, 032112 (2009).
Smith, D. H. et al. Conclusive quantum steering with superconducting transition-edge sensors. Nat. Commun. 3, 625 (2012).
Saunders, D. J., Jones, S. J., Wiseman, H. M. & Pryde, G. J. Experimental EPR-steering using Bell-local states. Nat. Phys. 6, 845–849 (2010).
Walborn, S. P., Salles, A., Gomes, R. M., Toscano, F. & Souto Ribeiro, P. H. Revealing hidden Einstein-Podolsky-Rosen nonlocality. Phys. Rev. Lett. 106, 130402 (2011).
Bennet, A. J. et al. Arbitrarily loss-tolerant Einstein-Podolsky-Rosen steering allowing a demonstration over 1 km of optical fiber with no detection loophole. Phys. Rev. X 2, 031003 (2012).
Händchen, V. et al. Observation of one-way Einstein-Podolsky-Rosen steering. Nat. Photon. 6, 596–599 (2012).
Steinlechner, S., Bauchrowitz, J., Eberle, T. & Schnabel, R. Strong Einstein-Podolsky-Rosen steering with unconditional entangled states. Phys. Rev. A 87, 022104 (2013).
Su, H. Y., Chen, J. L., Wu, C., Deng, D. L. & Oh, C. H. Detecting Einstein-Podolsky-Rosen steering for continuous variable wavefunctions. I. J. Quant. Infor. 11, 1350019 (2013).
Schneeloch, J., Dixon, P. B., Howland, G. A., Broadbent, C. J. & Howell, J. C. Violation of continuous-variable Einstein-Podolsky-Rosen steering with discrete measurements. Phys. Rev. Lett. 110, 130407 (2013).
Wittmann, B. et al. Loophole-free Einstein-Podolsky-Rosen experiment via quantum steering. New J. Phys. 14, 053030 (2012).
Branciard, C., Cavalcanti, E. G., Walborn, S. P., Scarani, V. & Wiseman, H. M. One-sided device-independent quantum key distribution: Security, feasibility, and the connection with steering. Phys. Rev. A 85, 010301 (2012).
Acin, A. et al. Device-independent security of quantum cryptography against collective attacks. Phys. Rev. Lett. 98, 230501 (2007).
Chen, Y.-N. et al. Temporal steering inequality. Phys. Rev. A 89, 032112 (2014).
Ou, Z. Y., Pereira, S. F., Kimble, H. J. & Peng, K. C. Realization of the Einstein-Podolsky-Rosen paradox for continuous variables. Phys. Rev. Lett. 68, 3663–3666 (1992).
Hald, J., Sørensen, J. L., Schori, C. & Polzik, E. S. Spin squeezed atoms: A macroscopic entangled ensemble created by light. Phys. Rev. Lett. 83, 1319–1322 (1999).
Bowen, W. P., Schnabel, R., Lam, P. K. & Ralph, T. C. Experimental investigation of criteria for continuous variable entanglement. Phys. Rev. Lett. 90, 043601 (2003).
Howell, J. C., Bennink, R. S., Bentley, S. J. & Boyd, R. W. Realization of the Einstein-Podolsky-Rosen paradox using momentum- and position-entangled photons from spontaneous parametric down conversion. Phys. Rev. Lett. 92, 210403 (2004).
Chen, J.-L. et al. All-Versus-Nothing Proof of Einstein-Podolsky-Rosen Steering. Sci. Rep. 3 (2013).
Sun, K. et al. Experimental demonstration of the Einstein-Podolsky-Rosen steering game based on the all-versus-nothing proof. Phys. Rev. Lett. 113, 140402 (2014).
Chen, J.-L. et al. Beyond Gisin’s Theorem and its Applications: Violation of Local Realism by Two-Party Einstein-Podolsky-Rosen Steering. Sci. Rep. 5, 11624 (2015).
Wollmann, S., Walk, N., Bennet, A. J., Wiseman, H. M. & Pryde, G. J. Observation of Genuine One-Way Einstein-Podolsky-Rosen Steering. Phys. Rev. Lett. 116, 160403 (2016).
Sun, K. et al. Experimental Quantification of Asymmetric Einstein-Podolsky-Rosen Steering. Phys. Rev. Lett. 116, 160404 (2016).
Bennett, C. H. & Brassard, G. Public key distribution and coin tossing. In Proc. IEEE Int. Conf. on Computers, Systems and Signal Processing175, 8 (1984).
Bruß, D. Optimal eavesdropping in quantum cryptography with six states. Phys. Rev. Lett. 81, 3018–3021 (1998).
Bartkiewicz, K., Černoch, A., Lemr, K., Miranowicz, A. & Nori, F. Temporal steering and security of quantum key distribution with mutually unbiased bases against individual attacks. Phys. Rev. A 93, 062345 (2016).
Shor, P. W. & Preskill, J. Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 85, 441–444 (2000).
Lo, H.-K. Proof of unconditional security of six-state quatum key distribution scheme. Quantum Information and Computation 1, 81–94 (2001).
Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002).
Gerlach, W. & Stern, O. Das magnetische moment des silberatoms. Z. Phys. 9, 353–355 (1922).
Bula, M., Bartkiewicz, K., Černoch, A. & Lemr, K. Entanglement-assisted scheme for nondemolition detection of the presence of a single photon. Phys. Rev. A 87, 033826 (2013).
Chen, S. L. et al. Quantifying Non-Markovianity with Temporal Steering. Phys. Rev. Lett. 116, 020503 (2016).
Soubusta, J., Bartůšková, L., Černoch, A., Fiurášek, J. & Dušek, M. Several experimental realizations of symmetric phase-covariant quantum cloners of single-photon qubits. Phys. Rev. A 76, 042318 (2007).
Bartůšková, L., Dušek, M., Černoch, A., Soubusta, J. & Fiurášek, J. Fiber-optics implementation of an asymmetric phase-covariant quantum cloner. Phys. Rev. Lett. 99, 120505 (2007).
Lemr, K., Bartkiewicz, K., Černoch, A., Soubusta, J. & Miranowicz, A. Experimental linear-optical implementation of a multifunctional optimal qubit cloner. Phys. Rev. A 85, 050307 (2012).
Bartkiewicz, K., Lemr, K., Černoch, A., Soubusta, J. & Miranowicz, A. Experimental eavesdropping based on optimal quantum cloning. Phys. Rev. Lett. 110, 173601 (2013).
Zagoskin, A. M. Quantum Engineering: Theory and Design of Quantum Coherent Structures (Cambridge University Press, 2011).
Nielsen, M. A. & Chuang, I. L. Quantum computation and quantum information (Cambridge University Press, 2010).
Bennett, C. H. Quantum cryptography using any two nonorthogonal states. Phys. Rev. Lett. 68, 3121–3124 (1992).
Huttner, B., Muller, A., Gautier, J. D., Zbinden, H. & Gisin, N. Unambiguous quantum measurement of nonorthogonal states. Phys. Rev. A 54, 3783–3789 (1996).
Berry, M. V. Quantal phase factors accompanying adiabatic changes. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 392, 45–57 (1984).
Bartkiewicz, K., Černoch, A., Chimczak, G., Miranowicz, A. & Nori, F. Experimental quantum forgery of quantum optical money. arXiv:1604.04453v1 (2016).
Skrzypczyk, P., Navascués, M. & Cavalcanti, D. Quantifying Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 112, 180404 (2014).
Piani, M. & Watrous, J. Necessary and sufficient quantum information characterization of Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 114, 060404 (2015).
Acknowledgements
K.L. and K.B. acknowledge the financial support by the Czech Science Foundation under the project No. 16-10042Y and the financial support of the Polish National Science Centre under grant DEC-2013/11/D/ST2/02638. A.Č. acknowledges financial support by the Czech Science Foundation under the project No. P205/12/0382. The authors also acknowledge the project No. LO1305 of the Ministry of Education, Youth and Sports of the Czech Republic financing the infrastructure of their workplace. F.N. is partially supported by the RIKEN iTHES Project, MURI Center for Dynamic Magneto-Optics, JSPS-RFBR contract no. 12-02-92100, JST-IMPACT, CREST, and a Grant-in-Aid for Scientific Research (A). A.M. and F.N. acknowledge the support of a grant from the John Templeton Foundation.
Author information
Authors and Affiliations
Contributions
K.B. and A.M. developed the theoretical framework. K.B. planned the experiment, processed the experimental data, and wrote the paper. A.Č. and K.L. designed and built the experimental setup and performed the measurements. All authors discussed the results and participated in the manuscript preparation.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Bartkiewicz, K., Černoch, A., Lemr, K. et al. Experimental temporal quantum steering. Sci Rep 6, 38076 (2016). https://doi.org/10.1038/srep38076
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep38076
This article is cited by
-
Does conditional entropy squeezing indicate normalized entropic uncertainty relation steering?
Quantum Information Processing (2024)
-
Sudden death and revival of Gaussian Einstein–Podolsky–Rosen steering in noisy channels
npj Quantum Information (2021)
-
Partial Steerability and Nonlocality of Multipartite Quantum States
International Journal of Theoretical Physics (2021)
-
Experimental test of non-macrorealistic cat states in the cloud
npj Quantum Information (2020)
-
Bell-type inequalities of \(l_1\)-norm of coherence
Quantum Information Processing (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.