Abstract
The generation and quantification of quantum entanglement is crucial for quantum information processing. Here we study the transition of Gaussian correlation under the effect of linear optical beam-splitters. We find the single-mode Gaussian coherence acts as the resource in generating Gaussian entanglement for two squeezed states as the input states. With the help of consecutive beam-splitters, single-mode coherence and quantum entanglement can be converted to each other. Our results reveal that by using finite number of beam-splitters, it is possible to extract all the entanglement from the single-mode coherence even if the entanglement is wiped out before each beam-splitter.
Similar content being viewed by others
Introduction
Quantum correlation, especially quantum entanglement, is a key ingredient in quantum information science. Since the Einstein-Podolsky-Rosen (EPR) paradox has been put forward1, quantum correlation has been investigated both in theory and in experiments2,3,4,5,6,7,8. During the past decades, the characterization and definition of quantum correlation have attracted much research interest, such as Bell non-locality, quantum steering, quantum entanglement, quantum discord, and quantum coherence9,10,11,12,13,14,15,16,17. It has been pointed out that these definitions satisfy hierarchy relations, i.e., quantum coherence > quantum discord > quantum entanglement > quantum steering > Bell non-locality18,19,20,21, where A > B represents B is a subset of A, meaning all steerable states are entangled, but not all entangled states have steering, etc. On the other hand, quantum entanglement characterizes the nonclassical property of multipartite quantum systems. An entangled state can not be decomposed as a convex sum of product states14, if two subsystems are entangled, the quantum state of each subsystem can not be described independently. Quantum entanglement only represents the nonclassical property between the subsystems which can not characterize the nonclassical property of a single-party system. Non-classicality can be used to characterize its nonclassical property of the quantum states, such as squeezed states, anti-bunched states, and sub-Poissonian states22. The non-classicality characterizes the quantumness of a single-party quantum system. The concept of quantum steering comes from the EPR paradox. For a quantum system consisting of subsystems marked with A and B, A can steer B if A can affect B’s subsystem by using a local operation on A’s subsystem. Quantum steering has many useful applications, such as sub-channel discrimination, one-side device-independent quantum key distribution, etc23,24,25,26.
In addition to quantum correlation, quantum coherence can also be used to characterize the nonclassical property of both multipartite and single-party quantum systems. Quantum coherence is one of the key features of quantum mechanics, several experiments have revealed that quantum coherence exists in photosynthetic complexes and indicating that it plays a key role in high efficiency achievements in photosynthesis27,28. Quantum coherence can be quantified by the off-diagonal elements in the density matrix of the system under the reference basis, which is called the l1 norm coherence. Another way to measure coherence is the relative entropy coherence defined as the entropy difference between the density matrix of the quantum state and the diagonal density matrix that eliminating all the off-diagonal elements of the original density matrix.
Quantum systems can be roughly partitioned into discrete and continuous variable ones. As the most important family of continuous quantum states, Gaussian states are widely used because of its availability and controllability in experiments29. Recently, some representative applications have been investigated, such as quantum communication, ultrasensitive sensing, detection and imaging, and so on ref. 30. Different from discrete variable quantum states13,14,15, the approaches of quantifying the quantum correlation of continuous variable quantum states are more complicated12,31,32. Here in this study, we will give a detailed mathematical expression of Gaussian correlation and investigate the Gaussian correlation generated by beam-splitters in experiments. Beam-splitters are key components in optics, and have been used in many experiments including Bell test experiment, Wheeler’s delayed choice experiment, etc33,34. Especially in quantum information processing, Knill et al. pointed that efficient quantum computation is possible to be realized by using only beam-splitters, phase shifters, single photon sources and photo-detectors35. Although beam-splitters are linear optical devices, they can generate quantum entanglement36,37,38,39.
In this work, we study the behavior of the quantum correlation of Gaussian states under the effect of beam-splitters. We find that the non-classicality of single-mode Gaussian state generates entanglement by beam-splitters40 is not valid for all single-mode Gaussian states. Instead, single-mode coherence plays a vital role in such process. By using consecutive beam-splitters, we find the single-mode coherence and quantum entanglement could be converted to each other for two squeezed states as the input states. Moreover, if we further wipe out the entanglement before each beam-splitter, all the quantum entanglement can be extracted from the single-mode coherence by a finite number of beam-splitters.
Results
Entanglement and steering generation using single beam-splitter
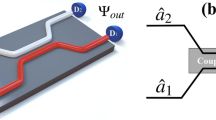
Here we consider two single-mode Gaussian optical beams send into the two input ports of one beam-splitter. The covariance matrix of the output Gaussian optical beam can be characterized by

where σout(in) is the covariance matrix of the output (input) optical beam, U(θ, ϕ) could be described by40

where  denotes the transmittance and ϕ represents the phase difference between the reflected and transmitted fields. Here we consider the case where two single-mode input Gaussian optical beams are squeezed lights, one (say mode A) is squeezed in position quadrature and the other one (say mode B) is squeezed in momentum quadrature. The covariance matrices of modes A and B are given by
denotes the transmittance and ϕ represents the phase difference between the reflected and transmitted fields. Here we consider the case where two single-mode input Gaussian optical beams are squeezed lights, one (say mode A) is squeezed in position quadrature and the other one (say mode B) is squeezed in momentum quadrature. The covariance matrices of modes A and B are given by

where rA(B) is the squeezing parameter for mode A (B). The covariance matrix of the output optical beam becomes σout = U†(θ, ϕ) (σA⊕σB)U (θ, ϕ).
The quantum steering of the output optical beams could be calculated by

where  . It is obvious that quantum steering can be created by the beam-splitter except the case where rA = −rB (meaning two optical beams are identical) or θ = nπ/2 (n is an integer). By considering the case
. It is obvious that quantum steering can be created by the beam-splitter except the case where rA = −rB (meaning two optical beams are identical) or θ = nπ/2 (n is an integer). By considering the case  , the maximal value of quantum steering is found at the point θ = (2n + 1)π/4. And the quantum entanglement of the output state could be obtained by
, the maximal value of quantum steering is found at the point θ = (2n + 1)π/4. And the quantum entanglement of the output state could be obtained by

where  .
.
In the following, we will study the change of the non-classicality of the two single-mode Gaussian states after the action of a beam-splitter. By using

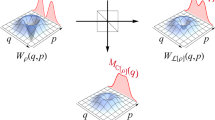
one can find NΔ exhibits the similar behavior as quantum entanglement. In a previous work40, the authors have found that the non-classicality creates entanglement in the case where the input states are nonclassical Gaussian states and vacuum states. Here we do not use these states as the input states because mixing these two states by a beams splitter can not generate quantum steering. However, when the two input single-mode Gaussian states are two squeezed lights, their finding is not valid since NΔ ≥ 0 does not always satisfied. Here Fig. 1(a) describes the region where NΔ < 0 (rA = rB = r), and Fig. 1(b) displays the transition of quantum correlation when we regard θ as an independent variable and assume that rA = rB = 0.2. One may find that when 0 < θ < 0.33 and  , both quantum steering and quantum entanglement increase and the non-classicality also increase. Therefore, quantum entanglement and quantum steering are not generated by single-mode non-classicality.
, both quantum steering and quantum entanglement increase and the non-classicality also increase. Therefore, quantum entanglement and quantum steering are not generated by single-mode non-classicality.
The quantum correlation of the Gaussian optical beams undergoing a beam-splitter, where the input states are two squeezed lights.
(a) Represents the difference of the single-mode non-classicality between input Nin and output Nout optical beams where rA = rB = r. (b) Represents the change of the quantum correlation when rA = rB = 0.2, where CΔ is the difference of the single-mode coherence between input and output optical beams, EN is the quantum entanglement of the output beam, TA→B is the quantum steering of the output beam.
Then we consider single-mode coherence as

we find the relation CΔ ≥ 0, and CΔ equals to zero only when rA = −rB or θ = nπ/2. Meanwhile, CΔ shows similar behavior as quantum entanglement and quantum steering. Here we numerically study the change of single-mode coherence in Fig. 1(b), where we choose θ as an independent variable and rA = rB = 0.2. Since Cin keeps as a constant with a fixed θ, when Cout = C(A)out + C(B)out decreases, both quantum entanglement and quantum steering increase, meaning that they can be generated by single-mode coherence. Here we can conclude that quantum entanglement between two-mode Gaussian states can be regarded as an intrinsic coherence, i.e., coherence between the two modes. The intrinsic coherence and single-mode coherence are complementary to each other. In other words, intrinsic coherence increases along with the decrement of single-mode coherence41. According to the definition42, quantum correlations originates from the superposition of quantum states. The single-mode coherence can characterize the superposition of the subsystem (the local superposition), the intrinsic coherence (or quantum entanglement) represents the superposition between the subsystems (the unlocal superposition). Our observation indicates that the beam-splitters can be used to convert local superposition to nonlocal superposition, and vice versa.
Conversion between entanglement and quantum steering using Gaussian optical beams
We study in the following the case when more than one beam-splitters are used to mix the squeezed lights. From Eq. (2), we find that U(θ, ϕ) is a periodic function by considering θ as an independent variable. By choosing the input optical beams at the beam-splitters with  (see Fig. 2(a)), we find both quantum entanglement and quantum steering increase after the first and second beam-splitters, and decrease when undergoing the third and fourth ones while quantum coherence shows the opposite behavior. Here in Fig. 3(a,b,c), we plot the evolution of quantum steering, quantum entanglement and quantum coherence for different number of beam-splitters as n = 1, 2, 3, 4, respectively. It is obvious that under the effect of consecutive beam-splitters, quantum entanglement (quantum steering) and quantum coherence convert to each other. Figure 3(d) illustrates the evolution of quantum correlation when θ = π/128 and rA = rB = 0.2. In this case, the evolution of the quantum correlation behaves like a non-Markov process without loss. Therefore, with the memory effect, consecutive beam-splitters can be used to simulate the non-Markovian environment.
(see Fig. 2(a)), we find both quantum entanglement and quantum steering increase after the first and second beam-splitters, and decrease when undergoing the third and fourth ones while quantum coherence shows the opposite behavior. Here in Fig. 3(a,b,c), we plot the evolution of quantum steering, quantum entanglement and quantum coherence for different number of beam-splitters as n = 1, 2, 3, 4, respectively. It is obvious that under the effect of consecutive beam-splitters, quantum entanglement (quantum steering) and quantum coherence convert to each other. Figure 3(d) illustrates the evolution of quantum correlation when θ = π/128 and rA = rB = 0.2. In this case, the evolution of the quantum correlation behaves like a non-Markov process without loss. Therefore, with the memory effect, consecutive beam-splitters can be used to simulate the non-Markovian environment.
To obtain the condition under which quantum entanglement is wiped out before the input optical beams and further mixed by the next beam-splitter, as illustrated by Fig. 2(b), we find that the quantum entanglement of the input beams after the last beam-splitter will decrease with the increment of the number of the beam-splitters. And the number of beam-splitters depends on θ, for instance, when  , quantum entanglement can only be generated by the first beam-splitter. When θ → 0, quantum entanglement can always be generated. Figure 4 shows the quantum entanglement, quantum steering and single-mode coherence when considering n = 1, 2, 3, 4. The quantity of the generated entanglement depends on single-mode coherence of the input states. Once quantum entanglement has been erased, it can not convert back into single-mode coherence, and the observed entanglement will decrease with respect to n. On the other hand, quantum steering can only be generated by the first beam-splitter regardless of θ (see Fig. 4(b)). Since quantum entanglement has been wiped out before the consecutive beam-splitters, we can conclude that the process could be observed during which quantum entanglement is converted to quantum steering.
, quantum entanglement can only be generated by the first beam-splitter. When θ → 0, quantum entanglement can always be generated. Figure 4 shows the quantum entanglement, quantum steering and single-mode coherence when considering n = 1, 2, 3, 4. The quantity of the generated entanglement depends on single-mode coherence of the input states. Once quantum entanglement has been erased, it can not convert back into single-mode coherence, and the observed entanglement will decrease with respect to n. On the other hand, quantum steering can only be generated by the first beam-splitter regardless of θ (see Fig. 4(b)). Since quantum entanglement has been wiped out before the consecutive beam-splitters, we can conclude that the process could be observed during which quantum entanglement is converted to quantum steering.
Summary
We have studied the progress of quantum entanglement and quantum steering generation using beam-splitters. We have found that instead of the single-mode Gaussian non-classicality, single-mode Gaussian coherence acts as the fundamental resource for generating two-mode Gaussian entanglement and steering for two squeezed states as the input states. The covariance matrix of general one-mode Gaussian states can be written as  where VS is the covariance matrix of squeezed states,
where VS is the covariance matrix of squeezed states,  is a constant, R represents the phase rotation operator. By further calculations, we find when the two input squeezed states have the same phase rotation, the conclusion is also correct. Therefore, we suppose the conclusion is valid for general one-mode Gaussian states. Based on the former results, it has been confirmed by the observation that single-mode coherence and the entanglement are complementary to each other, namely, quantum entanglement increases while single-mode coherence decreases, and vice versa.
is a constant, R represents the phase rotation operator. By further calculations, we find when the two input squeezed states have the same phase rotation, the conclusion is also correct. Therefore, we suppose the conclusion is valid for general one-mode Gaussian states. Based on the former results, it has been confirmed by the observation that single-mode coherence and the entanglement are complementary to each other, namely, quantum entanglement increases while single-mode coherence decreases, and vice versa.
Meanwhile, we have discussed the evolution of quantum entanglement under the action by several beam-splitters on two single squeezed states, and discovered that quantum entanglement and single-mode coherence transfers to each other periodically. If we wipe out the entanglement in the consecutive beam-splitters, only the first beam-splitter generates quantum steering. We hope these results on quantum correlation could further develop the applications in quantum information processing.
Method
Definition of Gaussian states
The continuous variable quantum system (Gaussian state) is always difficult to be characterized by using the density matrix since the dimensionality of the density matrix is infinite. Here we consider the canonical operators in the vector by  , where
, where  , and
, and  (
( ) are the creation (annihilation) operators for the n-bosonic mode system. The elements in
) are the creation (annihilation) operators for the n-bosonic mode system. The elements in  satisfy the commutation relation as
satisfy the commutation relation as  where
where  is denoted the symplectic form.
is denoted the symplectic form.
The covariance matrix σ contains the elements of which is defined by29

Here the diagonal elements of σ are the variance of  and the off-diagonal elements encode the inter-modal correlations among subsystems. And the quantity
and the off-diagonal elements encode the inter-modal correlations among subsystems. And the quantity  is defined as the mean value of
is defined as the mean value of  . The physical meanings of
. The physical meanings of  characterizes the center of the probability distribution in phase space and σ describes its shape.
characterizes the center of the probability distribution in phase space and σ describes its shape.
The covariance matrix of a two-mode Gaussian state consisting of parties A and B could be expressed as

where  and
and  are the covariance matrices for subsystems A and B. And
are the covariance matrices for subsystems A and B. And  characterizes the correlation between A and B.
characterizes the correlation between A and B.
Quantum correlation of Gaussian states
The definition of negativity characterizes by the entanglement of two-partite discrete variable systems14,15. Similar to discrete variable condition, we use logarithmic negativity to characterize the entanglement of Gaussian states, which can be calculated by E = max{0, −log2v}, where v is the smallest symplectic eigenvalue of the partial transpose of the covariance matrix. This definition also originates from the positive partial transpose (PPT) criteria15,31. In this work, we consider two-mode Gaussian states, the partial transpose is defined as

where R = diag{1, −1, 1, 1}, and σAB denotes the covariance matrix of the two-mode Gaussian state.
Quantum steering is also a type of quantum correlation whose definition is located between quantum entanglement and Bell non-locality12. It describes how local operations on one subsystem effects another. Assuming that a two-mode Gaussian state consisting of subsystems A and B, A can steer B by A’s Gaussian measurements if the condition σAB + i(0A ⊕ ΩB) ≥ 0 is violated43, where Gaussian measurements consists a measurement set that maps Gaussian states into Gaussian ones. The quantum steering from A to B can be obtained by

The definition above is only suitable for two-mode Gaussian states, consisting of subsystems A and B, by implementing Gaussian measurements on A’s subsystem. In this paper, we use Eq. (11) to calculate the quantum steering of two-mode Gaussian states.
The non-classicality represents the nonclassical property of the non-classical states, such as squeezed states, anti-bunched states, and sub-Poissonian states whose correlation function can not be reproduced by any classical field22. The non-classicality of the Gaussian states can be characterized by the covariance matrix of the system. For single-mode Gaussian states, some quantities (for example, the degree of squeezing) are used to characterize the non-classicality. In this paper, we use N = −log2λmin to calculate the non-classicality40, where λmin is the minimum eigenvalue of the covariance matrix (ref. 40 gives the equation N = −log22λmin since they defined  .
.
Quantum coherence characterizes the superposition property of quantum systems. The relative entropy coherence for discrete variable systems can be written as ref. 13

where S(ρ) = −Tr(ρlog2ρ), and ρdiag denotes the diagonal density matrix that eliminating all the off-diagonal elements of ρ under the reference basis. In this paper, we use the coherence measure as  , where δ is the nearest incoherent Gaussian state of ρ. The coherence of one-mode Gaussian states is ref. 32:
, where δ is the nearest incoherent Gaussian state of ρ. The coherence of one-mode Gaussian states is ref. 32:

where  and
and  denotes the mean value of the thermal state number, which can be calculated by
denotes the mean value of the thermal state number, which can be calculated by  , where xi(i = 1, 2) are the components of
, where xi(i = 1, 2) are the components of  . In this study, we choose xi = 0 and we have
. In this study, we choose xi = 0 and we have  .
.
Additional Information
How to cite this article: Wang, Z.-X. et al. Gaussian entanglement generation from coherence using beam-splitters. Sci. Rep. 6, 38002; doi: 10.1038/srep38002 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Einstein, A., Podolsky, B. & Rosen, N. Can quantum-mechanical description of physical reality be considered complete. Phys. Rev. 47, 777 (1935)
Aguilar, G. H. et al. Experimental estimate of a classicality witness via a single measurement. Phys. Rev. Lett. 108, 063601 (2012).
Silva, I. A. et al. Measuring bipartite quantum correlations of an unknown state. Phys. Rev. Lett. 110, 140501 (2013).
Luo, S. Quantum discord for two-qubit systems. Phys. Rev. A 77, 042303 (2008).
Li B., Wang, Z. H. & Fei, S. M. Quantum discord and geometry for a class of two-qubit states. Phys. Rev. A 83, 022321 (2011).
Ali, M., Rau, A. R. P. & Alber, G. Quantum discord for two-qubit X states. Phys. Rev. A 81, 042105 (2010).
Adesso, G. & Datta, A. Quantum versus classical correlations in gaussian states. Phys. Rev. Lett. 105, 030501 (2010).
Giorda, P. & Paris, M. G. A. Gaussian quantum discord. Phys. Rev. Lett. 105, 020503 (2010).
Modi, K., Brodutch, A., Cable, H., Paterek, T. & Vedral, V. The classical-quantum boundary for correlations: Discord and related measures. Rev. Mod. Phys. 84, 1655 (2012).
Ollivier, H. & Zurek, W. H. Quantum discord: A measure of the quantumness of correlations. Phys. Rev. Lett. 88, 017901 (2001).
Skrzypczyk, P., Navascues, M. & Canalcanti, D. Quantifying Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 112, 180404 (2014).
Kogias, I., Lee, A. R., Ragy, S. & Adesso, G. Quantification of gaussian quantum steering. Phys. Rev. Lett. 114, 060403 (2015).
Baumgratz, T., Cramer M. & Plenio, M. B. Quantifying coherence. Phys. Rev. Lett. 113, 140401 (2015).
Bennett, C. H., Divincenzo, D. P., Smolin, J. A. & Wootters, W. K. Mixed-state entanglement and quantum error correction. Phys. Rev. A 54, 3824 (1996).
Vidal, G. & Werner, R. F. Computable measure of entanglement. Phys. Rev. A 65, 032314 (2002).
Zhou, L. & Sheng, Y. B. Detection of nonlocal atomic entanglement assisted by single photons. Phys. Rev. A 90, 024301 (2014).
Sheng, Y. B., Guo, R., Pan, J., Zhou, L. & Wang, X. F. Two-step measurement of the concurrence for hyperentangled state. Quant. Inf. Process. 14, 963–978(2015).
Adesso, G., Bromley, T. R. & Cianciaruso, M. Measures and applications of quantum correlations. arXiv:quant-ph 1605.00806v1 (2016).
Brunner, N., Cavalcanti, D., Pironio S., Scarani, V. & Wehner, S. Bell nonlocality. Rev. Mod. Phys. 86, 419 (2014).
Piani, M. & Watrous, J. Necessary and sufficient quantum information characterization of Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 114, 060404 (2015).
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009).
Marian, P., Marian, T. A. & Scutaru, H. Quantifying nonclassicality of one-mode gaussian states of the radiation field. Phys. Rev. Lett. 88, 153601 (2002).
Piani, M. & Watrous, J. Einstein-Podolsky-Rosen steering provides the advantage in entanglement-assisted subchannel discrimination with one-way measurements. arXiv:1406.0530 (2014).
Branciard, C., Cavalcanti, E. G., Walborn, S. P., Scarani, V. & Wiseman, H. M. One-sided device-independent quantum key distribution: Security, feasibility, and the connection with steering. Phys. Rev. A 85, 010301 (2012).
Bartkiewicz, K., Cernoch, A., Lemr, K., Miranowicz, A. & Nori, F. Temporal steering and security of quantum key distribution with mutually-unbiased bases against individual attacks. arXiv:1503.00612 (2015).
Wittmann, B. et al. Loophole-free EinsteinšCPodolskyšCRosen experiment via quantum steering. New J. Phys 14, 053030 (2012).
Engel, G. S. et al. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 446, 782 (2007).
Calhoun, T. R. & Fleming, G. R. Quantum coherence in photosynthetic complexes. Phys. Status. Solidi B 248. No. 4, 833 (2011).
Braunstein, S. L. & van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 77, 513 (2005).
Weedbrook, C. et al. Gaussian quantum information. Rev. Mod. Phys. 84, 621 (2012).
Adesso, G. Entanglement of Gaussian states. arXiv:quant-ph/0702069 (2007).
Xu, J. Quantifying coherence of gaussian states. Phys. Rev. A 93, 032111 (2016).
Freedman, S. J. & Clauser, J. F. Experimental test of local hidden-variable theories. Phys. Rev. Lett. 28, 938 (1972).
Marlow, A. R. Mathematical Foundations of Quantum Theory. Academic Press, P39 (1978).
Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).
Wolf, M. M., Eisert, J. & Plenio, M. B. Entangling power of passive optical elements. Phys. Rev. Lett. 90, 047904 (2003).
Asboth, J. K., Calsamiglia, J. & Ritsch, H. Computable measure of nonclassicality for light. Phys. Rev. Lett. 94, 173602 (2005).
Jiang, Z., Lang, M. D. & Caves, C. M. Mixing nonclassical pure states in a linear-optical network almost always generates modal entanglement. Phys. Rev. A 88, 044301 (2013).
Gholipour, H. & Shahandeh, F. Entanglement and nonclassicality: A mutual impression. Phys. Rev. A 93, 062318 (2016).
Ge, W., Tasgin, M. E. & Zubairy, M. S. Conservation relation of nonclassicality and entanglement for gaussian states in a beam splitter. Phys. Rev. A 92, 052328 (2015).
Radhakrishnan, C., Parthasarathy, M., Jambulingam, S. & Byrnes, T. Distribution of quantum coherence in multipartite system. Phys. Rev. Lett. 116, 150504 (2016).
Dirac, P. A. M. The Principles of Quantum Mechanics (4th Edition). Oxford University Press (1958).
Wiseman, H. M., Jones, S. J. & Doherty, A. C. Steering, entanglement, nonlocality, and the Einstein-Podolsky-Rosen paradox. Phys. Rev. Lett. 98, 140402 (2007).
Acknowledgements
The authors gratefully acknowledge the support from the National Natural Science Foundation of China through Grants Nos. 61622103, 61471050 and 11404031, the Fok Ying-Tong Education Foundation for Young Teachers in the Higher Education Institutions of China (Grant No. 151063), the Open Research Fund Program of the State Key Laboratory of Low-Dimensional Quantum Physics, Tsinghua University Grant No. KF201610.
Author information
Authors and Affiliations
Contributions
Z.W., S.W. and C.W. wrote the main manuscript text, Z.W. and S.W. prepared figures 1–5. All the authors reviewed the manuscript and discussed the results, drew conclusions and edited the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Wang, ZX., Wang, S., Ma, T. et al. Gaussian entanglement generation from coherence using beam-splitters. Sci Rep 6, 38002 (2016). https://doi.org/10.1038/srep38002
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep38002
This article is cited by
-
Hierarchy of quantum correlations using a linear beam splitter
Scientific Reports (2018)
-
Quantum coherence of the Heisenberg spin models with Dzyaloshinsky-Moriya interactions
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.





 . (d) Represents the case where
. (d) Represents the case where  . The subscripts represent the number of beam-splitters.
. The subscripts represent the number of beam-splitters.