Abstract
Charge density wave (CDW) formation, a key physics issue for materials, arises from interactions among electrons and phonons that can also lead to superconductivity and other competing or entangled phases. The prototypical system TiSe2, with a particularly simple (2 × 2 × 2) transition and no Kohn anomalies caused by electron-phonon coupling, is a fascinating but unsolved case after decades of research. Our angle-resolved photoemission measurements of the band structure as a function of temperature, aided by first-principles calculations, reveal a hitherto undetected but crucial feature: a (2 × 2) electronic order in each layer sets in at ~232 K before the widely recognized three-dimensional structural order at ~205 K. The dimensional crossover, likely a generic feature of such layered materials, involves renormalization of different band gaps in two stages.
Similar content being viewed by others
Introduction
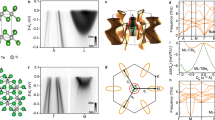
The rich physics of CDW is exemplified by the varied properties of a large number of transition-metal dichalcogenides1,2,3,4,5,6,7,8,9,10, which are additionally of interest for their potential as alternates of graphene/graphite for electronic applications. TiSe2 is an especially simple case. Its crystal structure (Fig. 1A) consists of Se-Ti-Se trilayers loosely bonded together by van der Waals forces11. It undergoes a second-order CDW transition at TC ~ 205 K to a commensurate (2 × 2 × 2) superlattice7,9. There is no relevant Fermi surface nesting, and the traditional picture of Peierls’ instability or coupling via Kohn anomalies does not apply, but the nature of the transition remains under intense debate12,13,14,15,16,17. The crystal in the normal state possesses a small indirect gap. Referring to the pictures of the Brillouin zones for both the normal and CDW phases shown in Fig. 1B–D, the top of the valence band, located at the Γ point, is of the Se 4p character, and the bottom of the conduction band, located at the L point, is of the Ti 3d character. An early theory invoked an excitonic interaction across the gap, which leads to band folding, gap widening, and energy minimization16,18. A more recent view is that a (2 × 2 × 2) lattice distortion causes the Se 4p and the Ti 3d states across the gap to couple via the crystal potential of the distorted lattice3,14,16. The mathematical formulation is similar for the two cases, but the underlying physics is different. In the latter case, the transition is purely a band-structure effect, requiring no higher-order electronic interactions; the coupled electron-lattice system evolves, or distorts, to minimize the total energy.
Crystal structure and electronic band structure of TiSe2 measured by ARPES.
(A) Crystal structure of bulk TiSe2. (B) Three-dimensional Brillouin zones of the (1 × 1 × 1) and (2 × 2 × 2) structures outlined in black and red, respectively. (C) Projected two-dimensional Brillouin zones in the basal plane. (D) Projected two-dimensional Brillouin zones in a vertical plane. (E) ARPES intensity maps at various energies taken with 58 eV photons for the normal phase at 300 K and the CDW phase at 10 K.
Our systematic three-dimensional band structure mapping of this system using angle-resolved photoemission spectroscopy (ARPES) proves that the above picture focusing on a single (2 × 2 × 2) coupling is incorrect or too simplistic. Aided by first-principles calculations, we show that while the band dispersion is weak along z (perpendicular to the layers), its contribution to the total energy difference between the normal and CDW phases is not negligible. A further impetus for our reinvestigation is the recent report of a (2 × 2) CDW transition in single-layer TiSe219,20, which provided an intriguing clue about the bulk transition. Specifically, a speculation was that the three-dimensional transition might involve a hidden two-dimensional order never considered or detected before. Indeed, our results reveal a number of surprises. A hitherto undetected (2 × 2) two-dimensional electronic order sets in at ~232 K before the known three-dimensional structural transition at ~205 K. The system does not become a direct-gap semiconductor as widely assumed previously based on the (2 × 2 × 2) folding of the conduction band minimum at the L point back to the Γ point. Rather, the system remains an indirect-gap semiconductor because the valence band maximum shifts from Γ to A*.
Results
Electronic band structure in the normal and CDW phases
A set of ARPES intensity maps at various energies below the Fermi level (Fig. 1E) shows the evolution of the bands, where kx and ky point along the  and
and  directions, respectively. For the normal phase at 300 K, emission from the Se 4p states appears as a circle centered at
directions, respectively. For the normal phase at 300 K, emission from the Se 4p states appears as a circle centered at  at energies near the Fermi level; it become a hexagon and then a warped hexagon with additional details at energies farther away from the Fermi level. Similar features are evident for the CDW phase at 10 K; additionally, a weak replica by (2 × 2 × 2) folding of the Se 4p bands is clearly seen centered at
at energies near the Fermi level; it become a hexagon and then a warped hexagon with additional details at energies farther away from the Fermi level. Similar features are evident for the CDW phase at 10 K; additionally, a weak replica by (2 × 2 × 2) folding of the Se 4p bands is clearly seen centered at  =
=  (kx = 0 and ky = 1.03 Å–1). Furthermore, a tiny circle appears at
(kx = 0 and ky = 1.03 Å–1). Furthermore, a tiny circle appears at  =
=  at the Fermi level, which comes from the Ti 3d conduction band minimum. Such measurements were repeated for many photon energies in order to systematically change the kz of the initial state; here, we make use of a free-electron approximation for the final band, with the inner potential set at 13 eV.
at the Fermi level, which comes from the Ti 3d conduction band minimum. Such measurements were repeated for many photon energies in order to systematically change the kz of the initial state; here, we make use of a free-electron approximation for the final band, with the inner potential set at 13 eV.
Calculated band structure
A calculated HSE band structure is presented in Fig. 2A for the normal phase. The Se 4p valence band maximum at Γ and the Ti 3d conduction band minimum at L are separated by a negative gap of 0.36 eV, which differs from the experimental value of +0.039 eV (Fig. 3A). This calculation assumes a frozen (1 × 1 × 1) structure at T = 0, but this is not a stable or the ground-state structure. Thus, the computed band structure including the gap is just an approximation and should not be expected to accurately describe the experimental results for the (1 × 1 × 1) phase that exists only at T > TC. By contrast, there is no such concern for the (2 × 2 × 2) CDW phase at very low temperatures. The calculation (Fig. 2B) shows that the L point is back folded to the zone center, and the Ti 3d conduction band minimum is now repeated at the zone center. The CDW interaction pushes the Se 4p valence band maximum at Γ to a lower energy, resulting in a positive gap. This energy lowering interaction at Γ leaves the nearby A* point at a higher energy, which becomes the new valence band maximum. The system in the CDW phase remains an indirect-gap semiconductor, contrary to the long-held assumption of a direct-gap semiconductor.
Three dimensional band mapping of TiSe2.
ARPES spectra for (A) the normal phase at 300 K and (B) the CDW phase at 10 K along various directions as labeled. Some experimental band edge energies are indicated. The photon energies used were 58, 75, 46, and 67 eV for the data centered about Γ, A, L, and A*, respectively. (C) and (D) are ARPES intensity maps as a function of kz or photon energy for the normal and CDW phases, respectively. The yellow dotted curve for each case marks the experimental dispersion relation of the topmost valence band, obtained by fitting to the energy- or momentum-distribution curves. In all cases, the white dashed curves are calculated bands shifted in energy by matching the experimental Ti 3d band bottom or Se 4p band top where appropriate. The energy shifts for the valence and conductions bands are −345 and 30 meV for the normal phase, and −90 and −80 meV for the CDW phase, respectively.
ARPES maps and perpendicular dispersion
Detailed band mapping results centered about Γ, A, L, and A* along major symmetry directions are presented in Fig. 3A and B for the normal and CDW phases with the sample at 300 and 10 K, respectively. The energies of the valence band maximum and conduction band minimum are marked. The photon energies used were 58, 75, 46, and 67 eV for the data centered about Γ, A, L, and A*, respectively. For comparison, the calculated band dispersion relations are shown as white dashed curves, shifted in energy where appropriate by matching the experimental Ti 3d band bottom or the Se 4p band top. The experimental conduction band minimum at L/Γ* dips just below the Fermi level in both the normal and CDW phases at nearly the same energy. Also observed is a weak replica of the Se 4p valence bands centered about L in the CDW phase due to zone repeating. A fuzzy remnant of the replica bands can be seen for the normal phase, which has been attributed to fluctuation effects18 and can be related to the fuzzy x-ray thermal diffuse scattering peaks centered about the superlattice Bragg positions21.
Figure 3C and D present ARPES maps of the top valence bands as a function of kz at kx = ky = 0, obtained by scanning the photon energy, for the normal and CDW phases, respectively. The experimental dispersion for the topmost valence band is indicated by a yellow dotted curve in each case; also shown is the theoretical dispersion (white dashed curve). For the CDW phase, the agreement is excellent, including the x2 periodicity. The valence band maximum is indeed at the A* point, and the effective mass at Γ is reversed, as the theory predicts. The theoretical indirect gap is 0.07 eV, in close agreement with the experimental value of 0.082 eV.
Temperature dependence of the band gap and determination of the transition temperatures
Figure 4 shows the experimental temperature dependence of the valence band edge energies at Γ, A, and A* relative to the conduction band minimum at L as the sample is cooled from the normal phase into the CDW phase. Once the CDW phase sets in, points A and L both become Γ*, but the band folding effects are weak for the small lattice distortion, and the parentage of each band remains largely unaffected. Plotted in Fig. 4A–C are squares of the three gap energies, Δ(Γ), Δ(A), and Δ(A*). All three cases show a gap widening transition as the temperature lowers, but the onset temperatures are not the same. Figure 4D–F show zoom-in views near the onsets. The square of the gap energy is expected to follow a mean field behavior for T near but below TC:
Temperature-dependent band gaps and transition temperatures.
The data points represent square of the experimental energy gap between the conduction band bottom at L and the valence band top at (A) Γ, (B) A, and (C) A* as a function of temperature. The energy of each band at each k point is determined from fitting to the energy- or momentum-distribution curves. The error bar is deduced from the standard deviation of the fitting. The red curves are fits. (D–F) present corresponding detailed views near the onset. The transition temperatures TC1 and TC2 deduced from fitting are indicated. The bulk transition at TC2 is indicated by a green vertical dashed line.

This linear onset is evident in the data and permits a precise determination of the transition temperature. The red curves in Fig. 4 are fits using a semi-empirical BCS-type gap equation20, which reduces to a linear function near the onset. Figure 4D shows that the onset of Δ(Γ) is at TC2 ~ 205 K, which agrees well with the known bulk transition temperature. On the other hand, the gaps Δ(A) and Δ(A*) show a substantially higher onset temperature TC1, which agrees closely with the (2 × 2) transition temperature of TC0 = 232 ± 5 K found in single-layer TiSe220. The implication is that the CDW transition in bulk TiSe2 actually consists of two stages. Upon lowering the temperature, the first transition involves a (2 × 2) ordering of each individual layer at TC1, but the CDW order in neighboring layers is phase uncorrelated. The second transition involves an anti-phase locking of neighboring layers at TC2 to form the (2 × 2 × 2) structure.
Discussion
An intermediate partially-ordered phase between TC1 and TC2 is entirely consistent with the highly anisotropic nature of the system. Referring to Fig. 3C, the nearly flat experimental dispersion for the top valence band between Γ and A in the normal phase suggests that a (2 × 2 × 2) superlattice modulation connecting Γ and L and a (2 × 2 × 1) superlattice modulation connecting A and L can be both important for driving the CDW transition. In view of the higher transition temperature for the single layer, it is reasonable that bulk TiSe2 undergoes (2 × 2) transitions in individual layers first. This transition involves the coupling between A and L, and so the corresponding gap Δ(A) shows an onset at the single-layer transition temperature TC1 = TC0 as seen in experiment. The period doubling along z mediated by the van der Waals interlayer coupling is expected to be a weaker effect, and it happens at the lower bulk transition temperature TC2. Because the (2 × 2 × 2) ordering involves the coupling between Γ and L, the gap Δ(Γ) should show an onset at TC2 as seen in Fig. 4D. The data seem to show a hint of a tiny onset at TC1 as well, but it is about the size of the noise. The gap Δ(A*) involves both the (2 × 2 × 1) and (2 × 2 × 2) coupling, and a single-component fit is not necessarily accurate, but the dominant effect should come from the stronger transition at TC1 as seen in Fig. 4F.
Calculations for the two different stacking patterns, (2 × 2 × 1) and (2 × 2 × 2), yield energy lowering per chemical unit of 3 and 4 meV, respectively, relative to the (1 × 1 × 1) structure. The closeness of the two energies suggests that the two-dimensional (2 × 2) distortion is the main driver of the CDW phase. The x2 stacking along z lowers the energy a little further, and experimentally it happens at a lower temperature. Theoretical calculations based on energy minimization reveals no energy barriers because the distortion pattern is simple with a monotonic lowering of the energy toward the minimum. The partially ordered intermediate phase between TC1 and TC2 does not necessarily reveal itself in standard diffraction measurements because of the random stacking of the (2 × 2) layers; static long-range structural correlation is needed for superlattice reflection. Indeed, this hidden electronic order has never been detected before by diffraction.
The presence of two transitions associated with two different energy gaps indicates that the CDW transition in TiSe2 can be attributed to electron-lattice coupling with a dimensional crossover. A transition, either (2 × 2) within the layers or (2 × 2 × 2) for the three-dimensional organization, leads to band folding, renormalization of the band shapes, and widening of the gaps. The last effect contributes directly to energy lowering of the system. The overall CDW transition is a three-dimensional phenomenon, but it exhibits a strong two-dimensional driver that leads to a separate transition. While the Fermi level lies slightly above the conduction band bottom for both the normal and CDW phases because of n-type self-doping, Fermi surface nesting does not appear to play a role and the system remains a doped indirect-gap semiconductor after the transition. Given the prototypical status of TiSe2 within the very large class of CDW transition metal dichalcogenides with similar layered structures, the findings reported herein are likely general and relevant to the development of a comprehensive understanding of the physical behavior of these materials in terms of dimensional effects.
Methods
Experimental Details
High quality TiSe2 single crystals were synthesized by iodine-vapor transport with excess Se21. The samples are semimetallic in agreement with prior studies and our own photoemission measurements. This behavior can be attributed to n-type self-doping of the material caused by Se vacancies. This self-doping effect is common in layered selenides including Bi2Se322 and SnSe23. ARPES measurements were performed at beamlines 12.0.1 and 10.0.1, Advanced Light Sources, Lawrence Berkeley National Laboratory, using samples freshly cleaved in situ. The system energy resolution was less than 20 meV, and the angular resolution was 0.2°. The in-plane orientation of the sample was precisely determined from the symmetry of the measured constant-energy ARPES maps. The sample temperature was maintained at 300 and 10 K, respectively, for the normal and CDW phases, except during temperature scans. ARPES Measurements were made using photon energies ranging from 30 to 100 eV in order to systematically vary kz, the momentum component along the surface normal. We assume a free-electron final band dispersion relation shifted by an inner potential, which should work well for the photon energy range used in the experiment10,24,25. The inner potential was set empirically to 13 eV, a typical and reasonable value, in order to place the band extrema at the expected zone center or boundary points.
Theoretical Calculations
First-principles calculations were performed using the Vienna ab initio package (VASP)26,27,28 with the projector augmented wave method29,30. We included the semi-core 3p electrons of Ti in the calculation. With an energy cutoff of 320 eV for the plane wave expansion of the wave functions, the system energy converged to better than 1 meV per chemical unit. A k-mesh of 18 × 18 × 18 (9 × 9 × 9) was used in the self-consistent calculations for the normal (CDW) phase. The computed phonons in the normal phase exhibited instabilities near the L and M points, in agreement with previous results3. A CDW distortion pattern was constructed by including all symmetry-related soft modes at L, which was then further refined by energy minimization using the generalized gradient approximation (GGA) with the Perdew-Burke-Ernzerhof (PBE) functional31. A test calculation based on PBE was performed first for a monolayer TiSe2, which resulted in an optimized lattice constant of a = 3.538 Å. This value agrees well the experimental value of a = 3.534 Å for bulk TiSe2. Since PBE is known to have difficulties in predicting the interlayer separation in layered structures with the van der Waals interaction between the layers, the experimental lattice constants a = 3.534 Å and c = 6.008 Å were used for further optimization of the atomic coordinates for the CDW phase. The final optimized distortion pattern is shown in Fig. S1. It has a lower energy than the normal phase by 4 meV per TiSe2 chemical unit. Similar energy lowering was also obtained by using the local density approximation (LDA) with the experimental lattice constants. Our results are consistent with prior reports3,32.
Additional Information
How to cite this article: Chen, P. et al. Hidden Order and Dimensional Crossover of the Charge Density Waves in TiSe2. Sci. Rep. 6, 37910; doi: 10.1038/srep37910 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Gerber, S. et al. Three-dimensional charge density wave order in YBa2Cu3O6.67 at high magnetic fields. Science 350, 949–952 (2015).
Chang, J. et al. Direct observation of competition between superconductivity and charge density wave order in YBa2Cu3O6.67 . Nature Phys. 8, 871–876 (2012).
Calandra, M. & Mauri, F. Charge-density wave and superconducting dome in TiSe2 from electron-phonon interaction. Phys. Rev. Lett. 106, 196406 (2011).
Joe, Y. I. et al. Emergence of charge density wave domain walls above the superconducting dome in 1T-TiSe2 . Nature Phys. 10, 421–425 (2014).
Wi1son, J. A., DiSalvo, F. J. & Mahajan, S. Charge-density waves and superlattices in the metallic layered transition metal dichalcogenides. Adv. Phys. 24, 117–201 (1975).
Grüner, G. The dynamics of charge-density waves. Rev. Mod. Phys. 60, 1129–1181 (1988).
Rossnagel, K. On the origin of charge-density waves in select layered transition-metal dichalcogenides. J. Phys. Condens. Matter 23, 213001 (2011).
Zhu, X., Cao, Y., Zhang, J., Plummer, E. W. & Guo, J. Classification of charge density waves based on their nature. Proc. Nat. Acad. Sci. USA 112, 2367–2371 (2015).
Di Salvo, F. J., Moncton, D. E. & Waszczak, J. V. Electronic properties and superlattice formation in the semimetal TiSe2 . Phys. Rev. B 14, 4321–4328 (1976).
Anderson, O., Manzke, R. & Skibowski, M. Three-dimensional and relativistic effects in layered 1 T-TiSe2 . Phys. Rev. Lett. 55, 2188–2191 (1985).
Rossnagel, K. Suppression and emergence of charge-density waves at the surfaces of layered 1T-TiSe2 and 1T-TaS2 by in situ Rb deposition. New J. Phys. 12, 125018 (2010).
Coleman, R. et al. Scanning tunnelling microscopy of charge-density waves in transition metal chalcogenides. Adv. Phys. 37, 559–644 (1988).
Kusmartseva, A. F., Sipos, B., Berger, H., Forró, L. & Tutiš, E. Pressure induced superconductivity in pristine 1T−TiSe2 . Phys. Rev. Lett. 103, 236401 (2009).
Kidd, T. E., Miller, T., Chou, M. Y. & Chiang, T.-C. Electron-hole coupling and the charge density wave transition in TiSe2 . Phys. Rev. Lett. 88, 226402 (2002).
May, M. M., Brabetz, C., Janowitz, C. & Manzke, R. Charge-density-wave phase of 1T−TiSe2: the influence of conduction band population. Phys. Rev. Lett. 107, 176405 (2011).
Rossnagel, K., Kipp, L. & Skibowski, M. Charge-density-wave phase transition in 1T−TiSe2: Excitonic insulator versus band-type Jahn-Teller mechanism. Phys. Rev. B 65, 235101 (2002).
van Wezel, J., Nahai-Williamson, P. & Saxena, S. S. Exciton-phonon-driven charge density wave in TiSe2 . Phys. Rev. B 81, 165109 (2010).
Cercellier, H. et al. Evidence for an Excitonic Insulator Phase in 1T-TiSe2 . Phys. Rev. Lett. 99, 146403 (2007).
Peng, J.-P. et al. Molecular beam epitaxy growth and scanning tunneling microscopy study of TiSe2 ultrathin films. Phys. Rev. B 91, 121113 (2015).
Chen, P. et al. Charge density wave transition in single-layer titanium diselenide. Nat. Commun. 6, 8943 (2015).
Holt, M., Zschack, P., Hong, H., Chou, M. Y. & Chiang, T.-C. X-Ray studies of phonon softening in TiSe2 . Phys. Rev. Lett. 86, 3799–3802 (2001).
Koleini, M., Frauenheim, T. & Yan, B. Gas Doping on the Topological Insulator Bi2Se3 Surface. Phys. Rev. Lett. 110, 016403 (2013).
Wang, Z. et al. Molecular Beam Epitaxy-Grown SnSe in the Rock-Salt Structure: An Artificial Topological Crystalline Insulator Material. Adv. Mat. 27, 4150–4154 (2015).
Damascelli, A., Hussain, Z. & Shen, Z.-X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 75, 473–541 (2003).
Chiang, T.-C., Knapp, J. A., Aono, M. & Eastman, D. E. Angle-resolved photoemission, valence-band dispersions E( ), and electron and hole lifetimes for GaAs. Phys. Rev. B 21, 3513–3522 (1980).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 48, 13115–13118 (1993).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Bianco, R., Calandra, M. & Mauri, F. Electronic and vibrational properties of TiSe2 in the charge-density-wave phase from first principles. Phys. Rev. B 92, 094107 (2015).
Acknowledgements
This work is supported by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, Division of Materials Science and Engineering, under Grant No. DE-FG02-07ER46383 (TCC) and the National Science Foundation Grant No. EFMA-1542747 (MYC). The Advanced Light Source is supported by the Director, Office of Science, Office of Basic Energy Sciences, U.S. DOE under Contract No. DE-AC02-05CH11231. YHC is supported by a Thematic Project at Academia Sinica.
Author information
Authors and Affiliations
Contributions
P.C. with the aid of X.Y.F., S.K.M., Z.H., A.V.F. and T.C.C. performed ARPES measurements and data analysis. Y.H.C. and M.Y.C. performed first-principles calculations. P.C. and T.C.C. wrote the paper. T.C.C., P.C. and M.Y.C. interpreted the data. T.C.C. and A.V.F. jointly led the experimental project.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Chen, P., Chan, YH., Fang, XY. et al. Hidden Order and Dimensional Crossover of the Charge Density Waves in TiSe2. Sci Rep 6, 37910 (2016). https://doi.org/10.1038/srep37910
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep37910
This article is cited by
-
Ultrafast formation of topological defects in a two-dimensional charge density wave
Nature Physics (2024)
-
Light-induced hexatic state in a layered quantum material
Nature Materials (2023)
-
Charge density wave order and electron-boson coupling in ternary superconductor Bi2Rh3Se2
Science China Physics, Mechanics & Astronomy (2023)
-
Light-induced dimension crossover dictated by excitonic correlations
Nature Communications (2022)
-
Importance of charge self-consistency in first-principles description of strongly correlated systems
npj Computational Materials (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.