Abstract
Non-centrosymmetric superconductors, whose crystal structure is absent of inversion symmetry, have recently received special attentions due to the expectation of unconventional pairings and exotic physics associated with such pairings. The newly discovered superconductors A2Cr3As3 (A = K, Rb), featured by the quasi-one dimensional structure with conducting CrAs chains, belongs to such kind of superconductor. In this study, we are the first to report the finding that superconductivity of A2Cr3As3 (A = K, Rb) has a positive correlation with the extent of non-centrosymmetry. Our in-situ high pressure ac susceptibility and synchrotron x-ray diffraction measurements reveal that the larger bond angle of As-Cr-As (defined as α) in the CrAs chains can be taken as a key factor controlling superconductivity. While the smaller bond angle (defined as β) and the distance between the CrAs chains also affect the superconductivity due to their structural connections with the α angle. We find that the larger value of α-β, which is associated with the extent of the non-centrosymmetry of the lattice structure, is in favor of superconductivity. These results are expected to shed a new light on the underlying mechanism of the superconductivity in these Q1D superconductors and also to provide new perspective in understanding other non-centrosymmetric superconductors.
Similar content being viewed by others
Introduction
The unconventional superconductors containing 3d-electrons possess intriguing superconductivity and other exotic properties, which provide an excellent platform to reveal the underlying superconducting mechanism and electron correlated physics. After the discovery of the two main families of copper oxide and iron-based superconductors1,2,3, a new family of CrAs-based superconductors A2Cr3As3 (A = K, Rb and Cs) were discovered recently4,5,6. The superconducting transition temperature (Tc) is found to be ~6.1 K in K2Cr3As34,7, 4.8 K in Rb2Cr3As35,8, and 2.2 K in Cs2Cr3As36 respectively. They are the only compounds found to hold superconductivity at ambient pressure in Cr-based superconductors so far9. Remarkably, these new superconductors exhibit unconventional properties, including non-Fermi liquid behaviors in its normal state and an unusual large value of the upper critical field at zero temperature4,7,10,11,12,13,14,15.
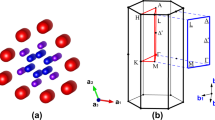
Structurally, these new superconductors bear a common quasi-one-dimensional (Q1D) configuration originated from the one dimensional CrAs chains that crystallize in a fashion of double-wall subnano-tubes (the inner-wall tube are constructed by Cr-Cr-Cr (defined as Cr3) triangles and the outer-wall tube by As-As-As (defined as As3) triangles), with the alkali metal ions located among the interstitials of the CrAs chains4,5,6. Theoretical studies propose that these CrAs chains may play a crucial role in stabilizing the superconductivity16,17,18,19,20. We noted that the alternative distribution of alkali metal ions along the chain direction give rise to a larger and a smaller bond angles of As-Cr-As, defined as As2-Cr2-As2 (α) and As1-Cr1-As1 (β) respectively, as shown in Fig. 1. Therefore the A2Cr3As3 (A = K and Rb) with asymmetric distribution of the alkali metal ions can be structurally classified as non-centrosymmetric superconductors21. In order to clarify the correlation between the superconductivity and characteristic lattice parameters, we performed high pressure investigations on the K2Cr3As3 and Rb2Cr3As3 superconductors in this study as pressure is an effective way to change the lattice structure, affect the extent of the non-centrosymmetry and result in the corresponding change of superconducting properties22,23,24.
(a) Schematic crystal structure of K2Cr3As3. In crystallographic description, K2Cr3As is constructed with the double-walled subnano-tubes of Cr and As ions. (b) The views of lattice structure parallel to the ac plane. (c) Alternative distribution of K1 and K2 ions between layers. (d) Sketch of the two different bond angles in CrAs chains.
Figure 2a and b show the ac susceptibility measurements on the K2Cr3As3 single crystal under hydrostatic pressure. The diamagnetic signals from superconducting transitions of the sample and the Pb (as a pressure gauge) are clearly demonstrated in the plots of temperature dependence of the real part (χ′). The first drops displayed at higher temperature are the diamagnetic signals from the Pb, and the second drops at lower temperature are from the sample. It can be seen that the Tc of the sample shifts to lower temperature upon increasing pressure (Fig. 2a). At pressure ~4.83 GPa, the Tc decreases to 2.72 K. On pressure unloading, the Tc recovers by tracing the route of the Tc change with pressure increment (Fig. 2a and b). The superconducting behaviors of Rb2Cr3As3 are also investigated under the hydrostatic pressure. Its real part of the ac susceptibility versus temperature is plotted in Fig. 2c (pressure loading) and Fig. 2d (pressure unloading). It is obvious that the pressure drives all the Tcs decrease monotonically (Fig. 2a and c). In addition, the decreased Tcs with pressure loading are recoverable for both of the superconductors.
To understand the pressure effect on the structure and the corresponding Tc in these Q1D superconductors, as well as uncover the key factor that controls superconductivity, we performed in-situ high pressure synchrotron x-ray diffraction (HP-XRD) measurements for K2Cr3As3 and Rb2Cr3As3 (Fig. 3). We find no pressure-induced structural phase transition in these two kinds of samples over the pressure range investigated. As shown in Fig. 3a and f, the samples stabilize in the ambient-pressure structure of hexagonal unit cell in P m2 (No. 187) space group4,5. The normalized lattice parameters, a/ao and c/co, exhibit linear pressure dependence, and the plots of pressure dependent volume show no obvious discontinuity for both of the K2Cr3As3 and Rb2Cr3As3 (Fig. 3b,c and g,h). However, we find that the lattice parameter a of K2Cr3As3 is compressed by ~5%, while the c is reduced by ~2% at the same pressure of 8.16 GPa. As for Rb2Cr3As3, the lattice parameter a is compressed by ~5.5%, while the c is reduced by ~3.2% at the pressure of 8.57 GPa. Although these results seems to be common phenomenon for a one or a two dimensional system, the effect of the anisotropic shrinkage on such kinds of non-centrosymmery systems investigated here is a new issue which needs to be studied in detail. Based on these XRD data, we performed further analysis for the XRD profiles using Rietveld method and the RIETAN-FP program25,26. Pressure dependences of the distances of Cr1-Cr1 (or Cr2-Cr2) (defined as Lcr1-cr1 and Lcr2-cr2) and As1-As1(or A2-As2) (defined as LAs1-As1 and LAs2-As2) are obtained. It can be seen that either Lcr1-cr1 and Lcr2-cr2 or LAs1-As1 and LAs2-As2 are decreased upon increasing pressure (Fig. 3d,e and i,j), however, the LAs1-As1 and the LAs2-As2 display more pronounced reduction than the Lcr1-cr1 and the Lcr2-cr2. The larger reduction of the LAs-As directly leads to an increase both in the α angle and the β angle, as shown in Fig. 1.
m2 (No. 187) space group4,5. The normalized lattice parameters, a/ao and c/co, exhibit linear pressure dependence, and the plots of pressure dependent volume show no obvious discontinuity for both of the K2Cr3As3 and Rb2Cr3As3 (Fig. 3b,c and g,h). However, we find that the lattice parameter a of K2Cr3As3 is compressed by ~5%, while the c is reduced by ~2% at the same pressure of 8.16 GPa. As for Rb2Cr3As3, the lattice parameter a is compressed by ~5.5%, while the c is reduced by ~3.2% at the pressure of 8.57 GPa. Although these results seems to be common phenomenon for a one or a two dimensional system, the effect of the anisotropic shrinkage on such kinds of non-centrosymmery systems investigated here is a new issue which needs to be studied in detail. Based on these XRD data, we performed further analysis for the XRD profiles using Rietveld method and the RIETAN-FP program25,26. Pressure dependences of the distances of Cr1-Cr1 (or Cr2-Cr2) (defined as Lcr1-cr1 and Lcr2-cr2) and As1-As1(or A2-As2) (defined as LAs1-As1 and LAs2-As2) are obtained. It can be seen that either Lcr1-cr1 and Lcr2-cr2 or LAs1-As1 and LAs2-As2 are decreased upon increasing pressure (Fig. 3d,e and i,j), however, the LAs1-As1 and the LAs2-As2 display more pronounced reduction than the Lcr1-cr1 and the Lcr2-cr2. The larger reduction of the LAs-As directly leads to an increase both in the α angle and the β angle, as shown in Fig. 1.
(a) X-ray diffraction patterns of K2Cr3As3 at different pressures. (b) and (c) Pressure dependences of the normalized lattice constants a/a0, c/c0 and the volume of K2Cr3As3. (d) and (e) Distances of As-As ions and Cr-Cr ions as a function of pressures for K2Cr3As3. (f) X-ray diffraction patterns of Rb2Cr3As3 at different pressures. (g) and (h) Plots of the normalized lattice constants a/a0, c/c0 and the volume versus pressures for Rb2Cr3As3. (i) and (j) Pressure dependent distances of As-As ions and Cr-Cr ions for Rb2Cr3As3.
The importance of the anion-cation-anion angles for the superconductivity in compounds with ionic bonds, such as FeAs-based superconductors, is broadly studied and accepted27,28,29,30,31,32. It is also known that these angles can be tuned by either chemical doping or external pressure. From our HP-XRD results, we find that there exist correlations between the Tc and the bond angles of α and β, as shown in Fig. 4a and b. It is seen that the Tc in K2Cr3As3 and Rb2Cr3As3 can be scaled well only by the α angle (Fig. 4a), but fail to be scaled by the β angle (Fig. 4b). These results suggest that the α angle seems to be a key factor controlling the superconducting temperature for these two materials. However, it is unreasonable to neglect the effect of β angle on superconductivity because the coexistence of the two distinct bond angles (α and β angles, α > β) result in the appearance of superconductivity in A2Cr3As3. This has been clarified by comparisons with the lattice feature and corresponding property of its sister compound ACr3As333,34. Structurally, ACr3As3 possesses a single Cr-As-Cr bond angle (α = β) and is a centrosymmetric compound, which is found to be non-superconducting33,34. Therefore, it is believable that the β angle in A2Cr3As3 should cooperatively determine the extent of non- centrosymmetry with the α angle, so that the β angle must play a vital role for developing and tuning the superconductivity. In fact, the β angle changes with pressure together with the α angle, thus the combined effect of α and β angles on the superconductivity is one of the key issues to understand these superconductors.
(a) and (b) α and β angles versus Tc for A2Cr3As3 (A = K and Rb) superconductors. (c) to (e) Pressure dependences of Tc, α-β and LCrAs for K2Cr3As3 superconductor. (f) to (h) Tc, α-β and LCrAs as a function of pressure for Rb2Cr3As3 superconductor. The solid triangles in (c) are the data taken from ref. 7. The open circles in (c,f) represent Tc obtained from our A2Cr3As3 samples upon loading and unloading, respectively. The solid squares in (f) are the data taken from ref. 5. (d) and (g) Pressure dependence of α-β angle for the samples investigated. (e) and (h) The distance between CrAs chains (LCrAs) as a function of pressure for K2Cr3As3 and Rb2Cr3As3, respectively.
In order to clarify the correlation between the extent of non-centrosymmetry and Tc in these Q1D superconductors, we established the pressure dependences of Tc for K2Cr3As3 and Rb2Cr3As3 respectively (Fig. 4c–g). Apparently, the change of the α-β value with pressure follows the same tendency for these two kinds of superconductors, declining almost linearly upon increasing pressure (Fig. 4d and g) and exhibits the same trend as that of pressure dependence of Tc. Furthermore, it is found that the superconductivity cannot be stabilized as the value of α-β is smaller than 0.722° for K2Cr3As3 superconductor and 1.293° for Rb2Cr3As3 superconductor respectively. Our results reveal that a higher non-centrosymmetry is in favor of superconductivity of these Q1D superconductors. Significantly, we note that the absolute value of the angle difference in Rb2Cr3As3 is bigger than that of K2Cr3As3 at the same pressure, while its ambient-pressure Tc of Rb2Cr3As3 is lower than that of K2Cr3As3 (Fig. 4c and d, f and g), which indicates that the difference of the two bond angles α-β cannot be taken as a unique structural control parameter for the superconductivity of the two kinds of superconductors, indicating that there is another factor impacting on the superconductivity. Consequently, we plot pressure dependence of the distance between the CrAs chains (LCrAs), as shown in Fig. 4e and h. It is found that the LCrAs indeed is relevant to the superconductivity for a given superconductor of K2Cr3As3 or Rb2Cr3As3, and that the smaller LCrAs between the two superconductors benefits a higher Tc. Our data indicate that the superconductivity in A2Cr3As3 can be scaled by α angle which is structurally connected with β angle and LCrAs. The precise explanation for this issue deserves further investigations.
We estimate the electron density distribution (EDD) for K2Cr3As3 based on our HP-XRD data collected at different pressures, mainly focusing on the EDD of the two sites of Cr ions, to understand how the bond angle difference or the extent of non-centrosymmetry influences the distribution of electrons. As shown in Fig. 5a and b, the EDD of Cr2 ion is obviously lower than that of Cr1 ions. For comparison, we define this difference as ΔEDD = EDDCr1 − EDDCr2 and plot the pressure dependences of ΔEDD and Tc respectively (Fig. 5c). Remarkably, the ΔEDD and the corresponding Tc decrease with increasing pressure, revealing that the extent of inhomogeneous electron state originated from the change of non-centrosymmetric lattice structure is the intrinsic factor for developing/stabilizing the superconductivity in this kind of Q1D superconductors.
(a) and (b) Two dimensional (2D) distribution of electron density on K1-Cr2-As2 and K2-Cr1-As1 layers at 1.35 GPa and 3.39 GPa. The 2D-EDD on the (001) lattice plane was calculated by MEM. The color gradient from blue to red represents the EDD gradient from 0% to 40% (here we set 40% as the maximum value for the EDD). The contour lines are drawn from 0.2e Å−3 to 24.2e Å−3 with 2e Å−3 intervals. (c) Pressure dependences of difference of electron density distribution (∆EDD = EDDCr1 − EDDCr2) at two sites of Cr ions, and Tc for K2Cr3As3.
In summary, we are the first to report that the extent of non-centrosymmetry has a positive effect on developing or stabilizing the superconductivity in A2Cr3As3 (A = K, Rb), a new kind of unconventional superconductor with Q1D feature. Our high pressure studies demonstrate that, among the characteristic parameters, α, β, α-β and LCrAs, the α angle appears to be the scaling parameter for the Tcs in A2Cr3As3 superconductors. While a larger value of α-β angle is in favor of the superconductivity for a given superconductor K2Cr3As3 or Rb2Cr3As3 and a smaller LCrAs between these two different superconductors benefits a higher Tc. The precise explanation for the connection between the α angle and α-β as well as LCrAs deserves further investigations. The influences of the bond angles and the distance between the chains on the superconductivity in these Q1D CrAs-based superconductors are reminiscent what has been seen in the 2D FeAs-based superconductors, in which the As-Fe-As bond angle and the coupling between FeAs layers are the key factors governing the Tc cooperatively27,28,29,30,31,35,36,37 and these factors can also be tuned by applying pressure23,24,28,38. Therefore, further studies on the common features shared by these Q1D and 2D arsenide superconductors may be helpful to understand the underlying mechanism of the superconductivity in the compounds containing 3d-electrons in a unified way.
Method
The K2Cr3As3 single crystals were prepared by the flux method as described in ref. 4. The Rb2Cr3As3 polycrystalline samples are synthesized by solid reaction method, as described in ref. 5. Hydrostatic pressure ac susceptibility measurements were performed in a Toroid-type high pressure cell (THPC)39, and Daphne 7373 (liquid) was used as the pressure transmitting medium. The sample was loaded into a home-made coil which is immersed into the liquid pressure medium in a Teflon capsule and set in the THPC. Pressure is determined by the pressure dependent Tc of Pb40 that is placed in the same coil together with the sample. Angle dispersive x-ray diffraction (XRD) measurements under pressure were carried out at beamline 15U at Shanghai Synchrotron Radiation Facility (SSRF). In the XRD measurements, a monochromatic x-ray beam with a wavelength of 0.61992 Å was adopted and the Daphne 7373 was employed to ensure the sample in the same hydrostatic pressure environment as that in the magnetic measurements. Pressure was determined by the ruby fluorescence method41. Since A2Cr3As3 samples are air sensitive, the sample loading for all high pressure measurements was performed in a glove box that is filled with Ar gas.
For the crystal structure refinements of the high pressure XRD data with the Rietveld method25, the program RIETAN-FP was employed26,42,43,44, and the ambient-pressure lattice parameters of the host sample were used as the initial data. In the refinements, the occupancy for all the positions of atoms was taken as 100%. The electron density distributions (EDD) were determined by maximum entropy method (MEM) based on our XRD data with Dysnomia program45. In the EDD calculations, the unit cell was divided into 132 × 132 × 64 pixels along the three axial directions of the unit cell. The crystal structures and the EDD were visualized using the software package VEST46.
Additional Information
How to cite this article: Wang, Z. et al. Correlation between superconductivity and bond angle of CrAs chain in non-centrosymmetric compounds A2Cr3As3 (A = K, Rb). Sci. Rep. 6, 37878; doi: 10.1038/srep37878 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Bednorz, J. G. & Müller, K. A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. B 64, 189–193 (1986).
Kamihara, Y., Watanabe, T., Hirano, M. & Hosono, H. Iron-Based layered superconductor La[O1−xFx]FeAs (x = 0.05–0.12) with Tc = 26 K. J. Am. Chem. Soc. 130, 3296–3297 (2008).
Hsu, F. C. et al. Superconductivity in the PbO-type structure α-FeSe. PNAS 105, 14262–14264 (2008).
Bao, J. K. et al. Superconductivity in quasi-one-dimensional K2Cr3As3 with significant electron correlations. Phys. Rev. X 5, 011013 (2015).
Tang, Z. T. et al. Unconventional superconductivity in quasi-one-dimensional Rb2Cr3As3 . Phys. Rev. B 91, 020506(R) (2015).
Tang, Z. T. et al. Superconductivity in quasi-one-dimensional Cs2Cr3As3 with large interchain distance. Science China Materials 58, 16–20 (2015).
Kong, T., Bud’ko, S. L. & Canfield, P. C. Anisotropic Hc2, thermodynamic and transport measurements, and pressure dependence of Tc in K2Cr3As3 single crystals. Phys. Rev. B 91, 020507(R) (2015).
Wang, X. F. et al. Tunable electronic anisotropy in single-crystal A2Cr3As3 (A = K, Rb) quasi-one-dimensional superconductors. Phys. Rev. B 92, 020508(R) (2015).
Wu, W. et al. Superconductivity in the vicinity of antiferromagnetic order in CrAs. Nat. Commun. 5, 5508 (2014).
Pang, G. M. et al. Evidence for nodal superconductivity in quasi-one-dimensional K2Cr3As3 . Phys. Rev. B 91, 220502(R) (2015).
Zhi, H. Z., Imai, T., Ning, F. L., Bao, J. K. & Cao, G. H. NMR investigation of the quasi-one-dimensional superconductor K2Cr3As3 . Phys. Rev. Lett. 114, 147004 (2015).
Yang, J., Tang, Z. T., Cao, G. H. & Zheng, G. Q. Ferromagnetic spin fluctuation and unconventional superconductivity in Rb2Cr3As3 revealed by 75As NMR and NQR. Phys. Rev. Lett. 115, 147002 (2015).
Balakirev, F. F. et al. Anisotropy reversal of the upper critical field at low temperatures and spin-locked superconductivity in K2Cr3As3 . Phys. Rev. B 91, 220505(R) (2015).
Adroja, D. T. et al. Superconducting ground state of quasi-one-dimensional K2Cr3As3 investigated using μSR measurements. Phys. Rev. B 92, 134505 (2015).
Zuo, H. K. et al. Dominant spin-triplet superconductivity revealed by the upper-critical-field measurements in K2Cr3As3. arXiv:1511.06169v2 (2016).
Wu, X. X., Le, C. C., Yuan, J., Fan, H. & Hu, J. P. Magnetism in quasi-one-dimensional A2Cr3As3 (A = K,Rb) superconductors. Chin. Phys. Lett. 32, 057401 (2015).
Jiang, H., Cao, G. H. & Cao, C. Electronic structure of quasi-one-dimensional superconductor K2Cr3As3 from first-principles calculations. Scientific Reports 5, 16054 (2015).
Zhong, H. T., Feng, X. Y., Chen, H. & Dai, J. H. Formation of molecular-orbital bands in a twisted hubbard tube: implications for unconventional superconductivity in K2Cr3As3 . Phys. Rev. Lett. 115, 227001 (2015).
Zhou, Y., Cao, C. & Zhang, F. C. Theory for superconductivity in alkali chromium arsenides A2Cr3As3 (A = K,Rb,Cs). arXiv:1502.03928v2 (2015).
Wu, X. X., Yang, F., Le, C. C., Fan, H. & Hu, J. P. Triplet pz-wave pairing in quasi-one-dimensional A2Cr3As3 superconductors (A = K,Rb,Cs). Phys. Rev. B 92, 104511 (2015).
Kneidinger, F. et al. Superconductivity in non-centrosymmetric materials. Physica C 514, 388–398 (2015).
Yi, W. et al. Pressure effect on superconductivity of iron-based arsenic-oxide ReFeAsO0.85 (Re = Sm and Nd). Europhys. Lett. 83, 57002 (2008).
Margadonna, S. et al. Pressure evolution of the low-temperature crystal structure and bonding of the superconductor FeSe (Tc = 37 K). Phys. Rev. B 80, 064506 (2009).
Mito, M. et al. Response of superconductivity and crystal structure of LiFeAs to hydrostatic pressure. J. Am. Chem. Soc. 131, 2986–2992 (2009).
Rietveld, H. M. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 2, 65–71 (1969).
Izumi, F. & Momma, K. Three-dimensional visualization in powder diffraction. Solid State Phenom. 130, 15–20 (2007).
Lee, C. H. et al. Effect of structural parameters on superconductivity in fluorine-free LnFeAsO1−y (Ln = La, Nd). J. Phys. Soc. Jpn. 77, 083704 (2008).
Liu, Q. Q. et al. Pressure-induced isostructural phase transition and correlation of FeAs coordination with the superconducting properties of 111-type Na1−xFeAs. J. Am. Chem. Soc. 133, 7892–7896 (2011).
Johnston, D. C. The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides. Advances in Physics 59, 803–1061 (2010).
Zhao, J. et al. Structural and magnetic phase diagram of CeFeAsO1− xFx and its relation to high-temperature superconductivity. Nature Materials 7, 953–959 (2008).
Garbarino, G. et al. Direct observation of the influence of the As-Fe-As angle on the Tc of superconducting SmFeAsO1−xFx . Phys. Rev. B 84, 024510 (2011).
Kudo, K. et al. Superconducting transition temperatures of up to 47 K from simultaneous rare earth element and antimony doping of 112-type CaFeAs2 . J. Phys. Soc. Jpn. 83, 093705 (2014).
Bao, J. K. et al. Cluster spin-glass ground state in quasi-one-dimensional KCr3As3 . Phys. Rev. B 91, 180404(R) (2015).
Tang, Z. T. et al. Synthesis, crystal structure and physical properties of quasi-one-dimensional ACr3As3 (A = Rb, Cs). Science China Materials 58, 543 (2015).
Kuroki, K., Usui, H., Onari, S., Arita, R. & Aoki, H. Pnictogen height as a possible switch between high-Tc nodeless and low-Tc nodal pairings in the iron-based superconductors. Phys. Rev. B 79, 224511 (2009).
Mizuguchi, Y. et al. Anion height dependence of Tc for the Fe-based superconductor. Supercond. Sci. Technol. 23, 054013 (2010).
Bao, W. et al. Tunable (δπ, δπ)-type antiferromagnetic order in α-Fe (Te, Se) superconductors. Phys. Rev. Lett. 102, 247001 (2009).
Takahashi, H. et al. Superconductivity at 43 K in an iron-based layered compound LaO1−xFxFeAs. Nature 453, 376–378 (2008).
Petrova, A. E., Sidorov, V. A. & Stishov, S. M. High-pressure helium gas apparatus and hydrostatic toroid cell for low-temperatures applications. Physica B 359–361, 1463–1465 (2005).
Eiling, A. & Schilling, J. S. Pressure and temperature dependence of electrical resistivity of Pb and Sn from 1–300 K and 0–10 GPa-use as continuous resistive pressure monitor accurate over wide temperature range; superconductivity under pressure in Pb, Sn, and In. J. Phys. F: Metal Phys. 11, 623–39 (1981).
Mao, H. K., Xu, J. & Bell, P. M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions. J. Geophys. Res. 91, 4673–4676 (1986).
Izumi, F. et al. MEM-based structure-refinement system REMEDY and its applications. Mater. Sci. Forum 378–381, 59–64 (2001).
Izumi, F. & Ikeda, T. A rietveld-analysis program RIETAN-98 and its applications to zeolites. Mater. Sci. Forum 321–324, 198–205 (2000).
Izumi, F. The Rietveld Method (ed. Young, R. A. ) (Oxford University Press, 1995).
Momma, K., Ikeda, T., Belik, A. A. & Izumi, F. Dysnomia, a computer program for maximum-entropy method (MEM) analysis and its performance in the MEM-based pattern fitting. Powder Diffr. 28, 184–193 (2013).
Momma, K. & Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
Acknowledgements
The work was supported by the NSF of China (Grants Nos 91321207, 11427805, U1532267and 11404384), the Strategic Priority Research Program (B) of the Chinese Academy of Sciences (Grant No. XDB07020300), Projects from Ministry of Science and Technology (Grant No. 2016YFA0300300) and the Russian Foundation for Basic Research (Grant No. 15-02-02040).
Author information
Authors and Affiliations
Contributions
Z.W., V.A.S. and L.S. performed high-pressure ac susceptibility measurements. Z.W., W.Y., J.G. Y.Z.Z., S.Z., K.Y., L.Z., S.J., A.G.L. and L.S. did high pressure x-ray diffraction measurements. Z.W., W.Y., Q.W., X.X.W., J.P.H. and L.S. did analysis for the x-ray diffraction results. J.K.B., Z.T., H.L., Y.G.S. and G.H.C. grew the single crystal samples. L.S., Q.W., J.P.H., Z.W., W.Y. and Z.X.Z. wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Wang, Z., Yi, W., Wu, Q. et al. Correlation between superconductivity and bond angle of CrAs chain in non-centrosymmetric compounds A2Cr3As3 (A = K, Rb). Sci Rep 6, 37878 (2016). https://doi.org/10.1038/srep37878
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep37878
This article is cited by
-
Electronic Structures of Newly Discovered Quasi-One-Dimensional Superconductors A2Mo3As3 (A=K,Rb,Cs)
Journal of Superconductivity and Novel Magnetism (2019)
-
Local Noncentrosymmetric Structure of Bi2Sr2CaCu2O8+y by X-ray Magnetic Circular Dichroism at Cu K-Edge XANES
Journal of Superconductivity and Novel Magnetism (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.