Abstract
X-ray induced photoemission yield contains structural information complementary to that provided by X-ray Fresnel reflectivity, which presents an advantage to a wide variety of surface studies if this information is made easily accessible. Photoemission in materials research is commonly acknowledged as a method with a probing depth limited by the escape depth of the photoelectrons. Here we show that the integral hard-X-ray-induced photoemission yield is modulated by the Fresnel reflectivity of a multilayer structure and carries structural information that extends well beyond the photoelectron escape depth. A simple electric self-detection of the integral photoemission yield and Fourier data analysis permit extraction of thicknesses of individual layers. The approach does not require detection of the reflected radiation and can be considered as a framework for non-invasive evaluation of buried layers with hard X-rays under grazing incidence.
Similar content being viewed by others
Introduction
One of the primary difficulties in applications of small-angle X-ray scattering, as one of the dominant methods to study surface morphology is the separation of the measured weak scattered intensity from the strong primary X-ray beam. This problem becomes especially challenging for very hard X-rays with photon energies  10 keV, where the most informative regime of total external reflection is achieved at incidence angles of substantially less than one degree. However, measurement of the reflected radiation is not restrictive to other means of probing the surface morphology in the same experimental conditions. Surface structure of solids can be studied with X-rays using grazing incidence X-ray photoemission spectroscopy (GIXPS) with angles of incidence in the vicinity of the critical angle for total external reflection. GIXPS was established by Henke1 as a method enabling determination of material constants and surface characterization. Further developments were performed2 including generalization to multilayer structures3 followed by experimental effort4,5. The studies were mostly concentrated in the soft X-ray domain (photon energies ≲ 5 keV) for applications in surface science. In spite of prior developments, applications of hard X-ray GIXPS remain limited to date6,7,8. Apart from the regime of grazing incidence hard X-ray photoemission spectroscopy has been successfully used to probe electronic properties of materials at depths consistent with the bulk environment (e.g., refs 9, 10, 11). Probing depths of about 100 Å have been demonstrated12.
10 keV, where the most informative regime of total external reflection is achieved at incidence angles of substantially less than one degree. However, measurement of the reflected radiation is not restrictive to other means of probing the surface morphology in the same experimental conditions. Surface structure of solids can be studied with X-rays using grazing incidence X-ray photoemission spectroscopy (GIXPS) with angles of incidence in the vicinity of the critical angle for total external reflection. GIXPS was established by Henke1 as a method enabling determination of material constants and surface characterization. Further developments were performed2 including generalization to multilayer structures3 followed by experimental effort4,5. The studies were mostly concentrated in the soft X-ray domain (photon energies ≲ 5 keV) for applications in surface science. In spite of prior developments, applications of hard X-ray GIXPS remain limited to date6,7,8. Apart from the regime of grazing incidence hard X-ray photoemission spectroscopy has been successfully used to probe electronic properties of materials at depths consistent with the bulk environment (e.g., refs 9, 10, 11). Probing depths of about 100 Å have been demonstrated12.
Contrary to studies of electronic structure resolving energies of photoelectrons is not essential for probing structural morphology and composition of a multilayer. A substantial simplification of a typical X-ray photoemission spectroscopy setup can be accomplished using self-detection of integral electric charge generated in the exterior of the studied object. This self-detection approach has been used in X-ray absorption spectroscopy in the hard X-ray regime (e.g., refs 13, 14, 15). For hard X-rays the detection technique can take advantage of negligible X-ray absorption in a light gas environment such as helium16,17. Instead, helium is subject to efficient ionization by fast photoelectrons escaping the object, which provides enhancement in the quantum detection yield. The same approach is used in conversion electron Mössbauer spectroscopy (e.g., ref. 18). Self-detection of hard-X-ray induced photoelectron yield in the grazing incidence geometry was used recently to study an X-ray mirror enclosed in a flowing helium gas19. It was shown that the measured integral photoelectron yield as a function of the incidence angle contains structural information i.e., Kiessig fringes, which originate from the layered structure of the mirror.
In this work we show that the structural information extracted from the integral grazing-incidence yield photoemission curves is not limited by the escape depth of photoelectrons but rather is limited by the penetration depth of the X-ray wave. A bi-layer Pt-Cr system on a Si substrate was studied with a deeply buried Cr layer (116.5-Å-thick layer of Cr under 725-Å-thick layer of Pt). Detection of the layered structure using Fourier analysis of the integral photoemission yield is demonstrated at several different photon energies of the incident hard X-rays where the effective photoelectron escape depth is substantially smaller than the depth of the buried layer.
Results and Discussion
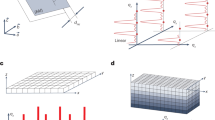
The energy flow through a multilayer system (Fig. 1) and thus the number of generated photoelectrons is proportional to the fraction of energy attenuated by the system, A = 1 − R − T, where R is the net reflectivity of the system and T is the net transmissivity. If the sample is thick such that the fraction of the transmitted X-rays is negligible, then A ≈ 1 − R represents Fresnel transmissivity of the entrance interface. Attentuation of X-rays at depth z within a layer of material having a thickness dz is generally described by the difference between the incoming and outgoing mean energy flow. The energy flow through the layer is represented by the real part of projection Sz(Q, z) of the Poynting vector as a function of the wavevector transfer Q = 2 k sin α, where k is the absolute value of the wavevector of the incident wave and α is the glancing angle of incidence. The normalized total X-ray attenuation per unit depth dz is
Grazing incidence geometry illustrating the incident, the transmitted and the reflected waves.
The energy flow through the layered structure generates ionization events due to X-ray photoabsorption. The escaping fast photoelectons (light blue) ionize the surrounding gas while the low-energy secondary photoelectrons (gray) do not participate in this ionization process. While the ionizing photoelectrons may escape only from a limited depth in the top layer the integral photoelectron yield is affected by the total energy flow in the multilayer and thus is sensitive to presence of buried layers.

where  is the projection of the Poynting vector of the incident wave. The dependence on the photon energy EX of the incident wave is omitted here for clarity.
is the projection of the Poynting vector of the incident wave. The dependence on the photon energy EX of the incident wave is omitted here for clarity.
For an infinitely thick mirror the penetration depth of the wave transmitted through the entrance interface is given by

where

is the wavevector transfer in the mirror material with an index of refraction n = 1 − δ + iβ. It can be shown that for the thick mirror

where T(Q) = 1 − R(Q) is the Fresnel transmissivity. If the thickness of the top layer of a multilayer X-ray mirror is such that the transmitted wave is preferentially attenuated in this layer the energy flow can be approximated with Eq. 4.
Generation of charge carriers above the surface of the mirror is initiated with the escape of photoelectrons. An exponential factor exp[−z/L] (where L is the effective photoelectron escape depth) can be used20,21,22,23 to model propagation of photoelectrons towards the surface of the mirror prior to escape. Taking this factor into account, integration of Eq. 4 results in the following expression for the integral electron quantum yield (yield normalized by the incident photon flux)19.

where εq is the charge collection efficiency, nq is the charge amplification factor and Ge is a proportionality factor, which represents a correction for photoelectron energy conversion. Strictly speaking, only a fraction of the attenuated intensity of the X-rays results in generation of photoelectrons. This photon-energy-dependent fraction is ascribed to Ge to avoid introduction of an additional factor in Eq. 5.
If the X-ray mirror is enclosed in a flow chamber containing light gas (e.g., He) gas impact ionization events produced by the secondary photoelectrons can be neglected (Fig. 1) since the energy required to produce one ion pair is  24 while the energies of the secondary electrons do not exceed ≈20 eV25. In addition, absorption cross section for hard X-rays in He is negligible compared to the ionization cross section by photoelectron impact e.g., ref. 26. Thus, the electric carriers generated in the gas flow chamber originate from the photoelectric response of the mirror material. It is convenient to ascribe the number of charge carriers nq generated by a single photoelectron in the gas flow chamber to the ratio of the maximum photoelectron energy
24 while the energies of the secondary electrons do not exceed ≈20 eV25. In addition, absorption cross section for hard X-rays in He is negligible compared to the ionization cross section by photoelectron impact e.g., ref. 26. Thus, the electric carriers generated in the gas flow chamber originate from the photoelectric response of the mirror material. It is convenient to ascribe the number of charge carriers nq generated by a single photoelectron in the gas flow chamber to the ratio of the maximum photoelectron energy  and the ion pair production energy Wg, nq = 2EX/Wg.
and the ion pair production energy Wg, nq = 2EX/Wg.
Remarkably, the integral electron yield Eq. 5 is represented by the photon-electron attenuation factor L/(Λ(Q) + L) modulated by the Fresnel transmissivity. Precise derivation of the photon-electron attenuation factor for any given material requires modeling of the photoemission processes from various atomic sub-shells and integration of the resulting photoemission cross-sections using the geometry of the photoemission detector. Such rigorous approach could be based on the existing theoretical developments in X-ray photoemission spectroscopy pertaining to X-ray optical effects27. It should be noted that the photon-electron attenuation factor is a slow varying function of Q (or the angle of incidence α). Thus, subtraction of a smooth function, which agrees with the overall shape of the experimental curve should isolate the modulating signal, which contains Kiessig fringes. Structural information can be extracted from the result of the subtraction using Fourier transform similarly to Fourier analysis of the interference structure in X-ray specular reflection28. This strategy is illustrated below applied to a bi-layer X-ray mirror.
Fresnel reflection coefficients of a multilayer system are described by the Parratt’s recursive relation29,30,31:

In our notation Δi is the thickness of layer “i and rij is the reflection coefficient of the interface between layers “i” and “j”

where zero interface roughness is assumed.
We note that any  above the largest critical angle corresponding to the layer with the greatest refractive decrement δ. In this approximation the net Fresnel reflection coefficient of a bi-layer (Fig. 1) is given by
above the largest critical angle corresponding to the layer with the greatest refractive decrement δ. In this approximation the net Fresnel reflection coefficient of a bi-layer (Fig. 1) is given by

The Fresnel transmissivity is given by

where T01 = 1 − |r01|2 is the transmissivity of entrance interface of the thick mirror, the symbol “*” denotes complex conjugation and “c.c.” denotes conjugated components with the oscillating exponential factors. The reflection coefficients rij are non-oscillating functions of the layer thicknesses (i.e., do not contain Kiessig fringes)28. If  substantial attenuation of the transmitted wave occurs in the top layer (i.e., the second layer is deeply buried). Thus, according to Eq. 9 the Fresnel transmissivity of a bi-layer system will differ from that of the thick mirror by components oscillating with frequencies Δ1, Δ2 and the sum frequency Δ1 + Δ2. For the purpose of Fourier analysis in the (Re(Qi), Δ)-space above the greatest critical angle one can assume Re(Q2) ≈ Re(Q1). Generalization of this analysis to the case of arbitrary number of layers is straightforward (see Supplementary Material).
substantial attenuation of the transmitted wave occurs in the top layer (i.e., the second layer is deeply buried). Thus, according to Eq. 9 the Fresnel transmissivity of a bi-layer system will differ from that of the thick mirror by components oscillating with frequencies Δ1, Δ2 and the sum frequency Δ1 + Δ2. For the purpose of Fourier analysis in the (Re(Qi), Δ)-space above the greatest critical angle one can assume Re(Q2) ≈ Re(Q1). Generalization of this analysis to the case of arbitrary number of layers is straightforward (see Supplementary Material).
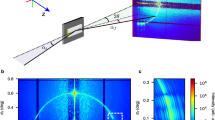
To address the problem experimentally integral photoemission yield and X-ray reflectivity of a bi-layer Pt-Cr X-ray mirror were measured simultaneously at several different photon energies in the range 8–23 keV. Prior to the analysis of integral electron yield the mirror was fully characterized using X-ray reflectivity (XRR), a method commonly used for structural characterization of surfaces29. As determined by XRR the thickness of the top Pt layer was Δ1 = 725.2 Å and that of the buried Cr layer was Δ2 = 116.5 Å. The measured reflectivities and XRR fitting curves are shown in Fig. 2 (see Methods for details). The Pt-Cr interface roughness was found to be 7.5 Å, while the Cr-Si interface roughness was 4.5 Å. Although the multilayer system used in the experiment was an X-ray optical element prepared under the controlled environment, we note that similar interface qualities are often found in non-X-ray optical metallic multilayer systems such as those used in nuclear reactor coatings32,33.
Specular X-ray reflectivity (black squares) from the Pt/Cr bilayer deposited on the Si substrate, together with the fitting curves (solid red lines).
The error bars indicate ±1 standard deviation. The X-ray energy at which the corresponding data were taken is indicated to the right. The curves are offset by one order of magnitude for clarity.
In derivation of Eq. 5 we used the fact that slow secondary photoelectrons have insufficient energy to ionize the gas and the assumption that the escaping fast photoelectrons have energies comparable to the energy of incident photons. Because the escape depth is a monotonically increasing function of the electron energy the effective escape depth obtained by fitting experimental data to Eq. 5 is the upper estimate for actual escape depths of photoelectrons originated from different atomic subshells. Thus, the effective escape depth limits the probing depth of electronic structure in photoemission experiments. However, probing the surface structure in the same experiments beyond this limit is possible.
Figure 3 illustrates the strategy used to extract thicknesses of individual layers from the integral photoemission yield curve. In the first step the curves collected at different photon energies were renormalized in the units of quantum yield (electric current divided by the incident flux and unit electric charge) and fit using Eq. 5. The effective photoelectron escape depths were found to be L ≈ 200–400 Å with greater values obtained at higher photon energies (see Table S1 for the summary of the parameters extracted from the fits). Figure 3(a) shows the resulting experimental curve (blue circles) and the fit (solid green line) for the photon energy EX = 10 keV. The Kiessig fringes were clearly observed (magnified region shown in the inset of Fig. 3(a)). In the next step, the fit was subtracted from the experimental data to isolate the differential yield containing the structural information. The differential yield ΔY (Q1) is shown in Fig. 3(b) as a function of wavevector transfer Re(Q1) in the Pt layer. We note that the relative strength of the structural oscillations is ≈10−2 as compared to the maximum yield. If these were originating only from the photoelectrons escaping from the depth as large as the thickness of the Pt layer (725.2 Å) with the effective photoelectron attenuation depth ≈270 Å (Supplementary Material) one would expect their relative strength to be about an order of magnitude smaller. This is because the intensity of the X-ray wave exciting the photoelectrons is limited by the penetration depth (Eq. 2). The observed relative strength is consistent with the effect caused by the penetration depth only (Λ ≲ 200  at Q1 ≈ 0.1 Å−1 where strong oscillations are observed), which indicates that the photoemission yield as a structural probe is not limited by the escape depth of the photoelectrons.
at Q1 ≈ 0.1 Å−1 where strong oscillations are observed), which indicates that the photoemission yield as a structural probe is not limited by the escape depth of the photoelectrons.
Integral photoelectron yield and Fourier power spectra showing the structure of the Pt-Cr-Si bi-layer X-ray mirror.
(a) Measured integral photoelectron yield as a function of the wavevector transfer Q of the incident wave at 10 keV (circles) and fit to Eq. 5 corresponding to photoelectron yield of a thick Pt mirror (green solid line). The inset shows magnified region above the critical angle where the Kiessig fringes due to the layered structure of the mirror are clearly observed. (b) Differential photoelectron yield (circles, Y-error bars and solid line) obtained as the difference between the experimental data and the fit in (a). The differential yield is plotted as a function of the real part of Q1, the wavevector transfer inside the Pt layer. (c) Forier power spectrum (circles, solid line) of the differential yield (b) showing peaks corresponding to thicknesses of individual layers (Δ1 and Δ2 and their sum. (d) Fourier power spectra (circles, solid lines) obtained at different photon energies (shifted for clarity).
The power spectrum of a Fourier transform applied to ΔY (Q1) is shown in Fig. 3(c). Peaks in the spectrum correspond to thicknesses of the individual layers with precision on the order of spectral resolution 2π/ΔQ1  10–18 Å defined by the available range of the wavevector transfer ΔQ1. The low-Δ region of the spectrum with peak corresponding to the buried Cr layer (116.5 Å) could be contaminated by non-ideal subtraction procedure using the baseline, which includes the approximated photon-electron attenuation factor and the transmissivity of the thick mirror. Thus, evaluation of the thickness of the buried layer from the position of this peak alone can raise doubts. However, the appearance of the peak corresponding to the sum frequency Δ1 + Δ2 in the same spectrum confirms the presence of the Cr layer and its thickness. Also, the relatively featureless high-Δ region of the spectrum validates the approximation on the smallness of |rij| given by Eq. 8.
10–18 Å defined by the available range of the wavevector transfer ΔQ1. The low-Δ region of the spectrum with peak corresponding to the buried Cr layer (116.5 Å) could be contaminated by non-ideal subtraction procedure using the baseline, which includes the approximated photon-electron attenuation factor and the transmissivity of the thick mirror. Thus, evaluation of the thickness of the buried layer from the position of this peak alone can raise doubts. However, the appearance of the peak corresponding to the sum frequency Δ1 + Δ2 in the same spectrum confirms the presence of the Cr layer and its thickness. Also, the relatively featureless high-Δ region of the spectrum validates the approximation on the smallness of |rij| given by Eq. 8.
Figure 3(d) shows power spectra of the differential yield of the bi-layer mirror at different photon energies. The peaks corresponding to individual thicknesses Δ1 and Δ2 as well as the sum Δ1 + Δ2 are clearly observed at photon energies 10 keV and 11 keV where Kiessig fringes are most intense. At some other photon energies (e.g., 13.5 keV and 15 keV) the noise level in the differential yield exceeds the weights of the spectral components. However, at higher photon energies (18 keV and 23 keV) reliable spectral detection of the thicknesses is still possible. Overall, the magnitude of the spectral components at various photon energies is consistent with the intensity of Kiessig fringes observed in XRR (Fig. 2), which is governed by the energy-dependent absorption losses in the Pt layer. At 10–11 keV just below the energy region, which includes Pt L-absorption edges (L3 at 11.56 keV, L2 at 13.27 keV and L1 at 13.88 keV) the imaginary parts of the refractive index (β) for Pt and Cr become comparable resulting in the increased intensity of the fringes. At the intermediate photon energies (12 keV–15 keV) β for Pt increases substantially in comparison to that of Cr. Finally, at higher photon energies (18 keV, 23 keV) the absorption losses for Pt become sufficiently small and the intensity of the fringes again increases. However, the absorption contrast between Pt and Cr remains substantial which explains reduction in the intensity of spectral peaks at Δ2 and Δ1 + Δ2.
Conclusions
In summary, our findings demonstrate that structure of buried layers can be studied with hard X-rays, yet, without detection of the reflected radiation. Instead, integral photoelectron yield is detected using simple voltage-bias-driven collection of generated electric charges above the surface of the studied material. It should be mentioned that the approach is rather general and is not limited to the case where the top layer represents a conductive material. Indeed, self-detection of X-ray standing wave-effects have been observed on non-conductive materials such as diamond (e.g., ref. 34). The approach could be used to advance the field of non-destructive evaluation where unique field applications can become feasible. In particular, it can be useful for quantitative evaluation of surfaces in enclosed geometries where implementation of the conventional θ − 2θ XRR arrangement is not possible. Determination of the scattering vector (or the absolute angular scale) is essential in XRR experiments as well as in our study. It is often performed using the position of the reflected beam in the θ − 2θ arrangement. However, alternative methods can be used. If optical constants of one of the layers in the material are known the scattering vector can be defined via fitting the experimental integral photoelectron yield curve to Eq. 5 using a variable angular offset as it was demonstrated earlier19. The precision of this procedure was also confirmed in the present study by the resulting small fitted errors in the angular offsets (see Table S1). Also, with integral photoelectron yield the use of very hard X-rays at grazing incidence for studies of surface structure becomes feasible since contrary to XRR no effort is required to isolate the reflected radiation from the incident X-rays. Thus, the approach is not only complementary to XRR but it could become indispensable for non-destructive evaluation of surfaces in tribology applications, as well as concealed coatings in nuclear reactors, hydrocarbon transport systems, semiconductor circuits and other systems with buried layers and interfaces.
Materials and Methods
Experimental
An X-ray mirror was prepared by deposition of a Pt film with thickness  700 Å on top of a ≈ 100-Å-thick layer of Cr on a polished Si substrate. The length of the mirror was 80 mm and the width was 20 mm. The mirror was placed on a non-conductive surface and contained in a helium flow chamber having an entrance and exit windows made of Kapton® film. The metallic working surface of the mirror served as the first electrode while a separate second grounded electrode was placed inside the chamber above the mirror at a distance of about 20 mm. The experiment was performed at 1-BM beamline of the Advanced Photon Source. The X-ray beam incident on the mirror was delivered by a Si (111) double-crystal monochromator (DCM). The DCM was detuned to suppress high-order Si Bragg reflections at high photon energies. The electric current between the electrodes in the flow chamber was measured using a source meter with applied bias voltages of ±200 V. The observed maximum electric currents (at the photoemission peak) were
700 Å on top of a ≈ 100-Å-thick layer of Cr on a polished Si substrate. The length of the mirror was 80 mm and the width was 20 mm. The mirror was placed on a non-conductive surface and contained in a helium flow chamber having an entrance and exit windows made of Kapton® film. The metallic working surface of the mirror served as the first electrode while a separate second grounded electrode was placed inside the chamber above the mirror at a distance of about 20 mm. The experiment was performed at 1-BM beamline of the Advanced Photon Source. The X-ray beam incident on the mirror was delivered by a Si (111) double-crystal monochromator (DCM). The DCM was detuned to suppress high-order Si Bragg reflections at high photon energies. The electric current between the electrodes in the flow chamber was measured using a source meter with applied bias voltages of ±200 V. The observed maximum electric currents (at the photoemission peak) were  10–80 nA with greater values at higher photon energies. Electric current in the absence of X-rays (i.e., dark current) was ≈100 pA. The root mean square fluctuations in the measured signal were about 20 pA. A calibrated solid state detector was placed behind the flow chamber to measure the reflected X-ray flux (mirror in the beam) and the incident X-ray flux (mirror out of the beam). The size of the incident beam was set to 0.1 × 3.0 mm2 (vertical × horizontal) using X-ray slits placed upstream of the mirror chamber. The incident beam was centered on the surface of the mirror. Simultaneous measurement of the reflectivity and the electric current were performed while scanning the mirror’s grazing angle α at different photon energies selected by the double-crystal monochromator. Prior to each scan the incident photon flux was measured using the solid state detector. The measured values were in the range 7 × 108–2 × 109 photons/s. The experimental setup is shown in Fig. 4(a).
10–80 nA with greater values at higher photon energies. Electric current in the absence of X-rays (i.e., dark current) was ≈100 pA. The root mean square fluctuations in the measured signal were about 20 pA. A calibrated solid state detector was placed behind the flow chamber to measure the reflected X-ray flux (mirror in the beam) and the incident X-ray flux (mirror out of the beam). The size of the incident beam was set to 0.1 × 3.0 mm2 (vertical × horizontal) using X-ray slits placed upstream of the mirror chamber. The incident beam was centered on the surface of the mirror. Simultaneous measurement of the reflectivity and the electric current were performed while scanning the mirror’s grazing angle α at different photon energies selected by the double-crystal monochromator. Prior to each scan the incident photon flux was measured using the solid state detector. The measured values were in the range 7 × 108–2 × 109 photons/s. The experimental setup is shown in Fig. 4(a).
Prior to collection of angular curves an IV curve of the system was measured at the photoemission peak angle for each photon energy. The resulting IV curves are shown in Fig. 4(b). In all cases saturation of the electric current and thus linear ionization-chamber-like response (full charge collection  ) was achieved at sufficiently large negative potentials (−200 V) applied to the mirror surface. The absence of saturation at the positive potential (+200 V) suggests that the potential is insufficient to recapture all the electrons in the system. We note that in the case of Pd mirror studied earlier19 full charge collection was observed for both positive and negative potentials. Detailed explanation of this phenomenon requires consideration of energy spectra of the emitted photoelectrons and their energy transfer to He atoms via collision processes. For the purpose of linearity of detection of the integral photoelectron yield it was sufficient to ascertain the saturation at −200 V in the present case.
) was achieved at sufficiently large negative potentials (−200 V) applied to the mirror surface. The absence of saturation at the positive potential (+200 V) suggests that the potential is insufficient to recapture all the electrons in the system. We note that in the case of Pd mirror studied earlier19 full charge collection was observed for both positive and negative potentials. Detailed explanation of this phenomenon requires consideration of energy spectra of the emitted photoelectrons and their energy transfer to He atoms via collision processes. For the purpose of linearity of detection of the integral photoelectron yield it was sufficient to ascertain the saturation at −200 V in the present case.
Structural analysis using XRR
XRR measures the intensity of the specularly reflected beam as a function of the wavevector transfer Q to extract the scattering length density (SLD) profile of the sample. SLD yields the information about the chemical composition of each layer, its thickness, physical density and interfacial roughness. One of the main disadvantages of XRR is that spatial separation of the incident and the specularly reflected radiation becomes problematic in very grazing incidence  at high photon energies
at high photon energies  . Reliable detection of the specularly reflected radiation requires θ − 2θ geometry and a large dynamic range of the radiation detector. These factors restrict the use of XRR to an X-ray analytical laboratory or a specialized X-ray source facility. Thus, despite the high penetrating power of hard X-rays, surfaces studies using XRR are limited to model systems or surface sections destructively extracted from real systems. In our case of a model system (bi-layer X-ray mirror) XRR was fully applicable. For the XRR modelling we used dynamic Parratt’s formalism29 combined with Nevot–Croce interface roughness and genetic fitting algorithm using the MOTOFIT software35. Literature SLD values for the Si substrate, Cr and Pt layers were used for modelling and the individual thicknesses of Pt (705.2 Å) and Cr (116.5 Å) layers, as well as the interfacial roughness at Pt-Cr (σ12 = 7.5 Å) and Cr-Si (σ23 = 4.5 Å) interfaces, were kept the same for all energies. In this experiment, lateral projection of the coherence length lc (a few tens of microns) of the radiation is much smaller than the sample surface along the beam (80 mm). Therefore, the local surface roughness (within the length lc) from different parts of the sample is averaged incoherently. Such averaging is represented in the model by an additional top layer of 20 Å-thick with SLD
. Reliable detection of the specularly reflected radiation requires θ − 2θ geometry and a large dynamic range of the radiation detector. These factors restrict the use of XRR to an X-ray analytical laboratory or a specialized X-ray source facility. Thus, despite the high penetrating power of hard X-rays, surfaces studies using XRR are limited to model systems or surface sections destructively extracted from real systems. In our case of a model system (bi-layer X-ray mirror) XRR was fully applicable. For the XRR modelling we used dynamic Parratt’s formalism29 combined with Nevot–Croce interface roughness and genetic fitting algorithm using the MOTOFIT software35. Literature SLD values for the Si substrate, Cr and Pt layers were used for modelling and the individual thicknesses of Pt (705.2 Å) and Cr (116.5 Å) layers, as well as the interfacial roughness at Pt-Cr (σ12 = 7.5 Å) and Cr-Si (σ23 = 4.5 Å) interfaces, were kept the same for all energies. In this experiment, lateral projection of the coherence length lc (a few tens of microns) of the radiation is much smaller than the sample surface along the beam (80 mm). Therefore, the local surface roughness (within the length lc) from different parts of the sample is averaged incoherently. Such averaging is represented in the model by an additional top layer of 20 Å-thick with SLD  80–85% of the literature value for Pt. In other words, this top layer can be considered as a long-scale mirror height profile with a peak-to-valley value of 20 Å, consistent with the Pt deposition specification.
80–85% of the literature value for Pt. In other words, this top layer can be considered as a long-scale mirror height profile with a peak-to-valley value of 20 Å, consistent with the Pt deposition specification.
Additional Information
How to cite this article: Stoupin, S. et al. Surface studies of solids using integral X-ray-induced photoemission yield. Sci. Rep. 6, 37440; doi: 10.1038/srep37440 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Change history
15 March 2017
A correction has been published and is appended to both the HTML and PDF versions of this paper. The error has been fixed in the paper.
References
Henke, B. L. Ultrasoft-X-ray reflection, refraction and production of photoelectrons (100–1000-ev region). Phys. Rev. A 6, 94–104 (1972).
Fadley, C. Instrumentation for surface studies: XPS angular distributions. J. Electron Spectrosc. Relat. Phenom. 5, 725–754 (1974).
Chester, M. J. & Jach, T. Grazing-incidence X-ray photoelectron spectroscopy from multilayer media: Oxidized GaAs (100) as a case study. Phys. Rev. B 48, 17262–17270 (1993).
Kawai, J. et al. Total reflection X-ray excited photoelectron spectra of copper phthalocyanine thin layer on Si wafer. Appl. Phys. Lett. 67, 3889–3891 (1995).
Hayashi, K. et al. Photoelectron spectra enhanced by X-ray total reflection and diffraction from periodic multilayer. Appl. Phys. Lett. 68, 1921–1923 (1996).
Fadley, C. S. X-ray photoelectron spectroscopy and diffraction in the hard x-ray regime: Fundamental considerations and future possibilities. Nucl. Instrum. Methods Phys. Res. A 547, 24–41 (2005).
Fadley, C. X-ray photoelectron spectroscopy: Progress and perspectives. J. Electron Spectrosc. Relat. Phenom. 178–179, 2–32 (2010).
Kawai, J. Total reflection X-ray photoelectron spectroscopy: A review. J. Electron Spectrosc. Relat. Phenom. 178–179, 268–272 (2010).
Sekiyama, A. et al. Probing bulk states of correlated electron systems by high-resolution resonance photoemission. Nature 403, 396–398 (2000).
Gray, A. X. et al. Bulk electronic structure of the dilute magnetic semiconductor Ga1−xMnxAs through hard X-ray angle-resolved photoemission. Nat. Mater. 11, 957–962 (2012).
Feng, D.-L. Photoemission spectroscopy: Deep into the bulk. Nat. Mater. 10, 729–730 (2011).
Dallera, C. et al. Looking 100 Å deep into spatially inhomogeneous dilute systems with hard X-ray photoemission. Appl. Phys. Lett. 85, 4532 (2004).
Martens, G., Rabe, P., Schwentner, N. & Werner, A. Exafs in photoelectron yield spectra and optimisation of the photon glancing angle. J. Phys. C: Solid St. Phys. 11, 3125 (1978).
Martens, G., Rabe, P., Tolkiehn, G. & Werner, A. EXAFS in photoelectron yield spectra at K edges of Cu, Ni and Ge. Phys. Stat. Solidi (a) 55, 105–108 (1979).
Erbil, A., Cargill, G. S., III, Frahm, R. & Boehme, R. F. Total-electron-yield current measurements for near-surface extended X-ray-absorption fine structure. Phys. Rev. B 37, 2450–2464 (1988).
Kordesch, M. E. & Hoffman, R. W. Electron-yield extended X-ray absorption fine structure with the use of a gas-flow electron detector. Phys. Rev. B 29, 491–492 (1984).
Guo, T. & denBoer, M. L. Extended X-ray-absorption fine structure: Direct comparison of absorption and electron yield. Phys. Rev. B 31, 6233–6237 (1985).
Jones, W., Thomas, J. M., Thorpe, R. K. & Tricker, M. J. Conversion electron Mössbauer spectroscopy and the study of surface properties and reactions. Applications of Surface Science 1, 388–407 (1978).
Stoupin, S. Self-detection of X-ray Fresnel transmissivity using photoelectron-induced gas ionization. Appl. Phys. Lett. 108, 041101 (2016).
Pepper, S. V. Optical analysis of photoemission. J. Opt. Soc. Am. 108, 805–812 (1970).
Birken, H.-G. et al. Angular dependent photoelectric yield and optical constants of Al between 40 and 600 eV. Nucl. Instrum. Methods Phys. Res. A 253, 166–170 (1986).
Stöhr, J. NEXAFS spectroscopy vol. 25 of Springer Series in Surface Sciences (Springer, Berlin Heidelberg New York, 1992).
Ejima, T. Formulae of total electron yield for multilayers: extention of Pepper’s method. Japn. J. Appl. Phys. 42, 6459 (2003).
Weiss, J. & Bernstein, W. Energy required to produce one ion pair in several noble gases. Phys. Rev. 103, 1253–1253 (1956).
Henke, B. L., Smith, J. A. & Attwood, D. T. 0.1–10-kev X-ray-induced electron emissions from solids—models and secondary electron measurements. J. Appl. Phys. 48, 1852–1866 (1977).
Shah, M. B., Elliott, D. S., McCallion, P. & Gilbody, H. B. Single and double ionisation of helium by electron impact. J. Phys. B: At. Mol. Opt. Phys 21, 2751 (1988).
Yang, S.-H. et al. Making use of X-ray optical effects in photoelectron-, auger electron- and X-ray emission spectroscopies: Total reflection, standing-wave excitation and resonant effects. J. Appl. Phys. 113, 073513 (2013).
Sakurai, K. & Iida, A. Fourier analysis of interference structure in X-ray specular reflection from thin films. Japn. J. Appl. Phys. 31, L113–L115 (1992).
Parratt, L. G. Surface studies of solids by total reflection of X-rays. Phys. Rev. 95, 359–369 (1954).
Hau-Riege, S. P. High-Intensity X-Rays – Interaction with Matter (WILEY-VCH Verlag GmbH&Co. KGaA, Boschstr. 12, 69469, Weinheim, Germany, 2011).
Windt, D. L. IMD–software for modeling the optical properties of multilayer films. Computers in Physics 12, 360–370 (1998).
Zhernenkov, M. et al. Trapping of implanted He at Cu/Nb interfaces measured by neutron reflectometry. Appl. Phys. Lett. 98, 241913 (2011).
Zhernenkov, M. et al. Design of radiation resistant metallic multilayers for advanced nuclear systems. Appl. Phys. Lett. 104, 241906 (2014).
Stoupin, S., Baryshev, S. V. & Antipov, S. P. Flux monitoring by X-ray diffracting crystals under ambient air conditions. Proc. SPIE - Int. Soc. Opt. Eng. 9207, doi: 10.1117/12.2062495 (2014).
Nelson, A. Co-refinement of multiple-contrast neutron/X-ray reflectivity data using MOTOFIT. J. Appl. Cryst. 39, 273–276 (2006).
Acknowledgements
K. Lang is acknowledged for technical support. Use of the Advanced Photon Source was supported by the US. Department of Energy, Office of Science, under Contract No. DE-AC02-06CH11357. The work at the National Synchrotron Light Source-II, Brookhaven National Laboratory, was supported by the US. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-SC0012704.
Author information
Authors and Affiliations
Contributions
S.S. and M.Z. performed the experiments, analyzed the data and wrote the paper. B.S. designed and fabricated the X-ray mirror.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Stoupin, S., Zhernenkov, M. & Shi, B. Surface studies of solids using integral X-ray-induced photoemission yield. Sci Rep 6, 37440 (2016). https://doi.org/10.1038/srep37440
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep37440
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.