Abstract
We argue that the alignment of Lyapunov vectors provides a quantitative criterion to predict catastrophes, i.e. the imminence of large-amplitude events in chaotic time-series of observables generated by sets of ordinary differential equations. Explicit predictions are reported for a Rössler oscillator and for a semiconductor laser with optoelectronic feedback.
Similar content being viewed by others
Introduction
The prediction of catastrophic events is arguably one of the most important open problems in physics and in the natural sciences. Catastrophes can be roughly defined as short-duration, large-amplitude events which follow and are followed by relatively long and random intervals of maturation1,2. The great challenge is, of course, to anticipate the duration of the random quiescent intervals and thus to predict impinging undesirable events such as earthquakes, tsunamis, rogue waves, market crashes, political crisis, etc. Considerable work was done in the last years to understand the mechanisms behind the emergence of large-amplitude pulses3. An idea of the intense activity concerning outliers in several distinct lasers, in nanophotonic devices and media, in excitable systems, and in other key applications may be obtained by perusing a small selection of representative papers published in the last two years4,5,6,7,8,9,10,11,12,13,14,15.
Our aim here is to introduce a quantitative indicator capable of anticipating the imminence of large-amplitude events in chaotic time series. As far as we know, there exists hitherto no quantitative criterion for predicting such large-amplitude events. As defined below, the quantitative measure proposed here is based on the so-called Lyapunov vectors (LVs)16,17,18,19,20,21, namely on useful vectors which provide a step-by-step big-data record of what exactly happens with the angles between stable and unstable manifolds during the whole evolution of a given dynamical process. As shown below explicitly, we find the onset of large peaks in a physical variable of interest to be related to the alignment of LVs along the flow direction. Therefore, since Lyapunov vector alignment precedes large peaks, it can be used to predict the later. Our findings are empirical observations based on numerical computations and, therefore, the conclusions presented here are simply conjectures.
Lyapunov vectors are attracting growing interest nowadays and providing new insight about the dynamics of complex systems. For instance, LVs deliver not only the familiar spectrum of Lyapunov exponents, but also angles between stable and unstable invariant manifolds for every point along the temporal evolution. LVs are obtained by integrating the equations of motion forward and backward in time along the same trajectory according to algorithms described in the literature16,17,18,19,20,21. So far, LVs have been fruitfully applied to rather distinct situations, from turbulence governed by partial differential equations to the evolution of interacting neutrino gas16,22,23,24, from properties of thermal reservoirs to cluster synchronization in scale-free networks21,25, from traffic of vehicles to ocean-atmosphere modeling18,26, and from self-similarity and angle-enhanced bifurcation diagrams to dissipative holes in conservative tori20,27.
Before proceeding, we mention that much work has been done recently concerning phenomena called extreme events independently of whether they are governed by partial differential equations or not. In works related to extreme events and in particular in the field of laser dynamics, there is no consensus on what would be a good definition of an extreme event. Some refer to a definition taken from hydrodynamics and consider as extreme a threshold for the amplitude of a pulse at twice the abnormality index. Others consider that large-amplitude pulse means that the amplitude is larger than the mean-amplitude of the pulses plus a few values of the standard deviation. And there are also papers where one looks to the deviation of the statistics of the pulse amplitude as a parameter varies. For a review, see the collection of review papers presented by Akhmediev et al.3. Here, however, we are not concerned with extreme events but, instead, with large-amplitude pulses commonly observed in experiments and analysed using small sets of ordinary differential equations.
Results
As described in Methods, the angles between LVs are calculated from the expression20

Our illustrative examples below involve chaotic dynamics and three Lyapunov exponents  ordered such that λ1 > 0, λ2 = 0 and λ3 < 0. One has the following situations for the angles between LVs: (i) θ13 is the angle between the unstable and stable manifolds, (ii) θ23 is the angle between the stable manifold and the flow direction, (iii) θ12 is the angle between the unstable manifold and the flow direction.
ordered such that λ1 > 0, λ2 = 0 and λ3 < 0. One has the following situations for the angles between LVs: (i) θ13 is the angle between the unstable and stable manifolds, (ii) θ23 is the angle between the stable manifold and the flow direction, (iii) θ12 is the angle between the unstable manifold and the flow direction.
Catastrophes in Rössler’s oscillator
While studying flows in three dimensions, Rössler was interested in reinjection mechanism where a trajectory, after having a slow motion in one part of a manifold in the phase space, jumps through large excursions to another branch of the manifold. A prototype set of equations with the minimum ingredients for producing sequences of such large excursions is28:

Here, (x, y, z) are real variables evolving continuously as a function of time, ( ) are the corresponding velocities, and (a, b, c) are real parameters controlling the oscillator. These equations give rise to oscillations of x and y which are amplified for a > 0 and result in a spiraling-out motion. Such outbound oscillations are coupled to the z variable in a nonlinear way which induces the reinjection back to the center region, with the cycle of spiraling-out and reinjection repeating indefinitely.
) are the corresponding velocities, and (a, b, c) are real parameters controlling the oscillator. These equations give rise to oscillations of x and y which are amplified for a > 0 and result in a spiraling-out motion. Such outbound oscillations are coupled to the z variable in a nonlinear way which induces the reinjection back to the center region, with the cycle of spiraling-out and reinjection repeating indefinitely.
Figure 1 displays a typical chaotic trajectory, obtained for a = 0.38, b = 0.3, and c = 4.82 and initial condition near the unstable fixed point x = y = z = 0. Colors represent the values of the aforementioned angle θ23. Parallel to the xy plane there is spiraling-out motion, represented in green (θ23 ~ π/2), while the reinjection loops are shown in black and red, associated with θ23 approaching either 0 or π, respectively. The attractor in Fig. 1 was obtained solving Eq. (2) numerically with the standard fourth-order Runge-Kutta algorithm and fixed time-step h = 0.05. The first 107 steps were discarded as transient, with LVs computed subsequently for 8 × 105 steps (including forward and backward time motion). The chaotic trajectory shown is of screw type28 with irregular oscillations in amplitude and in reinjection times.
The time-series of the representative trajectory shown in Fig. 1 consists of large pulses along the z-axis (associated with a homoclinic orbit30) and are separated by irregular time intervals during which the trajectory has chaotic oscillations basically confined to the (x, y) plane. The large peaks in the z-axis start just before the trajectory gets reinjected back near the origin (i.e. near to the unstable fixed point x = y = z = 0). Our purpose is to show that using the angle between the LVs it is possible to predict when large peaks in the z-axis occur. From Fig. 1 one sees clearly that  well before the large peaks emerge out of the (x, y) plane.
well before the large peaks emerge out of the (x, y) plane.
Figure 2 illustrates the relation between the LVs and the emergence of large spikes. The black curve shows the temporal evolution of z, the red line displays θ23, and the blue line depicts the variation of the derivative  . For easier visualization, we plot
. For easier visualization, we plot  . In this range, z presents two large peaks (with z > 10, marked P) and two intermediate peaks (with z ~ 5, marked NP). The blue curve shows that for all four peaks the quantity
. In this range, z presents two large peaks (with z > 10, marked P) and two intermediate peaks (with z ~ 5, marked NP). The blue curve shows that for all four peaks the quantity  has a local minimum slightly before the peaks. The beginning of two such minima is indicated by vertical green lines. The key here is to observe that before large peaks in z, fast variations of
has a local minimum slightly before the peaks. The beginning of two such minima is indicated by vertical green lines. The key here is to observe that before large peaks in z, fast variations of  occur when, in the red curve, θ23 rapidly changes either from π/2 → 0 (leftmost peak) or from π/2 → π (rightmost peak).
occur when, in the red curve, θ23 rapidly changes either from π/2 → 0 (leftmost peak) or from π/2 → π (rightmost peak).
The above observations suggest the interplay of two conditions prior to the occurrence of spikes. First, an alert condition occurs when the presence of a minimum in  signals to an imminent spike but without indication of its amplitude. A pair of alert conditions are indicated by the vertical green lines in Fig. 2 (using
signals to an imminent spike but without indication of its amplitude. A pair of alert conditions are indicated by the vertical green lines in Fig. 2 (using  ). Second, an effective catastrophe condition is detected by inspecting how close θ23 approaches either 0 or π, defined by two suitable thresholds
). Second, an effective catastrophe condition is detected by inspecting how close θ23 approaches either 0 or π, defined by two suitable thresholds  and
and  . This catastrophe condition corresponds to LV alignment condition, i.e. when the stable manifold aligns along the direction of flow thereby providing information concerning the intensity of the imminent spike. The detection of a pair of catastrophes is indicated by vertical magenta lines in Fig. 2 (using
. This catastrophe condition corresponds to LV alignment condition, i.e. when the stable manifold aligns along the direction of flow thereby providing information concerning the intensity of the imminent spike. The detection of a pair of catastrophes is indicated by vertical magenta lines in Fig. 2 (using  and
and  ). Accordingly, peaks labeled P (predicted catastrophes) satisfy both alert and catastrophe conditions, while peaks labeled NP (non-predicted catastrophes) satisfy only the alert condition. Of course, the discrimination between P and NP can be controlled by tuning the aforementioned thresholds.
). Accordingly, peaks labeled P (predicted catastrophes) satisfy both alert and catastrophe conditions, while peaks labeled NP (non-predicted catastrophes) satisfy only the alert condition. Of course, the discrimination between P and NP can be controlled by tuning the aforementioned thresholds.
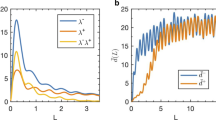
To quantify the relation between the LV alignment condition and the intensity of the spikes, Fig. 3 displays local maxima z > 1 as a function of the θ23 maxima (close to π) and minima (close to 0) for Rössler’s oscillator (Fig. 2). The two vertical red lines mark the thresholds  and
and  . To obtain Fig. 3 we evolved the trajectory for a long time checking when maxima (minima) of θ23 were larger (smaller) than 1.9 (1.2). After this, we computed the maximum (minimum) of θ23 until a peak in z appeared. In other words, we determined how close θ23 approaches 0 (or π) near peaks with z > 1. From Fig. 3 one sees that all peaks with large z values are associated with angles θ23 close to either 0 or π.
. To obtain Fig. 3 we evolved the trajectory for a long time checking when maxima (minima) of θ23 were larger (smaller) than 1.9 (1.2). After this, we computed the maximum (minimum) of θ23 until a peak in z appeared. In other words, we determined how close θ23 approaches 0 (or π) near peaks with z > 1. From Fig. 3 one sees that all peaks with large z values are associated with angles θ23 close to either 0 or π.
To assess the performance of the alignment conditions over extended intervals of time the trajectory was integrated much longer, for t = 5 × 104 time steps. The LV alignment was checked automatically using a pair of threshold values  and
and  . In this way, a total of 3745 peaks were found to obey the alert condition
. In this way, a total of 3745 peaks were found to obey the alert condition  , i.e. peaks which are potentially catastrophes. Of this total, 2372 where indeed found to be P (predicted) catastrophes, namely zmax > 9.11, the value corresponding to the crossing in Fig. 3 of the red lines with the min and max curves. The remaining 1373 spikes were smaller NP (non predicted) events. Spikes in the classes P and NP were separated by imposing numerically the alarm and LV alignment conditions. Thus, all detected spikes were correctly accounted for. In addition, on average we determined alert times to precede spikes by ~2.2 time units, and catastrophe times to precede by ~0.85 time units. Of course, much earlier prediction times are obtained using less stringent values for
, i.e. peaks which are potentially catastrophes. Of this total, 2372 where indeed found to be P (predicted) catastrophes, namely zmax > 9.11, the value corresponding to the crossing in Fig. 3 of the red lines with the min and max curves. The remaining 1373 spikes were smaller NP (non predicted) events. Spikes in the classes P and NP were separated by imposing numerically the alarm and LV alignment conditions. Thus, all detected spikes were correctly accounted for. In addition, on average we determined alert times to precede spikes by ~2.2 time units, and catastrophe times to precede by ~0.85 time units. Of course, much earlier prediction times are obtained using less stringent values for  and
and  . For instance, using
. For instance, using  and
and  the catastrophe prediction time increases to 1.51, almost doubles, on the average. In this case 2944 peaks of type P were detected. We remark that the large interval of integration chosen above was used simply to check that the method was able to detect the imminence of large pulses to get a feeling for the distribution of large events in the model considered. Large integration intervals are by no means needed to predict catastrophes.
the catastrophe prediction time increases to 1.51, almost doubles, on the average. In this case 2944 peaks of type P were detected. We remark that the large interval of integration chosen above was used simply to check that the method was able to detect the imminence of large pulses to get a feeling for the distribution of large events in the model considered. Large integration intervals are by no means needed to predict catastrophes.
Catastrophes in semiconductor laser with optoelectronic feedback
Trajectories for Rössler’s equations are known to be closely related to the presence of Shilnikov homoclinic orbits in the system28,29,30. To check a possible influence of homoclinicity on the prediction times, in the next example we consider a situation where Shilnikov’s theorem does not apply31,32, namely we consider a semiconductor laser with optoelectronic feedback. The aim here is to show that the alignment of LVs is able to predict large peaks also in absence of homoclinicity. In dimensionless units the laser is governed by the equations31,32



Here, the variables x, y, w are proportional to the photon density, the carrier density, and the laser intensity, respectively, while  are corresponding rate of change. The feedback is controlled by f = α(w + x)/(1 + s(w + x)), γ is the ratio between the population relaxation rate and the photon detuning, ε is the high-pass frequency in the feedback loop, δ0 is the solitary laser threshold, s is a saturation coefficient of the amplifier and α is a coefficient proportional to the photodetector responsivity. In our simulations we fix α = 1, γ = 1 × 10−3, ε = 2 × 10−5, δ0 = 1.017 and s = 11, values for which chaotic dynamics is observed experimentally32.
are corresponding rate of change. The feedback is controlled by f = α(w + x)/(1 + s(w + x)), γ is the ratio between the population relaxation rate and the photon detuning, ε is the high-pass frequency in the feedback loop, δ0 is the solitary laser threshold, s is a saturation coefficient of the amplifier and α is a coefficient proportional to the photodetector responsivity. In our simulations we fix α = 1, γ = 1 × 10−3, ε = 2 × 10−5, δ0 = 1.017 and s = 11, values for which chaotic dynamics is observed experimentally32.
As before, Eqs (3)–(5), were solved numerically with the fourth-order Runge-Kutta algorithm and fixed time-step h = 0.05. The first 107 time-steps were discarded as transient and the LVs were computed for 9.5 × 105 times-steps (including forward and backward time motion).
Figure 4 shows a typical trajectory with colors representing the values of θ23 for every point of the trajectory. We started from (x0, y0, w0) = (1, 1.5, 0.5) and observed a small spiraling-out motion in the (x, y) coordinates, then an abrupt increase of w, and then a larger spiraling-in motion leading to the reinjection process. It is easy to realize that when w increases, θ23 changes colors and assumes values approaching 0 or π. This can be more easily observed in the time evolution of w shown in Fig. 5 (in units of 104 time intervals). Figure 5(a) displays the scaled variable w′ = w × 100 and Fig. 5(b), for the same times, presents the θ12 (red line) and θ23 (blue line). Comparing Fig. 5(a) and (b) we observe that preceding all large peaks in w, one finds θ12 → 0 and, simultaneously, θ23 → π. Note that in contrast to the Rössler’s system, in this case both stable and unstable manifolds align along the direction of flow. Thus, once again, the LVs from the stable and unstable manifolds tend to align along the flow direction before large-amplitude events. In other words, large peaks of w occur shortly after the alignment of stable and unstable manifold along the flow direction. As seen in Fig. 5(b), in this case both the alert and catastrophe times (i.e. prediction times) can be close to each other. On average, prediction of large peaks occurs at about 1 time unit (104 time-steps).
Discussion
The alignment of LVs along the flow direction provides a straightforward and apparently reliable means of predicting catastrophic events in chaotic dynamical systems. This was corroborated for two familiar dynamical systems, namely a Rössler oscillator, and a semiconductor laser with electronic feedback. We are not aware of any other quantitative criterion able to predict large-amplitude events.
To predict large-amplitude events, one should evolve a trajectory and monitor  . Whenever its magnitude becomes larger than a suitable system-dependent threshold, a peak should be expected. To estimate the peak intensity, evolve the trajectory further and check how close θ23 approaches 0 or π. The closeness of the approach defines the peak intensity and, therefore, can anticipate a catastrophe. In realistic situations where noise is present, the validity of the alignment conditions depends on the survival of the spikes under the noise influence.
. Whenever its magnitude becomes larger than a suitable system-dependent threshold, a peak should be expected. To estimate the peak intensity, evolve the trajectory further and check how close θ23 approaches 0 or π. The closeness of the approach defines the peak intensity and, therefore, can anticipate a catastrophe. In realistic situations where noise is present, the validity of the alignment conditions depends on the survival of the spikes under the noise influence.
An open challenge is to check the effectiveness of LVs alignment to predict catastrophes for higher-dimensional systems, a considerably more complicated framework for which there are yet no efficient methods to compute angles between invariant manifolds. Nevertheless, from a theoretical point of view we anticipate no problems in predicting catastrophes regardless of the underlying dimensionality of the system. This, of course, remains to be explored.
Methods
Here, we describe briefly the essential details for the numerical implementation of the procedure to compute the angle between the two invariant subspaces of a 3D dissipative dynamical system. We are interested in the forward evolution in the tangent space of an initially orthonormal basis  . Such evolution is governed by the equation
. Such evolution is governed by the equation

where Jn = Jn−1Jn−2 … J0 is the product of the Jacobian matrix of the map evaluated for every orbital point. It is implicit here that at the initial time n = 0 we have already computed the orbit for a sufficiently long time (forward transient time) so that the orthonormal basis of the tangent space converged already to the asymptotic Gram-Schmidt (GS) vectors17. In order to avoid divergences the matrix  is renormalized for each step n. As usual, this can be done by the QR decomposition
is renormalized for each step n. As usual, this can be done by the QR decomposition

The matrix Rn is upper-triangular

and contains the information obtained in the GS orthonormalization procedure of  . Here,
. Here,  are the GS vectors after the orthonormalization. Since
are the GS vectors after the orthonormalization. Since  and
and  are orthonormal by construction, they can only provide information about the local rates of expansion (contraction) of the vectors, stored in the diagonal elements of Rn, from which the standard Lyapunov exponents can be obtained. However, to calculate the angle between the invariant subspaces in the tangent space, we need the LVs determined from the relations
are orthonormal by construction, they can only provide information about the local rates of expansion (contraction) of the vectors, stored in the diagonal elements of Rn, from which the standard Lyapunov exponents can be obtained. However, to calculate the angle between the invariant subspaces in the tangent space, we need the LVs determined from the relations



The coefficients  are determined from the dynamics in tangent space for the backward direction. In the matrix form we have
are determined from the dynamics in tangent space for the backward direction. In the matrix form we have  , where
, where  is the inverse of the Rj matrix obtained from the GS orthonormalization procedure in the forward evolution, Eq. (8). The time j starts to count after the backward transient, which is the time in the backward evolution sufficiently long to converge the tangent initial conditions close to the LVs. The LVs have normalized length so that the columns of
is the inverse of the Rj matrix obtained from the GS orthonormalization procedure in the forward evolution, Eq. (8). The time j starts to count after the backward transient, which is the time in the backward evolution sufficiently long to converge the tangent initial conditions close to the LVs. The LVs have normalized length so that the columns of  must be normalized to 1. The initial condition for Cn, before starting the backward evolution, can be a generic nonsingular upper triangular matrix, which is the GS basis.
must be normalized to 1. The initial condition for Cn, before starting the backward evolution, can be a generic nonsingular upper triangular matrix, which is the GS basis.
Additional Information
How to cite this article: Beims, M. W. and Gallas, J. A. C. Alignment of Lyapunov Vectors: A Quantitative Criterion to Predict Catastrophes? Sci. Rep. 6, 37102; doi: 10.1038/srep37102 (2016).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
R. D. Peters, M. Le Berre & Y. Pomeau . Prediction of catastrophes: An experimental model. Phys. Rev. E 86, 026207 (2012).
S. Albeverio, V. Jentsch & H. Kantz . Editors, Extreme Events in Nature and Society. (Springer, New York, 2006).
For a survey see, e.g., N. Akhmediev et al. Roadmap on optical rogue waves and extreme events. J. Opt. 18, 063001 and references therein (2016).
E. Mercier, A. Even, E. Mirisola, D. Wolfersberger & M. Sciamanna . Numerical study of extreme events in a laser diode with optical feedback. Phys. Rev. E 91, 042914 (2015).
S. Perrone, R. Vilaseca, J. Zamora-Munt & C. Masoller . Controlling the likelihood of rogue waves in an optically injected semiconductor laser via direct current modulation. Phys. Rev. A 89, 033804 (2014).
F. Selmi et al. Spatiotemporal chaos induces extreme events in microcavity laser. Phys. Rev. Lett. 116, 013901 (2016).
U. Ravitej & M. Sushil . Physical manifestation of extreme events in random lasers. Opt. Lett. 40, 5046–5049 (2015).
M. Mattheakis, I. J. Pitsios, G. P. Tsironis & S. Tzortzakis . Extreme events in complex linear and nonlinear photonic media. Chaos, Solitons & Fractals 84, 73–80 (2016).
C. Liu et al. Triggering extreme events at the nanoscale in photonic seas. Nature Phys. 11, 358–363 (2015).
M. Conforti et al. Turbulent dynamics of an incoherently pumped passive optical fiber cavity: Quasisolitons, dispersive waves, and extreme events. Phys. Rev. A 91, 023823 (2015).
S. Bialonski, G. Ansmann & H. Kantz . Data-driven prediction and prevention of extreme events in a spatially extended excitable system. Phys. Rev. E 92, 042910 (2015).
N. Marwan & J. Kurths . Complex network based techniques to identify extreme events and (sudden) transitions in spatio-temporal systems. Chaos 25, 097609 (2015).
K. W. Bannister et al. Real-time detection of an extreme scattering event: Constraints on galactic plasma lenses. Science 351, 354–356 (2016).
B. Ph. van Milligen, B. A. Carreras & D. E. Newman . Constructing criteria to diagnose the likelihood of extreme events in the case of the electric power grid. Chaos 26, 033109 (2016).
Y.-Z. Chen, Z.-G. Huang, H.-F. Zhang, D. Eisenberg, T. P. Seager & Y.-C. Lai . Extreme events in multilayer, interdependent complex networks and control. Sci. Rep. 5, 17277 (2015).
Y. Pomeau, A. Pumir & P. Pelce . Intrinsic stochasticity with many degrees of freedom. J. Stat. Phys. 37, 39–49 (1984).
C. L. Wolfe & R. M. Samelson . Method for recovering Lyapunov vectors from singular vectors. Tellus A 59, 355–366 (2007).
A. Norwood et al. Lyapunov, singular and bred vectors in a multi-scale system an empirical exploration of vectors related to instabilities. J. Phys. A 46, 254021 (2013).
F. Ginelli, H. Chaté, R. Livi & A. Politi . Covariant Lyapunov vectors. J. Phys. A 46, 254005, and references therein (2013).
M. W. Beims & J. A. C. Gallas . Manifold angles, the concept of self-similarity, and angle-enhanced bifurcation diagrams. Sci. Rep. 6, 18859 (2016).
P. V. Kuptsov & S. P. Kuznetsov . Predictable nonwandering localization of covariant Lyapunov vectors and cluster synchronization in scale-free networks of chaotic maps. Phys. Rev. E 90, 032901 (2014).
A. Trevisan & F. Pancotti . Periodic orbits, Lyapunov vectors, and singular vectors in the Lorenz system. J. Atmos. Sci. 55, 390–398 (1998).
M. Inubuschi, S. Takehiro & M. Yamada . Regeneration cycle and the covariant Lyapunov vectors in a minimal wall turbulence. Phys. Rev. E 92, 023022 (2015).
R. S. Hansen & S. Hannestad . Chaotic flavor evolution in an interacting neutrino gas. Phys. Rev. D 90, 025009 (2014).
D. P. Truant & G. P. Morris . Backward and covariant Lyapunov vectors and exponents for hard-disk systems with a steady heat current. Phys. Rev. E 90, 052907 (2014).
L. Palatella, A. Trevisan & S. Rambaldi . Nonlinear stability of traffic models and the use of Lyapunov vectors for estimating the traffic state. Phys. Rev. E 88, 022901 (2013).
C. A. Jousseph et al. Weak dissipative effects on trajectories from the edge of basins of attraction. Physica A. 456, 68–74 (2016).
J. Argyris, G. Faust, M. Haase & R. Friedrich . An Exploration of Dynamical Systems and Chaos. 2nd ed. (Springer, New York, 2015).
J. A. C. Gallas . The structure of infinite periodic and chaotic hub cascades in phase diagrams of simple autonomous flows. Int. J. Bif. Chaos 20, 197–211 (2010).
P. Glendinning . Stability, Instability and Chaos. (Cambridge University Press, Cambridge, England, 1994).
J. G. Freire & J. A. C. Gallas . Non-Shilnikov cascades of spikes and hubs in a semiconductor laser with optoelectronic feedback. Phys. Rev. E 82, 037202 (2010).
K. Al-Naimee, F. Marino, M. Ciszak, R. Meucci & F. T. Arecchi . Chaotic spiking and incomplete homoclinic scenarios in semiconductor lasers with optoelectronic feedback. New J. Phys. 11, 073022 (2009).
Acknowledgements
This work was supported by the Max-Planck Institute for the Physics of Complex Systems, Dresden, in the framework of the Advanced Study Group on Optical Rare Events, and by the Deutsche Forschungsgemeinschaft (DFG) through the Cluster of Excellence Engineering of Advanced Materials. The authors were supported by CNPq, Brazil.
Author information
Authors and Affiliations
Contributions
M.W.B. and J.A.C.G. conceived the simulations. M.W.B. performed the simulations. Both authors discussed the results and wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Beims, M., Gallas, J. Alignment of Lyapunov Vectors: A Quantitative Criterion to Predict Catastrophes?. Sci Rep 6, 37102 (2016). https://doi.org/10.1038/srep37102
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep37102
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.




 . P refers to predicted as large spike while NP refers to a peak detected but non-predicted as large, according to the choice of thresholds (see text). The horizontal line marks π.
. P refers to predicted as large spike while NP refers to a peak detected but non-predicted as large, according to the choice of thresholds (see text). The horizontal line marks π.
 and
and  discussed in the text. Although the sequence of zmax is randomly distributed in time, both branches are symmetric.
discussed in the text. Although the sequence of zmax is randomly distributed in time, both branches are symmetric.
