Abstract
The uncertainty principle is one of the characteristic properties of quantum theory based on incompatibility. Apart from the incompatible relation of quantum states, mutually exclusiveness is another remarkable phenomenon in the information- theoretic foundation of quantum theory. We investigate the role of mutual exclusive physical states in the recent work of stronger uncertainty relations for all incompatible observables by Mccone and Pati and generalize the weighted uncertainty relation to the product form as well as their multi-observable analogues. The new bounds capture both incompatibility and mutually exclusiveness, and are tighter compared with the existing bounds.
Similar content being viewed by others
Introduction
Heisenberg’s uncertainty principle1 is one of the fundamental notions in quantum theory. The original form is a result of noncommutativity of the position and momentum operators. Robertson’s formulation of Heisenberg’s uncertainty principle in matrix mechanics2 states that for any pair of observables A and B with bounded spectrums, the product of standard deviations of A and B is no less than half of the modulus of the expectation value of their commutator:

where  is the standard deviation of the self-adjoint operator A. Here the expectation value
is the standard deviation of the self-adjoint operator A. Here the expectation value  is over the state
is over the state  for any observable
for any observable  . In fact, Robertson’s uncertainty relation can be derived from a slightly strengthened Schrödinger uncertainty inequality3
. In fact, Robertson’s uncertainty relation can be derived from a slightly strengthened Schrödinger uncertainty inequality3

where  .
.
Besides their importance in quantum mechanics, uncertainty relations play a significant role in quantum information theory as well4,5,6,7,8,9,10. The variance-based uncertainty relations possess clear physical meanings and have a variety of applications in quantum information processings such as quantum spin squeezing11,12,13,14,15, quantum metrology16,17,18, and quantum nonlocality19,20.
While the early forms of variance-based uncertainty relations are vital to the foundation of quantum theory, there are two problems still need to be addressed: (1) Homogeneous product of variances may not fully capture the concept of incompatibility. In other words, a weighted relation may produce a better approximation (e.g., the uncertainty relation with Rényi entropy21 and variance-based uncertainty relation for a weighted sum), for more details and examples, see ref. 22; (2) The existing variance-based uncertainty relations are far from being tight, and improvement is needed. One also needs to know how to generalize the product form to the case of multiple observables for practical applications.
In ref. 22, the authors and collaborators have proposed weighted uncertainty relations to answer the first question and succeeded in improving the uncertainty relation. Let’s recall the weighted uncertainty relation for the sum of variances. For arbitrary two incompatible observables A, B and any real number λ, the following inequality holds

with

and

where  ,
,  ,
,  and
and  are orthogonal to |ψ〉. In information-theoretic context, it is also natural to quantify the uncertainty by weighted products of variances, which also help to estimate individual variance as in ref. 22.
are orthogonal to |ψ〉. In information-theoretic context, it is also natural to quantify the uncertainty by weighted products of variances, which also help to estimate individual variance as in ref. 22.
Recently, Maccone and Pati obtained an amended Heisenberg-Robertson inequality23:

which is reduced to Heisenberg-Robertson’s uncertainty relation when minimizing the lower bound over  , and the equality holds at the maximum. This amended inequality gives rise to a stronger uncertainty relation for almost all incompatible observables, and the improvement is due to the special vector
, and the equality holds at the maximum. This amended inequality gives rise to a stronger uncertainty relation for almost all incompatible observables, and the improvement is due to the special vector  perpendicular to the quantum state |ψ〉. We notice that this can be further improved by using the mutually exclusive relation between
perpendicular to the quantum state |ψ〉. We notice that this can be further improved by using the mutually exclusive relation between  and |ψ〉. Moreover, this idea can be generalized to the case of multi-observables. For this reason the strengthen uncertainty relation thus obtained will be called a mutually exclusive uncertainty relation.
and |ψ〉. Moreover, this idea can be generalized to the case of multi-observables. For this reason the strengthen uncertainty relation thus obtained will be called a mutually exclusive uncertainty relation.
The goal of this paper is to answer the aforementioned questions to derive the product form of the weighted uncertainty relation, and investigate the physical meaning and applications of the mutual exclusive physical states in variance-based uncertainty relations. Moreover, we will generalize the product form to multi-observables to give tighter lower bounds.
Results
We first generalize the weighted uncertainty relations from the sum form22 to the product form, and then introduce mutually exclusive uncertainty relations (MEUR). After that we derive a couple of lower bounds based on Mutually exclusive physical states (MEPS), and we show that our results outperform the bound in ref. 23, which has been experimentally tested recently24. Finally, generalization to multi-observables is also given.
We start with the sum form of the uncertainty relation, which takes equal contribution of the variance from each observable. However, almost all variance-based uncertainty relations do not work for the general situation of incompatible observables, and they often exclude important cases. In ref. 22, the authors and collaborators solved this degeneracy problem by considering weighted uncertainty relations to measure the uncertainty in all cases of incompatible observables. Using the same idea, we will study the product form of weighted uncertainty relations to give new and alternative uncertainty relations in the general situation. The corresponding mathematical tool is the famous Young’s inequality. The new weighted uncertainty is expected to reveal the lopsided influence from observables. They contain the usual homogeneous relation of ΔA2ΔB2 as a special case.
Theorem 1. Let A, B be two observables such that ΔAΔB > 0, and p, q two real numbers such that  . Then the following weighted uncertainty relation for the product of variances holds.
. Then the following weighted uncertainty relation for the product of variances holds.

where p < 1, and the equality holds if and only if ΔA = ΔB. If p > 1, then  becomes a upper bound for the weighted product.
becomes a upper bound for the weighted product.
See Methods for a proof of Theorem 1.
The weighted uncertainty relations for the product of variances have a desirable feature: our measurement of incompatibility is weighted, which fits well with the reality that observables usually don’t always reach equilibrium, i.e., in physical experiments their contributions may not be the same (cf. ref. 22). As an illustration, let us consider the relative error function between the uncertainty and weighted bound, which is defined by

In general f is a function of both p and |ψ〉. It is hard to find its extremal points as it involves in partial differential equations. Also the extremal points hardly occur at homogeneous weights, so incompatible observables usually don’t contribute equally to the uncertainty relation, which explains the need for a weighted uncertainty relation in the product form.
In what follows, we show how to tighten Maccone and Pati’s amended Heisenberg-Robertson uncertainty relation23 by regarding mutually exclusive physical states as another information resource, and then generalize the variance-based uncertainty relation to the case of multi-observables.
We will refer to (6) as a mutually exclusive uncertainty relation since the states |ψ〉 and  represent two mutual exclusive states in quantum mechanics, which is the main reason for improving the tightness of the bound. Next we move further to improve the bound by combining mutually exclusive relations and weighted relations.
represent two mutual exclusive states in quantum mechanics, which is the main reason for improving the tightness of the bound. Next we move further to improve the bound by combining mutually exclusive relations and weighted relations.
Maccone and Pati’s uncertainty relation can be viewed as a singular case in a family of uncertainty relations parameterized by positive variable λ, which corresponds to our recent work on weighted sum of uncertainty relations22. We proceed similarly as the case of the amended Heisenberg-Robertson uncertainty relation by considering a modified square-modulus and Holevo inequalities in Hilbert space25 in the following result.
Theorem 2. Let A and B be two incompatible observables and |ψ〉 a fixed quantum state. Then the mutually exclusive uncertainty relation holds:

for any unit vector  perpendicular to |ψ〉 and arbitrary parameter λ > 0.
perpendicular to |ψ〉 and arbitrary parameter λ > 0.
See Methods for a proof of Theorem 2.
The obtained variance-based uncertainty relation is stronger than Maccone and Pati’s amended uncertainty relation. In fact, when the maximal value  is reached at a point λ0 ≠ 1, the new bound is stronger than that of Maccone-Pati’s amended uncertainty relation. Let
is reached at a point λ0 ≠ 1, the new bound is stronger than that of Maccone-Pati’s amended uncertainty relation. Let  (i = 1, 2) be two lower bounds given in the RHS of (8), define the tropical sum
(i = 1, 2) be two lower bounds given in the RHS of (8), define the tropical sum

This gives a tighter lower bound when the maximal value of  is reached at different direction in Hψ (hyperplane orthogonal to |ψ〉) for
is reached at different direction in Hψ (hyperplane orthogonal to |ψ〉) for  . In other words, the new lower bound is a piecewise defined function of MEPS
. In other words, the new lower bound is a piecewise defined function of MEPS  taking the maximum of the two bounds. In particular, for λ0 ≠ 1, the tropical sum
taking the maximum of the two bounds. In particular, for λ0 ≠ 1, the tropical sum  offers a better lower bound than
offers a better lower bound than  , the Maccone-Pati’s lower bound. Note that
, the Maccone-Pati’s lower bound. Note that  may have a smaller minimum value than
may have a smaller minimum value than  when λ ≠ 1, as
when λ ≠ 1, as  , while the minimum value of
, while the minimum value of  is just the bound for Heisenberg-Robertson’s uncertainty relation. Because we only consider the maximum, it does not affect our result.
is just the bound for Heisenberg-Robertson’s uncertainty relation. Because we only consider the maximum, it does not affect our result.
For example, consider a 4-dimensional system with state  ,
,  and take the following observables
and take the following observables

Direct calculation gives

and

For  and
and  , set
, set

and

both of them have modulus one, then

meanwhile

so

Both the lower bounds  and
and  are functions of MEPS
are functions of MEPS  . However, for each
. However, for each  ,
,  gives a better approximation of ΔAΔB than
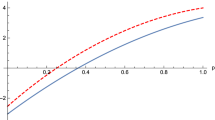
gives a better approximation of ΔAΔB than  . Figure 1 is a schematic diagram of these two lower bounds. It is clear that
. Figure 1 is a schematic diagram of these two lower bounds. It is clear that  provides a closer estimate to ΔAΔB:
provides a closer estimate to ΔAΔB:

for any unit MEPS  orthogonal to |ψ〉. This is due to the fact that the bound
orthogonal to |ψ〉. This is due to the fact that the bound  is continuous on both MEPS
is continuous on both MEPS  and λ, which shows the advantage of our mutually exclusive uncertainty principle. The shadow region in Fig. 2. illustrates the outline of ΔAΔB and our bound
and λ, which shows the advantage of our mutually exclusive uncertainty principle. The shadow region in Fig. 2. illustrates the outline of ΔAΔB and our bound  .
.
In Fig. 3, we illustrate our results, showing how the obtained bound  outperforms the recent work of ref. 26 as well as the Schrödinger uncertainty relation. We consider the angular momenta Lx and Ly for spin-1 particle with state |ψ〉 = cos θ |1〉 − sin θ |0〉 and
outperforms the recent work of ref. 26 as well as the Schrödinger uncertainty relation. We consider the angular momenta Lx and Ly for spin-1 particle with state |ψ〉 = cos θ |1〉 − sin θ |0〉 and  = sin θ |1〉 + cos θ |0〉, where |0〉 and |1〉 are eigenstates of the angular momentum Lz.
= sin θ |1〉 + cos θ |0〉, where |0〉 and |1〉 are eigenstates of the angular momentum Lz.
Mutually exclusive physical states with different directions in Hψ offer different kinds of mutually exclusive information and improvement of the uncertainty relation. When such an experiment of the mutually exclusive uncertainty relation is performed, one is expected to have infinitely many strong lower bounds of the variance-based uncertainty relation.
Now we further generalize the uncertainty relations to multi-observables. For simplicity, write

So

is continuous on both MEPS  and λ. Repeatedly using (8) for
and λ. Repeatedly using (8) for  and λjk, we obtain the following relation.
and λjk, we obtain the following relation.
Theorem 3. Let A1, A2, …, An be n incompatible observables, |ψ〉 a fixed quantum state and λjk positive real numbers, we have

for any MEPS  orthogonal to |ψ〉 with modulus one. If some
orthogonal to |ψ〉 with modulus one. If some  is negative, a negative sign is inserted into the RHS of (14) to ensure positivity. The equality holds if and only if MEPS
is negative, a negative sign is inserted into the RHS of (14) to ensure positivity. The equality holds if and only if MEPS  for all j > k.
for all j > k.
As a corollary, Theorem 3 leads to a simple bound of the uncertainty relation for multi-observables.
Corollary 1. Let A1, A2, …, An be n incompatible observables, then the following uncertainty relation holds

See Methods for a proof of Corollary 1.
Next, we provide yet another mutually exclusive uncertainty relation.
Theorem 4. Let A and B be two incompatible observables and |ψ〉 a fixed quantum state. Then

for any unit MEPS  orthogonal to |ψ〉, with
orthogonal to |ψ〉, with

where MEPS  are unit vectors in Hψ.
are unit vectors in Hψ.
See Methods for a proof of Theorem 4.
Obviously, (16) can be seen as an amended Schrödinger inequality and also offers a better bound than (2) and Maccone-Pati’s relation (6). Figure 4 illustrates the schematic comparison.
In general, if there exists an operator M for A and B such that 〈M〉 = 0,  , then we have the following:
, then we have the following:
Remark 1. Let A and B be two incompatible observables and |ψ〉 a fixed quantum state. We claim the following mutually exclusive uncertainty relation holds:

Eq. (18) also gives a generalized Schrödinger uncertainty relation. Here as usual MEPS  is any unit vector perpendicular to |ψ〉. The proof of Theorem 4 and Remark 1 are similar to that of Theorem 2, so we sketch it here. It is easy to see that the RHS of (18) reduces to the lower bound of Schrödinger’s uncertainty relation (2) when minimizing over
is any unit vector perpendicular to |ψ〉. The proof of Theorem 4 and Remark 1 are similar to that of Theorem 2, so we sketch it here. It is easy to see that the RHS of (18) reduces to the lower bound of Schrödinger’s uncertainty relation (2) when minimizing over  , and the equality holds at the maximum. The corresponding uncertainty relation for arbitrary n observables is the following result.
, and the equality holds at the maximum. The corresponding uncertainty relation for arbitrary n observables is the following result.
Theorem 5. Let A1, A2, …, An be n incompatible observables, |ψ〉 a fixed quantum state and λjk positive real numbers. Then we have that

where Mjk satisfy 〈Mjk〉 = 0,  and MEPS
and MEPS  orthogonal to |ψ〉 with modulus one.
orthogonal to |ψ〉 with modulus one.
The RHS of (19) has the minimum value

and the equality holds at the maximum. Therefore one obtains the following corollary.
Corollary 2. Let A1, A2, …, An be n incompatible observables, then the following uncertainty relation holds

See Methods for a proof of Corollary 2.
We note that our enhanced Schrödinger uncertainty relations offer significantly tighter lower bounds than that of Maccone-Pati’s uncertainty relations for multi-observables, as our lower bound contains an extra term of  (compare (1) with (2)).
(compare (1) with (2)).
Finally, we remark that we can also replace the non-hermitian operator  in (6) by a hermitian one. A natural consideration is the amended uncertainty relation
in (6) by a hermitian one. A natural consideration is the amended uncertainty relation

for any unit MEPS  perpendicular to |ψ〉. The corresponding uncertainty relation for multi-observables can also be generalized.
perpendicular to |ψ〉. The corresponding uncertainty relation for multi-observables can also be generalized.
The minimum of Maccone and Pati’s amended bound  in the RHS of (6) agrees with the bound in Heisenberg-Robertson’s uncertainty relation, which is weaker than Schrödinger’s bound in (2). We point out that the bound given as a continuous function of MEPS’s will always produce a better lower bound. In fact, the continuity of
in the RHS of (6) agrees with the bound in Heisenberg-Robertson’s uncertainty relation, which is weaker than Schrödinger’s bound in (2). We point out that the bound given as a continuous function of MEPS’s will always produce a better lower bound. In fact, the continuity of  in MEPS
in MEPS  implies that there exists suitable
implies that there exists suitable  such that
such that  is tighter than the bound of Heisenberg-Robertson’s uncertainty relation. Similarly our lower bound given in (27) or more generally in (18) provides a tighter lower bound than the enhanced Schrödinger’s uncertainty relation (2). This shows the advantage of lower bounds with MEPS’s. Furthermore, lower bounds with more variables give better estimates for the product of variances of observables, as in (19).
is tighter than the bound of Heisenberg-Robertson’s uncertainty relation. Similarly our lower bound given in (27) or more generally in (18) provides a tighter lower bound than the enhanced Schrödinger’s uncertainty relation (2). This shows the advantage of lower bounds with MEPS’s. Furthermore, lower bounds with more variables give better estimates for the product of variances of observables, as in (19).
Conclusions
The Heisenberg-Robertson uncertainty relation is a fundamental principle of quantum theory. It has been recently generalized by Maccone and Pati to an enhanced uncertainty relation for two observables via mutually exclusive physical states. Based on these and weighted uncertainty relations22, we have derived uncertainty relations for the product of variances from mutually exclusive physical states (MEPS) and offered tighter bounds.
In summary, we have proposed generalization of variance-based uncertainty relations. By virtue of MEPS, we have introduced a family of infinitely many Schrödinger-like uncertainty relations with tighter lower bounds for the product of variances. Indeed, our mutually exclusive uncertainty relations can be degenerated to the classical variance-based uncertainty relations by fixing MEPS and the weight. Also, our study further shows that the mutually exclusiveness between states is a promising information resource.
Methods
Proof of Theorem 1. To prove the theorem, we recall Young’s inequality27: for  , p < 1 one has that
, p < 1 one has that

Note that the right-hand side (RHS) may be negative if p < 1. But this can be avoided by using the symmetry of Young’s inequality to get

Thus our bound is nontrivial. We remark that if p > 1, it is directly from the Young’s inequality27

and equality holds in (22) and (23) only when ΔA = ΔB. ■
Proof of Theorem 2. Here we provide two proofs of the proposed mutually exclusive uncertainty relation (8). The first one, based on weighted relations22, is a natural deformation of ref. 23 and is sketched as follows. By maximizing the RHS of (8), we see that the maximum ΔAΔB is achieved when the mutually exclusive physical state (MEPS)  . Clearly our uncertainty relation contains (6) as a special case of λ = 1.
. Clearly our uncertainty relation contains (6) as a special case of λ = 1.
The second proof uses geometric property and is preferred because of its mathematical simplicity and also working for the amended Heisenberg-Robertson uncertainty relation23. In fact, the RHS of (6), denoted by  , is a continuous function of λ and the unit MEPS
, is a continuous function of λ and the unit MEPS  . By the vector projection, the maximum value ΔAΔB of
. By the vector projection, the maximum value ΔAΔB of  over the hyperplane of
over the hyperplane of  is attained when
is attained when  . Therefore for any λ > 0
. Therefore for any λ > 0

where  is the RHS of (6). Similarly
is the RHS of (6). Similarly

for any λ > 0 and the equality holds if λ = 1, which implies (8) and completes the second proof. ■
Proof of Corollary 1. Obviously, taking the minimum of (14) over MEPS  implies that
implies that

When λjk = 1 for all j > k, the minimum is  . Meanwhile if λjk and MEPS
. Meanwhile if λjk and MEPS  vary, Eq. (14) provides a family of mutually exclusive uncertainty relations for arbitrary n observables with (24) as the lower bound. ■
vary, Eq. (14) provides a family of mutually exclusive uncertainty relations for arbitrary n observables with (24) as the lower bound. ■
Proof of Theorem 4. By the same method used in deriving (8) it follows that  , and
, and  is
is

which equals to the lower bound of the Schrödinger uncertainty (2). We can modify g into a function with the same maximum and lower bound as Schrödinger’s uncertainty relation. Note that s ≤ ΔA2ΔB2, then

which is equivalent to (by solving ΔA2ΔB2)

for any unit MEPS  orthogonal to |ψ〉. In fact, let
orthogonal to |ψ〉. In fact, let  be the RHS of (27). It is easy to see that
be the RHS of (27). It is easy to see that  and
and

Hence we have the mutually exclusive uncertainty relation appeared in (27). ■
Proof of Corollary 2. Apparently, taking the minimum of (19) over MEPS  implies that
implies that

with the minimum is  . Meanwhile if the MEPS
. Meanwhile if the MEPS  vary, Eq. (19) provides a family of mutually exclusive uncertainty relations for arbitrary n observables with (28) as the lower bound. ■
vary, Eq. (19) provides a family of mutually exclusive uncertainty relations for arbitrary n observables with (28) as the lower bound. ■
Additional Information
How to cite this article: Xiao, Y. and Jing, N. Mutually Exclusive Uncertainty Relations. Sci. Rep. 6, 36616; doi: 10.1038/srep36616 (2016).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 43, 172 (1927).
Robertson, H. P. The Uncertainty Principle. Phys. Rev. 34, 163 (1929).
Schrödinger, E. Zum Heisenbergschen Unschärfeprinzip. Ber. Kgl. Akad. Wiss. Berlin 24, 296 (1930).
Busch, P., Heinonen, T. & Lahti, P. J. Heisenberg’s uncertainty principle. Phys. Rep. 452, 155 (2007).
Busch, P., Lahti, P. & Werner, R. Colloquium: Quantum root-mean-square error and measurement uncertainty relations. Rev. Mod. Phys. 86, 1261 (2014).
Białynicki-Birula, I. & Mycielski, J. Uncertainty relations for information entropy in wave mechanics. Comm. Math. Phys. 44, 129 (1975).
Deutsch, D. Uncertainty in quantum measurements. Phys. Rev. Lett. 50, 631 (1983).
Wehner, S. & Winter, A. Entropic uncertainty relations-a survey. New J. Phys. 12, 025009 (2010).
Ghirardi, G. C., Marinatto, L. & Romano, R. An optimal entropic uncertainty relation in a two-dimensional Hilbert space. Phys. Lett. A 317, 32 (2003).
Bosyk, G. M., Portesi, M. & Plastino, A. Collision entropy and optimal uncertainty. Phys. Rev. A 85, 012108 (2012).
Walls, D. F. & Zoller, P. Reduced quantum fluctuations in resonance. Phys. Rev. Lett. 47, 709 (1981).
Wódkiewicz, K. & Eberly, J. Coherent states, squeezed fluctuations, and the SU(2) am SU(1,1) groups in quantum-optics applications. J. Opt. Soc. Am. B 2, 458 (1985).
Wineland, D. J., Bollinger, J. J., Itano, W. M., Moore, F. L. & Heinzen, D. J. Spin squeezing and reduced quantum noisd in spectroscopy. Phys. Rev. A 46 R6797 (1992).
Kitagawa, M. & Ueda, M. Squeezed spin states. Phys. Rev. A 47, 5138 (1993).
Ma, J., Wang, X. G., Sun, C. P. & Nori, F. Quantum spin squeezing. Phys. Rep. 509, 89 (2011).
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum-enhanced measurements: beating the standard quantum limit. Science 306, 1330 (2004).
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum metrology. Phys. Rev. Lett. 96, 010401 (2006).
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photon. 5, 222 (2011).
Oppenheim, J. & Wehner, S. The uncertainty principle determines the nonlocality of quantum mechanics. Science. 330, 1072 (2010).
Li, J.-L., Du, K. & Qiao, C.-F. Ascertaining the uncertainty relations via quantum correlations. J. Phys. A 47, 085302 (2014).
Maassen, H. & Uffink, J. B. M. Generalized entropic uncertainty relations. Phys. Rev. Lett. 60, 1103 (1988).
Xiao, Y., Jing, N., Li-Jost, X. & Fei, S.-M. Weighted uncertainty relations. Sci. Rep. 6, 23201 (2016).
Maccone, L. & Pati, A. K. Stronger uncertainty relation for all incompatible observables. Phys. Rev. Lett. 113, 260401 (2014).
Wang, K., Zhan, X., Bian, Z., Li, J., Zhang, Y. & Xue, P. Experimental investigation of the stronger uncertainty relations for all incompatible observables. Phys. Rev. A. 93, 052108 (2016).
Holevo, A. S. A generalization of the Rao-Cramér inequality. Teor. Veroyatnost. i Primenen. 18, 371 (1973) Probab. Appl. 18, 359 (1974).
Mondal, D., Bagchi, S. & Pati, A. K. Tighter uncertainty and reverse uncertainty relations. arXiv: 1607.06712v1.
Zorich, V. A. Mathematical Analysis 1. (Springer, Berlin, 2015).
Acknowledgements
We thank Jian Wang, Yinshan Chang, Xianqing Li-Jost and Shao-Ming Fei for fruitful discussions. The work is supported by National Natural Science Foundation of China (Grants Nos 11271138 and 11531004), China Scholarship Council and Simons Foundation Grant No. 198129.
Author information
Authors and Affiliations
Contributions
Y.X. and N.J. analyzed and wrote the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Xiao, Y., Jing, N. Mutually Exclusive Uncertainty Relations. Sci Rep 6, 36616 (2016). https://doi.org/10.1038/srep36616
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep36616
This article is cited by
-
Strong majorization uncertainty relations and experimental verifications
npj Quantum Information (2023)
-
Tighter sum uncertainty relations via variance and Wigner–Yanase skew information for N incompatible observables
Quantum Information Processing (2021)
-
Tight N-observable uncertainty relations and their experimental demonstrations
Scientific Reports (2019)
-
On noise-resolution uncertainty in quantum field theory
Scientific Reports (2017)
-
A Stronger Multi-observable Uncertainty Relation
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.



 resp.
resp. is the upper boundary above the shadow, and the red and green ones are
is the upper boundary above the shadow, and the red and green ones are  and Maccone-Pati’s bound
and Maccone-Pati’s bound  resp.
resp.
 , the shadow region is the difference between ΔAΔB and our bound
, the shadow region is the difference between ΔAΔB and our bound  . Other bounds are shown in different colors.
. Other bounds are shown in different colors.
 , the bound given by
, the bound given by 