Abstract
The topological structure of the wavefunctions of particles in periodic potentials is characterized by the Berry curvature Ωkn whose integral on the Brillouin zone is a topological invariant known as the Chern number. The bulk-boundary correspondence states that these numbers define the number of edge or surface topologically protected states. It is then of primary interest to find experimental techniques able to measure the Berry curvature. However, up to now, there are no spectroscopic experiments that proved to be capable to obtain information on Ωkn to distinguish different topological structures of the bulk wavefunctions of semiconducting materials. Based on experimental results of the dipolar matrix elements for graphene, here we show that ARPES experiments with the appropriate x-ray energies and polarization can unambiguously detect changes of the Chern numbers in dynamically driven graphene and graphene-like materials opening new routes towards the experimental study of topological properties of condensed matter systems.
Similar content being viewed by others
Introduction
Topology plays a central role in defining the structure of the ground state of condensed matter systems, the nature of the excitations and their response to external probes1,2,3,4. For particles in periodic potentials, like electrons in solids, cold atoms systems or photonic crystals, the topology of the Bloch wavefunctions is related to the geometric or Berry phase acquired by the particle as it moves along a closed path in reciprocal space5. Within a given energy band, these phases are characterized by the Berry curvature (Ωkn) whose integral over the Brillouin zone (BZ) is a topological invariant, the Chern number.
According to the bulk-boundary correspondence principle, the Chern numbers determine the unbalance in the number of chiral edge (or surface) states1. Experimentally, it has been easier to study the effects of a non-trivial topology, i.e. the emergence of such chiral edge states, rather than its origin: the structure of the Bloch wavefunctions across the whole BZ. In fact, transport and spectroscopic experiments provide direct evidence on the existence of the edge states6,7,8,9. Extracting information on Ωkn and its integral in the BZ as a measure of topology in condensed matter systems has been more elusive.
Since it is Ωkn what encodes all the information on topology and non-local effects it is natural to look for ways of obtaining direct information about this quantity—even in systems with trivial topology Ωkn is associated with anomalous velocities5,10,11 and may lead to non-local conductances and unconventional (valley) Hall effects. Ultra-cold atoms in optical lattices offer a unique playground for the study of topological band structures12 and during the last years a number of experiments focused on the study of different structures, including hexagonal lattices with bosonic and fermionic atoms. In particular, recent experiments were able to obtain a complete tomographic image of the Berry curvature of a Bloch band13. No such experiments, that require a fast switching off of the confining (lattice) potentials, are possible in solids.
The question then arises as to what experiments could give direct information on the topological structure of the Bloch wavefunctions in condensed matter systems. The high resolution angle resolved photoemission spectroscopy (ARPES) has proven to be a powerful tool to measure the dispersion relation of low energy bands7, the band structure of dynamically driven systems (Floquet spectrum)14,15, quasiparticle lifetimes and even the chiral nature of the electronic states in graphene systems16. In the latter case, ARPES experiments show that the intensity patterns have an angular dependence that give direct information of the Berry’s phase. This is due to the fact that graphene’s wavefunctions are spinors corresponding to the pseudo-spin associated with the two sublattices of the hexagonal structure. Then, close to the Dirac points, the pseudo-spin is parallel to the crystal momentum leading to a nontrivial Berry phase of π. Similar results are obtained in bilayer graphene where the winding angle is 2π. However, neither the band structure nor the Berry phase around the Dirac cones provide enough information to fully characterize the topological structure of the bands.
In what follows we show that using a pump and probe setup in graphene and graphene-like systems, photo-electrons can unveil topological phase transitions, i.e. they can unambiguously detect changes in the Chern numbers. On the one hand this is possible due to the structure of the dipole matrix elements linked to the excitation of the electrons at the π-bands of graphene. On the other hand, although Chern numbers involve the Berry curvature of all k-points in the BZ, the largest contribution comes from two hot spots—the Dirac points. As we show below, detailed analysis of the intensity of photo-electrons coming from the corners of the BZ gives the required information to identify topological transitions.
Non-trivial topologies may be generated by external magnetic fields, spin-orbit coupling or by dynamically driving a system with external time dependent fields17,18,19,20,21,22. The latter creates a new class of topological insulators known as Floquet Topological Insulators (FTI). In what follows we consider such a case.
Pump and probe experiments consist in coupling the system to an electromagnetic pump pulse followed by a short photo-exciting ARPES pulse. We consider spatially homogeneous pump pulses of circularly polarized light of frequency Ω. Typical duration of the pump pulse is δtpump ~ 250 fs. The photo-excitation due to the probe pulse occurs during the pumping time, being its duration 1/Ω < δtprobe ~ δtpump and its polarization either linear or circular.
It is instructive to start our analysis with a simple model of a gaped graphene-like system with a mass term. The pump pulse is described by a vector potential A(t) so that, for the crystal momentum k close to the K or K′ points of the BZ, the Hamiltonian reads

where  , τ = ± corresponds to the K or K′ Dirac points, respectively, and the components of σ are the Pauli matrices—in our notation the up (down) pseudo-spin corresponds to the A (B) sublattice. This model describes the band structure of graphene (with Δ = 0) and of silicene or germanene where the mass gap Δ can be induced by an external electric field23 as well as a variety of 2D materials and artificial structures24.
, τ = ± corresponds to the K or K′ Dirac points, respectively, and the components of σ are the Pauli matrices—in our notation the up (down) pseudo-spin corresponds to the A (B) sublattice. This model describes the band structure of graphene (with Δ = 0) and of silicene or germanene where the mass gap Δ can be induced by an external electric field23 as well as a variety of 2D materials and artificial structures24.
Before including the full time dependence of the pump pulse, we consider a circularly polarized monochromatic radiation described by A(t) = Re(A0 eiΩt) with  . The time dependent Schrödinger equation can be solved in the frame of the Floquet theory25,26,27,28. For states with wavevector close to the Dirac points, and to the lowest order in the field amplitude A0, the system can be described by the following Floquet Hamiltonian
. The time dependent Schrödinger equation can be solved in the frame of the Floquet theory25,26,27,28. For states with wavevector close to the Dirac points, and to the lowest order in the field amplitude A0, the system can be described by the following Floquet Hamiltonian

with

and Floquet quasi-energies  . This solution shows that at the K point (τ = +) the gap decreases as the field amplitude increases, it closes at a critical value
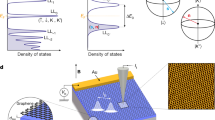
. This solution shows that at the K point (τ = +) the gap decreases as the field amplitude increases, it closes at a critical value  and increases again for A0 > Ac. On the other hand, the gap at K′ increases monotonously29. Reversing the sense of rotation of the electromagnetic field changes the Dirac point at which the gap closes. This phenomena, known as band inversion, is accompanied by a change of the nature of the Floquet wavefunctions at the corners of the BZ. While for A0 < Ac the wavefunctions of the conduction band for both cones at k = 0 are localized on the A sublattice (i.e. their pseudo-spin is up), for A0 > Ac the wavefunction at K lies on sublattice B (down pseudo-spin) as shown in Fig. 1.
and increases again for A0 > Ac. On the other hand, the gap at K′ increases monotonously29. Reversing the sense of rotation of the electromagnetic field changes the Dirac point at which the gap closes. This phenomena, known as band inversion, is accompanied by a change of the nature of the Floquet wavefunctions at the corners of the BZ. While for A0 < Ac the wavefunctions of the conduction band for both cones at k = 0 are localized on the A sublattice (i.e. their pseudo-spin is up), for A0 > Ac the wavefunction at K lies on sublattice B (down pseudo-spin) as shown in Fig. 1.
The hexagonal lattice with two sites (A and B) of the unit cell (a) and the corresponding Brillouin zone (b). In (c) the Floquet band structure near a Dirac point with the amplitude of the vector potential A0 = 0, Ac and A0 > Ac are shown; the color of the conduction and valence bands indicate the orientation of the pseudo-spin at the Dirac points. (d) The photoemission intensities at constant energy without the pump pulse (left) and with a high energy (β = 0, see text) linearly polarized probe pulse (right) show a dichroism characteristic of the chiral states; the only effect of the radiation in this configuration is to reveal the change of the constant energy surface at the K and K′ points and the appearance of Floquet replicas.
The band inversion with the closing of the gap at the critical field amplitude signals a topological phase transition29,30. Indeed the Berry curvature of the Floquet states around K and K′ is given by

and gives a contribution to the Chern number of the (Floquet) valence band  5. Hence, to this order in the field amplitude,
5. Hence, to this order in the field amplitude,  changes from 0 for A0 < Ac to 1 for A0 > Ac. When considering the full tight-binding Hamiltonian of graphene, it can be shown that in undoped nanoribbons the phase having
changes from 0 for A0 < Ac to 1 for A0 > Ac. When considering the full tight-binding Hamiltonian of graphene, it can be shown that in undoped nanoribbons the phase having  behaves as a (normal) insulator. In this phase the gap is preserved with non protected edge states laying close to the bottom and top of the energy gap. Conversely, in the phase where
behaves as a (normal) insulator. In this phase the gap is preserved with non protected edge states laying close to the bottom and top of the energy gap. Conversely, in the phase where  the gap is bridged by topologicaly protected chiral edge states and the system becomes a TI31.
the gap is bridged by topologicaly protected chiral edge states and the system becomes a TI31.
We are now in position to address the problem of how the intensity and angular dependence of the ARPES distinguishes the two different topological phases. The photo-excitation process is described by the Hamiltonian

where w(t) describes the time profile of the probe pulse,  creates a photo-electron with total momentum p and cα annihilates an electron at the sample with quantum numbers α. Assuming that the probe pulse w(t) acts in the time interval [t0, t1], the total photo-electron distribution obtained after the probe is given by16,32,33
creates a photo-electron with total momentum p and cα annihilates an electron at the sample with quantum numbers α. Assuming that the probe pulse w(t) acts in the time interval [t0, t1], the total photo-electron distribution obtained after the probe is given by16,32,33

here εp is the energy of the photo-electron,  is a state of the system in equilibrium with energy Em,
is a state of the system in equilibrium with energy Em,  is the time evolution operator including the effect of the pump pulse and f (E) is the Fermi-Dirac distribution. Only the evolution of the bulk states due to the pump perturbation is taken into account, neglecting effects of coupling of the radiation field with the final high-energy states. This effect has already been addressed in recent work15, giving rise to Volkov states. It has been pointed out that the dressing of the free-electron states can be neglected if the polarization of the pumping field is on the plane of the surface of the irradiated material. Since in our case we only consider normal incidence for the pumping field, it is correct to ignore it. The structure of the dipolar matrix elements Mpα has been discussed in ref. 16 for a probe pulse described by a vector potential with a polarization vector given by
is the time evolution operator including the effect of the pump pulse and f (E) is the Fermi-Dirac distribution. Only the evolution of the bulk states due to the pump perturbation is taken into account, neglecting effects of coupling of the radiation field with the final high-energy states. This effect has already been addressed in recent work15, giving rise to Volkov states. It has been pointed out that the dressing of the free-electron states can be neglected if the polarization of the pumping field is on the plane of the surface of the irradiated material. Since in our case we only consider normal incidence for the pumping field, it is correct to ignore it. The structure of the dipolar matrix elements Mpα has been discussed in ref. 16 for a probe pulse described by a vector potential with a polarization vector given by  . Using as a complete basis the eigenstates of the unperturbed system (α = k, τ, ± where ± indicate the valence and conduction bands, respectively) and setting
. Using as a complete basis the eigenstates of the unperturbed system (α = k, τ, ± where ± indicate the valence and conduction bands, respectively) and setting  or
or  we have
we have  with ψf the wavefunction of the final photo-electron state and
with ψf the wavefunction of the final photo-electron state and  —the choice of parametrization for the probe polarization allows for the use of symmetry arguments to determine ψf16. These matrix elements are given in terms of the dipole transition matrix elements
—the choice of parametrization for the probe polarization allows for the use of symmetry arguments to determine ψf16. These matrix elements are given in terms of the dipole transition matrix elements  and
and  for the x and y components of the probe pulse respectively (see Supplementary Information). In the expressions above, |kA〉 and |kB〉 are the Bloch wavefunctions of the A and B sublattices, respectively.
for the x and y components of the probe pulse respectively (see Supplementary Information). In the expressions above, |kA〉 and |kB〉 are the Bloch wavefunctions of the A and B sublattices, respectively.
Recent experiments16 showed that for graphene the ratio ζy/ζx = λeiβ depends on the frequency of the photo-emitting probe pulse: λ is on the order of one and  while for high energies (~30 eV) while
while for high energies (~30 eV) while  for lower energies (~20 eV). It is worth to emphasize that these particular values of β depend on the final state ψf and hence on the choice of symmetry of the polarization of the probe pulse, whose principal axes are always along the x and y directions. In the former case the momentum distribution of the photo-electrons gives valuable information on the Berry phase and has been analyzed in detail in ref. 16 and in subsequent works in the absence of the pump perturbation34,35. In this case a simple calculation gives the following photo-electron distribution due to electrons with quantum numbers k, τ, ±,
for lower energies (~20 eV). It is worth to emphasize that these particular values of β depend on the final state ψf and hence on the choice of symmetry of the polarization of the probe pulse, whose principal axes are always along the x and y directions. In the former case the momentum distribution of the photo-electrons gives valuable information on the Berry phase and has been analyzed in detail in ref. 16 and in subsequent works in the absence of the pump perturbation34,35. In this case a simple calculation gives the following photo-electron distribution due to electrons with quantum numbers k, τ, ±,

with θk = arctan(ky/kx).
Photons with different polarization selectively excite electrons in the BZ generating a marked dichroism. This is reflected in the angular dependence of constant energy maps of  close to the K point. The angular dependence of the photo-electron distribution highlights the chiral nature of the initial states and gives direct information of the winding phase θk. Similar results are obtained with a pump pulse as shown in Fig. 1(d). To lowest order in the pump amplitude, the photo-electron intensities are given by Eq. (7) where now Δ is to be replaced by
close to the K point. The angular dependence of the photo-electron distribution highlights the chiral nature of the initial states and gives direct information of the winding phase θk. Similar results are obtained with a pump pulse as shown in Fig. 1(d). To lowest order in the pump amplitude, the photo-electron intensities are given by Eq. (7) where now Δ is to be replaced by  . Then the pump changes the band structure as suggested by the lowest order Floquet Hamiltonian [cf. Eq. (2)] and the closing of the mass gap at K can be observed. However, under these conditions (
. Then the pump changes the band structure as suggested by the lowest order Floquet Hamiltonian [cf. Eq. (2)] and the closing of the mass gap at K can be observed. However, under these conditions ( ) the ARPES spectrum cannot distinguish the two different topological phases. In fact, the β = 0 photo-electron distribution
) the ARPES spectrum cannot distinguish the two different topological phases. In fact, the β = 0 photo-electron distribution  is independent of the sign of the mass term, which means that the intensity pattern remains invariant under a change in the orientation of the pseudo-spin along the z axis. In this case, although the ARPES can detect the closing and reopening of the gap at one of the Dirac points as the amplitude of the pump pulse increases, this cannot be unambiguously assigned to a band inversion. In particular, in graphene where Δ = 0 the gaps at the two Dirac point are identical and the photo-electron intensities are insensitive to the sign of
is independent of the sign of the mass term, which means that the intensity pattern remains invariant under a change in the orientation of the pseudo-spin along the z axis. In this case, although the ARPES can detect the closing and reopening of the gap at one of the Dirac points as the amplitude of the pump pulse increases, this cannot be unambiguously assigned to a band inversion. In particular, in graphene where Δ = 0 the gaps at the two Dirac point are identical and the photo-electron intensities are insensitive to the sign of  .
.
However, when  , a situation experimentally observed for
, a situation experimentally observed for  , the ARPES spectrum changes at the critical amplitude of the pump pulse allowing for a clear identification of the topology of the Floquet bands. Before presenting the numerical results we may get some insight into the problem by evaluating the photo-electron distribution using again the lowest order Floquet Hamiltonian. For λ = 1 and β = π/2 this approach gives
, the ARPES spectrum changes at the critical amplitude of the pump pulse allowing for a clear identification of the topology of the Floquet bands. Before presenting the numerical results we may get some insight into the problem by evaluating the photo-electron distribution using again the lowest order Floquet Hamiltonian. For λ = 1 and β = π/2 this approach gives

with  and
and  . This simple result makes apparent that the ARPES spectrum for non-linear polarization of the probe (χ ≠ 0 or π/2) depends on the sign of the mass term. Consequently, the topological transition is manifested as a change in the amplitude of the photo-electron intensities showing different behaviors at the K and K′ cones. Under this choice of parameters it is possible to generate a photo-electron distribution with purely A or B character, i.e. to selectively photo-emit states with different pseudo-spin polarization along the z axis. Equation (8) also shows that the dichroism depends on the helicity of the probe. Defining the dichroism factor D as the normalized maximum angular variation of the photoemission intensity along a constant energy curve we obtain
. This simple result makes apparent that the ARPES spectrum for non-linear polarization of the probe (χ ≠ 0 or π/2) depends on the sign of the mass term. Consequently, the topological transition is manifested as a change in the amplitude of the photo-electron intensities showing different behaviors at the K and K′ cones. Under this choice of parameters it is possible to generate a photo-electron distribution with purely A or B character, i.e. to selectively photo-emit states with different pseudo-spin polarization along the z axis. Equation (8) also shows that the dichroism depends on the helicity of the probe. Defining the dichroism factor D as the normalized maximum angular variation of the photoemission intensity along a constant energy curve we obtain  . For a circularly polarized probe pulse (χ = π/4) we have that D± = 0 and the information on the Berry phase is lost—the constant energy cuts of the photo-electron distribution are angle independent. However, the intensity of the photocurrent coming from the valence and conduction bands clearly shows the topological structure of the wavefunctions,
. For a circularly polarized probe pulse (χ = π/4) we have that D± = 0 and the information on the Berry phase is lost—the constant energy cuts of the photo-electron distribution are angle independent. However, the intensity of the photocurrent coming from the valence and conduction bands clearly shows the topological structure of the wavefunctions,

This is shown in Fig. 2 where the numerical simulation with the full time dependence of the pump and probe pulses are presented. The figure was obtained by fixing the chemical potential at a high energy (high doping) in order to show the photo-electron intensities corresponding to the valence and conduction bands in a wide energy range. The circularly polarized probe pulse acts at the centre of the pump pulse and its width in the time domain was chosen to be δtprobe = 50 fs to have a good energy resolution of the Floquet bands. The results clearly show that near the K point, the maximum intensity of the photo-electron distribution changes from the conduction to the valence band at the critical amplitude Ac. This change is a consequence of the sign change of  and is linked to a change of
and is linked to a change of  .
.
(a) ARPES intensity from states close to the K′ (left column) and K (right column) cones; the radiation intensity increases from top to bottom (field strength (evFA0) at the peak of the pump pulse of 0 meV, 60 meV, 130 meV and 200 meV). These results correspond to a circularly polarized pump and probe pulses with β = π/2, the temporal duration of the former being of 350 fs and the latter of δtprobe = 50 fs. The chemical potential has been taken at 0.5 eV to appreciate the intensity changes of photo-electrons from both the valence and the conduction bands. The pump energy is ħΩ = 400 meV. In (b) we show the intensities, from states with wavevector k slightly shifted from the Dirac points, as function of the radiation intensity. At the critical value of evFA0 = 130 meV the ARPES intensity around K is transferred from the conduction to the valence band.
To be more specific, we now present results for the case of graphene with realistic parameters. We used the experimentally observed value of the phase β = 0.4π, the chemical potential is set either at μ = 100 meV or μ = 0 meV, the frequency of the pump pulse is ħΩ = 400 meV and the probe pulse is circularly polarized. These conditions generate small dichroism although its symmetry is different from that observed with β = 0: note that in cuts along ky and in the absence of the pump pulse the lines with negative velocity in Fig. 3(a) are more intense around both the K and K′ points. The circularly polarized pump pulse with frequency Ω also opens gaps at the Floquet zone boundary (ħΩ/2) that are detected by the ARPES spectrum14. The second order gap at the zone centre (zero energy) is not clearly observed due to the moderate amplitude of the pump and the width of the ARPES lines. However, the intensities of the lines corresponding to the conduction band show a marked different behavior at the two Dirac points as illustrated in Fig. 3(c). This behavior shows that the Berry curvature Ωkτ defined above has the same sign for the two cones leading to a non-zero Chern number. This effect is also present when the chemical potential is fixed at μ = 0 eV as shown in Fig. 3(d), where the photoemission spectrum is presented along the kx direction in order to disregard asymmetries due to the dichroism generated by the probe polarization.
ARPES intensity for graphene (Δ = 0) and β = 0.4π corresponding to a probe photon of 20 eV.The pump and probe pulses are circularly polarized, the former with a time domain width of 250 fs and the latter with 20 fs. In all panels the left (right) column corresponds to the K′ (K) cone. (a) Cuts of the ARPES intensity along ky for graphene in equilibrium (no pump pulse, upper panels) and irradiated graphene (wtih a pump pulse, lower panels) around the Dirac points. (b) Constant energy cuts at 100 meV (CB) and at −100 meV (VB). Note the small dichroism obtained with β = 0.4π. Contrary to the case of linearly polarized probe, now the dichroism around K and K′ has the same symmetry. (c) Intensity of the valence band photo-electrons along kx from states close to each valley. The maximum at K′ and the minimum at K signals the non trivial topology of the Bloch wavefunctions of this band. (d) Cuts of the photoemission spectrum for graphene along kx with chemical potential fixed at μ = 0 eV in equilibrium (upper panels) and irradiated (lower pannels) near–the Dirac points.
In finite systems, the Floquet zone boundary gaps are also bridged by topologically protected edge states. In k-space, these edge states are confined arround the K and K′ points and their existence can be inferred by evaluating the Chern numbers with the Floquet bands20,22,36. The wavefunctions in the time domain clearly show that for those states bridging the zone-boundary gap the pseudospin oscillates with frequency Ω with its time average value on the xy-plane. The topological structure of these states, described by the above mentioned Chern numbers, is a real dynamical effect37. As the ARPES probe pulse averages on a time scale of the order of δtprobe ≫ 1/Ω, the photo-electrons can hardly carry some information on the topological nature of states at the zone-boundary gap.
It is worth mentioning that, as recently shown in ref. 38, the Chern number of a pure state (Slater determinant) cannot be changed by a unitary transformation. That is, the Chern of an initial state remains unaltered during the pump pulse. This fact of course does not prevent modifications of the band structure, the Floquet spectrum, and in particular the presence of the band inversion phenomena. In ARPES experiments with the appropriate energy and polarization, the interference of the dipole transitions allows for a clear identification of the different topological phases as revealed by the band inversion effect. With the help of a band structure model, that for graphene is well established, the ARPES intensity profiles allows to determine amplitude and phases of the wavefunctions for states close to the K and K′ points of the BZ and to reconstruct the Berry curvature around these hot spots.
The case of bilayer graphene, with a rather different band structure, is also interesting. The system has four π-bands, two of them, with parabolic dispersions, touch each other at the Dirac points and a gap can be opened and controlled by a perpendicular electric field. The other two bands lie at about 0.3 eV from the Dirac points. In the presence of the pump pulse these extra bands generate Floquet replicas that partially cover up the low energy ARPES spectrum making it much more intricate. Nevertheless, as the pump amplitude increases the topological transition evidenced by the band inversion phenomena can be clearly observed (see Supplementary Information).
In summary, we have shown that ARPES can give clear information on the topology of Floquet bands of graphene and graphene-like structures. This information is given by the intensity of the ARPES profiles of the bands close to the K and K′ points of the BZ. While in the topological trivial phase the intensities due to photo-electrons from the valence or conduction bands are similar at the two Dirac points, in the non-trivial phase the intensities of the valence and conduction bands are different and opposite at K and K′. This change signals a modification of the Berry curvature around these points with a consequent variation of the Chern numbers. To observe the effect the dipole transition matrix elements ζx and ζy should have a different phase β. It has been experimentally shown that in graphene β can be controlled with the photon energy of the probe pulse. This observation opens the road for a spectroscopic study of the topological properties of the bulk wavefunctions of these 2D materials.
Additional Information
How to cite this article: Gavensky, L. P. et al. Photo-electrons unveil topological transitions in graphene-like systems. Sci. Rep. 6, 36577; doi: 10.1038/srep36577 (2016).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
M. Z. Hasan & C. L. Kane . “Colloquium: Topological insulators”. Rev. Mod. Phys. 82, 3045 (2010).
Y. Ando . “Topological insulator materials”. J. Phys. Soc. Jpn. 82, 102001, http://dx.doi.org/10.7566/JPSJ.82.102001 (2013).
B. A. Bernevig & T. L. Hughes . Topological Insulators and Topological Superconductors (Princeton University Press, 2013).
S.-Q. Shen . Topological Insulators: Dirac Equation in Condensed Matters, 2013th ed., Springer Series in Solid-State Sciences (Book 174) (Springer, 2013).
D. Xiao, M.-C. Chang & Q. Niu . “Berry phase effects on electronic properties”. Rev. Mod. 82, 1959 (2010).
M. König et al. “Quantum spin hall insulator state in hgte quantum wells”. Science 318, 766 (2007).
D. Hsieh et al. “A topological dirac insulator in a quantum spin hall phase”. Nature 452, 970 (2008).
J. Karch et al. “Terahertz radiation driven chiral edge currents in graphene”. Phys. Rev. Lett. 107, 276601 (2011).
K. Kristinsson, S. Kibis, O. Vand Morina & I. A. Shelykh . “Control of electronic transport in graphene by electromagnetic dressing” Sci. Rep. 6, 20082 (2016).
M.-C. Chang & Q. Niu . “Berry phase, hyperorbits, and the hofstadter spectrum”. Phys. Rev. Lett. 75, 1348 (1995).
G. Sundaram & Q. Niu . “Wave-packet dynamics in slowly perturbed crystals: Gradient corrections and berry-phase effects”. Phys. Rev. B 59, 14915 (1999).
L. Tarruell, D. Greif, T. Uehlinger, G. Jotzu & T. Esslinger . “Creating, moving and merging dirac points with a fermi gas in a tunable honeycomb lattice”. Nature 483, 302 (2012).
L. Duca et al. “An aharonov-bohm interferometer for determining bloch band topology”. Science 347, 288 http://www.sciencemag.org/content/347/6219/288.full.pdf (2015).
Y. H. Wang, H. Steinberg, P. Jarillo-Herrero & N. Gedik . “Observation of floquet-bloch states on the surface of a topological insulator”. Science 342, 453 (2013).
F. Mahmood et al. Selective scattering between floquet-bloch and volkov states in a topological insulator”. Nat Phys 12, 306 (2016).
Y. Liu, G. Bian, T. Miller & T.-C. Chiang . “Visualizing electronic chirality and berry phases in graphene systems using photoemission with circularly polarized light”. Phys. Rev. Lett. 107, 10.1103/physrevlett.107.166803 (2011).
T. Oka & H. Aoki . “Photovoltaic hall effect in graphene”. Phys. Rev. B 79, 081406 (2009).
T. Kitagawa, E. Berg, M. Rudner & E. Demler . “Topological characterization of periodically driven quantum systems”. Phys. Rev. B 82, 235114 (2010).
N. H. Lindner, G. Refael & V. Galitski . “Floquet topological insulator in semiconductor quantum wells”. Nat. Phys. 7, 490 (2011).
M. S. Rudner, N. H. Lindner, E. Berg & M. Levin . “Anomalous edge states and the bulk-edge correspondence for periodically-driven two dimensional systems”. Phys. Rev. X 3, 031005 (2013).
P. M. Perez-Piskunow, G. Usaj, C. A. Balseiro & L. E. F. Foa Torres . “Floquet chiral edge states in graphene”. Phys. Rev. B 89, 121401(R) (2014).
G. Usaj, P. M. Perez-Piskunow, L. E. F. Foa Torres & C. A. Balseiro . “Irradiated graphene as a tunable floquet topological insulator”. Phys. Rev. B 90, 115423 (2014).
M. Ezawa . “A topological insulator and helical zero mode in silicene under an inhomogeneous electric field”. New Journal of Physics 14, 033003 (2012).
T. Wehling, A. Black-Schaffer & A. Balatsky . “Dirac materials”. Advances in Physics 63, 1, http://dx.doi.org/10.1080/00018732.2014.927109 (2014).
J. Shirley . “Solution of the schrödinger equation with a hamiltonian periodic in time”. Phys. Rev. 138, B979 (1965).
H. Sambe . “Steady states and quasienergies of a quantum-mechanical system in an oscillating field”. Phys. Rev. A 7, 2203 (1973).
M. Grifoni & P. Hänggi . “Driven quantum tunneling”. Phys. Rep. 304, 229 (1998).
S. Kohler, J. Lehmann & P. Hänggi . “Driven quantum transport on the nanoscale”. Phys. Rep. 406, 379 (2005).
M. Ezawa . “Photoinduced topological phase transition and a single dirac-cone state in silicene”. Phys. Rev. Lett. 110, 026603 (2013).
X. Zhai & G. Jin . “Photoinduced topological phase transition in epitaxial graphene”. Phys. Rev. B 89, 235416 (2014).
M. Ezawa . “Monolayer topological insulators: Silicene, germanene and stanene”. 1503.08914 (2015).
J. Braun, R. Rausch, M. Potthoff, J. Minár & H. Ebert . One-step theory of pump-probe photoemission. Phys. Rev. B 91, 035119 (2015).
M. A. Sentef et al. “Theory of floquet band formation and local pseudospin textures in pump-probe photoemission of graphene”. Nature Comm. 6, 7047 (2015).
C. Hwang . “Angle-resolved photoemission spectroscopy study on graphene using circularly polarized light”. Journal of Physics: Condensed Matter 26, 335501 (2014).
H. Hwang & C. Hwang . “Tight-binding approach to understand photoelectron intensity from graphene for circularly polarized light”. Journal of Electron Spectroscopy and Related Phenomena 198, 1 (2015).
P. M. Perez-Piskunow, L. E. F. Foa Torres & G. Usaj . “Hierarchy of floquet gaps and edge states for driven honeycomb lattices”. Phys. Rev. A 91, 043625 (2015).
L. E. F. Foa Torres, P. M. Perez-Piskunow, C. A. Balseiro & G. Usaj . “Multiterminal conductance of a floquet topological insulator”. Phys. Rev. Lett. 113, 266801 (2014).
L. D’ Alessio & M. Rigol . “Dynamical preparation of floquet chern insulators”. Nat Commun 6, 10.1038/ncomms9336, note article (2015).
Acknowledgements
We acknowledge financial support from PICTs 2013-1045 and Bicentenario 2010-1060 from ANPCyT, PIP 11220110100832 from CONICET and grant 06/C415 from SeCyT-UNC. GU acknowledges support from the ICTP associateship program and thanks the Simons Foundation.
Author information
Authors and Affiliations
Contributions
L.P.G. carried out the numerical simulations and analytical calulations. All authors contributed to the discussion and wrote the manuscript text.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Peralta Gavensky, L., Usaj, G. & Balseiro, C. Photo-electrons unveil topological transitions in graphene-like systems. Sci Rep 6, 36577 (2016). https://doi.org/10.1038/srep36577
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep36577
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.