Abstract
Recent progress in laser wakefield acceleration has led to the emergence of a new generation of electron and X-ray sources that may have enormous benefits for ultrafast science. These novel sources promise to become indispensable tools for the investigation of structural dynamics on the femtosecond time scale, with spatial resolution on the atomic scale. Here, we demonstrate the use of laser-wakefield-accelerated electron bunches for time-resolved electron diffraction measurements of the structural dynamics of single-crystal silicon nano-membranes pumped by an ultrafast laser pulse. In our proof-of-concept study, we resolve the silicon lattice dynamics on a picosecond time scale by deflecting the momentum-time correlated electrons in the diffraction peaks with a static magnetic field to obtain the time-dependent diffraction efficiency. Further improvements may lead to femtosecond temporal resolution, with negligible pump-probe jitter being possible with future laser-wakefield-accelerator ultrafast-electron-diffraction schemes.
Similar content being viewed by others
Introduction
After decades of development, electron diffraction and microscopy have become robust and powerful techniques for determining material structure at equilibrium with atomic-scale resolution. Following the availability of femtosecond lasers in the 1980s, a number of ultrafast time-resolved techniques have been developed to study the dynamics of atomic, molecular, and condensed systems on femto- to picosecond time scales. Combining ultrafast temporal resolution with ultrahigh spatial resolution, short pulses of X-rays or electrons have the unique capability for direct structural visualisation at the atomic-level. Ultrafast X-ray pulses with durations on the order of 100 fs can currently be produced at large-scale accelerator facilities such as synchrotrons using slicing schemes1,2 or through the use of free-electron lasers3. On the other hand, producing electron pulses can be achieved using a relatively compact setup at university-scale laboratories. Compared to X-ray photons, electrons have a much higher elastic scattering cross-section and have a sub-atomic de Broglie wavelength, which makes them ideal probes for thin solid samples, gas phase, and nanoscale systems4,5.
Conventional ultrafast electron diffraction techniques use DC photoguns to accelerate electrons to non-relativistic energies in the 30–100 keV range, where the space-charge effect (Coulomb repulsion) has been a major limitation to the ultimate temporal resolution. In the past decade, research toward increasing the temporal resolution has been very active, with the motivation of being able to observe the fastest structural changes that can occur in materials. Several methods have been developed, including ultra-compact electron gun designs6, space-charge free bunches using single- or few-electron-pulses7,8,9 and radio-frequency (RF) cavities for recompressing the electron bunches10,11,12. RF guns producing MeV electrons have also been used successfully for ultrafast electron diffraction13,14,15, with electron bunches containing more charge thanks to the reduction of space-charge at higher energy. However, despite this progress, reaching resolution shorter than 100 fs has been difficult, either because of the jitter of the RF source11,12,14 or because of the intrinsic limitations of the photoemission process at the photocathode7.
Recent advances in high-intensity laser development have opened up a new range of laser-plasma based X-ray and electron sources. X-rays produced in solid-density plasmas16 have been widely used for time-resolved X-ray diffraction with sub-picosecond resolution for almost two decades17. Laser intensities exceeding 1018 W/cm2 can now be routinely delivered by table-top laser systems, enabling remarkable progress in Laser Wakefield Acceleration of electron bunches with energies ranging up to multi-GeV18,19. In a laser wakefield accelerator, an ultra-intense laser pulse is focused into a plasma and excites a large amplitude plasma wave, the so-called wakefield, in which electrons can be trapped and accelerated to high energies. This technique provides acceleration gradients orders of magnitude higher than their conventional counterparts based on RF technologies, so that electrons reach MeV energies in tens of microns only, therefore providing very compact sources of electrons and also photons20. When the injection and acceleration processes are controlled properly, electron bunches can be generated with sub-10 fs duration21 that are intrinsically synchronised to the femtosecond laser system. Laser wakefield accelerators consequently also have great potential as all-optical sources for near jitter-free time-resolved measurements22. In particular, ultrafast electron diffraction measurements using laser wakefield accelerated electrons could benefit from all these advantages.
In our study, we make use of the ultrashort bunch duration of laser wakefield accelerated electrons to perform time-resolved electron diffraction measurements of the structural dynamics of single-crystal silicon nano-membranes in an all-optical pump-probe arrangement. While solid density plasmas23,24 or direct laser acceleration using radially polarised light25,26 have been proposed as sources for ultrafast electron diffraction, to our knowledge no time-resolved electron diffraction experiments have previously been performed using a laser-plasma source. Our measurements were made possible by the development of a laser wakefield accelerator operating at kHz repetition rate with superior stability, delivering electrons in the 100 keV range27,28, with the transverse coherence required for electron diffraction29 along with dramatic beam quality improvements enabled by active feedback control30.
Using a laser wakefield accelerator has the advantage of achieving a near jitter-free pump-probe synchronisation and producing electron bunches with uncorrelated initial durations at the few-femtosecond level. In our experiment, the emitted electrons have a significant energy spread (ΔE/E = 10–20%), which results in significant bunch elongation during propagation. However, as the beam drifts in free space, it develops a well defined linear energy chirp in the longitudinal phase-space, i.e., a momentum-position correlation. Therefore, in this work we performed the time-resolved measurements with the elongated electron pulse, which is diffracted off the sample and subsequently streaked by a static magnetic field, thereby transforming temporal information to a spatial diagnostic31,32,33,34. This mode of operation allows experimentalists to capture the entire time history in a single image without the need to scan different time delays as in the traditional stroboscopic mode. Although our measurements have a diagnostic-limited picosecond resolution, it is clear that 100s or even 10s femtosecond resolution may be possible with further development.
Results
Experimental set-up
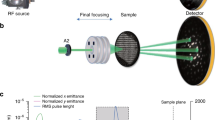
Figure 1 shows a schematic of the experimental setup. Laser pulses with 35 fs duration at full-width-at-half-maximum (FWHM) and energies of 15 mJ were focussed to intensities of 2–3 × 1018 W/cm2 (see Methods) into a continuously flowing gas target to generate electron bursts having energies around 100 keV at 0.5 kHz via laser wakefield acceleration27. Using a feedback loop to control the laser wavefront30, the electron beam was optimised in terms of divergence and beam charge such that the total charge reached 50 fC (about 300 000 electrons). Only a fraction (between 10–15 per cent) of the electrons were delivered to the sample after being emittance-filtered by a pinhole and collimated with a solenoid magnetic lens. The electron bunch measured at 35 cm from the gas target had a spot size of 0.5 mm vertically and 0.7 mm horizontally at half-maximum. At the specimen plane (d = 13.5 cm from the source), the transverse size of the electron beam was estimated to match the size of the Si samples, i.e. less than 350 μm (see Methods). The chirped bunch duration at the sample position can be estimated to be  , giving
, giving  ps for a 100 keV electron bunch with a 20% energy spread. For streaking the electron bunch, a horizontal slit was used to select the zero-order and the (220) spots diffracted in the horizontal plane. Electrons in the selected peaks then entered a magnetic deflection region and were streaked vertically along the y−axis by the static magnetic field (see Fig. 1).
ps for a 100 keV electron bunch with a 20% energy spread. For streaking the electron bunch, a horizontal slit was used to select the zero-order and the (220) spots diffracted in the horizontal plane. Electrons in the selected peaks then entered a magnetic deflection region and were streaked vertically along the y−axis by the static magnetic field (see Fig. 1).
Experimental layout of streaked time-resolved electron diffraction.
A 15-mJ Ti:Sapphire laser system is used for generating both the electron probe and the optical pump on the sample. Approximately 10 mJ of the 800 nm laser pulse energy is focussed into an argon gas jet produced by a 100 μm capillary nozzle for generating bursts of electrons. The remaining fraction of the beam is frequency doubled to 400 nm and delivered to the sample for optical excitation at an absorbed fluence of 1–2 mJ/cm2. The electron beam is filtered by a 280 μm aperture before entering a solenoidal magnetic lens. A 30 nm thick single-crystal silicon sample is placed at d = 13.5 cm from the electron source. An optical micrograph of the array of si nano-membranes and supporting grid is displayed. The diffracted electrons enter a horizontal slit before they are spatially dispersed onto a detector screen via a pair of dipole magnets.
For optical excitation, the 30 nm single-crystal silicon sample was pumped by 400 nm s-polarised pulses at an incident angle of θ = 20°. The pump beam size was set slightly larger than the electron probed area to ensure spatial pump-probe overlap. The absorbed pump fluence in our experiment was in the range 1–2 mJ cm−2.
Temporal characterisation of the laser-plasma accelerated source
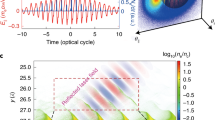
The time delay between the optical pump and electron probe was determined by focussing the near-infrared optical beam onto the tip of a tungsten needle target at the sample plane. The pump pulse is able to field-ionize electrons from the needle surface, thereby creating charge separation fields that cause a local deflection of the electron beam and modify the beam intensity on the detector. Therefore, the arrival of the optical pump is encoded in the streaked electron beam and can be measured by subtracting the pumped (I0) and unpumped pattern (I1), I1−I0, see Fig. 2b. By changing the position of the delay line, one can scan the arrival of the pump pulse through the streak pattern, thereby providing a direct calibration converting the spatial position of a streak to an axis of time, see Fig. 2c.
Delay time calibration using a tungsten needle target (a) Schematic of experimental setup for the calibration of the pump-probe delay. (b) Intensity lineout profile I1−I0 along y axis (streaking direction) showing the effect of the pump pulse on the needle. (c) Delay time plotted as a function of the position of the signal measured at location d = 13.5 cm and d = 1.9 cm. Horizontal error bars represent the signal transition width from 10% to 90% of the peak.
Once the delay line is set, there is no further need for scanning and Fig. 2c shows that the chirped electron beam provides a temporal window of 120 ps when the sample is placed at d = 13.5 cm. Figure 2b also shows that the decay time of the signal is 7 ps, which sets an upper limit to the temporal resolution of this particular configuration. This is limited by the magnetic-deflection diagnostic, not the inherent slice-duration of the electron beam. The pump-probe data in our experiments were taken at d = 13.5 cm in order to benefit from a larger temporal window and also to keep the fluence of the main laser beam onto the Si sample at an acceptably low level.
To demonstrate that this set-up is not limited by the electron source but the magnetic-deflection diagnostic, we also placed the target closer to the source at d = 1.9 cm. By doing so, the resolution can be significantly enhanced. The lower panel of Fig. 2c, which was taken with d = 1.9 cm, shows the temporal window is only about 15 ps because the electron bunch duration is shorter at this point but the upper limit on the resolution is now hundreds of femtoseconds.
Lattice dynamics of the silicon nano-membranes
The quality of the single-crystal silicon membranes and their thickness of only 30 nm (see Methods) allowed us to obtain high-quality diffraction images. Figure 3a shows a diffraction pattern of the [001] oriented Si sample. The energy spread of the electron beam leads to radial broadening of the Bragg peaks, which becomes more apparent at higher diffraction orders. Sending the pump beam causes photo-induced changes to the diffraction pattern which are easily measured by probing the sample at 300 ps after the arrival of the pump pulse. Figure 3b was obtained by subtracting the pump diffraction pattern from the unpumped pattern. The relative changes of the central undiffracted (0-order) spot and (220) Bragg peaks are shown in Fig. 3c. The dynamics associated with the four (220) diffraction peaks showed dissimilar trends, featuring an increase of diffraction efficiency for some (220) spots, such as spot 2 which increases by more than 10% in Fig. 3(b,c). Similar results on Si membranes were observed in ref. 35.
Diffraction pattern and pump-probe signal without streaking (a) Diffraction pattern of single crystalline silicon, unpumped (accumulated for 200 shots). (b) Subtracted signal of the pumped and unpumped diffraction data I1 − I0 averaged over 30 pump-probe cycles. The pump-probe delay is 300 ps time delay and the absorbed fluence is 1.9 mJ/cm2. (c) Relative signal change for the undiffracted spot and four (220)-order Bragg spots I1/I0 − 1. Error bars, 95% confidence interval.
We may draw a few conclusions from Fig. 3. First, because some of the peaks increase in brightness, the photo-induced response cannot be explained simply by lattice heating and the Debye-Waller effect, which always reduce the intensity of all the Bragg peaks. Second, our observation cannot be explained by a change of the structure factor, i.e., the positions of atoms in the unit cell. Indeed, it is readily seen that the structure factor for the (220) silicon peaks is maximum, i.e., each atom in the unit cell contributes to the maximum constructive interference.
Reference 35 suggests that the increase of the Bragg peak intensity might originate from thermoelastic deformation of the crystal. In this scenario, electrons are first excited to high-energy states and then subsequently relax to the bottom of the conduction band while emitting phonons and causing ultrafast heating of the Si lattice on picosecond time scales36. The key point is that the heating is non-uniform (as it follows the transverse distribution of the pump pulse), which in conjunction with the fixed boundary conditions imposed by the support grid structure, results in a thermal strain as well as surface bulging35. These effects could effectively alter the angles of the (220) planes, leading to changes in the diffracted intensity. In particular, this scenario is compatible with our experimental results as it can account for increasing Bragg peaks: a (220) peak which is initially slightly off Bragg could fully satisfy the Bragg condition after photo-excitation, explaining the increase in signal.
We now investigate the ultrafast dynamics by streaking the Bragg peaks. Results from two data sets are presented in Fig. 4 for ultrafast dynamics of the undiffracted (0-order) and one of the (220)-order peaks. The pump beam profile and fluence used for both data sets were similar with an absorbed fluence of 1.3 mJ/cm2. At this fluence level, the density of excited carriers is approximately 1021 cm−3, i.e. 0.5% of the valence electrons are excited to the conduction band. For data set I shown in Fig. 4(a–c), a decrease of the (220) Bragg peak intensity was observed on a few picosecond time scale, followed by a metastable state lasting more than a 100 ps. As the 0-order was saturated in this data set, we focused on the dynamics of the 0-order in data set II. In this case, no significant dynamics was observed for the selected (220) peak (Fig. 4e) while the 0-order diffraction spot shows a ~12% decrease [Fig. 4(f–g)] on a similar time scale. We attribute the different behaviour of the (220) peak in the two data sets to slightly different initial sample orientations (<1°).
Time-resolved dynamics with streaked electron diffraction.
Time-resolved streak signal from two different sets of data for the (220)-order and the undiffracted (0-order) spot respectively. Panel (a) raw averaged data showing the unpumped (I0, upper panel) and pumped (I1, middle panel) signal of the streaked (220) Bragg peak. The bottom panel represents the relative change of the diffraction peak I1/I0−1. (b) Relative change of the (220) peak obtained by transverse integration along x. (c) shows the (220) Bragg peak dynamics measured under similar conditions using a conventional DC electron gun. Panels (d–f) data from another set of measurements where the crystalline sample was tilted at a slightly different angle. (d) shows that in this case, the relative changes are larger for the 0-order spot. (e) Relative change of the 0-order. (f) Dynamics of the 0-order obtained using the conventional DC gun. Solid lines (red) are fits to the data with the decay time constants and the standard errors displayed. Vertical error bars (light blue) in (b) and (e), 95% confidence interval.
For comparison, we have also performed pump-probe experiments using a conventional DC electron gun in the stroboscopic mode, i.e., a diffraction image is collected for each pump-probe delay (see Methods). The curves for the (220) spot and 0-order dynamics are plotted in Fig. 4(c,f) respectively. The transients have similar features as in data sets I and II obtained with the plasma source: decay time in the ps range followed by a plateau lasting more than a 100 ps. The change in Bragg peak intensity is larger because the absorbed fluence was higher: 3.5 mJ/cm2. The discrepancy between the two data sets was also reproduced: data set II (Fig. 4(f)) was obtained by tilting the sample by 0.8° confirming the sensitivity of the photo-induced response to the initial orientation of the sample.
Finally, the measured data points are fitted by an exponential decay function convolved with a Gaussian instrumental response, e.g., 7 ps FWHM for the laser-plasma source (instrument limited) 3.1 ± 0.8 ps and 3.0 ± 0.2 ps for the conventional source. This further confirms that the laser-plasma source is able to resolve the ultrafast dynamics of the Si lattice.
All these observations can be explained as follows: first, electron-phonon coupling governs the changes of the lattice during the first few picoseconds, explaining the few picosecond drop of the (220) Bragg peak intensity. Second, electron-hole pair recombination occurs through Auger recombination. At this high density of excited carriers, 1021 cm−3, screening of the electron-hole plasma mitigates the Auger recombination rate, as seen in experiments37 and theoretical work38. Therefore, it is likely that recombination occurs on time scales longer than 100 ps, explaining the longevity of the metastable excited state, which lasts more than 100 ps in our data.
Discussion
The previous measurements confirm that laser-plasma accelerators can deliver an electron beam with sufficient quality and stability in order to probe structural dynamics at the picosecond level. We now address the question of the limits of our streaking method.
The overall temporal resolution can be estimated as  , where
, where  fs (FWHM) is the pulse duration of the pump laser pulse, τuncorr is the uncorrelated electron bunch duration at the source (simulations27,28 predict that τuncorr < 100 fs), τjitter is the overall timing jitter in the laser-plasma accelerator and τangle comes from the non-collinear geometry between pump and probe:
fs (FWHM) is the pulse duration of the pump laser pulse, τuncorr is the uncorrelated electron bunch duration at the source (simulations27,28 predict that τuncorr < 100 fs), τjitter is the overall timing jitter in the laser-plasma accelerator and τangle comes from the non-collinear geometry between pump and probe:  fs in our case. As the electron injection and acceleration mechanisms in plasma waves rely on a deterministic evolution of plasma dynamics30 rather than a stochastic process, it is unlikely to induce any significant temporal jitter at the electron emission. Most importantly, τstreak is the temporal resolution depending on the specific streaking geometry. Clearly, the last term dominates our observed temporal resolution in the experiment, which is limited by the transverse electron spot size and the geometry of the streaking, subject to the space constraint of the vacuum chamber.
fs in our case. As the electron injection and acceleration mechanisms in plasma waves rely on a deterministic evolution of plasma dynamics30 rather than a stochastic process, it is unlikely to induce any significant temporal jitter at the electron emission. Most importantly, τstreak is the temporal resolution depending on the specific streaking geometry. Clearly, the last term dominates our observed temporal resolution in the experiment, which is limited by the transverse electron spot size and the geometry of the streaking, subject to the space constraint of the vacuum chamber.
If δE is the energy resolution at E for the streaking spectrometer and consider on-axis electrons, τstreak is the time-of-flight difference for electrons of E − δE/2 and E + δE/2 over a distance of d from their source to the sample:

where vz is the longitudinal velocity and the term  comes from the relativistic correction factor. Substituting in the values from our silicon pump-probe experiment (d = 13.5 cm, δE = 1.6 keV, E = 90 keV) resulted in τstreak = 6.0 ps (evaluated near the time zero), in agreement with the measured resolution.
comes from the relativistic correction factor. Substituting in the values from our silicon pump-probe experiment (d = 13.5 cm, δE = 1.6 keV, E = 90 keV) resulted in τstreak = 6.0 ps (evaluated near the time zero), in agreement with the measured resolution.
There is no physical limit for reducing τstreak to the same level of τuncorr and τjitter, which may be on the order of 10 fs. As can be seen from equation (1), further improvement on the temporal resolution is straightforward by increasing the streaking strength (i. e., decreasing δE), at the cost of either lower signal-to-noise ratio or longer acquisition time. Another way to increase the temporal resolution is to reduce d, the source to sample distance. As shown before with the delay calibration using the needle target, d = 1.9 cm yields a τstreak of 0.84 ps, under identical streaking conditions. One potential issue with decreasing d comes from the fact that the co-propagating laser radiation used to drive electron acceleration might be too intense for the sample and needs to be blocked or reflected while allowing the electron beams to pass. Finally, another way to decrease τstreak is to increase the electron energy E while keeping the resolution of the magnetic spectrometer the same. This may become possible in the near future with recent results showing that multi-MeV electrons can be generated39,40.
Stability of the laser-plasma electron source is the main challenge in our experiments. Shot-to-shot noise (fluctuation in the unpumped data) near the central part of a streak typically has a signal-to-noise ratio about 7 dB. Sufficient statistics from large data accumulation is necessary to reveal the observed effects of a few percent changes in the streaked diffraction signal. For example, to achieve a standard error on the 1% level, the number of pump-probe cycles required for averaging will be 400, translating into an acquisition time of 10 minutes. Note that in streaking mode, the fluctuations in electron charge and energy spectra can be averaged out without affecting the temporal resolution. This technique may also provide useful information on irreversible phenomena such as electronically driven phase transition of silicon41 in a single-shot fashion provided that a sufficiently sensitive detection system is available.
Upgrading our setup with a signal intensifier such as a micro-channel plate based detector or using a higher collection efficiency device, such as a fibre-optically coupled charged-coupled device camera could potentially enable orders of magnitudes increase in the signal-to-noise ratio. These enhancements are now within present technical capabilities so that laser-plasma accelerators could soon provide a path for sub-100-fs or even sub-10-fs ultrafast electron diffraction42.
Methods
Laser system
Laser pulses generated at 500 Hz repetition-rate with a centre wavelength of 0.8 μm and a full-width-at-half-maximum pulse duration of 35 fs, produced by the Relativistic Lambda-Cubed (λ3) laser system, were split into two optical beams by a pellicle beam splitter. One of them, containing the majority of the laser-pulse energy, was focussed onto argon gas flow by an f/2 off-axis parabola for the generation of the electron probe bunches. The second beam was frequency-doubled in a β-barium borate (BBO) crystal and focussed by a lens of focal length 10 cm for pumping the sample. A half-wave plate was installed before the BBO crystal to allow for the attenuation of the frequency-doubled light. A 2 mm BG40 bandpass filter and a low-dispersion 400 nm dielectric mirror were used to minimise the remaining energy at the fundamental wavelength. Calculating the dispersion for the pulse broadening effects from the optical elements used in the beam path yields a pulse duration of 150 fs. During the time calibration with the tungsten needle, the BBO crystal and BG40 filter were removed, and the dielectric mirror was replaced with one designed for near-infrared wavelengths to allow irradiation of the needle target at 800 nm. The optical pump beam size at the specimen plane was varied by translating the focussing lens along its optical axis. The relative temporal delay between the electron probe and optical pump was adjusted by an optical delay stage installed in the pump beam path.
Electron generation and diagnostics
Electrons were generated through the intense laser pulse interacting with a continuously flowing argon gas jet. The focussed laser pulse ionises the gas and excites plasma waves, which lead to emission of electron bunches via a process known as laser wakefield acceleration (see ref. 27 for the details of the acceleration mechanism). During normal operation, the vacuum chamber pressure remains below 10−3 mbar. After passing through an aperture, the electrons are nearly collimated by a solenoidal magnetic lens. Electrons were measured at 35 cm downstream on a high resolution scintillating screen (J6677 FOS by Hamamatsu), which was imaged using a lens coupled 14-bit electron-multiplying charged-coupled device camera (EMCCD, Andor Luca-R). The data in Fig. 4(c,f) was obtained with a conventional DC electron gun. Electrons were generated on a gold photocathode by a frequency tripled 266 nm Ti:sapphire laser, leading to a charge of approximately 2000 electrons per bunch at 1-kHz. Electrons were then accelerated to 45 keV by a DC field and collimated with a solenoidal lens. The Si sample was placed 40 mm after the photocathode, and the electron bunch duration was estimated to be 300 fs. Time-resolved data was taken in stroboscopic mode by recording a diffraction pattern for every pump-probe delay.
Sample fabrication
The Si nano-membrane samples are prepared from a silicon on insulator wafer43,44, which is composed of a 78 nm Si template layer, separated from a bulk Si handle wafer by a 400 nm buried oxide layer (BOX) and capped with a 150 nm thermal oxide to protect the template layer. An array of squares (350 μm × 350 μm each) are etched through the handle wafer with deep reactive ion etching (DRIE) using C4F8 and SF6, which etches through to the buried oxide etch stop. The capping oxide, and the buried oxide layer in the etched regions, are then selectively removed with hydrofluoric acid. This forms an array of Si nano-membranes supported only around their perimeter by the original silicon on insulator wafer. The entire structure is then thinned to 30 nm with CF4 reactive ion etching. It is clear from the optical micrograph in Fig. 1 that some rippling exists around the perimeter of the membranes, likely a consequence of strain relaxation in the membrane after the supporting BOX is removed. Nonetheless, large areas towards the centre remain relatively flat. A nano-membrane yield of approximately 50% results from both sample removal from the DRIE support and subsequent oxide stripping in hydrofluoric acid.
Data acquisition and analysis
Each streaked diffraction image was taken using about 300 electron pulses (0.6 s exposure time). Every pump “on” state exposure (I1) was immediately followed by a pump “off” shot (I0). Alternating between the signal and reference shots alleviates long-term stability issues such as heat accumulation and signal decrease of the electron charge due to drifting laser/gas profile conditions over the course of measurement. The data acquisition was automated to record about 1000 cycles, over a period of about 30 minutes. The signal ratio between the (220)-order and zero-order, i.e., the diffraction efficiency in every unpumped shot, was monitored to ensure that the induced effects in the sample were reversible within the sampling interval. The uncertainties in the relative signal R = I1/I0 were determined from the measurement using the standard error propagation  , which is shown for the 95% confidence interval in Fig. 4 and used as weights for the least-squares fitting.
, which is shown for the 95% confidence interval in Fig. 4 and used as weights for the least-squares fitting.
Additional Information
How to cite this article: He, Z.-H. et al. Capturing Structural Dynamics in Crystalline Silicon Using Chirped Electrons from a Laser Wakefield Accelerator. Sci. Rep. 6, 36224; doi: 10.1038/srep36224 (2016).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Schoenlein, R. et al. Generation of femtosecond pulses of synchrotron radiation. Science 287, 2237 (2000).
Khan, S., Holldack, K., Kachel, T., Mitzner, R. & Quast, T. Femtosecond undulator radiation from sliced electron bunches. Phys. Rev. Lett. 97, 074801 (2006).
McNeil, B. W. & Thompson, N. R. X-ray free-electron lasers. Nat. Photon. 4, 814 (2010).
Zewail, A. H. 4d ultrafast electron diffraction, crystallography, and microscopy. Annu. Rev. Phys. Chem. 57, 65 (2006).
Sciaini, G. & Miller, R. D. Femtosecond electron diffraction: Heralding the era of atomically resolved dynamics. Rep. Prog. Phys. 74, 096101 (2011).
Waldecker, L., Bertoni, R. & Ernstorfer, R. Compact femtosecond electron diffractometer with 100 keV electron bunches approaching the single-electron pulse duration limit. J. Appl. Phys. 117, 044903 (2015).
Baum, P. On the physics of ultrashort single-electron pulses for time-resolved microscopy and diffraction. Chem. Phys. 423, 55 (2013).
Baum, P. Towards ultimate temporal and spatial resolutions with ultrafast single-electron diffraction. J. Phys. B 47, 124005 (2014).
Gliserin, A., Walbran, M., Krausz, F. & Baum, P. Sub-phonon-period compression of electron pulses for atomic diffraction. Nat. Commun. 6, 8723 (2015).
van Oudheusden, T. et al. Compression of subrelativistic space-charge-dominated electron bunches for single-shot femtosecond electron diffraction. Phys. Rev. Lett. 105, 264801 (2010).
Chatelain, R. P., Morrison, V. R., Godbout, C. & Siwick, B. J. Ultrafast electron diffraction with radio-frequency compressed electron pulses. Appl. Phys. Lett. 101, 081901 (2012).
Gao, M. et al. Full characterization of rf compressed femtosecond electron pulses using ponderomotive scattering. Opt. Express 20, 12048 (2012).
Hastings, J. B. et al. Ultrafast time-resolved electron diffraction with megavolt electron beams. Appl. Phys. Lett. 89, 184109 (2006).
Musumeci, P., Moody, J. T., Scoby, C. M., Gutierrez, M. S. & Westfall, M. Laser-induced melting of a single crystal gold sample by time-resolved ultrafast relativistic electron diffraction. Appl. Phys. Lett. 97, 063502 (2010).
Muro’oka, Y. et al. Transmission-electron diffraction by MeV electron pulses. Appl. Phys. Lett. 98, 251903 (2011).
Murnane, M. M., Kapteyn, H. C., Rosen, M. D. & Falcone, R. W. Ultrafast x-ray pulses from laser-produced plasmas. Science 251, 531 (1991).
Rischel, C. et al. Femtosecond time-resolved x-ray diffraction from laser-heated organic films. Nature 390, 490 (1997).
Esarey, E., Schroeder, C. B. & Leemans, W. P. Physics of laser-driven plasma-based electron accelerators. Rev. Mod. Phys. 81, 1229 (2009).
Malka, V. Laser plasma accelerators. Phys. Plasmas 19, 055501 (2012).
Corde, S. et al. Femtosecond x rays from laser-plasma accelerators. Rev. Mod. Phys. 85, 1 (2013).
Lundh, O. et al. Few femtosecond, few kiloampere electron bunch produced by a laser-plasma accelerator. Nat. Phys. 7, 219 (2011).
Schumaker, W. et al. Ultrafast electron radiography of magnetic fields in high-intensity laser-solid interactions. Phys. Rev. Lett. 110, 015003 (2013).
Tokita, S., Inoue, S., Masuno, S., Hashida, M. & Sakabe, S. Single-shot ultrafast electron diffraction with a laser-accelerated sub-mev electron pulse. Appl. Phys. Lett. 95, 111911 (2009).
Tokita, S. et al. Single-shot femtosecond electron diffraction with laser-accelerated electrons: Experimental demonstration of electron pulse compression. Phys. Rev. Lett. 105, 215004 (2010).
Marceau, V., Varin, C., Brabec, T. & Piché, M. Femtosecond 240-keV electron pulses from direct laser acceleration in a low-density gas. Phys. Rev. Lett. 111, 224801 (2013).
Marceau, V., Hogan-Lamarre, P., Brabec, T., Piché, M. & Varin, C. Tunable high-repetition-rate femtosecond few-hundred keV electron source. J. Phys. B 48, 045601 (2015).
He, Z.-H. et al. High repetition-rate wakefield electron source generated by few-millijoule, 30 fs laser pulses on a density downramp. New J. Phys. 15, 053016 (2013).
Beaurepaire, B. et al. Effect of the laser wave front in a laser-plasma accelerator. Phys. Rev. X 5, 031012 (2015).
He, Z.-H. et al. Electron diffraction using ultrafast electron bunches from a laser-wakefield accelerator at kHz repetition rate. Appl. Phys. Lett. 102, 064104 (2013).
He, Z.-H. et al. Coherent control of plasma dynamics. Nat. Commun. 6, 7156 (2015).
Mourou, G. & Williamson, S. Picosecond electron diffraction. Appl. Phys. Lett. 41, 44 (1982).
Li, R. et al. Note: Single-shot continuously time-resolved MeV ultrafast electron diffraction. Rev. Sci. Instrum. 81, 036110 (2010).
Musumeci, P. et al. Capturing ultrafast structural evolutions with a single pulse of mev electrons: Radio frequency streak camera based electron diffraction. J. Appl. Phys. 108, 114513 (2010).
Eichberger, M. et al. Femtosecond streaking of electron diffraction patterns to study structural dynamics in crystalline matter. Appl. Phys. Lett. 102, 121106 (2013).
Harb, M. et al. Excitation of longitudinal and transverse coherent acoustic phonons in nanometer free-standing films of (001) Si. Phys. Rev. B 79, 094301 (2009).
Harb, M. et al. Carrier relaxation and lattice heating dynamics in silicon revealed by femtosecond electron diffraction. J. Phys. Chem. B 110, 25308 (2006).
Shank, C. V., Yen, R. & Hirlimann, C. Time-resolved reflectivity measurements of femtosecond-optical-pulse-induced phase transitions in silicon. Phys. Rev. Lett. 50, 454 (1983).
Yoffa, E. J. Screening of hot-carrier relaxation in highly photoexcited semiconductors. Phys. Rev. B 23, 1909 (1981).
Beaurepaire, B., Lifschitz, A. & Faure, J. Electron acceleration in sub-relativistic wakefields driven by few-cycle laser pulses. New J. Phys. 16, 023023 (2014).
Goers, A. J. et al. Multi-MeV electron acceleration by subterawatt laser pulses. Phys. Rev. Lett. 115, 194802 (2015).
Harb, M. et al. Electronically driven structure changes of Si captured by femtosecond electron diffraction. Phys. Rev. Lett. 100, 155504 (2008).
Faure, J. et al. Concept of a laser-plasma-based electron source for sub-10-fs electron diffraction. Phys. Rev. Accel. Beams 19, 021302 (2016).
Scott, S. A. & Lagally, M. G. Elastically strain-sharing nanomembranes: flexible and transferable strained silicon and silicon-germanium alloys. J. Phys. D: Appl. Phys. 40, R75 (2007).
Cavallo, F. & Lagally, M. G. Semiconductors turn soft: inorganic nanomembranes. Soft Matter 6, 439 (2010).
Acknowledgements
This work was supported by the US Air Force Office of Scientific Research under award number FA9550-12-1-0310, the US National Science Foundation under contract 1535628 and the US Department of Energy under contract DE-NA0002372. Fabrication and characterisation of Si nano-membrane samples (S.A.S. and M.G.L.) was supported by the US Department of Energy Grant #DE-FG0203ER46028. J.F. acknowledges the support of the European Research Council, contract No. 306708, ERC Starting Grant FEMTOELEC).
Author information
Authors and Affiliations
Contributions
Z.-H.H. directed the laser wakefield experiment with the participation of B.B., J.A.N., J.F. and analysed the results. G.G. and J.F. directed the electron gun experiment and analysed the results. S.A.S., J.R.S.P. and M.G.L. prepared the Si membranes. Z.-H.H. and J.F. wrote the manuscript. J.F., A.G.R.T., K.K. and J.A.N. provided overall supervision for the project. All authors discussed the results and contributed to the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
He, ZH., Beaurepaire, B., Nees, J. et al. Capturing Structural Dynamics in Crystalline Silicon Using Chirped Electrons from a Laser Wakefield Accelerator. Sci Rep 6, 36224 (2016). https://doi.org/10.1038/srep36224
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep36224
This article is cited by
-
Laser-driven low energy electron beams for single-shot ultra-fast probing of meso-scale materials and warm dense matter
Scientific Reports (2023)
-
Dual-energy electron beams from a compact laser-driven accelerator
Nature Photonics (2019)
-
Relativistic electron beams driven by kHz single-cycle light pulses
Nature Photonics (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.