Introduction

The study of ion transport in fluids is an important topic with a wide range of applications. Some classic examples are batteries, fuel cells, electroplating, and protection of metal structures against corrosion1. In addition to the traditional battery, the flow battery or rechargeable fuel cell2,3 represents an important new technology involving the transport of ions. Ion exchange membranes have a wide range of applications4, and the underlying theory has been a matter of concern for several decades5. Other examples of complex electro-chemical systems are the transport of charged particles in ion channels6,7,8, in protein channels9, and during the primordial conversion of light to metabolic energy10. Often upscaling is necessary for a complete analysis of the transport of electrolytes in charged pores11,12.

Much of ion transport occurs at the nano-scale13, and most of the studies use the Nernst-Planck equation14,15,16 to describe this type of phenomena. However, there are molecular dynamic simulations indicating that the Nernst-Planck equation does not always provide a complete description17, and there are experimental studies that lead to the same conclusion18. The need to analyze the limits of the Nernst-Planck contribution to diffusion has been emphasized19 in an exploration of the transport of divalent ions in ionic channels.

The authors of this paper have not found a derivation of the Nernst-Planck equation that does not make use of the ideal gas assumption. To be precise we note that ideal gas behavior for mixtures is based on Dalton’s laws (see page 114 in ref. 20) that we list as

Some care must be taken with the interpretation of Eq. 2 since it applies to all Stokesian fluids and is therefore not limited to ideal gas mixtures (see Appendix B in ref. 21). Caution must also be used with the interpretation of Eq. 3 which is applicable to all ideal fluid mixtures. For example, Eq. 3 should provide reliable results for a liquid mixture of hexane and heptane, but it should not for a mixture of ethanol and water.

Here it is important to emphasize that Eq. 1 can only describe a fluid composed of non-interacting particles. To provide a reliable framework in which a fluid is considered to be composed of interacting particles ̶ as in the case of a liquid ̶ it is necessary to understand the process of Nernst-Planck diffusion in a fluid different from an ideal gas. This is the problem under consideration in this paper.

In this work we analyze the ion transport process from a fundamental point of view using an axiomatic mechanical perspective. Our analysis is for ideal fluid mixtures, and from the analysis we find that the classic Nernst-Planck relation is only valid for ideal gas mixtures. For ideal liquid mixtures we find an alternative expression in which the form is similar to that for ideal gas mixtures, but significant other terms appear in the final result.

In the following section we present a detailed analysis based on axiomatic statements for the mechanics of multi-component systems. Our objective is a search for clarity and rigor in terms of a diffusion equation that is applicable to both gas and liquid mixtures, i.e., applicable to fluid mixtures. We first derive a general equation for the species velocity, and from this we extract a general equation for the species diffusion velocity. This equation is the origin of Fick’s law of diffusion; however, the derivation of Fick’s law from the governing equation for the species diffusion velocity is complex. We begin our study of the general equation for the species diffusion velocity with a series of plausible restrictions that lead to a special form of the governing equation for the diffusion velocity. This provides a transport equation for the diffusion of charged molecules in fluids, and this general form can be used to clearly establish that the classic Nernst-Planck equation is only valid for ideal gas mixtures.

Analysis

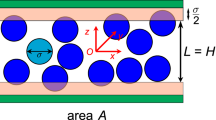
The analysis in this study is presented in terms of axiomatic statements concerning the species A body illustrated in Fig. 1. There we have used VA(t) to identify the volume occupied by the species A body, and we have illustrated only the presence of one other species, species B; however, one should image the presence of many other species. We begin with a review of the axioms for mass and mechanics of multi-component systems, and then move on to explore the dominant terms in the species momentum equation. If one accepts the simplification that the electric field represents a specified force, the motion of both charged and uncharged species can be treated in terms of the axioms for mass and momentum that are given in the following paragraphs. It is crucial to understand that the following development is applicable to both gases and liquids.

Figure 1
figure 1

Species A Body.

Full size image

Mass

We begin our study with the two axioms for mass given by

The volume of the species A body is represented by VA(t) and the speed of displacement of the surface of this volume is vA·n. Axiom I A can be used to derive the species A continuity equation by using the transport theorem and the divergence theorem (see Sec. 1.3.2 in ref. 22). This leads to

The total continuity equation is obtained by summing Eq. 6 over all N species and imposing Eq. 5 in order to obtain (see page 83 in ref. 23)

Here the total density, ρ, and the total mass flux, ρv, are defined by

The mass fraction of species A is defined according to

and use of this definition with Eq. 8 provides a constraint for the mass fractions and a representation for the mass average velocity. These two results take the form

The objective of this study is the development of an expression for the diffusive flux of species A. This requires that we decompose the species velocity according to

in which uA is the mass diffusion velocity. This decomposition allows us to express Eq. 6 in terms of convective and diffusive fluxes according to (see Eq. 19.1–7 in ref. 23)

Here we note that the mass diffusive flux is defined by

and this flux is constrained by

Given these forms of the species continuity equation and the total continuity equation, we are ready to move on to the analysis of the mechanics of multi-component fluids.

Mechanics

The first of the four axioms associated with the species A body is the linear momentum principle given by (see page 85 in ref. 24)

Here the species stress vector, tA(n), represents the force that the surroundings (into which n is directed) exert on species A within the species A body. We have used PAB to represent the diffusive force exerted by species B on species A and it is understood that

In the last term in Eq. 15 we have indicated the possibility that species A entering or leaving the species A body owing to chemical reaction may have a velocity different than the continuum velocity vA.

The second axiom is the angular momentum principle that takes the form

Here r represents the position vector relative to a fixed point in an inertial frame. Truesdell (see page 85 in ref. 24) presents a more general version of Axiom II B in which a growth of rotational momentum is included, and Aris (see Sec. 5.13 in ref. 25) considers an analogous effect for polar fluids.

The third axiom requires that there be no net diffusive force in the total momentum equation (see page 133 in ref. 26) and we express this idea as

In terms of chemical reactions, Hirschfelder et al. (see page 497 in ref. 27) point out that “even in a collision which produces a chemical reaction, mass, momentum and energy are conserved”. The continuum version of this idea for linear momentum gives rise to the fourth axiom that we express as

Returning to Eq. 15 we note that Axiom I B can be used to develop Cauchy’s lemma given by (see Section 203 in ref. 28)

in which tA(−n) represents the force that species A exerts on the surroundings. Cauchy’s fundamental theorem for the species stress vector is given by (see Lecture 5 in ref. 24).

and one can use this result in Eq. 15 to obtain the following

Species A Momentum Equation:

At this point we can use the continuity equation given by Eq. 6 to obtain

and this allows us to express Eq. 22 in the form

Both Eq. 22 and Eq. 24 can be found in the literature; however, locating them requires some effort because of the lack of a uniform nomenclature (see Sec. 1.2 in ref. 21). Chapman and Cowling (see page 135 in ref. 29) obtained Eq. 24 for dilute gases with rA = 0 by means of a generalized equation of change. In addition, this result was presented by Truesdell and Toupin (see Eq. 215.2 in ref. 28) and by Truesdell (see Eq. 22 in ref. 30). Bearman and Kirkwood (see Eq. 4.20 in ref. 31) presented Eq. 22 for the case of rA = 0 as did Curtiss and Bird (see Eq. A2 in ref. 32). Datta and Vilekar (see Eq. 2 in ref. 33) have derived Eq. 22 beginning with Eq. 15, and Jou et al. (see Eq. 1.21 in ref. 34) present Eq. 22 with the last two terms identified as “…contributions due to the interaction forces and the exchange of momentum between various components…” Most recently the developments leading to Eqs 22 and 24 have been summarized by Whitaker (see ref. 35).

The analysis of Axiom II B is rather long; however, after some algebra one finds that Eq. 17 leads to the symmetry of the species stress tensor indicated by (see Lecture 5 in ref. 24)

This is identical in form to Cauchy’s second law of motion (see page 187 in ref. 36). At this point it seems clear that there is general agreement concerning the form of the species linear momentum equation that represents the governing equation for the species velocity, vA. In the study of diffusion processes, it is the diffusion velocity, uA, that is important, and in the following paragraphs we develop the governing equation for this velocity.

Diffusion Velocity

The total linear momentum equation is obtained by summing Eq. 22 over all species and imposing the axioms given by Eqs 18 and 19. This leads to

in which the total stress tensor and the total body force are defined by

At this point we recall that a Stokesian fluid (see Sec. 59 of ref. 37, see Sec. 5.21 of ref. 25, see Secs. 3.3 and 3.4 of ref. 38, see Sec. 2.3.2 of ref. 22) can be described by:

Here τ is the viscous stress tensor, and p is the local thermodynamic pressure given by

in which e is the internal energy per unit mass. To relate this expression for the pressure to that given by Slattery (see page 444 of ref. 22) and to that given by Callen (see Eq. 2.4 of ref. 39), one makes use of the following

Here m represents the mass of the closed system preferred by Callen39. Use of Eq. 28 with Eq. 26 allows us to express the total momentum equation in the form

Returning to the species momentum equation given by Eq. 22, we propose that the species stress tensor can be represented by

Here pA is the partial pressure defined by (see Chapter 10 of ref. 40)

in which eA is the internal energy of species A per unit mass of species A. The classic relation between the partial pressures and the total pressure is given by

and this requires that

The proof of this result is rather long and is given by Whitaker (see Appendix B of ref. 21). We can use Eq. 27 through Eq. 34 to conclude that

It is important to recognize that the application of Eqs 29 and 33 requires an assumption of local thermodynamic equilibrium (see Sec. 3.4 of ref. 38), and this should be satisfactory for many, but not all, mass transfer processes. The use of Eq. 32 in Eq. 22 leads to the following form of the species A momentum equation

Here one should note that the diffusive force is constrained by Eq. 16.

At this point it will be convenient to use Eq. 7 with Eq. 26 to obtain the following form of the total momentum equation

The analogous form of the species momentum equation is given by Eq. 24 and repeated here as

At this point we wish to use Eqs 38 and 39 to derive the governing equation for the mass diffusion velocity, uA. We begin by multiplying Eq. 38 by the mass fraction ωA leading to

and we subtract this result from Eq. 39 to obtain the desired governing differential equation for the mass diffusion velocity, uA, given by

This governing equation for uA is the origin of Fick’s law (see Eq. 1 of ref. 41; see page 45 of ref. 42); however, some simplifications are required in order to achieve that classic result. To be clear about this point, we note that Fick’s law for a binary system is given by (see Table 17.8-2 of ref. 23)

and the path between Eq. 41 and Eq. 42 is rather long (see Eq. 110 of ref. 21).

We now make use of Eqs 28 and 32 with Eq. 41 to obtain the following form of the governing equation for the species A mass diffusion velocity

Plausible restrictions associated with this governing equation for uA are given by (see Sec. 1.2 in ref. 21) and are listed here as

An effort to justify these restrictions is given by Whitaker (see Secs. 2.6 and 2.7 in ref. 43); however, a rigorous analysis leading to constraints is still unavailable. Equation 44 indicates that the governing equation for uA is quasi-steady; Eq. 45 indicates that diffusive inertial effects are negligible, Eq. 46 indicates that the influence of mass average rotational flow is negligible, Eq. 47 indicates that viscous effects are negligible, Eq. 48 indicates that diffusive stresses are negligible, and Eq. 49 indicates that the effects of homogeneous chemical reactions are negligible. When the restrictions given by Eqs 44 through 49, are imposed, the governing equation for the mass diffusion velocity takes the form

Curtiss & Bird (see Eq. 7.6 in ref. 44) represent the left hand side of Eq. 50 by cRTdA and refer to it as the generalized driving force for diffusion. Truesdell (see Eq. 7 in ref. 30) represents the left hand side of Eq. 50 by pdA and cites27 as the source. To illustrate the connection with27, we need Eq. 3 repeated here as

Use of this representation for the partial pressure indicates that our analysis is restricted to ideal fluid mixtures and it allows us to express Eq. 50 in the form

The left hand side of this result is identical to Enskog’s perturbation solution45 (see Eq. 7.3–27 in ref. 27). This indicates that the simplifications represented by Eqs 44 through 49 are consistent with the perturbation analysis45. It is important to keep in mind that Eq. 50 represents a special form of the governing equation for the diffusion velocity, uA, subject to the restrictions indicated by Eqs 44 through 49. In addition, this equation for the diffusion velocity is restricted by the thermodynamic results indicated by Eqs 29 and 33. Finally, we remind the reader that Eq. 50 is a continuum result that is not restricted to either gases or liquids but is restricted to Stokesian fluid mixtures.

We begin our analysis of Eq. 52 by neglecting the pressure diffusion term. This represents a satisfactory simplification for many diffusion processes; however, it is not acceptable for centrifugation processes (see page 776 in ref. 23; see page 452 in ref. 42). Given this simplification, Eq. 52 takes the form

and we are ready to analyze the term on the right hand side.

Diffusive Force

From dilute gas kinetic theory we know that PAB|gas is given by

This result can be obtained by comparing Eq. 52 of this work with Eqs 7.3–27 and 7.4–48 of ref. 27 and neglecting the effect of thermal diffusion. At this point we need a representation for PAB|liq, and one possibility is to use Eq. 54 as a model. This leads to

where it is understood that all the terms on the right side are associated with a liquid mixture. It should be clear that Eq. 55 represents an empirical expression for the diffusive force, PAB|liq, and that DAB represents an empirical coefficient to be determined by experiment. We can generalize Eqs 54 and 55 to the single form

in which the diffusivity is given by

Use of Eq. 56 in Eq. 53 leads to

In Appendix A we show that for dilute solutions we obtain the result given by

Here JA represents the mixed-mode diffusive flux (see page 537, Eq. H in ref. 23, see Sec. 4, Eq. 90 in ref. 21) defined according to

and is a mixture diffusion coefficient given by

We refer to JA as the mixed-mode diffusive flux since it is made up of the molar concentration, cA, and the mass diffusion velocity, uA.

Use of Eq. 60 in Eq. 59 allows us to express the mixed-mode diffusive flux according to

At this point we make use of the analysis given in Appendix B where we demonstrate the well-known result given by (see page 776 in ref. 23)

Here zAF represents the charge per mole of species A in which zA is the valence (i.e., −2 for and +1 for H3O+) and F is the conversion factor known as Faraday’s constant. It is important to note that Eq. 64 is subject to the approximation of electro-neutrality (see page 454 in ref. 42; see ref. 46) and this simplification will not be valid near charged surfaces11. Use of Eq. 64 in Eq. 63 leads to the following result

At this point we impose the dilute solution condition given by

so that Eq. 65 takes the form

In order to represent the second term on the right hand side of Eq. 67 in terms of what is usually called Nernst-Planck diffusion, we introduce the product RT and arrange that term to obtain the following result

For ideal gas mixtures we have cRT/p = 1 and the diffusivity takes the form as indicated by Eq. 57, Eq. A10 and Eq. A13. Under these circumstances Eq. 68 simplifies to the classic Nernst-Planck equation (see page 149 in ref. 47, see Eq. 3 in ref. 11, see Eq. 11. in ref. 42, see page 1844 in ref. 48) given by

For liquid mixtures we have cRT/p = cliqRT/pliq and the diffusivity takes the form as indicated by Eq. 58, Eq. A10, and Eq. A16. Under these circumstances Eq. 68 takes the form

At this point it is important to realize that cliqRT/pliq ≈ 1200 and there is no simplification of Eq. 68 to the form given by Eq. 69 for liquid phase diffusion. The development based on Eqs 54 and 55 is not the only route to Eqs 69 and 70, and another approach making use of the relation pga = cgasRT is given in Appendix C.

The analysis presented here indicates that the classic result for dilute solution diffusion of ions in an electric field is only valid for ideal gas mixtures. When confronting this situation one must keep in mind that the results given in Appendix A for the third term in Eq. 53 would appear to be universally accepted (see page 47 in ref. 49, see page 19 in ref. 47, see page 448 in ref. 42). In addition, the result given in Appendix B for the second term in Eq. 53 would also appear to be universally accepted (see page 279 in ref. 49, see page 454 in ref. 42, see page 776 in ref. 23).

Conclusions

In this paper we have derived an ion transport equation for ideal fluid mixtures, and we have shown that the classic Nernst-Planck equation applies only to ideal gas mixtures. For ideal liquid mixtures, the laws of mechanics, the laws of electrostatics, and the thermodynamic representation for the partial pressure all lead to a new result. Non-ideal gases and liquids can be analyzed using the approach presented in this paper; however, that subject has not been explored in this work50,51.

Nomenclature

bA = body force per unit mass exerted on species A, N/kg

b = , body force per unit mass exerted on the mixture, N/kg

cA = molar concentration of species A, mol/m3

c = total molar concentration, mol/m3

= , ideal gas binary diffusion coefficient for species A and B, m2/s

= ideal gas mixture diffusivity for species A, m2/s

DAB = DBA, dilute solution liquid-phase binary diffusion coefficient for species A and B, m2/s

DA = dilute solution mixture diffusivity for species A, m2/s

E = electric field, V/m

F = Faraday’s constant, 9.652 × 104 coulombs/mol

g = gravitational body force per unit mass, N/kg

l = unit tensor

JA = cAuA, mixed-mode diffusive flux of species A, mol/ m2s

n = unit normal vector

N = total number of molecular species

PAB = diffusive force per unit volume exerted by species B on species A, N/m3

pA = partial pressure of species A, N/m2

p = , total pressure, N/m2

rA = net mass rate of production of species A owing to homogeneous reactions, kg/m3s

R = gas constant, cal/mol K50

t = time, s

= stress tensor for species A, N/m2

= total stress tensor, N/m2

T = temperature, K

uA = vA − v, mass diffusion velocity, m/s

vA = velocity of species A, m/s

v = , mass average velocity, m/s

xA = cA/c, mole fraction of species A

zA = valence (±) for ionic species A

Greek Letters

ρA = mass density of species A, kg/m3

ρ = total mass density, kg/m3

τ = viscous stress tensor, N/m2

τA = viscous stress tensor for species A, N/m2

ωA = ρA/ρ, mass fraction of species A

Ψ = electric potential function, V

Additional Information

How to cite this article: del Río, J. A. and Whitaker, S. Diffusion of Charged Species in Liquids. Sci. Rep. 6, 35211; doi: 10.1038/srep35211 (2016).