Introduction

Quantum coherence, being at the heart of quantum mechanics, plays a key role in quantum information processing such as quantum algorithms1 and quantum key distribution2. Inspired by the recently proposed resource theory of quantum coherence3,4, researches are focused on the quantification5,6 and evolution7,8 of quantum coherence, as well as its operational meaning5,9 and role in quantum information tasks10,11,12. When multipartite systems are considered, coherence is closely related to the well-established quantum information resources, such as entanglement13 and discord-type quantum correlations14. It is shown that the coherence of an open system is frozen under the identical dynamical condition where discord-type quantum correlation is shown to freeze15. Further, discord-type quantum correlation can be interpreted as the minimum coherence of a multipartite system on tensor-product basis16. An operational connection between local coherence and non-local quantum resources (including entanglement17 and discord18) is presented. It is shown that entanglement or discord between a coherent system and an incoherent ancilla can be built by using incoherent operations, and the generated entanglement or discord is bounded from above by the initial coherence. The converse procedure is of equal importance: to extract coherence locally from a spatially separated but quantum correlated bipartite state. The extraction of coherence with the assistance of a remote party has been studied in the asymptotical limit19. In this paper, we ask how we extract coherence locally from a single copy of a bipartite state.

The quantum steering has long been noted as a distinct nonlocal quantum effect20 and has attracted recent research interest both theoretically and experimentally21,22,23,24,25,26,27,28,29,30,31. It demonstrates that Alice can remotely change Bob’s state by her local selective measurement if they are correlated, and is hence a natural candidate to accomplish the task of remote coherence extraction.

In this paper, we present the study of coherence extraction induced by quantum steering and the involved quantum correlation. Precisely, we introduce the quantity of steering-induced coherence (SIC) for bipartite quantum states. Here Bob is initially in an incoherent state but quantum correlated to Alice. Alice’s local projective measurement can thus steer Bob to a new state which might be coherent. The SIC is then defined as the maximal average coherent of Bob’s steered states that can be created by Alice’s selective projective measurement. When there is no obvious incoherent basis for Bob, (for example, Bob’s system is a polarized photon), the definition can be generalized to arbitrary bipartite system where Bob’s incoherent basis is chosen as the eigenbasis of his reduced state. In this case, the SIC can be considered as a basis-free measure of Bob’s coherence. The main result of this paper is building an operational connection between the SIC and the shared quantum correlation between Alice and Bob. We prove that the SIC can not surpass the initially shared B-side quantum correlation, which is a known quantum correlation measure named as measurement-induced disturbance (MID) 32. States whose relative entropy SIC can reach its upper bound are identified as maximally correlated states. For two-qubit states, while the trace-norm SIC can always reach the corresponding , we find an example of two-qubit state whose is strictly less than . This indicates that the condition for to reach the upper bound strongly depends on the measure of coherence. We further generalize the results to a tripartite scenario, where Alice can induce entanglement between Bob and Charlie in a controlled way. Since coherence of a single party is generally robust than quantum correlations involving two parties, our work provides a way to “store” quantum correlation as coherence. Besides, the coherent state induced by steering can be widely used for quantum information processing. Our results establish the intrinsic connection between coherence and quantum correlation by steering.

Results

Coherence and measurement-induced disturbance

A state is said to be incoherent on the reference basis , if it can be written as3

Let be the set of incoherent state on basis Ξ. The incoherent completely positive trace-preserving (ICPTP) channel is defined as

where the Kraus operators Kn satisfy . According to ref. 3, a proper coherence measure of a quantum state ρ on a fixed reference basis Ξ should satisfy the following three conditions. (C1) C(ρ, Ξ) = 0 iff . (C2) Monotonicity under selective measurements on average: satisfying and , where , occurring with probability , is the state corresponding to outcome n. (C3) Convexity: .

A candidate of coherence measure is the minimum distance between ρ and the set of incoherent states

where is a distance measure on quantum states and satisfies the following five conditions. (D1) D(ρ, σ) = 0 iff ρ = σ. (D2) Monotonicity under selective measurements on average: . (D3) Convexity: . (D4) , , where U is a unitary operation, and denotes the projective measurement on basis Ξ: . (D5) . Conditions (D1-D3) make sure that (C1-C3) is satisfied by the coherence measure defined in Eq. (3). When (D4) is satisfied, the coherence of ρ on the reference basis Ξ can be written as

As proved in ref. 3, the relative entropy and the l1 matrix norm satisfies all the conditions (D1-D4), which makes the corresponding coherence measures and satisfy the conditions (C1-C3). As discovered recently33, the trace-norm distance does not satisfy (D2).

Introduced in ref. 32, MID characterizes the quantumness of correlations. MID of a bipartite system ρ is defined as the minimum disturbance caused by local projective measurements that do not change the reduced states and

where the infimum is taken over projective measurements which satisfy and , and is a distance on quantum states, which satisfies conditions (D1-D5) and further (D6) . It can be checked that (D6) can be satisfied by relative entropy but not satisfied by l1-norm. Comparing Eq. (5) with Eq. (4), we find MID is just the coherence of the bipartite state ρ on the local eigenbasis .

For later convenience, we introduce B-side MID as

goes to zero for B-side classical states, which can be written as , while is strictly positive for if . Notice that for one do not have a coherence interpretation.

Definition of steering-induced coherence

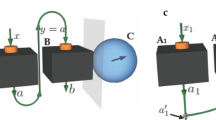
As shown in Fig. 1, Alice and Bob initially share a quantum correlated state ρ, and Bob’s reduced state ρB is incoherent on his own basis. Now Alice implements a local projective measurement on basis ΞA. When she obtains the result i (which happens with probability ), Bob is “steered” to a coherent state . We introduce the concept of SIC for characterizing Alice’s ability to create Bob’s coherence on average using her local selective measurement.

Figure 1: Scheme for creating Bob’s coherence by Alice’s local measurement and classical communication.
figure 1

When Alice implements local projective measurement on basis , she gets result i with probability and meanwhile steer Bob’s state to which can be coherent on Bob’s initial eigenstate . SIC is defined as the maximal average coherence of states that can be created by Alice’s local selective measurement.

Full size image

Definition (Steering-induced coherence, SIC)

For a bipartite quantum state ρ, Alice implements projective measurement on basis (). With probability , she obtains the result , which steers Bob’s state to . Let () be the eigenbasis of reduced states ρB. The steering-induced coherence is defined as the maximum average coherence of Bob’s steered states on the reference basis

where the maximization is taken over all of Alice’s projective measurement basis ΞA, and the infimum over is taken when ρB is degenerate and hence is not unique.

Since Bob’s initial state ρB is incoherent on its own basis , the SIC describes the maximum ability of Alice’s local selective measurement to create Bob’s coherence on average. We verify the following properties for .

(E1) , and iff ρ is a B-side classical state.

(E2) Non-increasing under Alice’s local completely-positive trace-preserving channel: .

(E3) Monotonicity under Bob’s local selective measurements on average: satisfying , where and .

(E4) Convexity: .

Proof. Condition (E1) can be proved using the method in ref. 31, where it is proved that vanishes iff ρ is a B-side classical state. (E2) is verified by noticing that the local channel can not increase the set of Bob’s steered states, and hence the optimal steered states may not be steered to after the action of channel . The conditions (E3) and (E4) are directly derived from conditions (C2) and (C3) for coherence.

Relation between SIC and MID

Intuitively, Alice’s ability to extract coherence on Bob’s side should depend on the quantum correlation between them. The following theorem gives a quantitative relation between the SIC and quantum correlation measured by B-side MID .

Theorem 1. When the distance measure in the definition of MID and coherence satisfies conditions (D1-D6), the SIC is bounded from above by the B-side MID, i.e.,

Proof. We start with the situation that ρB is non-degenerate and hence one do not need to take the infimum in Eqs (5) and (7). By definition, we have

where .

After Alice implements a selective measurement on basis ΞA, the average coherence of Bob’s state becomes

The second equality holds because (condition (D5)) and . Since selective measurement does not increase the state distance (condition (D2)), we have , and hence Eq. (8) holds.

The generalization to degenerate state is straightforward. We choose to reach the infimum of , which may not be the optimal eigen-basis for . Hence we have .

According to ref. 17, the coherence of a quantum system B can in turn be transferred to the entanglement between the system and an ancilla C by incoherent operations. The established entanglement, measured by the minimum distance between the state ρBC and a separable state as , is bounded from above by the initial coherence of B. Here is the set of separable states and the state distance D is required not to increase under trace-preserving channels , which is automatically satisfied when we combine conditions (D2) and (D3).

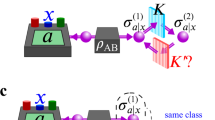
This leads to the three-party protocol as shown in Fig. 2, where Alice’s local selective measurement can create entanglement between Bob and Charlie. In this protocol, Bob and Charlie try to build entanglement between them from a product state , but are limited to use incoherent operations. Since ρB is incoherent on his eigenbasis , Bob and Charlie can build only classically correlated state without Alice’s help. Now Alice implement projective measurement and on the outcome i, the state shared between Bob and Charlie is steered to which can be entangled. The following corollary of theorem 1 gives the upper bound of the steering-induced entanglement.

Figure 2: Scheme for creating entanglement between Bob and Charlie by Alice’s local selective measurement.
figure 2

When Alice implements local projective measurement on basis , she gets result i with probability and meanwhile steer the state shared between Bob and Charlie to which can be entangled.

Full size image

Corollary 1 Alice, Bob and Charlie share a tripartite state ρ, which is prepared from the product state using an ICPTP channel on BC: . Here is the reference basis of coherence. Alice’s local selective measurement can establish entanglement between Bob and Charlie, and the established entanglement on average is bounded from above by the initial B-side MID between Alice and Bob

Proof. Before Alice implement the measurement, the state shared between Bob and Charlie is incoherent on basis and hence can be written as . Apparently, , so Bob and Charlie is classically correlated.

On the measurement outcome i, the entanglement between Bob and Charlie becomes which satisfies . Notice that and hence . Eq. (11) is arrived by noticing that from theorem 1.

Now we consider a general tripartite state ρ. If the reduced state is non-degenerate, one can follow the same steps and prove that

whenever ρBC is incoherent on basis . Here is the {BC}-side MID between Alice and the combination of Bob and Charlie. However, when ρBC is degenerate, the condition that the tripartite state ρ is prepared from by an ICPTP channel on BC is stringent. For example, the state where , with ρBC incoherent on basis , violates Eq. (12), since but the left-hand-side reaches unity for Alice’s measurement basis . It indicate that the state ρX can not be prepared from a product state in the form using only incoherent operations.

States to reach the upper bound

According to theorem 1, Bob’s maximal coherence that can be extracted by Alice’s local selective measurement is bounded from above by the initial quantum correlation between them. Since the relative entropy is the only distance measure found to date which satisfies all the conditions (D1-D6), we employ relative entropy as the distance in the definition of coherence and MID, and discuss the states which can reach the upper bound of theorem 1.

Theorem 2. The SIC can reach B-side MID

for maximally correlated states .

Proof. Any maximally correlated state can be written in a pure state decomposition form with and . Here has eigenbasis . In order to calculate the B-side MID, we consider Bob’s projective measurement , which takes the bipartite state to . Apparently, . By definition, we have

In order to extract the maximum average coherence on Bob’s side, Alice measures her quantum system on basis , where , and dA is the dimension of A. On the measurement result k, Bob’s state is steered to where , which happens with probability . Apparently, and hence . Meanwhile, we have . The coherence of steered state is then

for any outcome k. Therefore we arrive at Eq. (13).

Any pure bipartite state can be written in a Schmidt decomposition form , and hence belongs to the set of maximally correlated states. As introduced in ref. 17, a maximally correlated states ρmc is prepared from an product states using an incoherent unitary operator, and its entanglement E(ρmc) can reach the initial coherence of ρB. Further, for maximally correlated states, one can check the equality, . Therefore, ρmc can be used in a scenario where coherence is precious and entanglement is not as robust as single-party coherence. Precisely, consider the situation where Alice and Bob share a maximally correlated state but they are not use it in a hurry. To store the resource for latter use, she can transfer the entanglement between them into Bob’s coherence using her local selective measurement. Bob stores his coherent state as well as Alice’s measurement results. When required, Bob can perfectly retrieve the entanglement by preparing a maximally correlated state using only incoherent operations.

Two-qubit case, relation between l1-norm of SIC and trace-norm distance of B-side MID

One cannot define MID based on the l1-norm distance, since it does not satisfy (D6) in general. However, it can be checked that for single-qubit states ρB and σB, 34, where rρ and rσ are Bloch vectors of ρB and σB respectively. Hence the l1-norm of coherence for a single-qubit state ρB can be written as

Besides, Dt, which satisfies condition (D6), is proper to be used as a distance measure for MID. Therefore, when the Bob’s particle is a qubit, it is meaningful to study the relation between l1-norm of SIC and trace-norm distance of B-side MID. Now we consider a two-qubit state ρ, and employ in the definition of as in Eq. (7) and prove the following theorem.

Theorem 3. For a two-qubit state ρ, we have

Proof. The state of a two-qubit state can be written as , where the coefficient matrix can be written in the block form .

For non-degenerate case b ≠ 0, we choose the eigenbasis of ρB for the basis of density matrix and hence b = (0, 0, b3). Further, a proper basis of qubit A is chosen such that the matrix T is in a triangle form with . We calculated the explicit form of and and obtain

For degenerate case with b = 0, we can always chose proper local basis such that T is diagonal. Here we impose T11 ≥ T22 ≥ T33 without loss of generality. Direct calculations lead to

We check that, for the state , we have , but according to theorem 3, . It means that relative entropy of coherence and -norm of coherence are truly different measures of coherence.

Discussion

In this paper, we have introduced the notion of SIC which characterizes the power of Alice’s selective measurement to remotely create quantum coherence on Bob’s site. Quantitative connection has been built between SIC and the initially shared quantum correlation measured by -side MID. We show that SIC is always less than or equal to -side MID. Our results are also generalized to a tripartite scenario where Alice can build the entanglement between Bob and Charlie in a controlled way.

Next, we discuss a potential application of SIC in secrete sharing. Suppose Alice and Bob share a two-qubit state , whose SIC reaches unity. When Alice measures her state on different basis, Bob’s state is steered to, e.g., or with . The coherence of states in reach unity on basis and vise visa. Consequently, when we measure the states in the set on basis , the outcome is completely random. It is essential to quantum secret sharing using . In this sense, the SIC is potentially related to the ability for Alice to share secret with Bob.

Coherence and various quantum correlations, such as entanglement and discord-like correlations, are generally considered as resources in the framework of resource theories9,35. By coining the concept of SIC, we present an operational interpretation between measures of those two resources, SIC and MID, and open the avenue to study their (ir)reversibility. The applications of various coherence quantities like SIC in many-body systems, as in the case of entanglement36,37,38, can be expected.

Additional Information

How to cite this article: Hu, X. and Fan, H. Extracting quantum coherence via steering. Sci. Rep. 6, 34380; doi: 10.1038/srep34380 (2016).