Abstract
Here we consider using quantum annealing to solve Set Cover with Pairs (SCP), an NP-hard combinatorial optimization problem that plays an important role in networking, computational biology and biochemistry. We show an explicit construction of Ising Hamiltonians whose ground states encode the solution of SCP instances. We numerically simulate the time-dependent Schrödinger equation in order to test the performance of quantum annealing for random instances and compare with that of simulated annealing. We also discuss explicit embedding strategies for realizing our Hamiltonian construction on the D-wave type restricted Ising Hamiltonian based on Chimera graphs. Our embedding on the Chimera graph preserves the structure of the original SCP instance and in particular, the embedding for general complete bipartite graphs and logical disjunctions may be of broader use than that the specific problem we deal with.
Similar content being viewed by others
Introduction
Quantum annealing (QA) uses the principles of quantum mechanics for solving unconstrained optimization problems1,2,3,4. Since the initial proposal of QA, there has been much interest in the search for practical problems where it can be advantageous with respect to classical algorithms4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33, particularly simulated annealing (SA)34,35,36. Extensive theoretical, numerical and expeirmental efforts have been dedicated to studying the performance of quantum annealing on problems such as satisfiability37,38,39, exact cover3,39, max independent set39, max clique40, integer factorization41, graph isomorphism42,43, ramsey number44, binary classification45,46, unstructured search47 and search engine ranking48. Many of these approaches3,37,38,40,41,42,43,44,45,46 recast the computational problem at hand into a problem of finding the ground state of a quantum Ising spin glass model, which is NP-complete to solve in the worst case49,50.
The computational difficulty of Ising spin glass has not only given the quantum Ising Hamiltonians the versatility for efficiently encoding many problems in NP50, but also motivated physical realization of QA using systems described by the quantum Ising model6,7,9. The notion of adiabatic quantum computing (AQC)3,37,51, which can be regarded as a particular class of QA, has further established QA in the context of quantum computation (In this work we will use the terms quantum annealing and adiabatic quantum computing synonymously). Although it is believed that even universal quantum computers cannot solve NP-hard problems efficiently in general52, there has been evidence in experimental quantum Ising systems that suggests quantum speedup over classical computation due to quantum tunneling53,54. It is then of great interest to explore more regimes where quantum annealing could offer a speedup compared with simulated annealing.
Here we consider a variant of Set Cover (SC) called Set Cover with Pairs (SCP). SC is one of Karp’s 21 NP-complete problems55 and SCP was first introduced56 as a generalization of SC. Instead of requiring each element to be covered by a single object as in SC, the SCP problem is to find a minimum subset of objects so that each element is covered by at least one pair of objects. We will present its formal definition in the Preliminaries section. SCP and its variants arise in a wide variety of contexts including Internet traffic monitoring and content distribution57, computational biology58,59 and biochemistry60. On classical computers, the SCP problem is at least as hard to approximate as SC. Specifically, its difficulty on classical computers can be manifested in the results by Breslau et al.57, which showed that no polynomial time algorithm can approximately solve Disjoint-Path Facility Location, a special case of SCP, on n objects to within a factor that is  for any ε > 0. Due to its complexity, various heuristics56 and local search algorithms60 have been proposed.
for any ε > 0. Due to its complexity, various heuristics56 and local search algorithms60 have been proposed.
In this paper we explore using quantum annealing based on Ising spin glass to solve SCP. We start by reducing SCP to finding the ground state of Ising spin glass, via integer linear programming (Theorem 1). We then simulate the adiabatic evolution of the time dependent transverse Ising Hamiltonian  which interpolates linearly between an initial Hamiltonian H0 of independent spins in uniform transverse field and a final Hamiltonian H1 that encodes an SCP instance. For randomly generated SCP instances that lead to Ising Hamiltonian constructions of up to 19 spins, we explicitly simulate the time dependent Schrödinger equation. We compute the minimum evolution time that each instance needed to accomplish 25% success probability. For benchmark purpose we also use simulate annealing to solve the instances and compare its performance with that of adiabatic evolution. Results show that the median time for yielding 25% success probablity scales as O(20.33M) for quantum annealing and O(20.21M) for simulated annealing, observing no general quantum speedup. However, the performance of quantum annealing appears to have wider range of variance from instance to instance than simulated annealing, casting hope that perhaps certain subsets of the instance could yield a quantum advantage over the classical algorithms.
which interpolates linearly between an initial Hamiltonian H0 of independent spins in uniform transverse field and a final Hamiltonian H1 that encodes an SCP instance. For randomly generated SCP instances that lead to Ising Hamiltonian constructions of up to 19 spins, we explicitly simulate the time dependent Schrödinger equation. We compute the minimum evolution time that each instance needed to accomplish 25% success probability. For benchmark purpose we also use simulate annealing to solve the instances and compare its performance with that of adiabatic evolution. Results show that the median time for yielding 25% success probablity scales as O(20.33M) for quantum annealing and O(20.21M) for simulated annealing, observing no general quantum speedup. However, the performance of quantum annealing appears to have wider range of variance from instance to instance than simulated annealing, casting hope that perhaps certain subsets of the instance could yield a quantum advantage over the classical algorithms.
Aside from the theoretical and numerical studies, we also consider the potential implementation our Hamiltonian construction on the large-scale Ising spin systems manufactured by D-Wave Systems6,7,9,14. Benchmarking the efficiency of QA is currently of significant interest. An important issue that needs to be addressed in such benchmarks is that the physical implementation of the algorithm could be affected by instance-specific features. This is manifested in the embedding61,62 of the Ising Hamiltonian construction onto the specific topology of the hardware (the Chimera graph21,61,63). Here we present a general embedding of SCP instances onto a Chimera graph that preserves the original structure of the instances and requires less qubits than the usual approach by complete graph embedding. This allows for efficient physical implementations that are untainted by ad hoc constructions that are specific to individual instances.
Preliminaries
Set Cover with Pairs
Given a ground set U and a collection S of subsets of U, which we call the cover set. Each element in S has a non-negative weight, the Set Cover (SC) problem asks to find a minimum weight subset of S that covers all elements in U. Define cover function as  where
where  , Q(s) is the set of all elements in U covered by s. Then SC can be formulated as finding a minimum weight
, Q(s) is the set of all elements in U covered by s. Then SC can be formulated as finding a minimum weight  such that
such that  . Set Cover with Pairs (SCP) can be considered as a generalization of SC in the sense that if we define the cover function such that
. Set Cover with Pairs (SCP) can be considered as a generalization of SC in the sense that if we define the cover function such that  ,
,  , i≠j, Q(i, j) is the set of elements in U covered by the pair {i, j}, then SCP asks to find a minimum subset
, i≠j, Q(i, j) is the set of elements in U covered by the pair {i, j}, then SCP asks to find a minimum subset  such that
such that  . Here we restrict to cases where each element of S has unit weight.
. Here we restrict to cases where each element of S has unit weight.
A graph G(V, E) is a set of vertices V connected by a set of edges E. A bipartite graph is defined as a graph whose set of vertices V can be partitioned into two disjoint sets V1 and V2 such that no two vertices within the same set are adjacent. We formally define SCP as the following.
Definition 1. (Set Cover with Pairs) Let U and S be disjoint sets of elements and  . Given a bipartite graph G(V, E) between U and S with E being the set of all edges, find a subset
. Given a bipartite graph G(V, E) between U and S with E being the set of all edges, find a subset  such that:
such that:
-
1
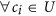 ,
, 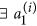 ,
,  such that
such that  and
and  . In other words, ci is covered by the pair
. In other words, ci is covered by the pair  .
. -
2
The size of the set, |A|, is minimized.
We use the notation SCP(G, U, S) to refer to a problem instance with |U| = n, |S| = m and the connectivity between U and S determined by G.
Quantum annealing, adiabatic quantum computing
In this paper we use QA as a heuristic method to solve the SCP problem. QA was proposed2 for solving optimization problems using quantum fluctuations, known as quantum tunneling, to escape local minima and discover the lowest energy state. Farhi et al.3 provide the framework for using Adiabatic Quantum Computation (AQC), which is closely related to QA, as a quantum paradigm to solve NP-hard optimization problems. The first step of the framework is to define a Hamiltonian HP whose ground state corresponds to the solution of the combinatorial optimization problem. Then, we initialize a system in the ground state of some beginning Hamiltonian HB that is easy to solve and perform the adiabatic evolution  . Here
. Here  is a time parameter. In this paper we only consider time-dependent function s(t) = t/T for total evolution time T, but in general it could be any general functions that satisfy s(0) = 0 and s(T) = 1. The adiabatic evolution is governed by the Schrödinger equation
is a time parameter. In this paper we only consider time-dependent function s(t) = t/T for total evolution time T, but in general it could be any general functions that satisfy s(0) = 0 and s(T) = 1. The adiabatic evolution is governed by the Schrödinger equation

where |ψ(t)〉 is the state of the system at any time  . Let πi(s) be the i-th instantaneous eigenstate of H(s). In other words, let
. Let πi(s) be the i-th instantaneous eigenstate of H(s). In other words, let  for any s. In particular, let |π0(s)〉 be the instantaneous ground state of H(s).
for any s. In particular, let |π0(s)〉 be the instantaneous ground state of H(s).
According to the adiabatic theorem64, for s varying sufficiently slow from 0 to 1, the state of the system |ψ(t)〉 will remain close to the true ground state |π0(s(t))〉. At the end of the evolution the system is roughly in the ground state of HP, which encodes the optimal solution to the problem. If the ground state of HP is NP-complete to find (for instance consider the case for Ising spin glass49), then the adiabatic evolution H(s) could be used as a heuristic for solving the problem.
An important issue associated with AQC is that the adiabatic evolution needs to be slow enough to avoid exciting the system out of its ground state at any point. In order to estimate the scaling of the minimum runtime T needed for the adiabatic computation, criteria based on the minimum gap between the ground state and the first excited state of H(s) is often used. However, here we do not use the minimum gap as an intermediate for estimating the runtime scaling, but instead numerically integrate the time dependent Schrödinger equation (1).
Quantum Ising model with transverse field
The Hamiltonian for an Ising spin glass on N spins can be written as

where  acts on the i-th spin with
acts on the i-th spin with  being a 2 × 2 identity matrix. hi, Jij are coefficients. The Hamiltonian is diagonal in the basis
being a 2 × 2 identity matrix. hi, Jij are coefficients. The Hamiltonian is diagonal in the basis  in the Hilbert space
in the Hilbert space  . In particular σz|0〉 = |0〉 and σz|1〉 = −|1〉. We formally define the problem of finding the ground state of an N-qubit Ising Hamiltonian in the following.
. In particular σz|0〉 = |0〉 and σz|1〉 = −|1〉. We formally define the problem of finding the ground state of an N-qubit Ising Hamiltonian in the following.
Definition 2. (Ising Hamiltonian) Given the Hamiltonian H in equation (2), find a quantum state  , where
, where  is 2N-dimensional, such that the energy
is 2N-dimensional, such that the energy  is minimized. We use the notation ISING (h, J) to refer to the problem instance where
is minimized. We use the notation ISING (h, J) to refer to the problem instance where  and
and  is a matrix such that the ij-th and the ji-th elements are equal to Jij/2. The diagonal elements of J are 0. Hence
is a matrix such that the ij-th and the ji-th elements are equal to Jij/2. The diagonal elements of J are 0. Hence  where
where  .
.
In this paper, we construct Ising Hamiltonians whose ground state encodes the solution to an arbitrary instance of the SCP problem. The physical system used for quantum annealing that we assume is identical to that of D-Wave6,7,9,14, namely Ising spin glass with transverse field

where  acts on the i-th spin. The beginning Hamiltonian HB has its hi, jij = 0 for all i, j and the final Hamiltonian HP has Δi = 0 for all i while hi and Jij depend on the problem instance at hand. We will elaborate on assigning hi and Jij coefficients in HP in Theorem 1.
acts on the i-th spin. The beginning Hamiltonian HB has its hi, jij = 0 for all i, j and the final Hamiltonian HP has Δi = 0 for all i while hi and Jij depend on the problem instance at hand. We will elaborate on assigning hi and Jij coefficients in HP in Theorem 1.
Graph minor embedding
The interactions described by the transverse Ising Hamiltonian in equation (3) are not restricted by any constrains. However, in practice the topology of interactions is always constrained to the connectivity that the hardware permits. Therefore in order to physically implement an arbitrary transverse Ising Hamiltonian, one must address the problem of embedding the Hamiltonian into the logical fabric of the hardware61,62. For convenience we define the interaction graph of an Ising Hamiltonian H of the form in equation (2) as a graph GH(VH, EH) such that each spin i maps to a distinctive element vi in VH and there is an edge between vi and vj iff Jij≠0. This definition also applies to the transverse Ising system described in equation (3). We use the term hardware graph to refer to a graph whose vertices represent the qubits in the hardware and the edges describe the allowed set of couplings in the hardware.
In Section Set Cover with Pairs we defined bipartite graphs. Here we define a complete bipartite graph Km,n as a bipartite graph where |V1| = m, |V2| = n and each vertex in V1 is connected with each vertex in V2. A graph H(W, F) is a subgraph of G(V, E) if  and
and  . It is possible that the interaction graph of the desired Ising Hamiltonian is a subgraph of the hardware connectivity graph. In this case the embedding problem can be solved by subgraph embedding, which we define as the following.
. It is possible that the interaction graph of the desired Ising Hamiltonian is a subgraph of the hardware connectivity graph. In this case the embedding problem can be solved by subgraph embedding, which we define as the following.
Definition 3. A subgraph embedding of G(V, E) into G′(V′, E′) is a mapping  such that each vertex in V is mapped to a unique vertex in V′ and if
such that each vertex in V is mapped to a unique vertex in V′ and if  then
then  .
.
In more general cases, for an arbitrary Ising Hamiltonian, a subgraph embedding may not be obtainable and we will need to embed the interaction graph into the hardware as a graph minor. Before we define minor embedding rigorously, recall that a graph is connected if for any pair of vertices u and v there is a path from u to v. A tree is a connected graph which does not contain any simple cycles as subgraphs. T is a subtree of G if T is a subgraph of G and T is a tree. We then define minor embedding as the following.
Definition 4. A minor embedding of G(V, E) in G′(V′, E′) is defined by a mapping  such that each vertex
such that each vertex  is mapped to a connected subtree Tv of G′ and if
is mapped to a connected subtree Tv of G′ and if  then there exist iu,
then there exist iu,  such that
such that  ,
,  and
and  .
.
If such a mapping ϕ exists between G and G′, we say G is a minor of G′ and we use G ≤ mG′ to denote such relationship. Our goal is to take the interaction graph GH of our Ising Hamiltonian construction and construct the mapping ϕ that embeds GH into the hardware graph as a minor.
Chimera graphs
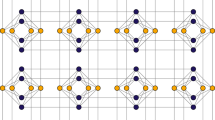
Here we specifically consider the embedding our construction into a particular type of hardware graphs used by D-Wave devices44,65 called the Chimera graphs. The basic components of this graph are 8-spin unit cells6 whose interactions form a K4,4. The K4,4 unit cells are tiled together and the 4 nodes on the left half of K4,4 are connected to their counterparts in the cells above and below. The 4 nodes on the right half of K4,4 are connected to their counterparts in the cells left and right. Furthermore, we define F(p, q, c) as a Chimera graph formed by an p × q grid of Kc,c cells. Figure 1a shows F(3, 4) as an example. Note that any Km,n with m, n ≤ c can be trivially embedded in F(p, q, c) with any p, q ≥ 1 via subgraph embedding. However, it is not clear a priori how to embed Km,n with m > c or n > c onto a Chimera graph, other than using the general embedding of an (m + n)-node complete graph and consider Km,n as a subgraph. This costs O((m + n)2) qubits in general and one may lose the intuitive structure of a bipartite graph in the embedding. One of the building blocks of our embedding for our Ising Hamiltonian construction (Section Embedding on quantum hardware) is an alternative embedding strategy for mapping any Km,n onto  as a graph minor. Our embedding costs O(mn) qubits and preserves the structure of the bipartite graph.
as a graph minor. Our embedding costs O(mn) qubits and preserves the structure of the bipartite graph.
Quantum annealing for solving SCP
From an arbitrary SCP instance to an Ising Hamiltonian construction
SCP is NP-complete most simply because Set Cover (SC) is a special case of SCP56 and a solution to SCP is clearly efficiently verifiable. Since SC is NP-complete itself, any SCP instance can be rewritten as an instance of SC with polynomial overhead. The Ising Hamiltonian construction for Set Cover is explicitly known39,50. Hence it is natural to consider using the chain of reductions from SCP to SC and then from SC to ISING (Definition 2). If we recast each SCP(G, U, S) with |S| = m into an SC instance with a cover set of size O(m2). Using the construction by Lucas50 we have an Ising Hamiltonian

where Vi is the i-th cover set in the SC instance. Since the cover set {Vi} is possibly of size up to O(m2), this leads to the Ising Hamiltonian in equation (4) costing O(nm2) qubits.
Here we present an alternative Ising Hamiltonian construction for encoding the solution to any SCP instance. We state the result precisely as Theorem 1 below. The qubit cost of our construction is comparable to that of Lucas. However, in Section Embedding on quantum hardware we argue that our construction affords more advantages in terms of embedding.
Theorem 1. Given an instance of the Set Cover with Pairs Problem SCP(G, U, S) as in Definition 1, there exists an efficient (classical) algorithm that computes an instance of the Ising Hamiltonian ground state problem ISING(h, J) with  and
and  where the number of qubits involved in the Hamiltonian is M = O(nm2) with n = |U| and m = |S|.
where the number of qubits involved in the Hamiltonian is M = O(nm2) with n = |U| and m = |S|.
Proof. First, we recast an SCP instance to an instance of integer programming, which is NP-hard in the worst case. Then, we convert the integer programming problem to an instance of the ISING problem. Recall Definition 1 of an SCP(G, U, S) instance, where G(V, E) is a graph on the vertices V = U ∪ S. For each pair  define a set
define a set  . The problem can be recast as an integer program by
. The problem can be recast as an integer program by




We have introduced the variable si to indicate whether fi is chosen for the cover A ⊆ S (si = 1 means that fi is chosen, otherwise si = 0). We have also introduced the auxiliary variable tij to indicate whether fi and fj are both chosen. Hence, constraint LP.1 ensures that each element ck ∈ U is covered by at least one pair in S. LP.2 ensures that a pair of elements in S cannot cover any ck ∈ U unless both elements are chosen.
To convert the integer program to an ISING instance, we first convert the constraints into expressions of logical operations. LP.1 can be rewritten as

LP.2 can be translated to a truth table for the binary operation involving tij and si(sj) where only the entry  evaluates to 0 and the other three entries evaluate to 1. Using the following Hamiltonians we could translate the logic operations ∨, ∧ and ≤ into the ground states of Ising model, see ref. 66 for more details.
evaluates to 0 and the other three entries evaluate to 1. Using the following Hamiltonians we could translate the logic operations ∨, ∧ and ≤ into the ground states of Ising model, see ref. 66 for more details.

Note that H≤(s1, s2) is essentially  . In other words we are penalizing the only 2-bit string s1s2 that violates the constraint s1 ≤ s2. The ground state subspace of H∨ is spanned by
. In other words we are penalizing the only 2-bit string s1s2 that violates the constraint s1 ≤ s2. The ground state subspace of H∨ is spanned by  . Similarly, the ground state subspace of H∧ is spanned by
. Similarly, the ground state subspace of H∧ is spanned by  and that of H≤ spanned by
and that of H≤ spanned by  .
.
By linearly combining the above constraint Hamiltonians, we can enforce multiple constraints to hold at the same time. For example, the statement  can be decomposed as simultaneously ensuring
can be decomposed as simultaneously ensuring  ,
,  and z = 1. In other words we have used auxiliary variables y and z to transform the constraint
and z = 1. In other words we have used auxiliary variables y and z to transform the constraint  , which involves a clause
, which involves a clause  of three variables, to a set of constraints involving only clauses of two variables. Then, the Ising Hamiltonian
of three variables, to a set of constraints involving only clauses of two variables. Then, the Ising Hamiltonian  has its ground state spanned by states
has its ground state spanned by states  with s1, s2 and s3 satisfying
with s1, s2 and s3 satisfying  . The third term in H ensures that z = 1 by penalizing states with
. The third term in H ensures that z = 1 by penalizing states with  .
.
Therefore, we can translate (5) to an Ising Hamiltonian. For a fixed k, the constraint (5) takes the form of  where each
where each  and
and  . Similarly to the example above, we introduce Nk − 1 auxiliary variables
. Similarly to the example above, we introduce Nk − 1 auxiliary variables  ,
,  such that
such that

Thus,  . In order to ensure the first constrain holds, it is needed to ensure that
. In order to ensure the first constrain holds, it is needed to ensure that  . Then we could write down the corresponding Ising Hamiltonian for the constraint as
. Then we could write down the corresponding Ising Hamiltonian for the constraint as

The last term is meant to make sure that  in the ground state of Hk. Therefore the Hamiltonian whose ground state subspace is spanned by all states that obey both of the constraints in the integer program (5) can be written as
in the ground state of Hk. Therefore the Hamiltonian whose ground state subspace is spanned by all states that obey both of the constraints in the integer program (5) can be written as

The target function  which we seek to minimize can be directly mapped to an Ising Hamiltonian
which we seek to minimize can be directly mapped to an Ising Hamiltonian  . This is because we would like to essentially minimize the number of 1’s in the set of si values and penalize choices with more 1’s. Therefore the final Hamiltonian whose ground state contains the solution to the original SCP instance becomes
. This is because we would like to essentially minimize the number of 1’s in the set of si values and penalize choices with more 1’s. Therefore the final Hamiltonian whose ground state contains the solution to the original SCP instance becomes

for some weight factor α.
We now estimate the overhead for the mapping. Htarg acts on |S| = m qubits. In Hcons, H≤ acts on O(m2) qubits, since there are O(m2) variables tij. Each Hk in Hcons requires Nk = O(m2) qubits. There are in total |U| = n of the Hk terms, which gives O(nm2) qubits in total. □
Example
Consider the SCP instance shown in Fig. 2a. With the mapping presented in Theorem 1, we arrive at an Ising instance ISING (h, J) where α = 1/4 in (10) and h, J are presented in Supplementary Material Details of the example SCP instance. The ground state subspace of the Hamiltonian in (2) with hi and Jij coefficients defined above, restricted to the si elements is spanned by  . This corresponds to A = {f1, f4}, the solution to the SCP instance. Figure 2b illustrates the interaction graph of the spins in the Ising Hamiltonian that corresponds to the SCP instance.
. This corresponds to A = {f1, f4}, the solution to the SCP instance. Figure 2b illustrates the interaction graph of the spins in the Ising Hamiltonian that corresponds to the SCP instance.
Example of converting an SCP instance to Ising Hamiltonian.
(a) The SCP instance. Here  and
and  . The solution is the set
. The solution is the set  . The circles represent the covering set elements S and the squares are the ground elements U. (b) The interaction of Ising instance HSCP converted from the SCP instance in (a). Every node corresponds to a qubit. The si’s are the output bits that correspond to the covering set elements S. The others are auxiliary variables. Every edge represents an interaction term between the corresponding spins. Here we do not show the 1-local terms in our construction of HSCP (for example the terms in Htarg for enforcing the minimization of the target function). The bold dashed black line exemplifies the edges between the
. The circles represent the covering set elements S and the squares are the ground elements U. (b) The interaction of Ising instance HSCP converted from the SCP instance in (a). Every node corresponds to a qubit. The si’s are the output bits that correspond to the covering set elements S. The others are auxiliary variables. Every edge represents an interaction term between the corresponding spins. Here we do not show the 1-local terms in our construction of HSCP (for example the terms in Htarg for enforcing the minimization of the target function). The bold dashed black line exemplifies the edges between the  nodes and the si nodes, which come from the constraints
nodes and the si nodes, which come from the constraints  and
and  for each pair
for each pair  that covers ck. Each of the inequality constraints is enforced by a H≤ term in (6). The bold triangle exemplifies the H∨ constraints in (6) that are used to enforce the logical relationship between the
that covers ck. Each of the inequality constraints is enforced by a H≤ term in (6). The bold triangle exemplifies the H∨ constraints in (6) that are used to enforce the logical relationship between the  variables and the auxiliary variables as shown in (7). The areas marked by
variables and the auxiliary variables as shown in (7). The areas marked by  ,
,  etc outline the structure of the Ising Hamiltonian that is relevant in the discussion of hardware embedding.
etc outline the structure of the Ising Hamiltonian that is relevant in the discussion of hardware embedding.
Numerical simulation of quantum annealing
In order to test the time complexity of using quantum annealing to solve SCP instances via the construction in Theorem 1, we generate random instances of SCP that lead to Ising Hamiltonian HSCP of  spins. In Definition 1 we use a bipartite graph between the ground state U of size n and the cover set S of size m to describe an SCP instance. For fixed n and m, there are in total 2mn such possible bipartite graphs (if we consider each bipartite graph as a subgraph of Km,n and count the cardinality of the power set of the edges of Km,n). Therefore to generate random bipartite graphs we only need to flip mn fair coins to uniformly choose from all possibile bipartite graphs between U and S. However, we would like to exclude the bipartite graphs where some element of S is not connected to any element in U. These “dummy nodes” are not pertinent to the computational problem at hand and should be removed from consideration before converting the SCP instance to an Ising Hamiltonian HSCP. We thus use a scheme for generating random instances of SCP without dummy nodes as described in Algorithm 1. Under the constraint that no dummy element in S is allowed, there are in total (2n − 1)m possible bipartite graphs. In Supplementary Material Proof of correctness for Algorithm 1 we rigorously show that Algorithm 1 indeed samples uniformly among the (2n − 1)m possible “dummy-free” bipartite graphs.
spins. In Definition 1 we use a bipartite graph between the ground state U of size n and the cover set S of size m to describe an SCP instance. For fixed n and m, there are in total 2mn such possible bipartite graphs (if we consider each bipartite graph as a subgraph of Km,n and count the cardinality of the power set of the edges of Km,n). Therefore to generate random bipartite graphs we only need to flip mn fair coins to uniformly choose from all possibile bipartite graphs between U and S. However, we would like to exclude the bipartite graphs where some element of S is not connected to any element in U. These “dummy nodes” are not pertinent to the computational problem at hand and should be removed from consideration before converting the SCP instance to an Ising Hamiltonian HSCP. We thus use a scheme for generating random instances of SCP without dummy nodes as described in Algorithm 1. Under the constraint that no dummy element in S is allowed, there are in total (2n − 1)m possible bipartite graphs. In Supplementary Material Proof of correctness for Algorithm 1 we rigorously show that Algorithm 1 indeed samples uniformly among the (2n − 1)m possible “dummy-free” bipartite graphs.

For each randomly generated instance from Algorithm 1 we construct an Ising Hamiltonian HSCP according to Theorem 1. We then perform a numerical simulation of the time dependent Schrödinger equation (1) from time t = 0 to t = T with time step Δt = 1 and the time dependent Hamiltonian defined as

where HSCP is defined in equation (10). Here because of the construction of HSCP, our total Hamiltonian H(s(t)) acts not only on the spins  indicating our choice of elements in the cover set S, but also auxiliary variables
indicating our choice of elements in the cover set S, but also auxiliary variables  and
and  , for which we use t and x to denote their respective collections. Our initial state is the ground state of HB, namely
, for which we use t and x to denote their respective collections. Our initial state is the ground state of HB, namely

To obtain the final state  where T is some positive integer, we use the ode45 subroutine of MATLAB under default settings to numerically integrate Schrödinger equation to obtain
where T is some positive integer, we use the ode45 subroutine of MATLAB under default settings to numerically integrate Schrödinger equation to obtain  from
from  and then use
and then use  as an initial state to obtain
as an initial state to obtain  in the same fashion and so on. We define the success probability p as a function of the total annealing time T as
in the same fashion and so on. We define the success probability p as a function of the total annealing time T as  where Π is a projector onto the subspace spanned by states with s being a solution of the original SCP instance. Using binary search we determine the minimum time T* to achieve
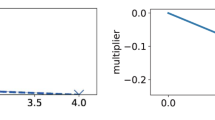
where Π is a projector onto the subspace spanned by states with s being a solution of the original SCP instance. Using binary search we determine the minimum time T* to achieve  for each instance of SCP. Figure 3 shows the distribution of T* for SCP instances that lead to Ising Hamiltonians HSCP of the same sizes, as well as how the median annealing time scales as a function of number of spins M. Results show that for instances with M up to 19, the median annealing time scales roughly as O(20.31M).
for each instance of SCP. Figure 3 shows the distribution of T* for SCP instances that lead to Ising Hamiltonians HSCP of the same sizes, as well as how the median annealing time scales as a function of number of spins M. Results show that for instances with M up to 19, the median annealing time scales roughly as O(20.31M).
Plot of the optimal quantum annealing time T* versus the number of spins involved in the construction of HSCP.
Here we fit the logarithm of median T* with a straight line. The size M of our Ising systems ranges from 3 to 19. From the fitting function we observe that the annealing time scales as roughly O(20.31M). We also provide on the bottom plot the number of instances for each M.
Numerical experiment with Simulated Annealing
Simulated annealing, first introduced three decades ago67, has been widely used as a heuristic for handling hard combinatorial optimization problems. It is especially of interest as a benchmark for quantum annealing34,35,36 because of similarities between the two algorithms. While quantum annealing employs quantum tunneling to escape from local minima, simulated annealing relies on thermal excitation to avoid being trapped in local minima. The general procedure we adopt for simulated annealing to approach the ground state of an Ising spin glass can be summarized as the following68:
-
1
Repeat R times the following:
-
a
Initialize s ← s0 randomly;
-
b
Perform S times the following: (let
 index the steps)
index the steps)
-
i
Set the temperature
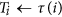 ;
; -
ii
Perform a sweep on si to obtain s′; (a sweep is a sequence of steps each of which randomly selects a spin and flips its state, so that on average each spin is flipped once during a sweep)
-
iii
With probability
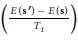 , let
, let  . Otherwise let
. Otherwise let 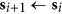 .
.
-
1
Return sS as the answer.
For the purpose of comparison we also used simulated annealing to solve the same set of instances generated by Algorithm 1 for testing quantum annealing. The program implementation that we use is built by Isakov et al.68, which is a highly optimized implementation of simulated annealing with care taken to exploit the structures of the interaction graph, such as being bipartite and of bounded degree. Here we use the program’s most basic realization of single-spin code for general interactions with magnetic field on an interaction graph of any degree.
As mentioned by Isakov et al., to improve the solution returned by simulated annealing, one could increase either the number of sweeps S or number of repetitions R in the implementation, or both of them. However, note that the total annealing time is proportional to the product  and there is a trade-off between S and R. For a fixed number of sweeps S let the success probability (i.e. the fraction of si that is satisfactory) be w(S). In order to achieve a constant success probability p (say 25%, which is what we use here), we need at least
and there is a trade-off between S and R. For a fixed number of sweeps S let the success probability (i.e. the fraction of si that is satisfactory) be w(S). In order to achieve a constant success probability p (say 25%, which is what we use here), we need at least  repetitions. Hence the total time of simulated annealing can be written as
repetitions. Hence the total time of simulated annealing can be written as

In general w(S) increases as S increases, leading to a decrease in R. We numerically investigate this with an Ising system of N = 17 spins generated from an SCP instance via the construction in Theorem 1. We plot the annealing time T versus S in Fig. 4a. For each SCP instance with the number of spin M we compute the optimal S* such that  is the optimized runtime (Fig. 4a). We further explore how the optimal runtime T* scales as a function of the number of spins M. As shown in Fig. 4b, a linear fit on a semilog plot shows that roughly
is the optimized runtime (Fig. 4a). We further explore how the optimal runtime T* scales as a function of the number of spins M. As shown in Fig. 4b, a linear fit on a semilog plot shows that roughly  .
.
(a) Plot of annealing time T versus number of sweeps S using the simulated annealing implementation68 on an Ising Hamiltonians of 17 spins constructed from an SCP instance. We use the default settings for all parameters other than S and R. Also we mark the optimal runtime T*. (b) Plot of optimized annealing time T* versus the number of spins involved in the Ising Hamiltonian HSCP corresponding to randomly generated SCP instances according to Algorithm 1. We also provide on the bottom plot the number of instances for each M.
The units of time used for both Fig. 4a,b are arbitrary and thus do not support a point-to-point comparison. But the scaling difference seems apparent. For quantum annealing we restrict to systems of at most 19 spins due to computational limitations faced in representing the full Ising Hamiltonian when numerically integrating the time-dependent Schrödinger equation (1).
Although there is no quantum speedup observed in terms of median runtime over all randomly generated instances of the same size, we notice that for a fixed number of spins M the performances of both quantum annealing and simulated annealing are sensitive to the specific instance of Ising Hamiltonian HSCP than simulated annealing. This can be seen by considering at the same time the quantum annealing results in Fig. 3 and the test results for simulated annealing shown in Fig. 4b. One could then speculate that perhaps by focusing on a specific subset of SCP instances could yield a quantum advantage.
Embedding on quantum hardware
In this section we deal with the physical realization of quantum annealing for solving SCP instances using D-Wave type hardwares. There are mainly two aspects62,69 of this effort: 1) The embedding problem62, namely embedding the interaction graph of the Ising Hamiltonian construction HSCP as a graph minor of a Chimera graph (refer to Section Graph minor embedding for definitions of the graph terminologies). 2) The parameter setting problem69, namely assigning the strengths of the couplings and local magnetic fields for embedded graph on the hardware, in a way that minimizes the energy scaling (or control precision) required for implementing the embedding. Here we focus on the former issue.
We start with an observation on the structures of HSCP. For any instance SCP(G, U, S) according to Definition 1, the interaction graph ISCP(G,U,S) of the corresponding Ising Hamiltonian HSCP can be regarded as a union of n subgraphs, namely  . Each subgraph G(i) is associated with an element of the ground set
. Each subgraph G(i) is associated with an element of the ground set  as in Fig. 2a. Each G(i) could be further partitioned into two parts,
as in Fig. 2a. Each G(i) could be further partitioned into two parts,  and
and  . For any k,
. For any k,  is a bipartite graph between
is a bipartite graph between  and
and  .
.  essentially describes the interaction between the auxiliary variables
essentially describes the interaction between the auxiliary variables  and
and  as described in equation (7). In Fig. 2b we illustrate such partition using the example from Fig. 2b. Our goal is then to show constructively that ISCP(G,U,S) ≤ mF(f1, f2, c) for some f1, f2 that depend on m, n and c = 4, which describes the Chimera graph realized by D-Wave hardware (Fig. 1a).
as described in equation (7). In Fig. 2b we illustrate such partition using the example from Fig. 2b. Our goal is then to show constructively that ISCP(G,U,S) ≤ mF(f1, f2, c) for some f1, f2 that depend on m, n and c = 4, which describes the Chimera graph realized by D-Wave hardware (Fig. 1a).
It is known61 that one could embed a complete graph on cm + 1 nodes onto Chimera graph  . Since any n-node graph is a subgraph of the n-node complete graph, in principle any n-node graph can be embedded onto Chimera graphs of size O(n2) using the complete graph embedding. A downside of this approach is that it may fail to embed many graphs that are in fact embeddable61. Also, using embeddings based on complete graph embeddings will likely lose the intuition on the structure of the original graph. For graphs with specific structures, such as bipartite graphs one may be able to find an embedding that is also in some sense structured. We show in the following Lemma an embedding for any complete bipartite graph Kp,q onto a Chimera graph. The ability to do so enables us to embed any bipartite graph onto a Chimera graph.
. Since any n-node graph is a subgraph of the n-node complete graph, in principle any n-node graph can be embedded onto Chimera graphs of size O(n2) using the complete graph embedding. A downside of this approach is that it may fail to embed many graphs that are in fact embeddable61. Also, using embeddings based on complete graph embeddings will likely lose the intuition on the structure of the original graph. For graphs with specific structures, such as bipartite graphs one may be able to find an embedding that is also in some sense structured. We show in the following Lemma an embedding for any complete bipartite graph Kp,q onto a Chimera graph. The ability to do so enables us to embed any bipartite graph onto a Chimera graph.
Lemma 1. For any positive integers p, q and c,  .
.
Proof. By the definition of graph minor embedding in Section Graph minor embedding, it suffices to construct a mapping  where each v in Fp,q is mapped to a tree Tv in
where each v in Fp,q is mapped to a tree Tv in  and each edge e = (u, v) in Kp,q is mapped to an edge
and each edge e = (u, v) in Kp,q is mapped to an edge  with
with  and
and  .
.
Let  label the nodes on one side of Kp,q and
label the nodes on one side of Kp,q and  label the nodes in the other. Using the labelling scheme on the nodes of Chimera graphs introduced in Section Chimera graphs and Fig. 1b, we define our mapping
label the nodes in the other. Using the labelling scheme on the nodes of Chimera graphs introduced in Section Chimera graphs and Fig. 1b, we define our mapping  as
as

where  maps an edge (u, v) in Kp,q to the Chimera graph. If we choose the edges in the Chimera graph properly, it could be checked that
maps an edge (u, v) in Kp,q to the Chimera graph. If we choose the edges in the Chimera graph properly, it could be checked that  is a subgraph of
is a subgraph of  .□
.□
In Fig. 5 we show an example of embedding K7,10 into F(3, 2, 4). A natural corollary of Lemma 1 is that any bipartite graph between p and q nodes can be minor embedded in  . We are then prepared to handle embedding the
. We are then prepared to handle embedding the  parts of the interaction graphs of HSCP, which are but bipartite graphs (see Fig. 2b for example).
parts of the interaction graphs of HSCP, which are but bipartite graphs (see Fig. 2b for example).
We then proceed to treat the  parts of the interaction graph. The connectivity of
parts of the interaction graph. The connectivity of  is completely specified by (7). To describe such connectivity we define a family of graph
is completely specified by (7). To describe such connectivity we define a family of graph  as
as  where
where  and
and  are two disjoint sets of nodes, the former representing the intermediate variables
are two disjoint sets of nodes, the former representing the intermediate variables  and the latter representing the xk variables in equation (7). The set of edges takes the form
and the latter representing the xk variables in equation (7). The set of edges takes the form

In Fig. 6 we show an example of L10. For any  , let rk be the number of pairs
, let rk be the number of pairs  that cover k. Then
that cover k. Then  . Hence in order to show that we could embed any
. Hence in order to show that we could embed any  onto a Chimera graph, it suffices to show that we can embed any Ln onto a Chimera graph. We show this in the following Lemma for c = 4.
onto a Chimera graph, it suffices to show that we can embed any Ln onto a Chimera graph. We show this in the following Lemma for c = 4.
Lemma 2. For any positive integer n,  where we restrict to c = 4.
where we restrict to c = 4.
Proof. Similar to Lemma 1, we construct a mapping  where we fix c = 4. Following the notation for nodes in Ln in Fig. 6 and the notation for nodes in
where we fix c = 4. Following the notation for nodes in Ln in Fig. 6 and the notation for nodes in  in Fig. 1b, we construct μ as
in Fig. 1b, we construct μ as

where  and
and  are defined as
are defined as


With the vertex mapping μn, a mapping of edges in Ln onto the Chimera graph  is easy to find.
is easy to find.
In Fig. 6 we show an example of embedding L10 onto F(5, 2, 4). We could then proceed to embed the interaction graph ISCP(G,U,S), such as the one shown in Fig. 2b, in a Chimera graph. Specifically, we state the following theorem.
Theorem 2. For any instance  with
with  and
and  ,
,  where
where  ,
,  and c = 4 is a constant.
and c = 4 is a constant.
Proof. Our embedding combines ideas from Lemma 1 and 2. We modify the mapping ϕp,q constructed in Lemma 1 to produce a new mapping θp,q that produces more spacing between the embedded nodes (see for example  and
and  in Fig. 7):
in Fig. 7):

Let  denote a mapping μ described in Lemma 2 that maps the upper left node (Fig. 6) t1 to
denote a mapping μ described in Lemma 2 that maps the upper left node (Fig. 6) t1 to  instead of
instead of  . The rest of the mapping then proceeds from
. The rest of the mapping then proceeds from  . In other words,
. In other words,  is the mapping μ that is shifted by p − 1 cells to the right and q − 1 cells below. Trivially
is the mapping μ that is shifted by p − 1 cells to the right and q − 1 cells below. Trivially  . Similarly we define
. Similarly we define  as the shifted embedding under θp,q where
as the shifted embedding under θp,q where  . Recall that for any ground set element
. Recall that for any ground set element  , rk is the number of pairs in S that covers ck. We could then specify the embedding from
, rk is the number of pairs in S that covers ck. We could then specify the embedding from  onto
onto  as
as

where  is the total number of rows of cells occupied by the embedded graphs for handling the ground elements c1 through cj−1. In total Φ(ISCP(G,U,S)) will occupy
is the total number of rows of cells occupied by the embedded graphs for handling the ground elements c1 through cj−1. In total Φ(ISCP(G,U,S)) will occupy  rows and
rows and  columns.□
columns.□
In Fig. 7 we show an embedding  of the example instance in Fig. 2 onto F(4, 4, 4). Note that our embedding preserves the original structure of the interaction graph as shown in Fig. 2b. Furthermore, note that the interaction graph ISCP(G,U,S) has
of the example instance in Fig. 2 onto F(4, 4, 4). Note that our embedding preserves the original structure of the interaction graph as shown in Fig. 2b. Furthermore, note that the interaction graph ISCP(G,U,S) has  nodes. Using the complete graph embedding requires
nodes. Using the complete graph embedding requires  qubits. For the same reason, the construction of Ising Hamiltonian described in equation (4) is likely going to cost O(nm4) in the worst case of embeding in a Chimera graph since the interaction graph of the Hamiltonian could involve complete graphs of size O(m2) due to the square term HA. By comparison our embedding costs
qubits. For the same reason, the construction of Ising Hamiltonian described in equation (4) is likely going to cost O(nm4) in the worst case of embeding in a Chimera graph since the interaction graph of the Hamiltonian could involve complete graphs of size O(m2) due to the square term HA. By comparison our embedding costs  qubits and preserves the structure of the original instance, which affords slightly more advantage for scalable physical implementations.
qubits and preserves the structure of the original instance, which affords slightly more advantage for scalable physical implementations.
Discussion
Our interest in SCP is largely motivated by its important applications in various areas57,58,59,60. We have shown a complete pipeline of reductions that converts an arbitrary SCP instance to an interaction graph on a D-Wave type hardware based on Chimera graphs, in a way that preserves the structure of the instance throughout (Figs 2b and 7) and is more qubit efficient than the usual approach by complete graph embedding. Although no quantum speedup is observed at this stage based on comparison of median annealing times, the large variance of runtimes observed in Fig. 3a from instance to instance might suggest that specific subsets of instances could provide quantum speedup. Of course, a clearer understanding of the performance of quantum annealing on solving SCP could only be brought forth by both scaling up the numerical simulation of the quantum annealing process to include instances with larger number of spins and actual experimental implementation of the quantum annealing process. Both of them are of interest to us in our future work.
Additional Information
How to cite this article: Cao, Y. et al. Solving Set Cover with Pairs Problem using Quantum Annealing. Sci. Rep. 6, 33957; doi: 10.1038/srep33957 (2016).
References
Finnila, A. B., Gomez, M. A., Sebenik, C., Stenson, C. & Doll, J. D. Quantum annealing: A new method for minimizing multidimensional functions. Chemical Physics Letter 219, 343–348 (1994).
Kadowaki, T. & Nishimori, H. Quantum annealing in the transverse ising model. Physical Review E 58, 5355 (1998).
Farhi, E. et al. A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem. Science 292, 472–475 (2001).
Das, A. & Chakrabarti, B. K. Quantum annealing and related optimization methods vol. 679 (Springer Science & Business Media, 2005).
Das, A. & Chakrabarti, B. K. Quantum annealing and analog quantum computation. Review of Modern Physics 80, 1061 (2008).
Harris, R. et al. Experimental investigation of an eight-qubit unit cell in a superconducting optimization processor. Physical Review B 82, 024511 (2010).
Johnson, M. W. et al. Quantum annealing with manufactured spins. Nature 473, 194–198 (2011).
Bapst, V., Foini, L., Krzakala, F., Somerjian, G. & Zamponi, F. The quantum adiabatic algorithm applied to random optimization problems: The quantum spin glass perspective. Physics Reports 523, 127–205 (2013).
Dickson, N. G. et al. Thermally assisted quantum annealing of a 16-qubit problem. Nature Communications 4, 1903 (2013).
Boixo, S. et al. Evidence for quantum annealing with more than one hundred qubits. Nature Physics 10, 218–224 (2014).
McGeoch, C. C. & Wang, C. Experimental evaluation of an adiabiatic quantum system for combinatorial optimization. In Proceedings of the ACM International Conference on Computing Frontiers (New York, USA, 2013).
Dash, S. A note on QUBO instances defined on Chimera graphs. ArXiv:1306.1202 [math.OC] (2013).
Boixo, S., Albash, T., Spedalieri, F. M., Chancellor, N. & Lidar, D. A. Experimental signature of programmable quantum annealing. Nature Communications 4, 3067 (2013).
Lanting, T. et al. Entanglement in a quantum annealing processor. Physical Review X 4, 021041 (2014).
Santra, S., Quiroz, G., Steeg, G. V. & Lidar, D. MAX 2-SAT with up to 108 qubits. New Journal of Physics 16, 045006 (2014).
Rønnow, T. F. et al. Defining and detecting quantum speedup. Science 345, 420 (2014).
Vinci, W. et al. Hearing the shape of the ising model with a programmable superconducting-flux annealer. Scientific Report 4, 5703 (2014).
Shin, S. W., Smith, G., Smolin, J. A. & Vazirani, U. How “quantum” is the D-Wave machine? ArXiv:1401.7087 [quant-ph] (2014).
Albash, T., Vinci, W., Mishra, A., Warburton, P. A. & Lidar, D. A. Consistency tests of classical and quantum models for a quantum annealer. Physical Review A 91, 042314 (2015).
McGeoch, C. In Adiabatic Quantum Computation and Quantum Annealing: Theory and Practice. 2014 (Morgan & Claypool).
Venturelli, D. et al. Quantum optimization of fully-connected spin glasses. Physical Review X 5, 031040 (2015).
Vinci, W., Albash, T., Paz-Silva, G., Hen, I. & Lidar, D. A. Quantum annealing correction with minor embedding. Physical Review A 92, 042310 (2015).
Albash, T., Rønnow, T. F., Troyer, M. & Lidar, D. A. Reexamining classical and quantum models for the D-Wave One processor. The European Physical Journal Special Topics 224, 111 (2015).
King, A. D. & McGeoch, C. C. Algorithm engineering for a quantum annealing platform. ArXiv:1410.2628 [cs.DS] (2014).
Crowley, P. J. D., Duric, T., Vinci, W., Warburton, P. A. & Green, A. G. Quantum and classical in adiabatic computation. Physical Review A 90, 042317 (2014).
Hen, I. et al. Probing for quantum speedup in spin glass problems with planted solutions. Physical Review A 92, 042325 (2015).
Steiger, D. S., Rønnow, T. F. & Troyer, M. Heavy tails in the distribution of time-to-solution for classical and quantum annealing. Physical Review Letters 115, 230501 (2015).
Bauer, B., Wang, L., Pižorn, I. & Troyer, M. Entanglement as a resource in adiabatic quantum optimization (2015).
Albash, T., Hen, I., Spedalieri, F. M. & Lidar, D. A. Reexamination of the evidence for entanglement in the d-wave processor. Physical Review A 92, 062328 (2015).
Katzgraber, H. G., Hamze, F., Zhu, Z., Ochoa, A. J. & Munoz-Bauza, H. Seeking quantum speedup through spin glasses: The good, the bad and the ugly. Physical Review X 5, 031026 (2015).
Chancellor, N., Szoke, S., Vinci, W., Aeppli, G. & Warburton, P. A. Maximum-entropy inference with a programmable annealer. Scientific Report 22318 (2016).
Perdomo-Ortiz, A., O’Gorman, B., Fluegemann, J., Biswas, R. & Smelyanskiy, V. N. Determination and correction of persistent biases in quantum annealers arXiv:1503.05679 [quant–ph] (2015).
Vinci, W., Albash, T. & Lidar, D. A. Nested quantum annealing correction arXiv:1511.07084 [quant–ph] (2015).
Farhi, E., Goldstone, J. & Gutmann, S. Quantum adiabatic evolution algorithms versus simulated annealing. MIT-CTP-3228 (2002).
Santoro, G. E., Martoňák, R., Tosatti, E. & Car, R. Theory of quantum annealing of an Ising spin glass. Science 295, 2427–2430 (2002).
Heim, B., Rønnow, T. F., Isakov, S. V. & Troyer, M. Quantum versus classical annealing of ising spin glasses. Science 348, 215–217 (2014).
Farhi, E., Goldstone, J., Gutmann, S. & Sipser, M. Quantum computation by adiabatic evolution. MIT-CTP-2936 (2000).
Farhi, E., Goldstone, J. & Gutmann, S. A numerical study of the performance of a quantum adiabatic evolution algorithm for satisfiability. MIT-CTP-3006 (2000).
Choi, V. Adiabatic quantum algorithms for the NP-complete Maximum-Weight Independent set, Exact Cover and 3SAT problems. ArXiv:1004.2226 (2010).
Childs, A. M., Farhi, E., Goldstone, J. & Gutmann, S. Finding cliques by quantum adiabatic evolution. Quantum Information and Computation 2, MIT-CTP #3067 (2002).
Peng, X. et al. Quantum adiabatic algorithm for factorization and its experimental implementation. Physical Review Letters 101, 220405 (2008).
Hen, I. & Young, A. P. Solving the graph-isomorphism problem with a quantum annealer. Physical Review A 86, 042310 (2012).
Gaitan, F. & Clark, L. Graph isomorphism and adiabatic quantum computing. Physical Review A 89, 022342 (2014).
Bian, Z., Chudak, F., Macready, W. G., Clark, L. & Gaitan, F. Experimental determination of ramsey numbers. Physical Review Letters 111, 130505 (2013).
Neven, H., Denchev, V. S., Rose, G. & Macready, W. G. Training a binary classifier with the quantum adiabatic algorithm. ArXiv:0811.0416 (2008).
Denchev, V. S., Ding, N., Vishwanathan, S. & Neven, H. Robust classification with adiabatic quantum optimization. ArXiv:1205.1148 (2012).
Roland, J. & Cerf, N. J. Quantum search by local adiabatic evolution. Physical Review A 65, 042308 (2002).
Garnerone, S., Zanardi, P. & Lidar, D. A. Adiabatic quantum algorithm for search engine ranking. Physical Review Letters 108, 230506 (2012).
Barahona, F. On the computational complexity of ising spin glass models. Journal of Physics A: Mathematical and General 15, 3241, URL http://stacks.iop.org/0305-4470/15/i=10/a=028 (1982).
Lucas, A. Ising formulations of many NP problems. ArXiv:1302.5843 (2013).
Crosson, E., Farhi, E., Lin, C. Y.-Y., Lin, H.-H. & Shor, P. Different strategies for optimization using the quantum adiabatic algorithm. ArXiv:1401.7320 (2014).
Aaronson, S. BQP and the polynomial hierarchy. Proceedings of the forty-second ACM Symposium on Theory of Computing (STOC) 141–150 (2010).
Nagaj, D., Somma, R. D. & Kieferova, M. Quantum Speedup by Quantun Annealing. Phys. Rev. Lett. 109, 050501 (2012).
Denchev, V. S. et al. What is the computational value of finite range tunneling? ArXiv:1512.02206 (2015).
Karp, R. M. Reducibility among Combinatorial Problems: Proceedings of a symposium on the Complexity of Computer Computations 85–103 (1972).
Hassin, R. & Segev, D. The Set Cover with Pairs Problem. Lecture Notes in Computer Science 3821, 164–176 (2005).
Breslau, L. et al. Disjoint-path Facility Location: Theory and Practice. Proceedings of the Thirteenth Workshop on Algorithm Engineering and Experiments (ALENEX) 60–74 (2011).
Lancia, G., Pinotti, C. M. & Rizzi, R. Haplotyping populations by pure parsimony: Complexity, exact and approximation algorithms. INFORMS Journal on Computing 16, 348–359 (2004).
Wang, I.-L. & Yang, H.-E. Haplotyping populations by pure parsimony based on compatible genotypes and greedy heuristics. Applied Mathematics and computation 217, 9798–9809 (2011).
Gonçalves, L. B., de Lima Martins, S., Ochi, L. S. & Subramanian, A. Exact and heuristic approaches for the set cover with pairs problem. Optimization Letters 6, 641–653 (2012).
Klymko, C., Sullivan, B. D. & Humble, T. S. Adiabatic quantum programming: Minor embedding with hard faults. ArXiv:1210.8395 [quant-ph] (2012).
Choi, V. Minor-embedding in adiabatic quantum computation: II. Minor-universal graph design. Quantum Information Processing 10, 343–353 (2011).
Bian, Z. et al. Discrete optimization using quantum annealing on sparse ising models. Frontiers in Physics 2 (2014).
Messiah, A. Quantum Mechanics Volume 2 (North-Holland: Publishing Company,, 1962).
Perdomo-Ortiz, A., Dickson, N., Drew-Brook, M., Rose, G. & Aspuru-Guzik, A. Finding low-energy conformations of lattice protein models by quantum annealing. Scientific Reports 2 (2012).
Biamonte, J. D. Nonperturbative k-body to two-body commuting conversion hamiltonians and embedding problem instances into ising spins. Physical Review A 77, 052331 (2008).
Kirkpatrick, S., Gelatt, C. D. & Vecchi, M. P. Optimization by simulated annealing. Science 220, 671–680 (1983).
Isakov, S. V., Zintchenko, I. N., Ronnow, T. F. & Troyer, M. Optimised simulated annealing for ising spin glasses. Computer Physics Communications, 192 265–271 (2015).
Choi, V. Minor-embedding in adiabatic quantum computation: I. The Parameter setting problem. Quantum Information Processing 7, 193–209 (2008).
Acknowledgements
The authors thank Sergei Isakov for helpful discussions on the simulated annealing code and Howard J. Karloff for the original discussion on the disjoint path facility location problem. We also thank the anonymous reviewer for helpful comments on the manuscript.
Author information
Authors and Affiliations
Contributions
All authors contributed to the initial idea of the study. Y.C. and S.J. showed the theoretical results. S.J., D.P. and S.K. designed the numerical tests and analyzed the results. All authors participated in the preparation of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Cao, Y., Jiang, S., Perouli, D. et al. Solving Set Cover with Pairs Problem using Quantum Annealing. Sci Rep 6, 33957 (2016). https://doi.org/10.1038/srep33957
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep33957
This article is cited by
-
Benchmarking Advantage and D-Wave 2000Q quantum annealers with exact cover problems
Quantum Information Processing (2022)
-
Finding Maximum Cliques on the D-Wave Quantum Annealer
Journal of Signal Processing Systems (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


 ,
, 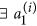 ,
,  such that
such that  and
and  . In other words, ci is covered by the pair
. In other words, ci is covered by the pair  .
.


 index the steps)
index the steps)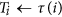 ;
;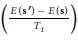 , let
, let  . Otherwise let
. Otherwise let 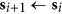 .
.


