Introduction

Entanglement plays a crucial role in quantum information processing1,2,3,4. Some of typical entangled states, such as Bell state5, Greenberger-Horne-Zeilinger (GHZ) state6 and W state7, have attracted great attention in the last decades. However, all of these states are entangled states that are defined in Hilbert spaces with two dimensions. Recently, high-dimensional entanglement has attracted more and more attention due to their superior security than qubit systems, especially in the aspect of quantum key distribution. Besides, it has been demonstrated that violations of local realism by two entangled high-dimensional systems are stronger than that by two-dimensional systems8. Thus, much interest has been focused on the generation of high-dimensional entanglement in theory via various techniques including quantum Zeno dynamics (QZD)9,10,11, stimulated Raman adiabatic passage (STIRAP)12,13 and dissipative dynamics14,15. Also, experimental generations of high-dimensional entanglement have been already achieved16,17.

With no doubt, a lot of remarkable achievements have been made with regard to high-dimensional entangled states. However, most of these high-dimensional entangled states are two-body but few multi-body. For a dozen years, some attention has been paid to multi-body high-dimensional entangled states such as singlet state18 and lots of schemes have been proposed for generations of singlet state19,20,21,22. A short time before, a novel three-body three-dimensional entangled state called tree-type entanglement was prepared via adiabatic passage by Song et al.23. In the ref. 23, the tree-type three-dimensional entanglement was prepared among one single atom and two BECs and the authors predicted that the tree-type three-dimensional entanglement is likely to have great applications in improving quantum communication security.

Among the techniques mentioned above for generations of high-dimensional entanglement, there are two techniques widely used for their robustness against decoherence in certain conditions. One is STIRAP12,13,21,23 and the other is QZD9,10,11,19,20,22. STIRAP is widely used in time-dependent interacting fields and robust against the atomic spontaneous emission and variations in the experimental parameters, but a relatively long interaction time is usually required. QZD is usually robust against photon leakages and does not need a long interaction time. However QZD is sensitive to the atomic spontaneous emissions and variations in the experimental parameters. Thus some of researchers introduce detuning between the atomic transitions to restrain the influence of atomic spontaneous emissions10, but the interaction time significantly increases unavoidably. Therefore, in order to solve the problem of long interaction time, researchers have paid more attention to “shortcut to adiabatic passage” which employs a set of techniques to speed up a slow quantum adiabatic process24,25,26,27,28,29,30,31,32,33,34,35. Further more, the multiple Schrödinger pictures and dynamics are introduced to implement physically feasible transitionless quantum driving (TQD) for two-36,37 and three-level38 quantum systems and it offers an effective way for experimental realizations of robust quantum information processing. Recently, the transitionless superadiabatic protocols were experimentally implemented, which make the system follow the instantaneous adiabatic ground state nearly perfectly39. The nonadiabatic holonomic quantum computation, which possesses the advantage of robustness against decoherence and enjoys a short operation time at the same time, was realized in experiment40. Assisted quantum adiabatic passage was experimentally implemented in a single spin41. Up to the present, Lewis-Riesenfeld invariants (LRI) and TQD for shortcuts to adiabatic passage, were used widely to speed up the operations of multi-particle systems, such as fast multi-particle quantum state transfer42,43, fast generations of entanglement44,45,46 and fast constructions of quantum gates47,48,49,50,51.

In this paper, we propose two schemes for fast generating of tree-type three-dimensional entanglement among three spatially separated atoms via LRI and TQD, respectively. Based on LRI and TQD we construct effective shortcuts to adiabatic passage for fast generating tree-type three-dimensional entanglement among three atoms trapped respectively in three spatially separated cavities connected by two fibers. We will give the interesting comparisons between the LRI method and the TQD method. The generations of tree-type three-dimensional entanglement in our schemes are implemented within a short time and the strict numerical simulations demonstrate that our schemes are both robust against the decoherence caused by the atomic spontaneous emissions, photon leakages and the variations in the parameters.

Preliminary Theory

Lewis-Riesenfeld invariants

Here we give a brief description about Lewis-Riesenfeld invariants theory52. A quantum system is governed by a time-dependent Hamiltonian H(t) and the corresponding time-dependent Hermitian invariant I(t) satisfies

The solution of the time-dependent Schrödinger equation can be expressed by a superposition of invariant I(t) dynamical modes |Φn(t)〉

where Cn is the time-independent amplitude, αn is the time-dependent Lewis-Riesenfeld phase and |Φn(t)〉 is one of the orthogonal eigenvectors of the invariant I(t) satisfying with a real eigenvalue λn. The Lewis-Riesenfeld phases are defined as

Transitionless quantum driving

Suppose a system is dominated by a time-dependent Hamiltonian H0(t) with instantaneous eigenstates |ϕn(t)〉 and eigenvalues En(t),

When a slow change satisfying the adiabatic condition happens, the state of the system governed by H0(t) can be expressed as26,53

Because the instantaneous eigenstate |ϕn(t)〉 do not meet the Schrödinger equation, there may be transitions between the eigenstates of H0(t) with a finite probability during the whole evolution process even under the adiabatic condition. In order to construct the Hamiltonian H(t) that exactly drives the instantaneous eigenstates |ϕn(t)〉s, i.e., there are no transitions between different eigenstates during the whole evolution process, the simplest choice of the Hamiltonian H(t) can be written as

Therefore, as long as H(t) is constructed, the system will evolves with no transitions between different eigenstates.

Quantum Zeno dynamics

Assume that a quantum system’s dynamics evolution is governed by the Hamiltonian

where Hobs can be viewed as the Hamiltonian of the quantum system investigated and Hmeas as an additional interaction Hamiltonian performing the measurement. K is a coupling constant and in the strong coupling limit K → ∞, the whole system is governed by the Hamiltonian54

where Pn is one of the eigenprojections of Hmeas with eigenvalues λn(). Interestingly, it is easy to deduce that the system state will remain in the same Zeno subspace as that of its initial state. In particular, if the system is initially in the dark state |Ψd〉 of Hmeas, i.e., Hmeas|Ψd〉 = 0, the the Hamiltonian (8) reduces to

Description of the physical model

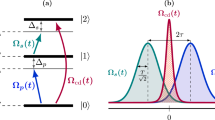
The schematic setup for generating the tree-type three-dimensional entanglement is shown in Fig. 1(a). Three atoms are trapped respectively in three spatially separated optical cavities which are connected by two fibers. Under the short fiber limit (lv)/(2πc) ≤ 1, only the resonant modes of the fibers interact with the cavity modes55, where l is the length of the fiber and v is the decay rate of the cavity field into a continuum of fiber modes. The atomic level configurations and relevant transitions are shown in Fig. 1(b). As shown in Fig. 1(b), the five-level atom1 and atom3 are both M-type with two excited states |eL〉 and |eR〉 and three ground states |gL〉, |g0〉 and |gR〉. The four-level atom2 is tripod-type with one excited state |e0〉 and three ground states |gL〉, |g0〉 and |gR〉. The atomic transition (j = 1, 3) is resonantly coupled to the left-circularly (right-circularly) polarized mode of jth cavity with corresponding coupling constant gj,L(R) and is resonantly coupled to the left-circularly (right-circularly) polarized mode of cavity2 with corresponding coupling constant g2,L(R)). The transitions and are resonantly driven by classical laser fields with the time-dependent Rabi frequencies Ωj(t) and Ω2(t), respectively. Then the whole system can be dominated by the interaction Hamiltonian (ħ = 1):

Figure 1
figure 1

(a) The schematic setup for generating tree-type three-dimensional entanglement; (b) the level configurations and relevant transitions. (c) The APF design of the schematic setup for TQD to fast generate tree-type three-dimensional entanglement.

Full size image

where Htotal is the total Hamiltonian of the whole system, Hal (Hacf) is the interaction between the atoms and the classical laser fields (the cavity-fiber system), v1(2),L(R) is the coupling strength between the modes of the cavity1,2 (cavity2,3) and the modes of the fiber1(2), ak,L(R) (k = 1, 2, 3) is the annihilation operator of left-circularly (right-circularly) polarized mode of kth cavity and is the creation operator of fiber1(2) left-circularly (right-circularly) polarized mode. For simplicity, we assume gk,L(R) and v1(2),L(R) are real, gk,L(R) = g and v1(2),L(R) = v.

Suppose that the total system is initially in the state denoting kth atom in the state |g0〉k and all of three cavities and two fibers in the vacuum state. Thus dominated by the total Hamiltonian in Eq. (10), the whole system evolves in the Hilbert space spanned by

Obviously, the system is initially in the dark state of Hacf, i.e., Hacf|ϕ1〉 = 0. Therefore, under the Zeno limit condition , v(k = 1, 2, 3), the whole system can approximatively evolve in an invariant Zeno subspace consisting of dark states corresponding to the zero eigenvalue of Hacf:

corresponding to the projections

Here,

Therefore, the system Hamiltonian can be rewritten as the following form based on Eq. (9):

Here setting v = g and Ω3(t) = Ω1(t), we can obtain an effective Hamiltonian of the system

in which |Ψ1〉 = |ϕ1〉 and . The instantaneous eigenstates of H0(t) corresponding respectively to the eigenvalues λ0 = 0 and are

where and .

Two methods used to generate tree-type three-dimensional entanglement

The method of Lewis-Riesenfeld invariants

In order to construct a shortcut by the LRI method for fast generating of tree-type three-dimensional entanglement, we are supposed to chase down the Hermitian invariant operator I(t) satisfying . Because of SU(2) dynamical symmetry of H0(t) in Eq. (16), I(t) can be easily given by27,56

where χ is an arbitrary constant in the unit of frequency keeping I(t) in the unit of energy and ν and β are time-dependent auxiliary parameters satisfying the equations

So Ω1(t) and Ω2(t) can be easily deduced as follows:

The solution of Shrödinger equation with respect to the instantaneous eigenstates of I(t) can be written as , where αn(t) is the Lewis-Riesenfeld phase in Eq. (3), and |ϕn(t)〉 is the eigenstate of the invariant I(t) as

Then we consider a series of boundary conditions satisfying and to give

where tf is the operation time. The Eq. (22) is the guarantee for the system to evolve along |n0(t)〉 in Eq. (17) so that we obtain the target state . Therefore, to avoid infinite Rabi frequencies, we can choose the boundary conditions for ν and β as follows:

where ε is a time-independent small value. Then the parameters can be easily set as

and thus we can deduce

Based on the parameters above, we can determine the value of ε by calculating the fidelity

where with the Lewis-Riesenfeld phases

and is the tree-type three-dimensional entanglement generated by the LRI method. Therefore, for the appropriate Rabi frequencies and the fidelity F = 1, we can choose

Thus, the transformation is achieved and we have constructed a shortcut by the LRI method to speed up the generation of the tree-type three-dimensional entanglement.

The method of transitionless quantum driving

Because the instantaneous eigenstates of H0(t) do not meet the Schrödinger equation, there may be transitions between the eigenstates in Eq. (17). Therefore, we need to construct the TQD Hamiltonian H(t) that exactly drives the instantaneous eigenstates with no transitions between different eigenstates. Based on Eq. (6), we learn the simplest Hamiltonian H(t) is derived in the form

Substituting Eq. (17) into Eq. (29), we obtain

in which . The Hamiltonian (30) is constructed by a direct coupling of |Ψ1〉 and |Ψ2〉 and it is too hard to be implemented in experiment for such a complex system we use24,35. However, fortunately inspired by the references44,46, we find an alternative physically feasible (APF) Hamiltonian whose effect is equivalent to H(t). The APF design is shown in Fig. 1(c). Comparing Fig. 1(b,c), we change all of the resonant atomic transitions into non-resonant atomic transitions with detuning Δ.

The interaction Hamiltonian of the non-resonant system reads

Then similar to the approximation for the Hamiltonian from Eqs (10, 11, 12, 13, 14, 15, 16), an effective Hamiltonian for the present non-resonant system can be obtained

Under the limit condition , , by adiabatically eliminating the state |ΨD〉, the effective Hamiltonian becomes

The first two terms can be removed by setting and the final effective Hamiltonian becomes

This effective Hamiltonian is equivalent to the Hamiltonian H(t) in Eq. (30) if we set , i.e.,

which is the correlation between the Rabi frequencies of the TQD method and the Rabi frequencies of STIRAP. By setting the Rabi frequencies of STIRAP to satisfy the same boundary conditions as Eq. (22), we can achieve the transformation to implement the fast generation of tree-type three-dimensional entanglement, where is the tree-type three-dimensional entanglement generated by the TQD method.

Numerical simulations and comparisons between LRI and TQD

In the following, we will give the numerical simulations in three subsections to discuss respectively the selections of parameters of the two methods, the feasibility of generating tree-type three-dimensional entanglement and the robustness of our schemes. Also the comparisons between the LRI method and the TQD method will be included in every subsection.

Selections of parameters

Firstly, to determine the parameters of the LRI method, we plot the fidelity versus the operation time tf and ε in Fig. 2, where |Φ(tf)〉 is the state at the time t = tf of the whole system governed by the total Hamiltonian Htotal in Eq. (10). In Fig. 2(a), we plot the relation between the fidelity and the operation time tf with ε = 0.177 which is determined in Eq. (28). And we can see that in a very short operation time tf = 80/g the fidelity is already almost unity: F(tf = 80/g) = 0.996. From Fig. 2(b), we can find that under tf = 80/g when ε = 0.177 the fidelity is highest. Thus we can choose tf = 80/g and ε = 0.177 as the parameters of the LRI method in the following discussion. Furthermore, in order to consider the joint effects of tf and ε on the fidelity we plot the three dimensional image of the fidelity versus tf/g−1 and ε in Fig. 2(c). From the three dimensional image, it is clear that the effects of tf and ε on the fidelity are not dependent on each other.

Figure 2
figure 2

The fidelity for the LRI method versus (a) tf/g−1 with ε = 0.177 and (b) ε with tf = 80/g, respectively; (c) the three dimensional image of the fidelity for the LRI method versus tf/g−1 and ε.

Full size image

Next we determine the parameters of the TQD method. In order to satisfy the boundary conditions in Eq. (22), the Rabi frequencies Ω1(t) and Ω2(t) in the original Hamiltonian Htotal are chosen as46

where Ω0 is the pulses’ amplitude, tf is the operation time and τ and T are related parameters. The time-dependent Ω1(t) and Ω2(t) are shown in Fig. 3.

Figure 3
figure 3

Time dependence on t/tf of Ω1(t) and Ω2(t) with the parameters τ = 0.14tf, T = 0.19tf.

Full size image

Based on the correlation in Eq. (35), the Rabi frequencies of the TQD method can be figured out. As an illustration, we plot the fidelity versus the detuning Δ and tf in Fig. 4, where |Φ(tf)〉 is the state at the time t = tf of the whole system governed by the total Hamiltonian in Eq. (31). To compare with each other effectively, we choose the same operation time tf = 80/g in the TQD method as that in the LRI method. From Fig. 4(a), we can find that under tf = 80/g when Δ = 6 g the fidelity is highest. Besides, we can see that the fidelity is almost unity: F(tf = 80/g) = 0.996 at the point tf = 80/g from Fig. 4(b). Thus we choose tf = 80/g and Δ = 6 g as the parameters of the TQD method in the following discussion. Similar to the LRI method, in order to consider the joint effects of tf and Δ on the fidelity we plot the three dimensional image of the fidelity versus tf/g−1 and Δ/g in Fig. 4(c). However, from Fig. 4(c), we are not able to judge whether the effects of tf and Δ on the fidelity are dependent or not dependent on each other. We will make a detailed discussion about the joint effects of tf and Δ on the fidelity later in the last subsection.

Figure 4
figure 4

The fidelity for the TQD method versus (a) Δ/g with tf = 80/g and (b) tf/g−1 with Δ = 6 g, respectively; (c) the three dimensional image of the fidelity for the TQD method versus Δ/g and tf/g−1.

Full size image

Next, a brief discussion is very necessary to show our schemes are fast. Firstly, it is quite apparent that the operation time tf = 80/g is far shorter than t = 3000/g which is the generation time of the tree-type three-dimensional entanglement generated in the ref. 23. Further more, for a more effective discussion, we consider the adiabatic condition 57, where is the minimum separation between the eigenvalues of the Hamiltonian (16). For convenience, we just consider the LRI method for the shortcut to adiabatic passage. With a simple calculation, for the shortcut to adiabatic passage, we can obtain the constants and ΔELRI = 0.077 by using Eq. (25). However, for ref. 23, we obtain time-dependent but single-peak and ΔE and the amplitudes are and ΔEmax = 0.067, respectively. Obviously, according to the information above, the adiabatic condition is met in the ref. 23 but needs not to be met in our schemes, which means that the slow process of the generation of the tree-type three-dimensional entanglement is sped up.

Discussion of feasibility

In this subsection, we will give the numerical simulations for discussing the feasibility of our two schemes. For the LRI method, we plot the time-dependent Rabi frequencies Ω1(t) and Ω2(t) which are described by Eq. (25) in Fig. 5(a). The evolutions of populations of states |ϕ1(17~20)〉 governed by Htotal are shown in Fig. 5(b). For the TQD method, we plot the time-dependent Rabi frequency which is described by Eq. (35) in Fig. 5(c). The evolutions of populations of states |ϕ1(17~20)〉 governed by are shown in Fig. 5(d). In addition, in Fig. 6(a) we plot the atomic excited populations (red solid line) and (blue solid line) corresponding to the LRI method and the TQD method respectively and the cavity-fiber excited populations (red dashed line) and (blue dashed line) corresponding to the cases of the LRI method and the TQD method respectively. In Fig. 6(b), we plot the fidelities of the tree-type three-dimensional entanglement generated by the LRI method (red dashed line) and the TQD method (blue solid line), respectively.

Figure 5
figure 5

For the LRI method, (a) the time dependence of the Rabi frequencies Ω1(t) (blue solid line) and Ω2(t) (red dashed line); (b) the populations of states |ϕ1〉 and |ϕ17~20〉 governed by Htotal. For the TQD method, (c) the time dependence of the Rabi frequency ; (d) the populations of states |ϕ1〉 and |ϕ17~20〉 governed by . The parameters used here are tf = 80/g, ε = 0.177, Δ = 6 g, τ = 0.14tf and T = 0.19tf.

Full size image
Figure 6
figure 6

(a) The time dependence of atomic excited populations (red solid line) and cavity-fiber excited populations (red dashed line) in the LRI method and the time dependence of atomic excited populations (blue solid line) and cavity-fiber excited populations (blue dashed line) in the TQD method; (b) the fidelities of tree-type three-dimensional entanglement for the LRI method (red dashed line) and the TQD method (blue solid line). The parameters used here are same as in Fig. 5.

Full size image

Here we first consider Fig. 6(b). From Fig. 6(b), we know that both of the two lines of fidelity illustrated based on the two methods reach a very high point close to unity at the time t = 80/g and thus both of our schemes are feasible. Figure 6(b) also shows that the fidelity of the TQD method can reach a very high value within a shorter time than that of the LRI method. Next we consider the populations of the target states in Fig. 5(b,d). We can see that a near perfect result we expect is obtained in Fig. 5(b), but a little bit imperfect result appears in Fig. 5(d) in which there exists a small gap between two lines of the populations of |ϕ1〉 and |ϕ17~20〉. Therefore, for the transformation of populations, the LRI method is a bit better than the TQD method. However, when compare the pulse types in Fig. 5(a,c), we find that the TQD method is more feasible than the LRI method. Because the pulses in LRI method are short-time truncations of two harmonic pulses and the truncations of the two harmonic pulses in a short time are too hard to be achieved. But the pulses in TQD method are almost complete Gaussian pulses which are relatively easy to be achieved. Moreover, the populations of atomic and cavity-fiber excited states for two methods are shown in Fig. 6(a) and all of the populations of excited states are near zero at the time t = 80/g. So we can deduce that whichever method is employed, the state of the whole system almost populates in tree-type three-dimensional entanglement.

It is worth explaining the gap between the two lines of the populations of |ϕ1〉 and |ϕ17~20〉 in Fig. 5(d). For the TQD method, there are two limit conditions , v(k = 1, 2, 3) and , v applied to prepare tree-type three-dimensional entanglement. However, as shown in Fig. 5(c), the amplitude of is 0.8 g which does not strictly meet the limit condition , v. And also the detuning Δ = 6 g does not strictly meet the limit condition , v. In fact, these two limit conditions are difficult to be coordinated. With no assignments of tf and Δ, we calculate the amplitude of with the parameters τ = 0.14tf and T = 0.19tf to obtain

which is not dependent on the amplitude Ω0 of Ω1,2(t) in Eq. (36) but only proportional to . Thus, roughly equals to /3 if the operation time is chosen as tf = 80/g. Nevertheless, the ratio 1/3 is not small enough to satisfy both two limit conditions , v and , v, i.e., the condition , v will not be satisfied if the limit condition , v is satisfied and vice versa. Therefore, there exists a gap between the two lines of the populations of |ϕ1〉 and |ϕ17~20〉 in Fig. 5(d). In addition, Eq. (37) reveals that ’s amplitude . It is known that the fidelity of the TQD method is strongly dependent on , so we can deduce that the fidelity of the TQD method is strongly dependent on the value of Δ/tf. As a result, in Fig. 4(c), the effects of tf and Δ on the fidelity are dependent on each other.

Based on the discussion above, for fast generating tree-type three-dimensional entanglement, both the LRI method and the TQD method are feasible. Besides, the two methods have their own advantages and disadvantages and we can choose a certain method depending on the conditions in experiment.

Discussion of robustness

In the above discussion, the whole system are perfect and considered as absolutely isolated from the environment. Therefore, it is necessary to give the discussions of robustness of our schemes against the variations in the parameters and decoherence induced by the atomic spontaneous emissions and photon leakages of the cavity-fiber system. For discussing the effects of the variations in the parameters, we plot the fidelity of the LRI method versus the variations in tf and ε in Fig. 7(a) and the fidelity of the TQD method versus the variations in tf and Δ in Fig. 7(b). Here we define δx = x′ − x as the deviation of x, in which x denotes the ideal value and x′ denotes the actual value. In Fig. 7(a), the fidelity decreases with the increase of |δε| as described in Fig. 2(b). From Eq. (25), we know that the Rabi frequencies decrease with the increase of the operation time tf. According to the limit condition , v we use, the values of the Rabi frequencies are the smaller the better, so the operation time tf is the longer the better as described in Fig. 2(a). Therefore, the fidelity of the LRI method increases with the increase of δtf in Fig. 7(a). In Fig. 7(b), we can clearly see that the effects of tf and Δ on the fidelity of the TQD method are dependent on each other and even the fidelity of the TQD method is apparently dependent on the value of Δ/tf as mentioned in the last subsection. Significantly, we notice that the fidelities of the two methods are both over 0.98 even when . Therefore, both of our schemes are robust against the variations in the parameters.

Figure 7
figure 7

(a) The fidelity of the LRI method versus δtf/tf and δε/ε; (b) the fidelity of the TQD method versus δtf/tf and δΔ/Δ. The parameters used here are same as in Fig. 5.

Full size image

We can also see that the smallest fidelity of the TQD method in Fig. 7(b) is slightly higher than the smallest fidelity of the LRI method in Fig. 7(a). This fact can easily be found by comparing Figs 2(c) and 4(c), in which there is a greater advisable range of the parameters in the TQD method than in the LRI method for preparing tree-type three-dimensional entanglement with a high fidelity.

Next taking the decoherence induced by the atomic spontaneous emissions and photon leakages of the cavity-fiber system into account, the whole system is dominated by the master equation

where H is the total Hamiltonian Htotal of the LRI method in Eq. (10) or of the TQD method in Eq. (31). is the spontaneous emission rate of jth atom from the excited state |ei〉j to the ground state |gi〉j; and denote the photon leakage rates from the fiber modes and the cavity modes, respectively; (m, n = ei, gi) is Pauli operators. For simplicity, we assume and .

Based on the master equation, we plot the fidelities of the LRI method and the TQD method versus and γ/g in Fig. 8. As we can see from the decrease of the fidelity of the LRI method with the increases of and γ/g in Fig. 8(a), we learn that the influence of atomic spontaneous emissions on the fidelity is greater than that of photon leakages of the cavity-fiber system. However, in Fig. 8(a) the influence of cavity-fiber photon leakages on the fidelity of the TQD method plays a full role, but that of atomic spontaneous emissions is little. As a cross reference, we can get some inspiration from Fig. 6(a). In Fig. 6(a), the highest value of the cavity-fiber excited populations (blue dashed line) of the TQD method is over 0.2 during the evolution process but that of the atomic excited populations (blue solid line) of the TQD method is near zero which caused by the detuning Δ. The highest values of the atomic excited populations (red solid line) and the cavity-fiber excited populations (red dashed line) of the LRI method are slightly higher and slightly lower than 0.05, respectively. Therefore, it is no doubt that the results of Figs 6 and 8 are corresponding to each other. Finally, it is necessary to emphasize that the fidelities of the LRI method and the TQD method are near 0.94 and over 0.955 respectively, even when . Therefore, our two schemes of the LRI method and the TQD method both are robust against the decoherence induced by the atomic spontaneous emissions and photon leakages of the cavity-fiber system.

Figure 8
figure 8

The fidelity of (a) the LRI method and (b) the TQD method for generating tree-type three-dimensional entanglement versus κ/g and γ/g, respectively. The parameters used here are same as in Fig. 5.

Full size image

Experimental feasibility and conclusion

Now we show the experimental feasibility of our schemes. As mentioned in the ref. 23, 87Rb can be used in our schemes to construct the required atomic level configurations. For 87Rb, , and of 5S1/2 can be used as the ground states |gL〉, |g0〉 and |gR〉 respectively and , and of 5P3/2 can be used as the excited states |eL〉, |e0〉 and |eR〉 respectively. Based on a set of cavity QED parameters g = 2π × 750 MHz, γ = 2π × 3.5 MHz and κ = 2π × 2.62 MHz, which are achieved in recent experiments58,59,60, we can obtain the very high fidelities FLRI = 0.984 and FTQD = 0.990 corresponding to the LRI method and the TQD method respectively, which show our schemes for generating tree-type three-dimensional entangled states both are feasible in the experiment.

In conclusion, we have proposed two schemes to speed up the generations of the tree-type three-dimensional entanglement via Lewis-Riesenfeld invariants and transitionless quantum driving. The two different tree-type three-dimensional entangled states are prepared among three atoms trapped respectively in three spatially separated optical cavities connected by two fibers. The strict numerical simulations show that the LRI method and the TQD method both are feasible and robust against the variations in the parameters, atomic spontaneous emissions and photon leakages of the cavity-fiber system. Besides, comparing the two methods, we know they both have their own advantages and disadvantages. So we can choose different methods depending on different conditions in experiment. In short, both of our schemes are fast, robust and feasible. We hope that the tree-type three-dimensional entanglement would contribute to the improvement of quantum communication security and our work would be useful for the experimental realization of quantum information processing in the near future.

Additional Information

How to cite this article: Wu, J.-L. et al. Fast generations of tree-type three-dimensional entanglement via Lewis-Riesenfeld invariants and transitionless quantum driving. Sci. Rep. 6, 33669; doi: 10.1038/srep33669 (2016).