Abstract
In an electronic device based on two dimensional (2D) transitional metal dichalcogenides (TMDs), finding a low resistance metal contact is critical in order to achieve the desired performance. However, due to the unusual Fermi level pinning in metal/2D TMD interface, the performance is limited. Here, we investigate the electronic properties of TMDs and transition metal oxide (TMO) interfaces (MoS2/MoO3) using density functional theory (DFT). Our results demonstrate that, due to the large work function of MoO3 and the relative band alignment with MoS2, together with small energy gap, the MoS2/MoO3 interface is a good candidate for a tunnel field effect (TFET)-type device. Moreover, if the interface is not stoichiometric because of the presence of oxygen vacancies in MoO3, the heterostructure is more suitable for p-type (hole) contacts, exhibiting an Ohmic electrical behavior as experimentally demonstrated for different TMO/TMD interfaces. Our results reveal that the defect state induced by an oxygen vacancy in the MoO3 aligns with the valance band of MoS2, showing an insignificant impact on the band gap of the TMD. This result highlights the role of oxygen vacancies in oxides on facilitating appropriate contacts at the MoS2 and MoOx (x < 3) interface, which consistently explains the available experimental observations.
Similar content being viewed by others
Introduction
The aggressive miniaturization of silicon-based electronics, reaching a fundamental limit of scaling, has motivated the electronic device community to explore for alternative channel materials and device architectures for the future transistor technology1,2. Within this context, atomically thin two dimensional (2D) graphene and hexagonal boron nitride (h-BN) have emerged as potential candidates for device application because of the advances in exfoliation methods and synthetic techniques3,4,5,6. However, due to the lack of a sizeable band gap in graphene and the large band gap (>5 eV) of h-BN, these 2D materials have limitations in their use as channel materials in low power transistor applications. In the search for other thin 2D semiconductors with optimum electronic properties, 2D transition metal dichalcogenides (TMDs) have recently attracted a significant interest, as these materials possess sizeable band gaps (1–2 eV), ideally no dangling bonds and correspondingly low trap densities at semiconductor-dielectric interface allowing efficient electrostatics, as well as the reduction of short channel effects7,8. Moreover, TMDs provide a wide range of materials choices, and have tunable electronic and optical properties through thickness control, mixed alloys9,10, combination of TMD heterostructures, phase and strain engineering or with the application of an external electric or magnetic field11,12,13. Additionally, the electronic and optical properties can be modulated through the dielectric environment14,15,16. Single layer TMDs have a direct type band gap in the visible portion of the electromagnetic spectrum. As a result, TMDs are especially suitable for optoelectronic, digital electronics, and display devices.
However, there are still various challenges before the realization of an ideal device concept based on TMDs. Perhaps the most important is to find a suitable contact between a true metal and the TMD semiconductor with low interfacial resistance, to enable efficient charge injection and/or extraction. Thus, achieving low contact resistance for TMD-based nano-electronic devices is the critical first step in order to get a good device performance. There are reports on true metal contacts with TMDs showing several problems, including degradation of the performance of TMD transistors due to undesired interface reactions, contact resistance or posing an abnormal Fermi level pinning at the band gap of the semiconductor17,18,19. Moreover, recent studies have shown the importance of the contact metal deposition ambient and the resultant contact properties20,21,22. Therefore, alternative contact materials which can effectively facilitate the charge transfer between the source/drain and the semiconductor (channel material) need to be sought. There has also been research on stable doping strategies to lower the contact resistance23,24, and different options, like transition metal oxides, have been used as a barrier layer between metals and organic semiconductors in organic photovoltaics (OPVs) devices for selective charge transfer25. However, utilizing a metal oxide contact layer with transition metal dichalcogenides has not been realized until recently26,27,28. Hence, the specific nature of their interfacial electronic properties must be accurately determined before pursuing further extensive research on TMDs-metal oxide contacts.
Another interesting possibility is given by the corresponding TMD-TMO interfaces. From this point of view, Molybdenum trioxide (MoO3) could be considered as a promising hole contact on MoS2-based Field Effect Transistors (FET). MoO3 is stable in ambient conditions, and it provides an efficient hole extraction. Unlike true metal contacts, it does not induce Fermi level pinning at the interface. Our own work has previously shown that the interaction with metals at metal-TMD interface modifies the transition metal-chalcogen hybridization of the TMD, inducing states in the band gap, which ultimately results in unusual Fermi level pinning17. Accordingly, there is an urgent need to find a suitable contact material or barrier layer that could also avoid Fermi level pinning, resulting in a nearly Ohmic contact. Currently, TMD-based devices are measured with Schottky limited electrical characteristics23. A good contact would facilitate the electron injection and extraction during the device operation.
In this paper, we present an investigation on the atomic structures and electronic properties of MoS2/MoOx (x ≤ 3) interfaces for future FET-based device applications26,27,28. Our results show that TMD and MoOx interfaces enable ideal p-type contact characteristics for future transistor technology. Moreover, due to defect-induced gap states (i.e., defect bands) in sub-stoichiometric MoOx, the interface presents an Ohmic character, which may result in a promising Ohmic contact for TMD-based electronic devices. Therefore, this work provides a fundamental understanding of the interfacial electronic properties of MoS2 and both pristine and oxygen deficient MoOx (x ≤ 3).
Methodology
First-principles calculations based on Density Functional Theory (DFT)28,29,30,31 with plane wave basis set and Projector Augmented Wave (PAW)32,33 pseudopotentials have been performed using the Vienna Ab-initio Simulation Package (VASP)33,34,35. The electronic wave functions were represented by plane wave basis with a cutoff energy of 500 eV and the exchange correlation interactions were incorporated as a functional of the Generalized Gradient Approximation (GGA)34. Additional calculations included the hybrid Heydt-Scuseria-Ernzerhof (HSE) exchange- correlation functional36 and many body methods (GW0)37. In order to investigate the MoS2/MoO3 contact interface, a supercell structure with a S-terminated MoS2 (001) surface and a O-terminated MoO3 (010) surface was constructed. The lattice mismatch for such superstructure is less than 1% (the strain is on the MoO3 surface). Periodically repeated slabs separated by a 16 Å thick vacuum region were used, in order to avoid the interaction between the two surfaces of the slab as a result of the periodic boundary conditions (PBC). During the calculations, the atoms were allowed to relax while the cell size was kept fixed. A Г-centered 6 × 6 × 1 and a 12 × 12 × 1 k-point meshes were then used for the self-consistent field (SCF) and density of states (DOS) calculations, respectively. The energy and forces were converged until a tolerance value of 10−5 eV and 0.01 eV/Å, respectively. Because standard DFT is unable to grasp the physics of van der Waals (vdW) interactions leading to overestimating the interlayer separation in layered materials, the Grimme vdW-D2 approach38,39 was adopted in order to optimize the MoS2 and MoO3 interlayer distance accurately.
Results and Discussion
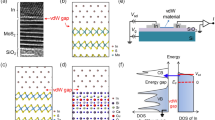
We first investigate the electronic properties of bulk and single layer Molybdenum-trioxide (MoO3) in detail. MoO3 shows two phases (α and β): α-MoO3 is stable in an orthorhombic crystal structure with space group Qh26 (Pbnm) (the unit cell lattice parameters are a = 3.962 Å, b = 13.855 Å, and c = 3.699 Å), and the β phase is observed only at high pressure and is metastable at ambient conditions40,41. In the α-MoO3 phase (the one considered in this work), each unit cell contains four MoO3 formula units and has an easy cleavage (010) plane, as shown in Fig. 1(a,b). Each monolayer consists of two sublayers, with periodically arranged MoO6 octahedra. Thus, the crystal structure contains three distinct oxygen atoms due to their different coordination: asymmetrical bridging oxygen (unequal bond length with Mo), symmetric bridging oxygen (two Mo bonds with the same bond length and an elongated bond to the next sublayer), and terminal oxygen (single bond Mo-O). The terminal oxygen atom is preferentially deficient during an exfoliation process. The interlayer metal to metal distance d (Mo-Mo) is ~7.00 Å (the Mo-Mo distance within the same layer is 4.03 Å), and the effective vdW gap, d (O-O), is ~0.799 Å (See Fig. 1(a)). The electronic band structure for bulk MoO3 is shown in Fig. 1(c), which indicates that the band gap is of indirect type with the valance band maximum (VBM) at U (0.5 0.0 0.5) and the conduction band minimum (CBM) at Г (0.0 0.0 0.0) point. Our obtained band gaps (Eg) are 1.9 and 2.7 eV at the GGA and HSE levels of calculation, respectively. The HSE result is closer to the experimental values of 3.2 eV for bulk and 2.8 eV for polycrystalline MoO3, as obtained from absorption spectra measurements40. As can be seen in the DOS shown in Fig. 2(a), the MoO3 CBM is mainly contributed by Mo d states and the VBM by O p states.
(a) Side view of the atomic structure of the MoO3 unit cell. The interlayer metal to metal distance and the vdW gap are indicated by d(Mo-Mo) and d(O-O), respectively. (b) The MoO3 4 × 1 × 4 supercell used for the defects study, showing the layered structure along the [010] direction. Red and purple spheres represent O and Mo atoms, respectively. (c) Electronic band structure of bulk MoO3, showing the indirect band gap (indicated by an arrow) with the CBM at Г (0.0 0.0 0.0) and the VBM at U (0.5 0.0 0.5) high-symmetry k-points.
DOS for bulk MoO3 in (a) pristine form, (b) with Mo vacancy (VMo), and (c) O vacancy (VO). Red, and black lines represent O and Mo DOS, respectively. Gap states caused by defects are indicated by arrows. (d) The electrostatic potential variation along the [010] direction is shown for a single MoO3 layer. The inset shows the atomic and electronic band structures for monolayer.
Oxygen vacancies can be easily created by ion bombardment or loss of preferential bridging oxygens from reactions and/or annealing. Such oxygen vacancies may cause surface reconstruction depending on their concentration, by turning exposed Mo atoms into chemically active sites and participating in the adsorption of new species or MoOx reconstruction. MoOx has a very large work function (~6.67 eV from our DFT calculations, close to available experimental values26,42), compared to the work function of metals43 For defective, MoOx, we have computed the formation energy (Eform = Edefect − Eperfect + μx, where, μ: chemical potential of x = Mo and O) of Mo and O vacancies. Our results show that the O vacancy (VO) is energetically more favorable (by ~2 eV) than the Mo vacancy (VMo). Figure 2(b,c) show the corresponding DOS. Both defects induce gap states in the MoO3-x band gap. However, the Mo vacancy induces multiple gap states (of O p nature) close to the VBM (see Fig. 2(b)) due to unsaturated oxygen atoms, whereas an O vacancy leaves a Mo dangling bond, causing defect states of Mo d nature close (0.56 eV) to the CBM, as shown in Fig. 2(c). The defect level shifts downwards by 0.29 eV when using HSE. However, its electronic nature is not modified (i.e., its relative position in the band gap is not changed).
Similar to MoS2, MoO3 shows strong intralayer chemical bonds (Mo-O) and a relatively weak van der Waals interlayer interaction, which facilitates the exfoliation. Since MoO3 layers are stacked along the [010] direction, they can be easily cleaved and exfoliated to produce a thin quasi-2D crystal. The exfoliated monolayer of MoO3 contains two layers of Mo atoms with a thickness of ~1.38 nm (the lattice parameters of the single layer unit cell are a = 0.39 nm, b = 0.613 nm, c = 0.36 nm). From bulk to monolayer MoO3, the change in the electronic properties is not as significant as in the case of MoS2. Figure 2(d: inset) shows the electronic band structure of monolayer MoO3 (010). The obtained band gaps are Eg = 1.804 eV (GGA), Eg = 2.097 eV (GGA + U), Eg = 2.86 eV (HSE) and Eg = 3.66 eV (GW0). The gap is always indirect irrespective of the thickness, unlike MoS2 which shows a direct-indirect transition with decreasing thickness. The conduction band edge is dominated by Mo d orbitals and the valance band edge is mainly contributed from O 2p states, as in the bulk case. The work function (ɸ = Evac − EF; where Evac is the vacuum level and EF the Fermi level) is also estimated to be ~6.6 eV from our DFT calculations, close to the experimental value26,42.
In order to investigate the electronic properties of the MoS2/MoO3 interface, a heterostructure using the MoO3 (010) and MoS2 (001) monolayer surfaces was constructed and subsequently optimized. If any defects are present, the electronic properties of the pristine MoS2 (001) monolayer will be altered significantly and a surface passivation treatment will be crucial before constructing the interface44,45,46. Figure 3(a) shows the atomic configuration of the MoS2/MoO3 interface model. As stated previously, the corresponding interlayer distance optimization was done using the DFT + vdW approach, to account for the weak MoS2-MoO3 interaction. Our calculations show that standard DFT overestimates the interlayer distance by ∆d ~1.7 Å, with the obtained DFT + vdW result being d(S-O) ~2.8 Å. The DOS of the optimized interface model reveals the relative band alignments between both monolayers. The overall band gap of the pristine MoS2/MoO3 stack is substantially reduced (~0.22 eV) with respect to the respective separate counterparts, due to the metal oxide empty states appearing in the band gap energy range of MoS2. Including the HSE correction, the interface band gap only increases to 0.51 eV, even though the gaps of the individual monolayers widen significantly. As shown in Fig. 3(b), the VBM of MoS2 is located close to the CBM of MoO3.
(a) Atomic structure of the stoichiometric MoS2/MoO3 interface. Red, purple and yellow spheres represent O, Mo and S atoms, respectively. The interlayer distance was optimized using the DFT + vdW approach. (b) The corresponding DOS of the interface. Green and blue lines represent the DOS of S and Mo atoms from the MoS2 layer, whereas red and pink lines correspond to the O and Mo atoms from the MoO3 layer.
Then, the conduction bands of MoO3 are lowered relative to those of MoS2, thus making a negative conduction band offset (CBO); this will result in the population of the upper MoO3 energy level from the MoS2 Fermi level. Mo d orbitals hybridized with O p orbitals from the MoO3 layer dominate the CBM, with MoS2 Mo d and S p hybridized orbitals dominating the VBM. The relatively small band gap makes this junction a promising contact heterostructure for tunnel field effect devices, where the gap, the band alignment and the interband charge carrier tunneling can be further controlled by an external applied field and the gate bias.
MoO3 is thought to contain a certain amount of oxygen vacancies (up to 3%), and is known to behave as a p-type contact with TMDs or other semiconductors26. Therefore, a model interface structure with oxygen vacancies was also investigated, in order to examine the effect of possible O vacancies on the electronic properties. Indeed, our calculations show that the MoOx interfacial layer can behave as a p-type contact. Moreover, a unique band alignment between (MoS2/MoOx) with an almost zero charge injection barrier is formed, as demonstrated by the DOS shown in Fig. 4(b). The MoS2/MoOx contact does not cause Fermi level pinning, showing a superior contact performance over other true metals17,18,19. Therefore, our results clarify why the defective MoS2/MoOx interface can also be used as an ideal hole contact for TMD-based devices, besides the well-studied organic semiconductors. The presence of O vacancies produce Mo dangling bonds, which induces defect gap states in the upper region of the MoOx band gap (close to the CBM). Moreover, this is an extraordinarily localized effect with only slight changes showed in the electronic structure of the neighboring atoms. These defect states of Mo 4d nature are just empty states that can be easily filled by electron transfer from the valance band of the MoS2 layer, creating the p-type MoS2. In other words, it behaves as a MoOx hole contact layer, injecting holes into the MoS2.
(a) Side view of the atomic structure of a non-stoichiometric MoS2/MoOx interface model. The oxygen vacancy site is indicated by an arrow pointing to a circle. Red, purple and yellow spheres represent O, Mo and S atoms, respectively. (b) The corresponding DOS of the defective interface. The green and blue filled lines represent the DOS of S and Mo atoms from the MoS2 layer, whereas red and pink filled lines corresponds to the O and Mo atoms from the MoOx layer. The arrow indicates the gap states caused by an oxygen vacancy in the MoO3 layer.
Therefore, MoOx has a great potential to be used as an efficient hole injection layer by charge transport through the valence band, thus making a TMD-based p-FET. The overall performance of a hypothetical FET electronic device depends on the metal/MoOx and MoOx/TMD contacts. However, the metal/MoOx contact resistance can be properly tuned with a suitable choice of metal with a specific work function43. On the contrary, MoOx/MoS2 contacts have been regarded as a major hurdle for many years. Recent experimental reports have shown a low hole Schottky barrier in a device study utilizing MoOx contacts with MoS2 and WSe2 TMDs26.
Due to the relatively large difference between the VBM and the CBM of the MoOx, the band alignment with MoS2 should also be very suitable for tunneling device applications. MoOx films were also found to be oxygen-deficient in a nitrogen environment, enhancing the device performance by means of a gap state mechanism47 which is consistent with the results of this work. Furthermore, by changing the thickness of MoOx and MoS2 layers, additional broad gap states can be introduced, which would substantially increase the hole transport48.
The interfacial electronic transport can also be modulated with an applied external electric field. However, synthesizing ideal or completely stoichiometric MoO3, or having controlled oxygen vacancy formation is actually a challenge. Thus, the contact is better realized due to the presence of oxygen vacancies in the MoO3. Interestingly, the formation of self-limiting WOx (x < 3) on atomically thin WSe2 was used as charge transfer dopants and low hole Schottky barrier contacts for p-WSe2 transistors49. Hence, given the numerous possible transition metal oxides with a wide range of work functions and electronic structures, and the additional available options to tailor their properties, such as modifying the defect concentration or the cation oxidation states, this research focused on hole contacts based on metal oxides-TMD heterostructures, and opens a new avenue to explore 2D TMDs and TMO interfaces for optimization of the device functionality.
Summary
The electronic properties of the sub-stoichiometric MoOx/MoS2 interface have been investigated using DFT calculations. Our results reveal that, due to the large work function of MoO3, a unique and useful band alignment between MoS2 and MoO3 is observed, which can open a potential application in FET. Moreover, our findings are in excellent agreement with experimentally-observed sub-stoichiometric MoOx that shows a defect level alignment with the valance band of the TMD, creating an Ohmic-type contact perfectly suitable for metal-semiconductor device contact purposes. This result also indicates that the MoOx/MoS2 interface facilitates spontaneous charge transfer from the TMD to MoOx and vice versa. In other words, the defect state in the band gap of MoOx assists the hole injection at the interface (through the formation of a low hole injection barrier, thus facilitating an Ohmic injection). This theoretical work sheds light on the atomic level mechanisms of TMD/TMO interfaces, showing their promising characteristics for semiconductor device applications.
Additional Information
How to cite this article: KC, Santosh et al. Electronic properties of MoS2/MoOx interfaces: Implications in Tunnel Field Effect Transistors and Hole Contacts. Sci. Rep. 6, 33562; doi: 10.1038/srep33562 (2016).
References
del Alamo, J. A. Nanometre-scale electronics with III–V compound semiconductors. Nature 479(7373), 317–323 (2011).
International Technology Roadmap for Semiconductors (ITRS). http://www.itrs.net/ (2013).
Novoselov, K. S. et al. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 102(30), 10451–10453 (2005).
Novoselov, K. S. et al. A. Electric Field Effect in Atomically Thin Carbon Films. Science 306(5696), 666–669 (2004).
Geim, A. K. & Novoselov, K. S. The rise of graphene. Nat Mater 6(3), 183–191 (2007).
Lee, G.-H. et al. J. Electron tunneling through atomically flat and ultrathin hexagonal boron nitride. Appl. Phys. Lett. 99(24), 243114 (2011).
Radisavljevic, B., Radenovic, A., Brivio, J., Giacometti, V. & Kis A. Single-layer MoS2 transistors. Nat Nanotechnol 6(3), 147–150 (2011).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 105(13), 136805 (2010).
Zhang, C. et al. Charge Mediated Reversible Metal-Insulator Transition in Monolayer MoTe2 and WxMo1-xTe2 Alloy. ACS nano, doi: 10.1021/acsnano.6b00148 (2016).
KC, S., Zhang, C., Hong, S., Wallace, R. M. & Cho, K. Phase stability of transition metal dichalcogenide by competing ligand field stabilization and charge density wave. 2D Mater. 2(3), p.035019 (2015).
Fang, H. et al. A. High-Performance Single Layered WSe2 p-FETs with Chemically Doped Contacts. Nano Lett. 12(7), 3788–3792 (2012).
Liu, H., Neal, A. T. & Ye, P. D. Channel Length Scaling of MoS2 MOSFETs. ACS Nano 6(10), 8563–8569 (2012).
Yoon, Y., Ganapathi, K. & Salahuddin, S. How Good Can Monolayer MoS2 Transistors Be? Nano Lett. 11(9), 3768–3773 (2011).
Ryou, J., Kim, Y. S., KC, S. & Cho, K. Monolayer MoS2 Bandgap Modulation by Dielectric Environments and Tunable Bandgap Transistors. Sci Rep. 6 (2016).
Chernikov, A. et al. Exciton binding energy and nonhydrogenic Rydberg series in monolayer WS2 . Phys. Rev. Lett. 113(7), p.076802 (2014).
Komsa, H. P. & Krasheninnikov, A. V. Effects of confinement and environment on the electronic structure and exciton binding energy of MoS2 from first principles. Phys. Rev. B. 86(24), p.241201 (2012).
Gong, C., Colombo, L., Wallace, R. M. & Cho, K. The Unusual Mechanism of Partial Fermi Level Pinning at Metal–MoS2 Interfaces. Nano Lett. 14(4), 1714–1720 (2014).
Santos, E. J. G. & Kaxiras, E. Electrically Driven Tuning of the Dielectric Constant in MoS2 Layers. ACS Nano 7(12), 10741–10746 (2013).
Kang, J., Liu, W., Sarkar, D., Jena, D. & Banerjee, K. Computational Study of Metal Contacts to Monolayer Transition-Metal Dichalcogenide Semiconductors. Phys. Rev. X 4(3), 031005 (2014).
Smyth, C. M., Addou, R., McDonnell, S., Hinkle, C. L. & Wallace, R. M. Contact Metal-MoS2 Interfacial Reactions and Potential Implications on MoS2-Based Device Performance. J. Phys. Chem. C 120(27), pp 14719–14729 (2016).
McDonnell, S., Smyth, C., Hinkle, C. L. & Wallace, R. M. MoS2–Titanium Contact Interface Reactions. ACS Appl. Mater. Interfaces, 8(12), pp. 8289–8294 (2016).
English, C. D., Shine, G., Dorgan, V. E., Saraswat, K. C. & Pop, E. Improved Contacts to MoS2 Transistors by Ultra-High Vacuum Metal Deposition. Nano lett. 16(6), pp 3824–3830 (2016).
Du, Y., Yang, L., Liu, H. & Ye, P. D. Contact research strategy for emerging molybdenum disulfide and other two-dimensional field-effect transistors. APL Mater. 2(9), 092510 (2014).
Zhao, P. et al. Air Stable p-Doping of WSe2 by Covalent Functionalization. ACS Nano 8(10), 10808–10814 (2014).
Kröger, M. et al. A. Role of the deep-lying electronic states of MoO3 in the enhancement of hole-injection in organic thin films. Appl. Phys. Lett. 95(12), 123301 (2009).
Chuang, S. et al. MoS2 P-type Transistors and Diodes Enabled by High Work Function MoOx Contacts. Nano Lett. 14(3), 1337–1342 (2014).
Battaglia, C. et al. Silicon heterojunction solar cell with passivated hole selective MoOx contact. Appl. Phys. Lett. 104(11), 113902 (2014).
McDonnell, S. et al. Hole Contacts on Transition Metal Dichalcogenides: Interface Chemistry and Band Alignments. ACS Nano, 8(6), 6265–6272 (2014).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Compu. Mater. Sci. 6(1), 15–50 (1996).
Parr, R. G. Density-Functional Theory of Atoms and Molecules. (Oxford University Press, USA, 1989).
Kohn, W. & Sham, L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 140(4A), A1133–A1138 (1965).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59(3), 1758–1775 (1999).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50(24), 17953–17979 (1994).
Kresse, G. & Hafner, J. Ab-initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 49(20), 14251–14269 (1994).
Perdew, J. P. & Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 23(10), 5048–5079 (1981).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118(18), 8207–8215 (2003).
Hedin, L. New Method for Calculating the One-Particle Green’s Function with Application to the Electron-Gas Problem. Phys. Rev. 139(3A), A796–A823 (1965).
Grimme, S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Compu. Chem. 25(12), 1463–1473 (2004).
Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Compu. Chem. 27(15), 1787–1799 (2006).
Scanlon, D. O. et al. Theoretical and Experimental Study of the Electronic Structures of MoO3 and MoO2 . J. Phys. Chem. C 114(10), 4636–4645 (2010).
Sitepu, H., O’Connor, B. H. & Li, D. Comparative evaluation of the March and generalized spherical harmonic preferred orientation models using X-ray diffraction data for molybdite and calcite powders. J. App. Crystal. 38(1), 158–167 (2005).
Greiner, M. T., Chai, L., Helander, M. G., Tang, W.-M. & Lu, Z.-H. Metal/Metal-Oxide Interfaces: How Metal Contacts Affect the Work Function and Band Structure of MoO3 . Adv. Funct. Mat. 23(2), 215–226 (2013).
Michaelson, H. B. The work function of the elements and its periodicity. J. Appl. Phys. 48(11), pp. 4729–4733 (1977).
KC, S., Longo, R. C., Addou, R., Wallace, R. M. & Cho, K. Impact of intrinsic atomic defects on the electronic structure of MoS2 monolayers. Nanotechnology 25(37), 375703 (2014).
KC, S., Longo, R. C., Wallace, R. M. & Cho, K. Surface oxidation energetics and kinetics on MoS2 monolayer. J. App. Phys. 117(13), p.135301 (2015).
Amani, M. et al. K. Near-unity photoluminescence quantum yield in MoS2 . Science 350(6264), 1065–1068 (2015).
Vasilopoulou, M. et al. The Influence of Hydrogenation and Oxygen Vacancies on Molybdenum Oxides Work Function and Gap States for Application in Organic Optoelectronics. J. Am. Chem. Soc. 134(39), 16178–16187 (2012).
Meyer, J. et al. Metal Oxide Induced Charge Transfer Doping and Band Alignment of Graphene Electrodes for Efficient Organic Light Emitting Diodes. Sci. Rep. 4, 5380 (2014).
Yamamoto, M., Nakaharai, S., Ueno, K. & Tsukagoshi, K. Self-Limiting Oxides on WSe2 as Controlled Surface Acceptors and Low-Resistance Hole Contacts. Nano Lett. 16, 2720 (2016).
Acknowledgements
We would like to thank Prof. Christopher Hinkle, Dr. Luigi Colombo, Dr. Stephen McDonnell, and Ms. Angelica Azcatl of UT-Dallas for useful discussions. We also thank Prof. A. Javey of UC Berkeley for motivating the modeling effort. This work was supported in part by the Center for Low Energy Systems Technology (LEAST), one of six centers supported by the STARnet phase of the Focus Center Research Program (FCRP), a Semiconductor Research Corporation program sponsored by MARCO and DARPA. Some of SK’s time completing this work was supported by the Department of Energy’s Office of Science, Materials Science and Engineering Division at Oak Ridge National Laboratory. Calculations were performed on Texas Advanced Computer Center (TACC) at University of Texas at Austin.
Author information
Authors and Affiliations
Contributions
KC, S. performed the DFT calculations and wrote the manuscript. R.C.L. and R.A. participated in discussion and in writing. R.M.W. and K.C. supervised this research. All the authors contributed in writing this manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
K. C., S., Longo, R., Addou, R. et al. Electronic properties of MoS2/MoOx interfaces: Implications in Tunnel Field Effect Transistors and Hole Contacts. Sci Rep 6, 33562 (2016). https://doi.org/10.1038/srep33562
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep33562
This article is cited by
-
Record-high saturation current in end-bond contacted monolayer MoS2 transistors
Nano Research (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.