Introduction

Owing to that fact that oxide semiconductor photocatalysts have promising applications in the development of renewable energy (e.g., converting solar energy into chemical fuels) and the treatment of environment pollution (e.g., degradation of pollutants), much attention has been paid to these materials over the past several decades1,2,3. One of the most popular oxide semiconductors for this purpose, titanium dioxide (TiO2), based on its high photocatalytic activity, resistance to photocorrosion, low cost and non-toxicity, has received intense research interest as a promising photocatalyst for water splitting and hydrogen production4,5. However, the intrinsic wide band gap of pure TiO2 (~3.2 eV for anatase and ~3.0 eV for rutile) confines its photon absorption to the ultraviolet (UV) region, severely limiting solar energy utilization to ~5%. Hence great efforts have been made to extend the photoabsorption of TiO2 to the visible light region5,6,7. Recently, silver-based oxides semiconductors are reported to own high photocatalytic activation in the visible light region, such as Ag3VO48, AgGaO29, AgSbO310. Especially, Ye et al.11 have found that Ag3PO4 exhibits strong oxidation power leading to O2 production from water, and the quantum yield achieve up to nearly 90% under visible light. This is intriguing because most photocatalysts give much poorer quantum yields of ~20%12. Therefore, further studies13,14,15,16,17 were carried out to understand the mechanism of its high water-oxidation activity. For example, Umezawa et al.18 revealed that the excellent photocatalytic performance of Ag3PO4 is attributed to the Ag s-s hybridization without localized d states which results in the highly dispersive band structure of the CBM of Ag3PO4. Although pure Ag3PO4 achieves an extremely high quantum yield under visible light, it has been recently found that native point defects are unlikely responsible for the electrical conductivity12. However, photoelectrochemical cell needs two-electrode to convert light energy into electric energy, e.g., metal cathode and photoanode made of n-type semiconductor16,19. Therefore, we expect that external doping can further improve the photocatalytic activity of this novel photooxidation material.

The valence-band maximum (VBM) of Ag3PO4 composes of mostly Ag 4d and O 2p states20. Oxygen is much more electronegative than the attempted nitrogen acceptor dopant, and the transition energy level of the NO acceptor should be high. Indeed, the calculated transition level for single acceptor NO is 0.4 eV above the VBM of Ag3PO417. On the other hand, since the cohesive energy of N2 is large, the chemical potential of N2 is very low and the formation energy of NO is very high21. To obtain net p-type Ag3PO4, the low solubility of N monodoping is unlikely to generate sufficient number of holes to compensate the free electrons. Successful p-type doping requires a shallow delocalized acceptor level. But doping generally destroys the local symmetry, and the chemical mismatch between the host and dopant may result in deep defect levels in the band gap22. The codoping method was originally proposed by Yamamoto and Katayama-Yoshida for carrier control in wide-band-gap semiconductors23. Using codoping method one may be able to enhance the dopant solubility and lower the defect transition energy levels. However, further study found that although codoping could be useful in increasing dopant incorporation, the different wave function characters and symmetry of donor and acceptor levels may result in a too weak repulsion between these levels, and codoping will fail to reduce the defect transition energy levels24,25. In order to decrease the ionization energy of N acceptor in ZnO, Yan et al.25 proposed the impurity band model to explain the real codoping mechanism. The essence of this model is the rise of the VBM. According to the “doping pinning rule”, the lower the VBM of a semiconductor is, the higher the probability that the semiconductor cannot be doped p-type is26. Moreover, Li et al.27 considered that the anion and cation kinetic p-d repulsion was one of the reasons why NO defect level is deep in ZnO, if replacing Zn atom by isovalent Mg or Be atom containing no d orbital, the defect transition energy level of nXZn-NO (X = Mg, Be, n = 1, 2, 3, 4) should be lower than that of NO in ZnO. But there is little studies on Li (without occupied d orbital) codoping in Ag3PO4, which will be addressed in this work.

In this present work, we used screened Coulomb potential hybrid DFT calculations to investigate the atomic structure and electronic properties of Cd, Li monodoping and (Cd, N), (Li, N) codoping in Ag3PO4. We calculate the formation energies and the transition energy levels of CdAg, CdP, CdO, Cdi, Cdi(s), the (CdAg-2NO) complex, LiP, LiO, Lii, Lii(s), and the (LiAg-NO) complex, as well as the binding energies of all defect complexes. The results show that CdAg and Lii (or Lii(s)) may serve as possible sources of n-type conductivity under O-poor conditions. CdAg is likely to bind with NO to form the (CdAg-NO) complex with a binding energy of −2.02 eV, and doping further N atom results in the (CdAg-2NO) complex, which acts as acceptor with a significantly smaller transition level compared to the isolated N acceptor in Ag3PO4.

Methods

Our calculations are based on DFT28 and projector-augmented wave potentials29 as implemented in the Vienna ab initio simulation package (VASP) code30. The exchange correlation potential is treated with the screened hybrid functional of Heyd, Scuseria, and Ernzerhof (HSE)31. We find that a proportion of 33% HF exchange with 67% PBE exchange produces accurate values for lattice constants and the band gap in Ag3PO4. The electron wave function was expanded in plane waves up to a cutoff energy of 300 eV and a Monkhorst-Pack k-point mesh32 of 2 × 2 × 2 was used for geometry optimization and electronic structure calculations. Both the atomic positions and cell parameters were optimized until residual forces were below 0.01 eV/Å. The optimized cell parameters are a = b = c = 6.02 Å, in excellent agreement with the experimental values of a = b = c = 6.00 Å20. The calculated indirect band gap (M−Γ) and the direct band gap (Γ) are 2.33 eV and 2.45 eV, in excellent agreement with the experimental value of 2.36 and 2.43 eV, respectively11. A 128-atom supercell is used to simulate Cd, Li monodoping and (Cd, N), (Li, N) codoping in Ag3PO4.

The likelihood of incorporating an impurity in Ag3PO4 is determined by its formation energy. In this paper, the formation energy of a charged defect is defined as the following:33

A more detailed discussion of the formation energy is described elsewhere34,35. When Ag3PO4 is grown under thermal equilibrium conditions, the chemical potentials of the constituent atoms, which is referenced to the values of their elemental forms, must satisfy the equilibrium condition 3μAg + μP + 4μO = ΔHf (Ag3PO4) = −10.46 eV, where ΔHf (Ag3PO4) is the formation enthalpy of Ag3PO4. In addition, we must enforce the constraint such as 2μAg + μO < ΔHf (Ag2O), to prevent the precipitation of Ag2O during the growing process of Ag3PO4. Similar constraint must be applied to P2O517. To avoid the precipitation of constituent atoms, μAg, μP, μO must satisfy μAg < 0, μP < 0, μO < 0, respectively. For impurity doping, the chemical potentials of impurities also need to satisfy other constraints to avoid the formation of impurities-related phases. Specifically, the chemical potential of Cd is constrained by μCd < 0 and μCd + μO < ΔHf (CdO) = −2.59 eV (experimental value36: −2.68 eV and theoretical value36: −2.40 eV). Also for Li doping, the chemical potential of Li is constrained by μLi < 0 and 2μLi + μO < ΔHf (Li2O) = −5.96 eV (experimental value37: −6.20 eV and theoretical value38: −6.28 eV). We take μN with respect to the energy per atom of N2 molecule.

The binding energy of a complex defect represents energy changing from isolated dopants to a complex defect. To determine whether the binding of two dopants is energetically preferred (e.g., CdAg and NO), we calculate the binding energy Eb, which is defined as39,40,41

where q1, q2, and q3 are the most stable charge states of CdAg, NO, and complex (CdAg-NO), respectively, at any given EF. A positive Eb indicates the reaction is exothermic and the defect pair tends to bind to each other when both are present in the system.

Results and Discussion

Cd monodoping

Cadmium sits to the right of Ag in the periodic table, having an atomic size very close to that of Ag which makes sure that negligible strain energy is introduced to the Ag3PO4 host. Thus, we expect Cd to preferentially occupy the Ag site in Ag3PO4, leading to relatively small relaxations and acting as a shallow donor. Indeed, in the neutral charge state (CdAg0), the neighboring O atoms relax inward, resulting in a Cd-O bond length (2.21 Å) that is 6.8% shorter than the equilibrium Ag-O bond length (2.37 Å), while the Cd-Ag bond length (3.22 Å) becomes 7% longer than the equilibrium Ag-Ag bond length (3.01 Å). In the positive charge state (CdAg+1), the Cd-O bond length is 2.2 Å, and the Cd-Ag bond length is 3.23 Å. It is noteworthy that the Cd-O bond length is similar to the counterpart (2.35 Å) in CdO unit cell42.

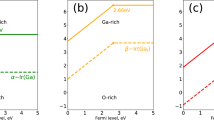
As expected, CdAg is shallow donor, and the transition energy level of ε(0/+) is located at 0.01 eV below the CBM. The conductivity of a semiconductor depends not only on the transition levels of donor or acceptors, but also on their formation energies. The results of formation energy for the defects under consideration are listed in Table 1. Figure 1 shows the calculated formation energies of CdAg as a function of Fermi level under O-rich [Fig. 1(a)] and O-poor [Fig. 1(b)] conditions, respectively. Under O-poor growth condition [Fig. 1(b)], the formation energy of CdAg is much lower than that under O-rich condition, and becomes negative in the entire range of EF value in the band gap. This is because the chemical potential of Cd is limited by the O chemical potential due to the limit of impurity-related phase CdO. Therefore, the highest possible μCd requires the lowest μO, i.e. O-poor condition. Our results suggest that n-type Ag3PO4 is achievable by Cd-doping under O-poor condition.

Table 1 Calculated transition energy levels and binding energies Eb of the defect complexes, and defect formation energies with EF = 0 under O-rich and O-poor conditions in Ag3PO4.
Full size table
Figure 1
figure 1

The formation energies of possible Cd monodoped defects, CdAg, CdP, CdO, Cdi and Cdi(s), together with (CdAg-2NO) complex as a function of the Fermi energy under O-rich (a) and O-poor (b) conditions. Only the lowest formation energy states are shown.

Full size image

When Cd dopant occupies the P lattice site, this defect behaves as a triple acceptor. The transition energy levels of ε(−/0), ε(2−/0) and ε(3−/0) are located at 0.13 eV, 0.27 eV and 0.25 eV above the VBM, respectively. In general, deep impurity-related levels typically represent localized electron distributions, and a change of occupancy usually results in change of structures43. Indeed, because of the large size mismatch between the Cd and P atoms, the four oxygen neighbors of CdP lie at a distance of 2.20–2.21 Å, which are larger than the equilibrium P-O bond length of 1.56 Å for bulk Ag3PO4. As seen in Fig. 1, the formation energy of CdP is quite high even under extreme O-rich condition. Moreover, recent studies, based on a revised molecular orbital diagram for Ag3PO4, have pointed out that the strong covalent interactions are formed in the tetrahedral PO4 structural units14. It is therefore not expected that Cd will incorporate on the P site with an appreciable solubility.

Since oxygen atom can provide six electrons and cadmium can provide only two electrons, it is expected that CdO acts as donor. Indeed, the calculated transition energy levels of ε(0/+), ε(0/2+), ε(0/3+) and ε(0/4+) are located at −0.02 eV, −0.24 eV, 0.53 eV and 0.91 eV below the CBM, respectively. For CdO, in the 0, 1+, 2+, 3+ and 4+ charge states, the distances between Cd and the nearest-neighbor O atoms are 3.32, 3.05, 2.88, 2.86 and 2.84 Å, respectively. This dramatic lattice distortion can lead to higher formation energy. According to Fig. 1, CdO has much lower formation energy under O poor condition than under O rich condition. But even under O poor condition, CdO has a formation energy that is 1.91 eV higher than that of CdAg at the VBM, and so its contribution is less significant.

For interstitial Cd, we have studied two possible atomic configurations. One is the tetrahedral site coordinated by four O atoms (expressed as Cdi), the other is the so-called split interstitial site which consists of two atoms on a single substitutional lattice site (expressed as Cdi(s)), as shown in Fig. 2. For Cdi(s), this configuration is 0.16 eV higher in energy than Cdi, and the calculated transition energy levels of ε(0/+) and ε(0/2+) are located at 0.27 eV and 0.14 eV below the CBM, which are 0.17 eV and 0.13 eV higher than that of Cdi, respectively. Therefore, in the following discussion we consider only the Cdi configuration. In the neutral charge state, the distance between Cd and the nearest-neighbor O atom is 2.33 Å which is very close to the Cd-O bond length in CdO unit cell. In the 1+ and 2+ charge states, the Cd-O bond lengths are 2.29 and 2.26 Å, respectively. As shown in Fig. 1, the calculated formation energies of Cdi2+ are −0.14 and −1.83 eV under O-rich and O-poor conditions at the VBM, respectively. It implies that O-poor condition would produce much more abundant numbers of Cd donors in comparison with O-rich condition. However, its formation energy is relatively high compared with that of CdAg under both O-rich and O-poor conditions, regardless of the Fermi level position. Our results indicate that Cdi will not be a relevant configuration for Cadmium in Ag3PO4.

Figure 2
figure 2

Atomic geometry of the relaxed structures of the (a) Cdi and (b) Cdi(s) configurations in Ag3PO4.

Full size image

Cd codoping

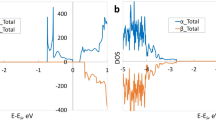
The formation of the (CdAg-NO) complex is a result of Coulomb binding between positively charged donor (CdAg) and negatively charged acceptor (NO). To see if the complex can form, we calculated the binding energy. We find that CdAg is likely to bind with NO to form the (CdAg-NO) complex with a binding energy of 0.03 eV. The positive binding energy means that the complex is energetically favorable and can be seen as the passive complex. Obviously, the (CdAg-NO) complex is dielectric and will not provide electron or hole in Ag3PO4. But it may affect the electrical properties by changing the electronic structure44. The values of Eb for this complex are shown in Fig. 3 as a function of the Fermi level. Figure 4 shows the calculated total DOS of Ag3PO4 with and without the (CdAg-NO) complex in order to see the effect of passivation on relative shift of the VBM. As can be seen from Fig. 4, the formation of a passive (CdAg-NO) complex does not change the basic electronic structure, but only generates an additional fully occupied impurity band with the energy width of 0.54 eV above the VBM of Ag3PO4. The distance between Cd and N in the complex is 2.14 Å. The bond length of Cd and its nearest-neighbor O atom is 2.18 Å, which is 8% shorter than the equilibrium Ag-O bond length. The Cd-Ag bond length (3.01 Å) becomes 2% longer than the equilibrium Ag-Ag bond length.

Figure 3
figure 3

Binding energies Eb of complex defects as a function of the Fermi level.

Full size image
Figure 4
figure 4

The calculated total DOS for pure Ag3PO4 and a supercell containing a (CdAg-NO) complex.

Full size image

When a second N atom is added to a neighbor site of the passive (CdAg-NO) complex (the configuration of CdAg-2NO complex is shown in Fig. 5), we find that the binding energy of (CdAg-2NO) is 0.51 eV with respect to the (CdAg-NO) complex and NO. The positive binding energy means that the p-type complex is energetically stable and can form if more acceptors are doped into Ag3PO4. Based on the fact that the transition will occur between the N defect levels and the fully occupied impurity bands rather than the original valence band25, we calculated the transition energy level ε(−/0) of (CdAg-2NO) which is 0.49 eV above the VBM of Ag3PO4. And the value is reduced to −0.05 eV from the impurity band of the passive (CdAg-NO) complex. Therefore, the transition level can be reduced dramatically. In the neutral charge state (CdAg-2NO)0, the distances between Cd and N1, Cd and N2 atoms in the complex are 2.16 and 4.09 Å, respectively. The bond lengths of Cd-O and N1-P are 2.18 and 1.65 Å, which are 8% shorter and 5.8% longer than the Ag-O and O-P bond lengths in the bulk, respectively. The distance between Cd and Ag is 3.12 Å along the b axis, which is 3.7% longer than the corresponding bond length of Ag-Ag in bulk Ag3PO4. Whether a dopant can be a good acceptor, it should have high solubility under proper conditions, except low transition energy. Figure 1 has depicted the calculated formation energies as a function of Fermi level for (CdAg-2NO) under O-rich and O-poor conditions, respectively. We can see that the formation energy of the (CdAg-2NO) acceptor is relatively high even under O-poor condition. If the formation energy is higher than that of the corresponding single points defects CdAg and NO17, it is because the energy cost to create the extra single point defect is larger than the Coulomb interaction between the donors and acceptors24. Thus, p-type conductivity would not be readily achieved by (Cd, N) codoping of Ag3PO4.

Figure 5
figure 5

Crystal structure of Ag3PO4 supercell with codoping of CdAg and two NO.

The silver, pink, red, khaki and blue balls represent Ag, P, O, Cd and N atoms, respectively.

Full size image

From what has been discussed above, CdAg is suggested to be the dominant donor in Cd-doped Ag3PO4. Combined with the fact that “electron killer” is Ag vacancy (VAg)16, the natural candidate for a possible complex is the CdAg donor and VAg acceptor pair. Indeed, our hybrid functional calculations indicate that the (CdAg-2VAg) complex is an acceptor with the transition level ε(−/0) of 0.18 eV above the VBM. In order to increase the distance between two VAg and weaken the level repulsion between them, we have established a configuration that two VAg acceptors are connected by CdAg donor, as proposed by Limpijumnong et al.45 in ZnO (AsZn-2VZn). However, the binding energy for the (CdAg-2VAg) complex is negative at −0.08 eV. It implies that this kind of defect complex is unlikely to exist in Ag3PO4.

Li monodoping

Since Li and Ag are isovalent, Ag substituted by Li (LiAg) is electrically inactive and Li monodoping is not considered. Similar to CdP, LiP has rather high formation energies under both O-rich and O-poor conditions (as shown in Fig. 6) because of the strong covalent interaction in the PO4 units, which indicates that the formation of LiP is energetically unfavorable. The calculated results are summarized in Table 1. In the neutral charge state, the four equivalent oxygen atoms move outward by 25% of the initial P-O bond length. For Li substituting O (LiO), the calculated formation energies of LiO are lower than LiP, mainly because of the small misfit of atomic radius. The distance between Li and the nearest-neighbor O atom is 1.9 Å in the neutral charge state, and this highly perturbed structure can be described as Li going to an interstitial site and leaving behind an O vacancy43. The calculated transition energy levels ε(0/+), ε(0/2+) and ε(0/3+) are located at 0.18 eV, 1.55 eV and 2.0 eV below the CBM, respectively.

Figure 6
figure 6

The formation energies of possible Li monodoped defects, LiP, LiO, Lii and Lii(s), together with (LiAg-NO) complex and (LiAg-VAg) complex as a function of the Fermi energy under O-rich (a) and O-poor (b) conditions. Only the lowest formation energy states are shown.

Full size image

Although substitutional Li behaves as an acceptor, Li tends to occupy the interstitial site and loose its outmost electron to behave as a donor. This will lead to the self-compensation and limit its application as an efficient p-type dopant in ZnO27. Therefore, we have also studied two possible atomic configurations for interstitial Li as shown in Fig. 7. The most stable configuration is the split interstitial doping and Lii(s) is only 0.06 eV lower in energy than Lii. The calculated transition energy level ε(0/+) for Lii and Lii(s) are found to lie at 0.04 and 0.15 eV above the CBM, respectively. Figure 6 shows the calculated defect formation energy as a function of the Fermi level under O-rich and O-poor conditions. From Fig. 6, it was found that Li impurity prefers interstitial sites over substitutional sites regardless of the Fermi level position. For example, the formation energy of Lii (Lii(s)) is 2.21 eV (2.38 eV) lower than that of LiO under O-poor condition. However, the formation energies of the positively charged interstitial Li (Lii or Lii(s)) increase with the Fermi energy while the negatively charged complex (LiAg-VAg) decrease with the Fermi energy and the (LiAg-VAg) complex is not stable (see discussion later). Our analysis suggests that interstitial Li (Lii or Lii(s)) is likely to be the n-type dopant under O-poor condition.

Figure 7
figure 7

Atomic geometry of the relaxed structures of the (a) Lii and (b) Lii(s) configurations in Ag3PO4.

Full size image

Li codoping

Because LiAg is electrically inactive and NO is a deep acceptor, the (LiAg-NO) complex is an acceptor. The calculated transition energy level ε(−/0) for the complex is located at 0.54 eV above the VBM, deeper than the corresponding single N dopant (0.46 eV)17. It is because the radius of Li is very different from Ag. To make sure whether the complex can form, we have also calculated the binding energy. The calculated binding energy for the (LiAg-NO) complex is negative (−0.11 eV), indicating that LiAg will not bind with NO in Ag3PO4. This is likely because the Ag-N bond is stronger than the Li-N bond. According to our calculations, the Ag-N bond length (2.11 Å) is shorter than the Li-N bond length (4.61 Å). It should be that the stable p-type conductivity will not be achieved by the (LiAg-NO) complex. We also calculated the transition energy level ε(−/0) for the (LiAg-VAg) complex, which is located at 0.04 eV below the VBM. The binding energy of this complex is positive (0.04 eV), which implies that this complex is stable in Ag3PO4.

Conclusions

In summary, we have investigated the formation of isolated defects and defect complexes in Cd and Li monodoped, (Cd, N) and (Li, N) codoped Ag3PO4 by the hybrid functional calculations. It is found that CdAg contributes to the n-type conductivity of Ag3PO4 under O-poor conditions. For CdP and CdO, both of the two configurations will not be the relevant configurations for Cd doping in Ag3PO4, on account of the strong covalent interactions in the tetrahedral PO4 structural units. For interstitial Cd (Cdi), the calculated formation energy is relatively high compared with that of CdAg donor. Our results demonstrate that Cd can bind to N atom to form a stable passive (CdAg-NO) complex. Although the transition energy level of the acceptor (CdAg-2NO) complex is reduced from 0.49 to −0.05 eV when electrons are transited from the impurity band of the passive complex rather than the original valence band, the formation energy of the acceptor complex is high in comparison with the isolated NO. Same as CdP and CdO, LiP and LiO will not be the relevant configurations for Li doping in Ag3PO4. But interstitial Li (Lii or Lii(s)) with suitable level and appreciable solubility is likely to be the n-type dopant under O-poor condition. For the (LiAg-NO) complex, the calculated binding energy is negative (−0.11 eV) because the Ag-N bond is stronger than the Li-N bond. While, the (LiAg-VAg) complex is potentially to be the p-type dopant under O-rich condition.

Additional Information

How to cite this article: Huang, Y. et al. Cadmium and lithium doping in silver orthophosphate: An ab initio study. Sci. Rep. 6, 32574; doi: 10.1038/srep32574 (2016).