Abstract
Humans benefit from extensive cooperation; however, the existence of free-riders may cause cooperation to collapse. This is called the social dilemma. It has been shown that punishing free-riders is an effective way of resolving this problem. Because punishment is costly, this gives rise to the second-order social dilemma. Without exception, existing solutions rely on some stringent assumptions. This paper proposes, under very mild conditions, a simple model of a public goods game featuring increasing returns to scale. We find that punishers stand out and even dominate the population provided that the degree of increasing returns to scale is large enough; consequently, the second-order social dilemma dissipates. Historical evidence shows that people are more willing to cooperate with others and punish defectors when they suffer from either internal or external menaces. During the prehistoric age, the abundance of contributors was decisive in joint endeavours such as fighting floods, defending territory, and hunting. These situations serve as favourable examples of public goods games in which the degrees of increasing returns to scale are undoubtedly very large. Our findings show that natural selection has endowed human kind with a tendency to pursue justice and punish defection that deviates from social norms.
Similar content being viewed by others
Introduction
It was only approximately 12,000 years ago, with the emergence of agricultural civilization in Mesopotamia, that individuals and families alike were able to play primary roles in economic activities1. In other words, in more than 99% of the 7 million years of human evolutionary history2, our ancestors had to rely on joint endeavours rather than individuals or families to maintain species survival. This life pattern includes joint projects such as hunting large game, fighting natural disasters, defending territory against invaders, and, most importantly, sharing the fruits of these cooperative activities3,4,5. This life pattern can be viewed as a particular mechanism for producing and distributing public goods.
Public goods games (PGGs) have been widely employed to investigate the evolution of human cooperation within the framework of evolutionary game theory. In a standard PGG, the total return of a joint project is divided equally among all participants, which means that a defector can free-ride other participants and hence can fare better than others. This situation raises an evolutionary puzzle: how do cooperators rise and evolve? Because the payoff of a cooperator is strictly lower than that of a defector, each participant, in light of the hypothesis of self-interest, chooses to contribute nothing to the PGG in Nash equilibrium. As a result, any individual’s payoff will be zero. This is called the social dilemma6,7.
It is widely believed that punishing defection serves as an effective way to resolve this problem. Assume that some players, called punishers or altruistic punishers, have a strong sense of justice and not only contribute but also punish those who deviate from social norms. If the strength of punishment exceeds the contribution cost, free-riding becomes unprofitable, and the PGG is immune from the social dilemma8,9,10,11,12,13. Related anthropological and zoological studies show that punishing defection was not only an important way for human beings to maintain cooperation in early societies14,15 but is also a vital means for many types of animals to maintain species survival16,17.
However, punishment is costly because it takes time and energy and invites retaliation. As a result, the payoff of a punisher is lower than that of a cooperator. In light of the hypothesis of self-interest, each participant will choose to co-operate but not punish in Nash equilibrium. These cooperators are called second-order free-riders to distinguish them from defectors. This situation presents a second evolutionary puzzle for humankind: how do punishers rise and evolve? Once punishers are invaded by cooperators, defectors can easily invade and dominate the population; thus, defection eventually prevails in the evolutionary equilibrium. This is called the second-order social dilemma8,18,19,20.
From the perspective of the evolution of simulation, there are two main types of relevant studies to solve the problem of the second-order social dilemma. One type is based on the viewpoint of the social network21,22,23,24, including different mechanisms of punishment, such as adaptive punishment25, probabilistic punishment26,27, and conditional punishment28. Reward is another solution to the second-order social dilemma29. The use of a combination of rewards and punishment is also an important method30,31,32,33. The evolutionary games of spatial networks not only provide an important perspective for solving the problem of the first-order social dilemma34,35 but also shed light on the solution for the second-order social dilemma.
The second categorization relates to the agent-based model, but none of these models is immune from some strong conditions: (i) external conditions, including the group selection effect resulting from immigration36,37, indirect reciprocity that is dependent on the reputation mechanism38,39, and the effect of cultural selection40,41 or religious indoctrination42,43; and (ii) internal conditions, including the addition of new strategies or new types of behaviour to alter the payoff matrix of the game, such as voluntary participation44,45, rewards46, sympathy47, and pool punishment48 or the modification of game rules that may change the nature of the game, such as communication45, coordination49, and cooperation50 among punishers. These strong conditions inevitably narrow our scope of interpretation51.
In accordance with the intrinsic properties of human co-operation, we propose a model of PGG without imposing any further assumptions (including new strategies, behaviour types, or game rules) to resolve the second-order social dilemma. It is well known that one of the most important properties of human cooperation is economies of scale51,52.
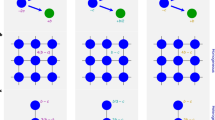
As an example, Fig. 1 shows collective hunting in a primitive society. Assume that both the number of the prey per unit area and the length a hunter is able to siege are given. In this case, the hunting returns will depend on the area controlled by the hunters and, ultimately, on the number of hunters. Let l denote the length a hunter is able to siege. Then, n hunters can siege an area with a circumference of nl, and they can control at best an area of (l2/4π)n2. Therefore, the return of adding one more hunter to this hunting activity grows exponentially. Such a scenario is termed “economies of scale” or “increasing returns to scale”.
According to the aforementioned discussion, we construct a general model of PGG featuring increasing returns to scale. Our analysis of the stochastic evolutionary dynamics and the corresponding computer simulations show that punishers will achieve dominating evolutionary advantages and are able to resist any invasion of second-order free-riders provided that the degree of increasing returns to scale is sufficiently large. Thus, the second-order social dilemma can be effectively resolved.
Results
Analytical results
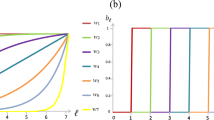
We establish a stochastic evolutionary model of PGG in a finite population. To see the effect of an economy of scale, we calculate the relative time of cooperators (X), defectors (Y) and punishers (Z) in homogeneous states as a function of the coefficient of increasing returns to scale (denoted as α). The relative time in homogeneous states means the probability of the population being occupied entirely by one of the three strategies. The parameters in the model are population size (M), sample size (N), contribution cost(c), multiplier of return (r), strength of punishment (δ), cost of punishment (γ), selection strength (ω) and mutation rate (μ). The results are plotted in Fig. 2 below.
As seen in the figure above, in the stochastic evolutionary model, both punishers and cooperators become increasingly dominant relative to defectors if the coefficient of increasing returns to scale α ≥ 1.3. Punishers and cooperators even jointly dominate the population and are unlikely to be invaded by defectors when α ≥ 1.6. In this case, defectors almost certainly become extinct. Because punishment is no longer necessary, cooperators and punishers fare the same. Consequently, the second-order social dilemma dissipates.
Simulation results
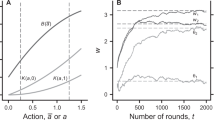
We also adopt a frequency-dependent Moran process to specify the stochastic dynamics of a PGG in a finite population and run a series of multi-agent computer simulations. Our computer simulations show that the punishing strategy cannot gain a foothold in the population if the PGG is of constant returns to scale (α = 1). Typically, a rock-paper-scissors-like evolution path governed by the alternating temporary domination of each type will emerge, so the system is unable to form stable cooperation (Fig. 3a). However, punishment becomes the only evolutionarily dominant strategy of the three types in the population provided that the degree of increasing returns to scale of the PGG is sufficiently large (for example, α = 1.8). The resulting evolution path shows that after a number of transient oscillations, punishers immediately come to dominate the population and can resist the invasion of any other strategy (Fig. 3b). This implies that the second-order social dilemma dissipates in the PGG featuring increasing returns to scale.
Robust tests
The simulation results in Fig. 3 are robust when we extend the periods to more than 1 million or change the initial composition of the population. The simulation was repeated 20 times, and all displayed a similar montage. As a result, we randomly chose one as the representative montage of the simulation result.
To further test the robustness of the results obtained, we studied how different parameter values can affect the evolution of cooperation in a PGG (Fig. 4). The strategy frequency here is the averaged proportion of different strategies in the population in 100,000 periods. All of the results are averaged over 20 times, and they are not affected by the initial composition of the population.
(a ~ c) coefficient of increasing returns to scale α in different initial composition: (a) 100% cooperators, (b) 100% defectors, (c) 100% punishers; (d) multiplier of return r; (e) contribution cost c; (f) strength of punishment δ; (g) cost of punishment γ; (h) selection strength ω; (i) mutation rate μ. The parameter values are X = 30, Y = 40, Z = 30 (except for figure a ~ c), r = 3 (except for figure d), c = 1 (except for figure e), α = 1.0 (except for figure d), α = 1.8 (except for figure a ~ c), δ = 1 (except for figure f), γ = 0.3 (except for figure g), ω = 0.5 (except for figure h), μ = 0.001 (except for figure i).
We can see that there is a threshold value of α of approximately 1.2 in which the punishers and the defectors are very similar. When α is larger than 1.2, the punishers can gradually gain an advantage against both the defectors and the cooperators. The multiplier of return r has a similar effect as α. Moreover, increasing the cost of contribution and punishment has a negative effect on the maintenance of cooperation, whereas increasing the strength of punishment, the selection strength and the mutation rate helps the punishers in defeating the defectors, which in turn has corresponding effects on the threshold value of α. Due to space limitations, other robust tests on various parameters can be found in the Supplementary Materials (Fig. S2–S12).
Discussion
The underlying mechanism of increasing returns to scale to solve the second-order social dilemma
Why do punishers fare best in the PGG with increasing returns to scale, hence resolving the second-order social dilemma? It is well known that punishers are primarily threatened by cooperators’ second-order free-riding. However, by analysing the simulation data, we find that the payoff advantage of cooperators over punishers diminishes as the degree of increasing returns to scale becomes larger. This is because the larger the degree of increasing returns to scale is, the higher the payoff each individual receives from the game. Given that the punishment cost is held fixed, the payoff difference between punishers and cooperators sharply decreases as the average payoff of all individuals increases, indicating that the evolutionary advantage of cooperators over punishers becomes very small (see Supplementary Materials, Fig. S13). When such an advantage becomes sufficiently weak, it is very likely to be offset by the randomness in evolutionary dynamics.
This randomness in the biological evolutionary process is primarily due to genetic variation inside the organism and genetic drift induced by environmental factors. This suggests that biological character is not determined entirely by fitness. Rather, with small probability, it is affected by random disturbances from inside or outside the organisms. If the evolutionary advantage of a particular biological character is large enough, it can successfully resist this random disturbance. Otherwise, its evolutionary advantage will eventually be offset by the random disturbance.
Of course, this randomness affects each type of player. However, our computer simulations show that only punishers, rather than cooperators, can dominate the population. This finding seems to suggest that randomness only weakens the advantage of cooperators. Further analysis of the simulation data shows that cooperators may dominate the population only for transient periods, but eventually they cannot defend their regime because defectors can easily invade and dominate the population.On the contrary, the evolutionary advantage of punishers is reinforced once they become dominant in the population. This is because the abundance of punishers effectively restrains the spread of defectors, reducing the punishment cost. As a result, punishers’ evolutionary advantage becomes even more dominant (see Supplementary Materials, Fig. S14). Therefore, as shown in our computer simulation, once the punishers establish their regime in the population, it becomes extremely difficult for other types to invade.
The historical evidence of increasing returns to scale
Modern production activities depend not only on labour but also on many other production factors, including capital and technology. However, many large-scale production activities in modern society still depend heavily on the number of cooperators. The number of participants has a great impact on the results of activities. In fact, revenue grows exponentially with the number of participants. Examples of such activities include conventional warfare, geological exploration, and rescue activities during natural calamities such as earthquakes, tsunamis, and floods. As rarely as these events may be considered in modern society, the degrees of increasing returns to scale are usually extremely large in these activities. Our model provides a reasonable interpretation of why individuals are more willing to reach a consensus to cooperate and punish defectors under these circumstances.
In a primitive society in which the level of productivity is extremely low, labour becomes the most important or even the only production factor1. The number of contributors thus plays a decisive role in many joint endeavours in a primitive society, such as fighting floods, defending territory, and hunting large game. The degrees of increasing returns to scale are all very large in these activities52. Therefore, increasing returns to scale may have been a common feature in most social activities over the prehistorical age, lasting for millions of years.
Ample evolutionary psychology studies have suggested that the mind, and thus the behaviour, of modern man has long been formed by the ancestral environment53 because agricultural civilization has a history of only a little more than 10,000 years and industrial civilization is less than 300 years old, whereas human society has millions of years of history. Neuroanatomy evidence also shows that the interconnections among neurons in the human brain have changed very little since the Industrial Revolution. Thus, it may not be surprising that some evolutionary psychologists claim that “our modern skulls house a stone age mind”54. These facts help us better understand why the pursuit of fairness and justice has become a common psychological state and the behavioural propensity of human beings. Our results show that natural selection has endowed humankind with a tendency to pursue justice and to punish defectors who deviate from social norms. In other words, the sense of justice is a product of long-lasting human evolution.
Methods
A model of a PGG featuring increasing returns to scale
We can apply a Cobb-Douglas production function P = cr(X + Z)αYβ to characterize the PGG with increasing returns to scale55,56, where P denotes total payoff from the PGG, c is the contribution cost to the joint project from each contributor (including cooperators and punishers, c > 0), r the multiplier of return (r > 1), X the number of cooperators, Z is the number of punishers, Y is the number of defectors, and α and β are the contribution rate of contributors and defectors, respectively. Because cr > 0, the PGG is featured with increasing returns to scale if α + β > 1. Moreover, because defectors make no contribution, namely, β = 0, the PGG features increasing returns to scale provided that α > 1. In this case, α is called the coefficient of increasing returns to scale.
Let δ and γ denote the strength and the cost of punishment, respectively. Then, the payoffs of cooperators, defectors, and punishers from each period, namely, Px, Py and Pz,from a PGG with increasing returns to scale are given below:



A stochastic evolutionary model of a PGG with finite population
As a useful method to analyse the stochastic evolutionary process of a finite population, the Moran process is widely applied in studies of biological evolution and evolutionary game theory, e.g., genetic replication, genetic mutation, genetic drift, or strategy learning and updating57,58,59,60.
The analysis of the stochastic evolution of a finite population will be greatly simplified in the limiting case, the mutation rate μ → 0, where the population consists of two types at most. For μ = 0, any monomorphic state becomes absorbing. If the mutation rate μ is sufficiently small, a mutant either becomes extinct or spreads into fixation before the next mutant appears. Therefore, the transition between any two monomorphic states occurs only when a mutant appears and spreads into fixation. In this case, the multivariate hypergeometric sampling reduces to a hypergeometric distribution44.
Next, consider a sampling process of randomly choosing N individuals from a well-mixed finite population of constant size M to participate in a PGG with increasing returns to scale. For μ → 0, this process is equivalent to an N-trial sampling without replacement from a population with mi individuals of type i and mj = M-mi individuals of type j. The probability of selecting k individuals of type i and N-k individuals of type j is

Thus, according to equation (4) and the model of the PGG (1)-(3), in any period of the game, for the X cooperators and Y = M-X defectors, the expected payoff Pxy of cooperators competing against defectors and the expected payoff Pyx of defectors competing against cooperators are


Similarly, the expected payoffs to punishers and defectors are


Finally, the expected payoffs to cooperators and punishers are

The evolutionary fitness fij of an individual of type i in a well-mixed population of types i and j can be calculated from its payoff Pij and the fitness function F = exp(ωP), which is

Thus, the probability of changing the number of individuals of type i by ±1, Tij±, can be calculated


from these transition probabilities, the fixation probability ρij of a single mutant strategy of type i in a resident population of type j can be derived (see Appendix A):

Consequently, the fixation probabilities ρij define the transition probabilities between the three different homogeneous states of the population. The corresponding Markov transition matrix A is given by

The normalized right eigenvector to the largest eigenvalue (which is 1) of the transposed matrix of A determines the stationary distribution; that is, it indicates the probability of finding the system in one of the three homogeneous states. It is given by (see Appendix B)

The normalization factor N must be chosen such that the elements of ø sum up to one.
Simulation
When μ > 0 and is not negligible, the fixation probabilities generally continue to fluctuate because of the existence of random disturbance. However, as long as some behaviour or character is evolutionarily stable, its regime in the population will eventually withstand any random disturbance. Here, we adopt a frequency-dependent Moran process to specify the stochastic dynamics of PGG in a finite population44,45,47 and run a series of multi-agent computer simulations with μ > 0. The computer simulation procedures are specified as below.
-
1
Setting a random sample to participate in the game. Applying the Monte Carlo method60,61,62, N individuals are randomly chosen from a well-mixed finite population of constant size M to participate in a PGG with increasing returns to scale.
-
2
Calculating the payoffs from the game. Let the individuals from the sample play the game, and then use computer simulation software to calculate the payoff of each type of player at the end of each period of the game according to equations (1–3).
-
3
Calculating evolutionary fitness. A basic assumption of evolutionary game theory is that individuals are more prone to imitate those with higher payoffs. This assumption implies that individuals with higher payoffs generally have higher fitness and are thus more evolutionarily advantageous. In evolutionary dynamics, a commonly used algorithm to calculate fitness is F = 1 − ω + ωP, where F denotes fitness, P is payoff, and ω is selection strength (0 < ω ≤ 1). This algorithm treats fitness as a convex combination of the “baseline fitness”, which is normalized to 1 for all players, and the payoff from the game44. A drawback of this algorithm is that it is only applicable for analysing stochastic evolutionary dynamics under weak selection because fitness may be negative for strong selection. To avoid this limitation, we adopt an exponential function F = exp(ωP) by Thaulsen et al.63 in our computer simulation, which allows us to accommodate any value of ω in its domain.
-
4
Genetic replication or strategy updating. The Moran process assumes that one member of the population M is chosen to die and is replaced by a newly born individual in each generation of the evolutionary process. The type of the newly born individual is jointly determined by both the fitness and frequency of each type of individuals in the population. Usually, two algorithms are commonly used to implement the above process44,59. The first is the “birth-death” process in which an individual is first chosen for reproduction with a probability proportional to its fitness, and then its clonal offspring replaces a randomly selected individual from the population M. The second is the “death-birth” process, in which a randomly selected individual is first removed from the population M and another individual is subsequently selected for reproduction with a probability proportional to its fitness and produces a clonal offspring. In addition to these algorithms, we apply a third approach called “genetic pool” in our computer simulations, in which each individual in the population M reproduces an offspring with a probability proportional to its fitness, and these newly born individuals form a “genetic pool” from which one offspring is chosen randomly to replace an individual in the population47,59.
-
5
Genetic variation or mutation. Genetic variation is an important factor that affects the evolutionary process. A common assumption of evolutionary dynamics is that any individual of a specific type can switch to another type with a small probability μ irrespective of its payoff. The parameter μ is called the mutation rate. This assumption implies that players will change their strategies with a very small probability without taking the potential payoffs of alternative strategies into account, which can simply be viewed as players’ tentative exploration of alternative strategies44.
The aforementioned steps are executed successively and compose our multi-agent computer simulations based on the frequency-dependent Moran process (see Supplementary Materials, Fig. S1).
Appendix A: Proof of equation (13)
Let n denote the state that has n individuals of type i. From n = 0 to n = M, there are M + 1 kinds of states in total, the transitions between which compose the Markov process. The states of n = 0 and n = M are absorbing states. The corresponding Markov transition matrix is

Suppose xk is the probability of the state k transiting to the absorbing state M; thus, we can obtain

So, if we let yk = xk − xk−1, θk = tk−/tk+, we can obtain

This means that y1 = x1, y2 = θ1 × 1, y3 = θ1θ2 × 1, and so on. We can also obtain the following identity:

Substituting equation (A.2) into the identity, we can obtain

Here, x1 donates the probability of the state that has a mutant of type i transiting to the state completely dominated by this type, which is exactly the fixation probability ρij we want. Substitute θ and equation (10) into equation (A.3), and we can obtain equation (13).
Appendix B: Proof of equation (15)
For a Markov transition matrix P = (Pij), a probability distribution {πi, i ≥ 0} is called the stationary distribution of the Markov chain if it satisfies

It can be rewritten as

Taking the transpose of both sides, we can obtain

The transposed matrix of the Markov transition matrix A is

Substituting equation (B.2) into equation (B.1) and with some calculations, we can obtain the following homogeneous linear equations:

Remember that {πi, i ≥ 0} is a probability distribution, which means the identity

Substituting the identity into equation (B.3), we can obtain equation (15).
Additional Information
How to cite this article: Ye, H. et al. Increasing returns to scale: The solution to the second-order social dilemma. Sci. Rep. 6, 31927; doi: 10.1038/srep31927 (2016).
References
Winch, P. Understanding a primitive society. Am. Philos. Quart. 1, 307–324 (1964).
Brunet, M. et al. A new hominid from the upper Miocene of Chad, Central Africa. Nature 418, 145–151 (2002).
Marlowe, F. W. et al. The ‘spiteful’ origins of human cooperation. Proc. R. Soc. B. 278, 2159–2164 (2011).
Boyd, R., Silk, J. B., Walker, P. L. & Hagen, E. H. How humans evolved (4rd ed.) 123–124 (Norton, 2006).
Feinman, S. An evolutionary theory of food sharing. Soc. Sc. Inform. 18, 695–726 (1979).
Dawes, R. M. Social dilemmas. Annu. Rev. Psychol. 31, 169–193 (1980).
Kollock, P. Social dilemmas: the anatomy of cooperation. Annu. Rev. Sociol. 24, 183–214 (1998).
Fehr, E. & Gächter, S. Altruistic punishment in humans. Nature 415, 137–140 (2002).
Henrich, J. et al. Costly punishment across human societies. Science 312, 1767–1770 (2006).
Hilbe, C. & Traulsen, A. Emergence of responsible sanctions without second order free riders, antisocial punishment or spite. Sci. Rep. 2 (2012).
Gintis, H. Punishment and cooperation. Science 319, 1345–1346 (2008).
Gao, L., Wang, Z., Pansini, R., Li, Y. T. & Wang, R. W. Collective punishment is more effective than collective reward for promoting cooperation. Sci. Rep. 5 (2015).
Chen, X. J., Sasaki, T. & Perc, M. Evolution of public cooperation in a monitored society with implicated punishment and within group enforcement. Sci. Rep. 5, 17050 (2015).
Gruter, M. & Masters, R. D. Ostracism as a social and biological phenomenon: An introduction. Ethol. Sociobiol. 7, 149–158 (1986).
Wiessner, P. Norm enforcement among the Ju/‘hoansi bushmen: A case of strong reciprocity? Hum. Nat. 16, 115–145 (2005).
Clutton-Brock, T. H. & Parker, G. A. Punishment in animal societies. Nature 373, 209–216 (1995).
Wong, M. Y., Buston, P. M., Munday, P. L. & Jones, G. P. Threat of punishment enforces peaceful cooperation and stabilizes queues in a coral-reef fish. Proc. R. Soc. B. 274, 1093–1099 (2007).
Yamagishi, T. The provision of a sanctioning system as a public good. J. Pers. Soc. Psychol. 51, 110–116 (1986).
Fowler, J. H. Human cooperation: second-order free-rider problem solved? Nature 437, E8–E8 (2005).
Colman, A. The puzzle of cooperation. Nature 440, 744–745 (2006).
Helbing, D., Szolnoki, A., Perc, M. & Szabó, G. Evolutionary establishment of moral and double moral standards through spatial interactions. PLoS Comput. Biol. 6, e1000758 (2010).
Perc, M. & Szolnoki, A. Coevolutionary games - A mini review. BioSystems 99, 109–125 (2010).
Helbing, D., Szolnoki, A., Perc, M. & Szabó, G. Punish, but not too hard: how costly punishment spreads in the spatial public goods game. New J. Phys. 12, 083005 (2010)
Szolnoki, A., Szabó, G. & Perc, M. Phase diagrams for the spatial public goods game with pool punishment. Phys. Rev. E 83, 036101 (2011).
Perc, M. & Szolnoki, A. Self-organization of punishment in structured populations. New J. Phys. 14, 043013 (2012).
Chen, X., Szolnoki, A. & Perc, M. Probabilistic sharing solves the problem of costly punishment. New J. Phys. 16, 083016 (2014).
Chen, X., Szolnoki, A. & Perc, M. Competition and cooperation among different punishing strategies in the spatial public goods game. Phys. Rev. E 92, 012819 (2015).
Szolnoki, A. & Perc, M. Effectiveness of conditional punishment for the evolution of public cooperation. J. Theor. Biol. 325, 34–41 (2013).
Szolnoki, A. & Perc, M. Antisocial pool rewarding does not deter public cooperation. Proc. R. Soc. B 282, 20151975 (2015)
Chen, X. J. & Perc, M. Optimal distribution of incentives for public cooperation in heterogeneous interaction environments. Front. Behav. Neurosci. 8, 248 (2014).
Szolnoki, A. & Perc, M. Correlation of positive and negative reciprocity fails to confer an evolutionary advantage: Phase transitions to elementary strategies. Phys. Rev. X 3, 041021 (2013).
Chen, X., Sasaki, T., Brännström, Å. & Dieckmann, U. First carrot, then stick: how the adaptive hybridization of incentives promotes cooperation. J. R. Soc. Interface 12, 20140935 (2015).
Perc, M., Gómez-Gardeñes, J., Szolnoki, A., Floría, L. M. & Moreno, Y. Evolutionary dynamics of group interactions on structured populations: a review. J. R. Soc. Interface 10, 20120997 (2013).
Wang, Z., Wang, L., Szolnoki, A. & Perc, M. Evolutionary games on multilayer networks: a colloquium. Eur. Phys. J. B 88, 124 (2015).
Wang, Z., Kokubo, S., Jusup, M. & Tanimoto, J. Universal scaling for the dilemma strength in evolutionary games. Phys. Life Rev. 14, 1–30 (2015).
Gürerk, Ö., Irlenbusch, B. & Rockenbach, B. The competitive advantage of sanctioning institutions. Science 312, 108–111 (2006).
Zhang, H. & Perc, M. Evolution of conditional cooperation under multilevel selection. Sci. Rep. 6 (2016).
Rockenbach, B. & Milinski, M. The efficient interaction of indirect reciprocity and costly punishment. Nature 444, 718–723 (2006).
dos Santos, M. & Wedekind, C. Reputation based on punishment rather than generosity allows for evolution of cooperation in sizable groups. Evol. Hum. Behav. 36(1), 59–64 (2015).
Boyd, R., Gintis, H., Bowles, S. & Richerson, P. J. The evolution of altruistic punishment. Proc. Natl. Acad. Sci. 100, 3531–3535 (2003).
Henrich, J. Cultural group selection, coevolutionary processes and large-scale cooperation. J. Econ. Behav. Organ. 53, 3–35 (2004).
Johnson, D. & Bering, J. Hand of god, mind of man: punishment and cognition in the evolution of cooperation. Evol. Psych. 4, 219–233 (2006).
Laurin, K., Shariff, A. F., Henrich J. & Kay, A. C. Outsourcing punishment to God: beliefs in divine control reduce earthly punishment. Proc. R. Soc. B 279, 3272–3281 (2012).
Hauert, C., Traulsen, A., Brandt, H., Nowak, M. A. & Sigmund, K. Via freedom to coercion: the emergence of costly punishment. Science 316, 1905–1907 (2007).
Sigmund, K., Silva, H. D., Traulsen, A. & Hauert, C. Social learning promotes institutions for governing the commons. Nature 466, 861–863 (2010).
Kiyonari, T. & Barclay, P. Cooperation in social dilemmas: Free riding may be thwarted by second-order reward rather than by punishment. J. Pers. Soc. Psychol. 95, 826–842 (2008).
Ye, H., Tan, F., Ding, M., Jia, Y. M. & Chen, Y. F. Sympathy and Punishment: Evolution of Cooperation in Public Goods Game. J. Artif. Soc. S. 14(4), 20 (2011).
Schoenmakers, S., Hilbe, C., Blasius, B. & Traulsen, A. Sanctions as honest signals–The evolution of pool punishment by public sanctioning institutions. J. Theor. Biol. 356, 36–46 (2014).
Boyd, R., Gintis, H. & Bowles, S. Coordinated punishment of defectors sustains cooperation and can proliferate when rare. Science 328, 617–620 (2010).
Jaffe, K. & Zaballa, L. Co-operative punishment cements social cohesion. J. Artif. Soc. S. 13 (3), 4 (2010).
Boyd, R. & Mathew, S. A narrow road to cooperation. Science 316, 1858–1859 (2007).
Mathew, S. & Boyd, R. When does optional participation allow the evolution of cooperation? Proc. R. Soc. B. 276, 1167–1174 (2009).
Schmitt, D. & Pilcher, J. J. Evaluating evidence of psychological adaptation: how do we know one when we see one? Psychol. Sci. 15, 643–649 (2004).
Suddendorf, T. Foresight and evolution of the human mind. Science 312, 1006–1007 (2006).
Cobb, C. W. & Douglas, P. H. A theory of production. Am. Econ. Rev. 18(1), 139–165 (1928).
Douglas, P. H. The Cobb-Douglas production function once again: its history, its testing, and some new empirical values. J. Polit. Econ. 84(5), 903–916 (1976).
Moran, P. The statistical processes of evolutionary theory 56–57 (Oxford Press, 1962).
Nowak, M. A., Sasaki, A., Taylor, C. & Fudenberg, D. Emergence of cooperation and evolutionary stability in finite populations. Nature 428, 646–650 (2004).
Taylor, C., Fudenberg, D., Sasaki, A. & Nowak, M. A. Evolutionary game dynamics in finite populations. B. Math. Bio. 66, 1621–1644 (2004).
Nowak, M. A. Evolutionary dynamics: exploring the equations of life 34–35 (Harvard University Press, 2006).
Metropolis, N. & Ulam, S. The monte carlo method. J. Am. Stat. Assoc. 44(247), 335–341 (1949).
Caflisch, R. E. Monte carlo and quasi-monte carlo methods. Acta Numerica. 7, 1–49 (Cambridge University Press, 1998).
Traulsen, A., Shoresh, N. & Nowak, M. A. Analytical results for individual and group selection of any intensity. B. Math. Bio. 70, 1410–1424 (2008).
Acknowledgements
This work was financially supported by the grants from the Major Project of National Social Science Foundation of China (15ZDB134), National Social Science Foundation of China (13AZD061) and National Natural Science Foundation of China (71403242).
Author information
Authors and Affiliations
Contributions
H.Y. and F.T. designed the model; H.Y., S.C. and Y.C. performed the model calculation and simulation work; J.L., Y.J. and Y.C. analysed the data and wrote the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Ye, H., Chen, S., Luo, J. et al. Increasing returns to scale: The solution to the second-order social dilemma. Sci Rep 6, 31927 (2016). https://doi.org/10.1038/srep31927
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep31927
This article is cited by
-
Cooperation dynamics in spatial public goods games with graded punishment mechanism
Nonlinear Dynamics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.