Abstract
Random lasers have been recently exploited as a photonic platform for studies of complex systems. This cross-disciplinary approach opened up new important avenues for the understanding of random-laser behavior, including Lévy-type distributions of strong intensity fluctuations and phase transitions to a photonic spin-glass phase. In this work, we employ the Nd:YBO random laser system to unveil, from a single set of measurements, the physical origin of the complex correspondence between the Lévy fluctuation regime and the replica-symmetry-breaking transition to the spin-glass phase. A novel unexpected finding is also reported: the trend to suppress the spin-glass behavior for high excitation pulse energies. The present description from first principles of this correspondence unfolds new possibilities to characterize other random lasers, such as random fiber lasers, nanolasers and small lasers, which include plasmonic-based, photonic-crystal and bio-derived nanodevices. The statistical nature of the emission provided by random lasers can also impact on their prominent use as sources for speckle-free laser imaging, which nowadays represents one of the most promising applications of random lasers, with expected progress even in cancer research.
Similar content being viewed by others
Introduction
Random lasers1,2,3 (RLs) are a special class of lasers with Lévy-type distributions of intensity fluctuations4,5,6,7,8,9,10,11,12,13, which has been recently exploited as a photonic platform for studies of complex systems, such as spin glasses14,15,16,17,18,19,20,21,22. RLs were originally proposed23 by Letokhov in the late 1960’s, but their first unambiguous observation was only reported in 1994 by Lawandy and collaborators24. Over the last two decades, studies in RLs have grown fantastically, including investigations on a myriad of interdisciplinary systems, from cold-atoms RLs25 and biomaterials26 to speckle-free laser imaging27 and cancer diagnostic28,29.
In a RL system the gain medium, which can be independent of the scatterer or simultaneously gain and scatterer, provides the optical amplification. If the gain medium is independent, the scattering nanoparticles with random spatial distribution are responsible for the necessary optical feedback1,2,3. The external cavity typical of conventional lasers is therefore not required. RL emission has been analyzed in terms of the optical modes and has been regarded as highly multimode30, in which the spectral signature can indicate that such modes are averaged out leading to a smooth spectrum, or can indicate the presence of several modes through narrowband spikes appearing after the threshold is reached31.
In this work, we demonstrate both theoretically and experimentally the correspondence between the spin-glass behavior of RLs and the Lévy flight statistics of intensity fluctuations. In the photonic context, the term spin glass (SG) means that intensity spectra emitted under identical experimental conditions keep a complex pattern of correlations15,16,17,18,19,20,21,22, as quantified below. Moreover, the Lévy statistics implies strong fluctuations in the emission intensity, with non-Gaussian heavy-tailed distribution4,5,6,7,8,9,10,11,12,13.
In ref. 19 a replica-symmetry-breaking (RSB) transition to the SG phase was experimentally reported for the first time in a RL employing a functionalized thiophene-based oligomer (T5OCx) in amorphous solid state with planar geometry. RL emission was obtained by pumping with a frequency doubled pulsed Nd:YAG laser (10 Hz, 6 ns, 1.06 μm). The RL spectrum with several spikes could be interpreted as depicting the modes riding on a broad pedestal around 610 nm, as observed when high-resolution spectral measurements were employed. When a lower spectral resolution was employed, a somewhat smooth spectrum was measured. The authors analyzed the shot-to-shot intensity fluctuations in order to obtain the RSB signature and clearly demonstrated the photonic paramagnetic to SG phase transition.
Here, we advance on the understanding and characterization of the photonic behaviors of RLs by reporting on a remarkable match between the Lévy regime of intensity emission and the critical region of the RSB glassy transition. The experimental results were obtained from a single spectral set of data on the Nd:YBO RL system. Our work thus improves on the clarification of the underlying mechanisms of the fluctuation regimes and photonic phases, which are key factors to the progress of the multiple interdisciplinary applications of RLs1,2,3.
Theoretical Framework
The complex correspondence between the RSB transition to the photonic SG phase and the changes in the statistics of intensity fluctuations in RLs can be explained within the same framework.
We start by reviewing the theoretical ground for the variety of photonic behaviors displayed by RL systems. In a series of remarkable articles15,16,17,18,19,20,21,22, a phase diagram for lasers in random amplifying media has been recently built based on the Langevin equations for the complex slow-amplitude modes ak(t),

where Fk is a Gaussian (white) uncorrelated noise term and the general complex-valued functional  reads (following closely the notation of)21
reads (following closely the notation of)21

The symbol {…}′ implies the frequency-matching conditions  and
and  in the quadratic and quartic terms, respectively, with γ denoting the finite linewidth of the modes. The physical origin of the quadratic coupling
in the quadratic and quartic terms, respectively, with γ denoting the finite linewidth of the modes. The physical origin of the quadratic coupling  lies in the spatially inhomogeneous refractive index, as well as in a nonuniform distribution of the gain and an effective damping contribution due to the “cavity” leakage. In systems with null or weak leakage in which the off-diagonal contribution is negligible, the real part of the diagonal coupling accounts for the coefficient rates of the amplification (gain) (γk) and radiation loss (αk) through
lies in the spatially inhomogeneous refractive index, as well as in a nonuniform distribution of the gain and an effective damping contribution due to the “cavity” leakage. In systems with null or weak leakage in which the off-diagonal contribution is negligible, the real part of the diagonal coupling accounts for the coefficient rates of the amplification (gain) (γk) and radiation loss (αk) through  . On the other hand, the quartic coupling
. On the other hand, the quartic coupling  is related to a modulation of the nonlinear χ(3) susceptibility with a random spatial profile15,16,17,18,19,20,21,22.
is related to a modulation of the nonlinear χ(3) susceptibility with a random spatial profile15,16,17,18,19,20,21,22.
The spatial disorder generally makes the explicit calculation of the quadratic and quartic couplings in equation (2) rather difficult. In fact, in refs 15, 16, 17, 18, 19, 20, 21, 22 these couplings have been considered as quenched Gaussian variables, with probability distributions independent of the mode combinations {k1, k2}′ and {k1, k2, k3, k4}′, respectively. In a mean-field approach15,16,17,18,19,20,21,22, all modes are coupled and the frequency-matching restrictions are relaxed. In addition, by considering the total optical intensity,  , as a constant, with time-independent prefactors ck, the real part
, as a constant, with time-independent prefactors ck, the real part  of the functional (2) becomes21,22 analogue to the Hamiltonian of the p-spin model with spherical constraint32, which is given by a sum of quadratic (p = 2) and quartic (p = 4) terms with Gaussian-distributed couplings. It is important to notice that in the photonic-to-magnetic analogy the excitation (pump) energy plays the role of the inverse temperature. An equilibrium statistical physics approach, with the replica trick applied to
of the functional (2) becomes21,22 analogue to the Hamiltonian of the p-spin model with spherical constraint32, which is given by a sum of quadratic (p = 2) and quartic (p = 4) terms with Gaussian-distributed couplings. It is important to notice that in the photonic-to-magnetic analogy the excitation (pump) energy plays the role of the inverse temperature. An equilibrium statistical physics approach, with the replica trick applied to  in terms of the slow-amplitude modes ak, then led21,22 to a phase diagram for the pumping rate as a function of the disorder strength. Photonic paramagnetic, ferromagnetic, phase-locking-wave and RSB spin-glass phases have been characterized21,22, depending on the trend of the disorder to hamper the synchronous oscillation of the modes. A photonic order parameter, analogue to the Parisi order parameter in SG theory, was suitably defined (see below), so that the value at which it is maximum assumes qmax = 0 in the prelasing replica-symmetric paramagnetic regime and qmax ≠ 0 in the random-lasing RSB glassy phase. As a consequence, the RL threshold became identified with the RSB phase transition to the photonic SG phase15,16,17,18,19,20,21,22.
in terms of the slow-amplitude modes ak, then led21,22 to a phase diagram for the pumping rate as a function of the disorder strength. Photonic paramagnetic, ferromagnetic, phase-locking-wave and RSB spin-glass phases have been characterized21,22, depending on the trend of the disorder to hamper the synchronous oscillation of the modes. A photonic order parameter, analogue to the Parisi order parameter in SG theory, was suitably defined (see below), so that the value at which it is maximum assumes qmax = 0 in the prelasing replica-symmetric paramagnetic regime and qmax ≠ 0 in the random-lasing RSB glassy phase. As a consequence, the RL threshold became identified with the RSB phase transition to the photonic SG phase15,16,17,18,19,20,21,22.
We now turn to the discussion on the statistical regimes of intensity fluctuations of RL systems in disordered nonlinear media. Noteworthy, the set of Langevin equations, given by equation (1), also provides the underlying theoretical basis for such analysis. Indeed, by writing Ik = ck|ak|2, manipulation of equation (1) leads to

The restricted sum in the quartic coupling generally involves three classes of mode combinations15,33:  and
and  ,
,  and
and  and the remaining possibilities satisfying the frequency-matching condition, which have been usually disregarded15,33. We consider the diagonal contribution in the quadratic coupling to dominate over the off-diagonal part. By expressing the optical noise as the sum of additive and multiplicative statistically independent stochastic processes34, so that
and the remaining possibilities satisfying the frequency-matching condition, which have been usually disregarded15,33. We consider the diagonal contribution in the quadratic coupling to dominate over the off-diagonal part. By expressing the optical noise as the sum of additive and multiplicative statistically independent stochastic processes34, so that  and considering slow-amplitude modes ak(t) (if compared to the rapidly evolving phase dynamics), we obtain the Fokker-Planck equation13,34 for the probability density function (PDF) of emission intensity
and considering slow-amplitude modes ak(t) (if compared to the rapidly evolving phase dynamics), we obtain the Fokker-Planck equation13,34 for the probability density function (PDF) of emission intensity

where the parameter Q controls the magnitude of the multiplicative fluctuations through 
 ,
,  , and
, and

We notice that, by averaging out the rapidly evolving phases to obtain equation (4), the so-called free running approximation has been employed in which the dynamics of the phases and amplitudes are considered as eventually decoupled15. In this context, some features of the original model are removed, such as the phase-locking regime20,21,22. Also, in a statistical physics approach we observe that integrating out irrelevant degrees of freedom should be properly done in the partition function, rather than in the Hamiltonian level, though the technical difficulties involved are rather challenging. The steady-state solution of equation (4) is13,34

with Ik > 0, Ak as the normalization constant and the power-law exponent μk = 1 + dk/2Q.
At this point we remark that, as the statistics of the sum of N independent random variables x with power-law distribution P(x) = Ax−μ, 1 < μ < 3, is described35 by the α-stable Lévy distribution with α = μ − 1, the PDF (6) thus identifies an exponentially-truncated Lévy-like distribution of intensities for 1 < μk < 3 and 0 < α < 2. In this case, strong fluctuations in Ik emerge and the ultraslow convergence to the α = 2 Gaussian behavior due to the presence of the exponential factor in equation (6) is achieved only for a remarkably large N12,35,36. In contrast, for μk ≤ 1 or μk ≥ 3 the central limit theorem assures fast convergence to the α = 2 Gaussian statistics of weakly-fluctuating intensities. Therefore, for a given disorder strength, an increasing pumping rate (or excitation pulse energy) raises13 the value of μk and the statistics of emission intensities shifts progressively from an initial Gaussian (μk ≤ 1, α = 2), to a Lévy-like (1 < μk < 3, α = μk − 1) and to a subsequent Gaussian (μk ≥ 3, α = 2) regime.
The correspondence with the RSB glassy transition relies foremost in the recent proposals6,7,8 that assign the Lévy index α as an identifier of the RL threshold, which, as discussed, can be also determined by the parameter qmax. Indeed, the above description matches accordingly with recent results on RL systems which report on7,8,9,10,11,12: (i) a prelasing weakly-fluctuating Gaussian regime at low pump energies, corresponding in refs 15, 16, 17, 18, 19, 20, 21, 22 to the photonic paramagnetic (or even the phase-locking-wave) phase with qmax = 0; followed by (ii) an abrupt change in α at the RL threshold to the strongly-fluctuating Lévy-like regime at intermediate pump energies, signaled in15,16,17,18,19,20,21,22 by the RSB transition to the glassy regime with qmax ≠ 0; and (iii) a subsequent crossover at high pump energies to the so-called self-averaged RL regime, with qmax ≠ 0 and Gaussian statistics of emitted intensities7,8,9,10,11,12. Noticeably, this latter Gaussian regime taking place deep in the glassy RL phase has not been anticipated in refs 15, 16, 17, 18, 19, 20, 21, 22, since the scope of these works did not include the analysis of the statistics of intensity fluctuations.
Experimental Results and Discussion
The experimental investigation on the above-discussed correspondence is possible through measurements in actual RL systems of the parameter qmax, whose behavior identifies the boundary between the prelasing paramagnetic and RL glassy phases and the Lévy index α, that defines the statistics of the intensity fluctuations as being Gaussian or Lévy-type. As both phenomena arise from the same theoretical framework, we employed the same set of measurements, namely the spectral intensity fluctuations, to obtain both quantities through a proper analysis.
The RL system investigated in this work consisted of crystalline powders of Nd3+-doped YBO3 (Nd:YBO) – Nd3+ concentration: 4.0 mol%37,38,39. The nanoparticle scatterers also act as the gain media. One advantage to work with this solid-state material, in comparison with the use of colloidal systems, is that in the present case the scatterers positions do not change from shot to shot, thus allowing fairly identical experimental conditions to hold over many subsequent excitation pulses22. Using a coherent backscattering setup, the measured value of the mean-free-path of photons was much larger than the typical emission wavelength (see Methods).
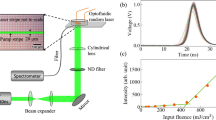
Figure 1a displays the spectral emission of the Nd:YBO system for excitation pulse energies below (1.20 mJ) and above (1.75 mJ) the RL threshold, with the latter showing the smooth signature indicating that the modes are averaged out. Even though the emitted RL spectrum is very narrow, as typical of rare-earth-doped RLs37,38,39, it does not indicate single mode operation31. In fact, it has been recently shown that even for an ultranarrow smooth spectrum, as those emitted from random Raman lasers40, the emission is multimode, as reported in41. Actually, the operation in the multimode regime is essential to the preceding theoretical analysis. The emission intensity and bandwidth narrowing are shown in Fig. 1b. With basis on the input-output measurement the estimated RL threshold is 1.36 mJ, which closely agrees with the value 1.40 mJ determined from the full width half maximum (FWHM) of the emitted spectrum. The error bar in the energy measurements is less than 7%.
Intensity spectra and the RL threshold.
(a) Spectral emission of the Nd:YBO system for two excitation pulse energies: below (green, 1.20 mJ) and above (magenta, 1.75 mJ) the RL threshold. (b) Emitted intensity (green) and bandwidth narrowing (FWHM, magenta) versus the excitation pulse energy. The intensity measure of the RL threshold implies 1.36 mJ, in close agreement with the FWHM value (1.40 mJ).
The characterization of the photonic RSB glassy transition requires the definition15,16,17,18,19,20,21,22 of an overlap parameter qγβ analogue to the Parisi overlap parameter in SG theory14. Two-point correlations can be calculated either among mode amplitudes ak20,21, phases15,16,17,18 or intensities Ik ∝ |ak|2 19,22, though the latter are the only ones accessible experimentally. In particular, by measuring fluctuations in the spectral intensity averaged over Ns shots (or system replicas; see below), the overlap parameter reads19,22.

where γ, β = 1, 2, …, Ns, with Ns = 200 at each excitation pulse energy, denote the replica labels, the average intensity at the wavelength indexed by k is  and the intensity fluctuation is given by
and the intensity fluctuation is given by  . The sum in k generally runs over 1100 values, which correspond to the discretization of the spectra in bins of 0.024 nm (see also Methods). Above the threshold, the spectra are narrowed to a FWHM around 0.20 nm, as observed in Fig. 1. In this range one has around 25 non-null values of Iγ (k) for each replica, at each excitation pulse energy. A shot of the pumping laser defines a replica, i.e. a copy of the RL system under identical experimental conditions. The PDF P (q), equivalent to the Parisi order parameter in the RSB theory of SGs, describes the distribution of replica overlaps q = qγβ, signaling a photonic uncorrelated paramagnetic or a SG phase if it peaks exclusively at q = 0 (no RSB) or also at values |q| ≠ 0 (RSB), respectively.
. The sum in k generally runs over 1100 values, which correspond to the discretization of the spectra in bins of 0.024 nm (see also Methods). Above the threshold, the spectra are narrowed to a FWHM around 0.20 nm, as observed in Fig. 1. In this range one has around 25 non-null values of Iγ (k) for each replica, at each excitation pulse energy. A shot of the pumping laser defines a replica, i.e. a copy of the RL system under identical experimental conditions. The PDF P (q), equivalent to the Parisi order parameter in the RSB theory of SGs, describes the distribution of replica overlaps q = qγβ, signaling a photonic uncorrelated paramagnetic or a SG phase if it peaks exclusively at q = 0 (no RSB) or also at values |q| ≠ 0 (RSB), respectively.
In Fig. 2a–f the pulse-to-pulse intensity fluctuations in the Nd:YBO system can be appreciated, as it evolves from the prelasing (Fig. 2a) to the RL regime (Fig. 2b–f). The corresponding plots of the PDFs P(q), shown in Fig. 2g–l, reveal a rich phase structure, emerging from the photonic paramagnetic (Fig. 2g) to the glassy RL behavior above the threshold. For excitation pulse energies below and just above the threshold (Fig. 2g–i) the photonic behavior is similar to that described in19.
Pulse-to-pulse intensity fluctuations and corresponding overlap distributions signalizing the photonic RSB glassy transition.
(a–f) Intensity spectra showing the fluctuations from shot to shot of the Nd:YBO system for excitation pulse energies (a) 1.20 mJ (below the RL threshold), (b) 1.36 mJ, (c) 1.4 mJ (both around the threshold), (d) 1.60 mJ, (e) 2.20 mJ and (f) 2.80 mJ (above the threshold). (g–l) PDF distributions of the overlap parameter corresponding to the data in Fig. 2a–f. Fluctuations are stronger (Lévy-type) close to the threshold, in the critical region of the RSB transition from the prelasing paramagnetic to the saturated RL glassy behavior. As the excitation pulse energy increases well above the threshold, fluctuations decline considerably (Gaussian regime) and the SG behavior tends to be suppressed.
For excitation pulse energies well above the RL threshold, the PDF P(q) starts to broaden (Fig. 2j–l). This is the first report of such behavior, which is related to the deep entry into the Gaussian statistical regime of intensity emission, as discussed below.
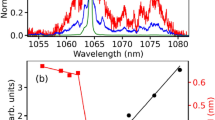
The value |q| = qmax at which the distribution P(q) assumes its maximum is related to the Edward-Anderson order parameter in SG theory14,19,22. Its behavior for the Nd:YBO system is displayed in Fig. 3a, indicating the low-energy prelasing paramagnetic (qmax ≈ 0), saturated RL SG (qmax ≈ 1) and high-energy unsaturated RL SG  regimes. Differently from the results reported in19, however, the behavior of qmax does not remain nearly constant at the saturation value qmax ≈ 1, but starts to roll over at high energies, consistently with Fig. 2. Indeed, as seen in Fig. 2e,f, well above the threshold the fluctuations of intensities decline considerably, leading to a decrease in the deviations from the pulse-to-pulse average. Correlations among intensity fluctuations also reduce, causing qmax to decay.
regimes. Differently from the results reported in19, however, the behavior of qmax does not remain nearly constant at the saturation value qmax ≈ 1, but starts to roll over at high energies, consistently with Fig. 2. Indeed, as seen in Fig. 2e,f, well above the threshold the fluctuations of intensities decline considerably, leading to a decrease in the deviations from the pulse-to-pulse average. Correlations among intensity fluctuations also reduce, causing qmax to decay.
Lévy statistics of intensity emission and the RSB glassy transition.
Dependence on the excitation pulse energy of (a) the value qmax at which the Parisi overlap order parameter assumes its maximum and (b) the Lévy index α calculated from the data in Fig. 2 of the Nd:YBO system. The regime of Lévy statistics (0 < α < 2) coincides with the critical region of the RSB transition to the RL glassy behavior. The value α = 2 identifies the Gaussian regimes below and above the transition. Notice that well above the threshold the SG behavior tends to be suppressed as qmax decreases.
The above results on the photonic behavior of the Nd:YBO system find an interrelated counterpart in the statistical properties of intensity fluctuations. By analyzing the data in Fig. 2a–f using the quantile-based McCulloch method8,42, the PDFs of intensities were identified with the family of α-stable Lévy distributions, with Lévy index α ∈ (0, 2] and boundary value α = 2 corresponding to the Gaussian behavior, according to the preceding discussion. By comparing Fig. 3a,b, it is a remarkable fact that, after shifting from the prelasing Gaussian (α = 2) statistics, the Lévy (0 < α < 2) regime corresponds to the narrow critical region of the RSB transition from the photonic paramagnetic (qmax ≈ 1) to the saturated SG RL (qmax ≈ 1) behavior. Actually, due to the sharp bandwidth narrowing around the threshold, the variation in α near the transition is also very acute. Moreover, as the excitation pulse energy increases further a subsequent α = 2 Gaussian RL regime sets in, with a trend to suppress the photonic SG phase. Indeed, in this deep Gaussian regime the system presents a considerable weakening of the intensity fluctuations, which also become less correlated as indicated by the decrease in qmax. The existence of a strict causal link between the self-averaged Gaussian regime of intensity fluctuations above the threshold and the observed trend to suppress the glassy phase should be the subject of further studies.
Overall, we remark that the experimental findings on the Nd:YBO system, displayed in Figs 2 and 3, corroborate the preceding theoretical discussion on the correspondence between the photonic RSB glassy transition and the statistics of intensity fluctuations in RLs.
In conclusion, we have analyzed both theoretically and experimentally the physical origin of the complex correspondence between the Lévy flight statistics of intensity emission and the photonic RSB glassy transition in RLs. The experimental demonstration from a single set of spectral measurements on the Nd:YBO RL system indicated a remarkable connection between the behaviors of the Lévy index and the parameter at which the equivalent of the Parisi order parameter is maximum, as a function of the excitation pulse energy. In particular, the Lévy statistical regime of intensities sets in at the RL threshold concurrently with the RSB transition from the photonic paramagnetic to SG behavior. Our results opens up new possibilities to characterize other RLs such as random fiber lasers43, nanolasers and small lasers, including plasmonic-based, photonic-crystal and bio-derived nanodevices44. Moreover, the statistical nature of the emission provided by RLs can also have impact on their use as sources for speckle-free laser imaging27, which is one of the most promising RL applications that can benefit even cancer research28,29. Finally, these practical aspects are much strengthened by the recent account45 showing that the directionality degree of RLs raises to its peak value precisely within the Lévy statistical regime.
Methods
Neodymium crystalline powder: preparation and characterization
The random laser system used in this work consisted of crystalline powders of Nd3+ doped YBO3 (Nd:YBO) obtained by the polymeric precursor method using citric acid (C5O7H8 Sigma-Aldrich) as a complexing agent, d-sorbitol (C6O6H14, Sigma-Aldrich 98%) as a polymerizing agent and yttrium nitrate hexahydrate (Y(NO3)3.6H2O, Sigma-Aldrich 99.8%), neodymium hexahydrate (Nd(NO3)3.6H2O, Sigma-Aldrich 99.8%) and boric acid (H3BO3, Ecibra 99.5%) as precursors for Y, Nd and B, respectively.
The synthesis of the material was achieved by dissolving the yttrium and neodymium nitrates in an aqueous solution of citric acid at room temperature. This solution was added to another solution of d-sorbitol and boric acid previously dissolved in water. The obtained solution was then annealed at 150 °C, whereby the polymerization process occurred, forming a dried resin.The molar ratio of citric acid to elements (metals + boron) was 3:1.The citric acid/d-sorbitol mass ratio was set to 3:2. The dried resin was calcinated at 400 °C during 24 h and heat-treated at 900 °C/1 h.
The X-ray diffraction (XRD) measurements were taken with a Shimadzu XRD-6000 X-ray diffractometer with Bragg-Brentano theta-2 theta geometry, at a continuous scan speed of 1°/min, from 5° to 80° with sampling pitch of 0.01°. K α radiation of 1.54059 Å from a Cu tube operating at 40 kV was used. The XRD pattern revealed that the YBO3 phase is an hexagonal structure with P63/mmc (194) space group and centro-symmetric.
The samples were characterized structurally using a JEOL JEM 2010 high-resolution transmission electron microscope (HRTEM) operating at 200 keV. TEM, HRTEM and SAED (selected area of electron diffraction) images of the sample displayed well-crystallized nanoparticles with oval and spherical shaped grains. The sizes distribution obtained by measuring 268 particles depicted particles ranging from 40 to 1000 nm, with the highest occurrence lying around 120 nm.
Determination of the mean-free-path
For the particle size with the highest occurrence, the scattering mean-free-path,  , defined as the average distance traversed by a photon between successive scattering events, was measured by a coherent backscattering experiment at 532 nm, using an experimental setup with a cw laser similar to those of refs 46,47.
, defined as the average distance traversed by a photon between successive scattering events, was measured by a coherent backscattering experiment at 532 nm, using an experimental setup with a cw laser similar to those of refs 46,47.
For the 4.0% Nd:YBO system, the value  was inferred. In a previous study48, the dependence on the particle size of the transport mean-free-path,
was inferred. In a previous study48, the dependence on the particle size of the transport mean-free-path,  , which gives the average distance traversed by photons before changing direction, was measured and calculated (see also ref. 49). For particle sizes around 120 nm, the estimates for
, which gives the average distance traversed by photons before changing direction, was measured and calculated (see also ref. 49). For particle sizes around 120 nm, the estimates for  , which is close to
, which is close to  , lie in the ranges 5–10 μm and 50–80 μm, at 532 nm and 1056 nm, respectively. Therefore, in either cases the transport mean-free-path is much larger than the typical emission wavelength.
, lie in the ranges 5–10 μm and 50–80 μm, at 532 nm and 1056 nm, respectively. Therefore, in either cases the transport mean-free-path is much larger than the typical emission wavelength.
Optical experiments
The optical experiments were conducted with the powder excited by an Optical Parametric Oscillator (OPO) pumped by the second-harmonic of a Q-switched Nd:YAG laser (7 ns, 10 Hz). The powder was placed on a sample holder and gently pressed into a uniform disc region. The light beam from the OPO was focused on the sample by a 10 cm focal length lens. The illuminated area was 1.8 mm2. The excitation wavelength, 806 nm, in resonance with the 4I9/2 → 4F5/2 transition, was chosen to optimize the fluorescence signal around 1060 nm due to the 4F3/2 → 4I11/2 transition, leading to a RL emission peaking at 1056 nm. The spectra were acquired with a high-resolution spectrometer coupled with a charge-coupled device (CCD), covering, in real time, the range from 1044.563 to 1070.974 nm. In the discretization of the spectra the bin width was 0.024 nm, a value that corresponds to the resolution of the acquisition system.
Although the results presented in the main text refer to the 4.0% Nd3+ concentration, we remark that samples with 0.5%, 1.0%, 1.5% and 2.0% were also studied and, except for the 0.5% and 1.0% concentrations in which RL emission was not observed, the other two samples behaved qualitatively in the same way as the 4.0% sample.
Additional Information
How to cite this article: Gomes, A. S. L. et al. Observation of Lévy distribution and replica symmetry breaking in random lasers from a single set of measurements. Sci. Rep. 6, 27987; doi: 10.1038/srep27987 (2016).
References
Luan, F. et al. Lasing in nanocomposite random media. NanoToday 10, 168–192 (2015).
Cao, H. Review on latest developments in random lasers with coherent feedback. J. Phys. A 38, 10497–10535 (2005).
Wiersma, D. S. Disordered photonics. Nature Photon. 7, 188–196 (2013).
Anglos, D. et al. Random laser action in organic-inorganic nanocomposites. J. Opt. Soc. Am. B 21, 208–213 (2004).
Sharma, D., Ramachandran, H. & Kumar, N. Lévy statistics of emission from a novel random amplifying medium: an optical realization of the Arrhenius cascade. Opt. Lett. 31, 1806–1808 (2006).
Lepri, S., Cavalieri, S., Oppo, G.-L. & Wiersma, D. S. Statistical regimes of random laser fluctuations. Phys. Rev. A 75, 063820/1–7 (2007).
Ignesti, E. et al. Experimental and theoretical investigation of statistical regimes in random laser emission. Phys. Rev. A 88, 033820/1–7 (2013).
Uppu, R. & Mujumdar, S. Lévy exponents as universal identifiers of threshold and criticality in random lasers. Phys. Rev. A 90, 025801/1–5 (2014).
Uppu, R. & Mujumdar, S. On the coherent modes of ultranarrowband random lasers with nonresonant feedback. Appl. Opt. 50, E13–E19 (2011).
Uppu, R., Tiwari, A. K. & Mujumdar, S. Identification of statistical regimes and crossovers in coherent random laser emission. Opt. Lett. 37, 662–664 (2012).
Uppu, R. & Mujumdar, S. Dependence of the Gaussian-Lévy transition on the disorder strength in random lasers. Phys. Rev. A 87, 013822/1–8 (2013).
Uppu, R. & Mujumdar, S. Exponentially tempered Lévy sums in random lasers. Phys. Rev. Lett. 114, 183903/1–5 (2015).
Raposo, E. P. & Gomes, A. S. L. Analytical solution for the Lévy-like steady-state distribution of intensities in random lasers. Phys. Rev. A 91, 043827/1–6 (2015).
Mézard, M., Parisi, G. & Virasoro, M. A. Spin Glass Theory and Beyond (World Scientific, 1987).
Angelani, L., Conti, C., Ruocco, G. & Zamponi, Z. Glassy behavior of light in random lasers. Phys. Rev. B 74, 104207/1–16 (2006).
Angelani, L., Conti, C., Ruocco, G. & Zamponi, F. Glassy behavior of light. Phys. Rev. Lett. 96, 065702/1–4 (2006).
Leuzzi, L. et al. Phase diagram and complexity of mode-locked lasers: from order to disorder. Phys. Rev. Lett. 102, 083901/1–4 (2009).
Conti, C. & Leuzzi, L. Complexity of waves in nonlinear disordered media. Phys. Rev. B 83, 134204/1–19 (2011).
Ghofraniha, N. et al. Experimental evidence of replica symmetry breaking in random lasers. Nature Commun. 6, 7058/1–7 (2015).
Antenucci, F., Conti, C., Crisanti, A. & Leuzzi, L. General phase diagram of multimodal ordered and disordered lasers in closed and open cavities. Phys. Rev. Lett. 114, 043901/1–5 (2015).
Antenucci, F., Crisanti, A. & Leuzzi, L. Complex spherical 2 + 4 spin glass: a model for nonlinear optics in random media. Phys. Rev. A 91, 053816/1–24 (2015).
Antenucci, F., Crisanti, A. & Leuzzi, L. The glassy random laser: replica symmetry breaking in the intensity fluctuations of emission spectra. Sci. Rep. 5, 16792/1–11 (2015).
Letokhov, V. S. Generation of light by a scattering medium with negative resonance absorption. Sov. J. Exp. Theor. Phys. 26, 835–840 (1968).
Lawandy, N. M., Balachandran, R. M., Gomes, A. S. L. & Sauvain, E. Laser action in strongly scattering media. Nature 368, 436–438 (1994).
Baudouin, Q. et al. A cold-atom random laser. Nature Phys. 9, 357–360 (2013).
Zhang, D., Kostovski, G., Karnutsch, C. & Mitchell, A. Random lasing from dye doped polymer within biological source scatters: the pomponia imperatorial cicada wing random nanostructures. Org. Electron. 13, 2342–2345 (2012).
Redding, B., Choma, M. A. & Cao, H. Speckle-free laser imaging using random laser illumination. Nature Photon. 6, 355–359 (2012).
Lahoz, F. et al. Random laser in biological tissues impregnated with a fluorescent anticancer drug. Laser Phys. Lett. 12, 045805/1–6 (2015).
Polson, R. C. & Vardeny, Z. V. Cancerous tissue mapping from random lasing emission spectra. J. Opt. 12, 024010/1–4 (2010).
Türeci, H. E., Ge, L., Rotter, S. & Stone, A. D. Strong interactions in multimode random lasers. Science 320, 643–646 (2008).
Cao, H. et al. Random laser action in semiconductor powder. Phys. Rev. Lett. 82, 2278–2281 (1999).
Crisanti, A. & Sommers, H.-J. The spherical p-spin interaction spin glass model: the statics. Z. Phys. B 87, 341–354 (1992).
O’Bryan, I. C. L. & Sargent, I. M. Theory of multimode laser operation. Phys. Rev. A 8, 3071–3092 (1973).
Schenzle, A. & Brand, H. Multiplicative stochastic processes in statistical physics. Phys. Rev. A 20, 1628–1647 (1979).
Mantegna, R. N. & Stanley, H. E. Stochastic process with ultraslow convergence to a Gaussian: the truncated Lévy flight. Phys. Rev. Lett. 73, 2946–2949 (1994).
Bartumeus, F., Raposo, E. P., Viswanathan, G. M. & da Luz, M. G. E. Stochastic optimal foraging: tuning intensive and extensive dynamics in random searches. PLoS One 9, e106373/1–11 (2014).
Moura, A. L. et al. Multi-wavelength emission through self-induced second-order wave-mixing processes from a Nd3+ doped crystalline powder random laser. Sci. Rep. 5, 13816/1–7 (2015).
Moura, A. L. et al. Random lasing in Nd3+ doped potassium gadolinium tungstate crystal powder. J. Appl. Phys. 117, 083102/1–3 (2015).
Garca-Revilla, S. et al. Random laser performance of NdxY1−xAl3(BO3)4 laser crystal powders. J. Opt. Mater. 34, 461–464 (2011).
Hokr, B. H. et al. Bright emission from a random Raman laser. Nature Commun. 5, 4356 (2014).
Hokr, B. H. et al. Evidence of Anderson localization effects in random Raman lasing. SPIE Proc. 9731, 973110/1–6, doi: 10.1117/12.2212911 (2016).
McCulloch, J. H. Simple consistent estimators of stable distribution parameters. Commun. Stat. Simul. 15, 1109–1136 (1986).
Churkin, D. V. et al. Recent advances in fundamentals and applications of random fiber lasers. Adv. Opt. Photon. 7, 516–569 (2015).
Hill, M. T. & Gather, M. C. Advances in small lasers. Nat. Photonics 8, 908–918 (2014).
Tommasi, F., Ignesti, E., Fini, L. & Cavalieri, S. Controlling directionality and the statistical regime of the random laser emission. Phys. Rev. A 91, 033820/1–7 (2015).
Corey, R., Kissner, M. & Saulnier, P. Coherent backscattering of light. Am. J. Phys. 63, 560–564 (1995).
Labeyrie, G. et al. Observation of coherent backscattering of light by cold atoms. J. Opt. B 2, 672–685 (2000).
Noginov, M. A. et al. Dependence of NdSc3(BO3)4 random laser parameters on particle size. J. Opt. Soc. Am. B 21, 191–200 (2004).
Noginov, M. A. Solid-State Random Lasers (Springer, 2005).
Acknowledgements
We thank Robin Kaiser from the Institut Non Linéaire de Nice for enlightening discussions. Work supported by the PRONEX Program, National Institute of Photonics - INFO, Conselho Nacional de Desenvolvimento Cientfico e Tecnológico (CNPq), Coordenação de Aperfeiçoamento de Pessoal de Nvel Superior (CAPES), Financiadora de Estudos e Projetos (Finep) and Fundação de Amparo à Ciência e Tecnologia do Estado de Pernambuco (FACEPE) (Brazilian agencies).
Author information
Authors and Affiliations
Contributions
A.S.L.G., E.P.R. and C.B.A. conceived and designed the study. A.S.L.G., E.P.R., A.L.M., S.I.F., P.I.R.P., L.J.Q.M. and C.B.d.A. discussed the results and wrote the manuscript. A.S.L.G., A.L.M., S.I.F., P.I.R.P., V.J., L.J.Q.M. and C.B.d.A. prepared the samples and performed the experiments. S.I.F. and P.I.R.P. analyzed the statistics of the intensity fluctuations. A.S.L.G. and E.P.R. performed the theoretical analysis.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Gomes, A., Raposo, E., Moura, A. et al. Observation of Lévy distribution and replica symmetry breaking in random lasers from a single set of measurements. Sci Rep 6, 27987 (2016). https://doi.org/10.1038/srep27987
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep27987
This article is cited by
-
Investigation of Random Laser in the Machine Learning Approach
Brazilian Journal of Physics (2024)
-
Transient replica symmetry breaking in Brillouin random fiber lasers
PhotoniX (2023)
-
Random lasing and replica symmetry breaking in GeO2-PbO-MgO glass–ceramics doped with neodymium
Scientific Reports (2022)
-
Simultaneous evaluation of intermittency effects, replica symmetry breaking and modes dynamics correlations in a Nd:YAG random laser
Scientific Reports (2022)
-
LSFQPSO: quantum particle swarm optimization with optimal guided Lévy flight and straight flight for solving optimization problems
Engineering with Computers (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.