Introduction

Strongly correlated electron systems show many interesting and important properties such as high Tc superconductivity, colossal magnetoresistive effect, multi-ferroics, and giant thermoelectric conversion. These properties appear in or in the vicinity of the Mott insulating state in which some of the degrees of freedom associated with the electron are ordered, and these are commonly believed to be driven by the strong Coulomb interaction. In these systems, enhanced fluctuations of spin, charge, and orbital correlations in the proximity of the ordered states play an important role for the attractive properties mentioned above. Therefore, spin fluctuations in the energy-momentum space are widely studied by inelastic neutron scattering1,2,3,4. Recently, resonant inelastic x-ray scattering (RIXS) at the transition metal L-edge has become a complementary technique in measuring spin-flip magnetic excitations5,6. In contrast, charge fluctuations have hardly been explored in the energy- and momentum-resolved fashion so far because of the limitation of experimental methods. In principle, inelastic scattering of photons or electrons is directly connected to dynamical charge correlation, but these techniques have shortcomings: nonresonant inelastic x-ray scattering usually suffers from low cross-section, and inelastic electron scattering (electron energy loss spectroscopy, EELS) presents difficulties in sample preparation and interpretation due to multiple scattering. Under these circumstances, RIXS at the transition metal K-edge, which is referred to as indirect RIXS7, is a possible candidate for observing charge fluctuations because resonant enhancement facilitates the observation of charge excitations within a realistic time frame. Up till now, it has been demonstrated that K-edge RIXS spectra are qualitatively similar to the dynamical charge correlation function N( q , ω)8, and the cross-section of K-edge RIXS is represented by N( q , ω) under a certain approximation9,10.

We apply the K-edge RIXS technique to two systems that show a charge order and observe the momentum-resolved charge fluctuations proximate to the charge-ordered phase in strongly correlated transition metal oxides. One is Sr14−xCaxCu24O41, which is a composite crystal consisting of a two-leg ladder and an edge-shared chain with different periodicity. The ladder part with a large transfer energy of carriers is responsible for most physical properties. Isovalent substitution of Ca for Sr causes transfer of holes from the chain to the ladder11,12, and superconductivity at large Ca concentrations under high pressure has attracted great interest13,14. The nominal valence of Cu is +2.25, and holes are already doped in the ladder in parent Sr14Cu24O41. The charge-order formation at x = 0 was established from impedance measurements15,16, and a resonant elastic x-ray scattering study confirmed a five-fold periodicity of the charge order17. When additional holes are doped into the ladder by partially substituting Ca for Sr, the order melts suddenly18. The other system is the triangular bilayer in LuFe2O4, in which equal amounts of Fe2+ and Fe3+ coexist. A three-fold charge order is realized in LuFe2O419, but the charge is situated on a frustrated geometry in contrast to the two-leg ladder in Sr14−xCaxCu24O41. It has been theoretically argued that the frustration leads to the formation of a novel 3-fold charge order with electric polarization20. Note that a recent structural analysis proposed a nonpolar charge arrangement within the bilayer in contrast to the previously believed polar bilayer21. Nevertheless, the geometrical charge frustration and the three-fold charge order, which are the two important features in the present study, are maintained.

In the present study, we observe the charge fluctuations in the momentum-energy space induced by thermal or quantum melting of the charge order of strongly correlated electrons. These fluctuations appear as a continuum spectral weight in RIXS spectra and show characteristic momentum dependence: the spectral weight is enhanced only at the propagation vector of the charge order ( qCO) in the two-leg ladder lattice, whereas it is observed at some momentum points in the triangular bilayer lattice. The latter case is analogous to geometrical spin frustration, namely competition among various charge configurations emerges as charge fluctuations which spread across the wide momentum space.

Results

Excitations in the two-leg ladder lattice

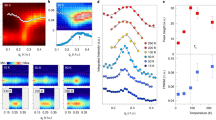
We begin with the two-leg ladder lattice in Sr14−xCaxCu24O41. Figure 1a shows Cu K-edge RIXS spectra of the parent Sr14Cu24O41 below (8 K) and above (400 K) the charge-order transition temperature TCO ≈ 250 K. Because the momentum dependence perpendicular to the ladder plane is weak, we discuss the reduced momentum in the ladder plane represented as q = (qrung, qleg). The intense signal above 2 eV is ascribed to a charge-transfer excitation from the Zhang-Rice band to the upper Hubbard band of the ladder22. It is already observed in an undoped Mott insulating compound. When holes are doped, continuum-like weight appears below the charge-transfer gap and its intensity is proportional to the hole concentration22. This spectral weight originates from intraband excitations, namely dynamical response of the doped holes in the ladder. Because the charge order in Sr14Cu24O41 is regarded as a spatial modulation of the doped holes, we can directly investigate the dynamics of doped holes from the intraband excitations around 1 eV. Therefore variation of the spectral weight of the intraband excitations is the main subject of this study.

Figure 1: Charge excitations in the two-leg ladder lattice in Sr14−xCaxCu24O41.
figure 1

(a,d,f) Raw RIXS spectra of x = 0, 3 and 6 measured at 8 K and 400 K. (b,e,g) Momentum dependence of integrated spectral weight at 1.0–1.4 eV. The vertical thick bars denote the propagation vector of the charge order at x = 0 ( qCO). (c) Temperature dependence of integrated spectral weight at 1.0–1.4 eV. Intensity of resonant elastic x-ray scattering (RXS) taken from ref. 17 is also presented. The vertical thick bar shows the transition temperature of the charge order (TCO). (h) Enhancement of the RIXS intensity at qCO. The definition is given in the main text. The thick solid lines in (c,h) are a guide for eyes.

Full size image

At 8 K, the momentum dependence of the intensity of the continuum-like spectral weight is weak. Figure 1a shows that it is slightly higher at q = (0, 0.2) than at the other two momenta, i.e., q = (0, 0) and (0, 0.5). When the charge order is thermally melted at 400 K, the momentum dependence changes considerably; the intensity is enhanced substantially at q = (0, 0.2), which coincides with the propagation vector of the five-fold charge order ( qCO). The momentum dependence of the continuum-like spectral weight is shown in Fig. 1b, where we show a plot of the integrated RIXS intensity between 1.0 and 1.4 eV after subtracting the corresponding intensity of the anti-Stokes region (between −1.4 and −1.0 eV). It is clear that the enhanced intensity at 400 K is observed just at qCO, while momentum dependence of the intensity is rather flat at lower temperatures. Figure 1c shows the temperature dependence of the integrated RIXS intensity at four momenta, two of which are the propagation vectors of the charge order qCO. We superimpose the intensity of resonant elastic x-ray scattering taken from ref. 17, which corresponds to the order parameter of the charge order evolving below the transition temperature (TCO ≈ 250 K). While the integrated RIXS intensity is constant at temperatures well below TCO, it begins to increase with increasing temperature near TCO. The marked change in temperature dependence across TCO suggests that the increase in RIXS intensity above TCO is related to the melting of the charge order. Notably, the increase is larger at qCO than at other momenta. From the result in Fig. 1b,c, we can divide the increase in RIXS spectral weight above TCO into two components. One is enhanced intensity at qCO and the other is momentum-independent part. Because of the coincidence of momentum and temperature, we reasonably ascribe the former component to the fluctuations of the melted charge order. To our knowledge, such momentum- and energy-resolved charge fluctuations proximate to the charge-ordered phase have never been observed experimentally thus far. On the other hand, one possibility to account for the latter component is the increase in the number of mobile holes associated with the charge order melting. In other words, holes are localized below TCO, which is indicated by a kink in resistivity23. Alternatively, a nuclear magnetic resonance study suggests that the number of holes in the ladder itself changes with temperature due to charge transfer between the ladder and the chain24.

In Sr14−xCaxCu24O41, the static charge order of x = 0 disappears suddenly on hole doping into the ladder by substituting Ca for Sr; this is considered quantum melting18. It is interesting to see how the charge fluctuations change with the melting. Figure 1d shows the raw RIXS spectra of x = 3 at 8 K and 400 K. Similar to the case of x = 0, enhanced intensity at qCO = (0, 0.2) is observed at 400 K, whereas the continuum intensity around 1 eV is almost independent of momentum at 8 K. In Fig. 1e, we plot the momentum dependence of the integrated RIXS intensity between 1.0 and 1.4 eV. Charge fluctuations are observed as enhancements at qCO, and they are prominent at 300 K and 400 K. When holes are doped further to x = 6, the temperature dependence of the fluctuations changes. Figure 1f,g show the raw RIXS spectra and the momentum dependence of the integrated RIXS intensity, respectively. The enhancement at qCO remains, but it is rather noticeable at lower temperatures. Slight shift of the peak from qCO at x = 6 in Fig. 1g may indicate that an increase in the number of holes in the ladder causes incommensuration, which destabilizes the static charge order. Figure 1h shows a summary of the doping dependence. The radii of the circles in the figure show the magnitude of the enhancement at qCO which is defined as , where N is the number of measured momentum points except for qCO. The radius becomes zero when no enhancement is observed at qCO. With increasing the hole concentration in the ladder, the charge fluctuations at qCO become prominent at lower temperatures, which means the dynamical charge correlation with five-fold periodicity become destabilized by hole doping.

Note that we extended the measurement of RIXS up to x = 11.5, but we could not observe the fluctuations of three-fold periodicity in the proximity of the three-fold charge ordered phase at x ~ 11, even though the three-fold static charge order was established by resonant elastic x-ray scattering18. (Detailed RIXS studies of high Ca concentrations will be published elsewhere.) These results imply that the three-fold charge order at x ~ 11 is qualitatively different from the five-fold charge order at x = 0 in the energy scale, as discussed later.

Excitations in the triangular bilayer lattice

Since we have established the capability of RIXS to measure charge fluctuations, we proceed to the more complex case of LuFe2O4, where the charge degree of freedom is geometrically frustrated in the triangular bilayer lattice. Figure 2a shows raw RIXS spectra at the Fe K-edge at temperatures well below, slightly below, and above the transition temperature of three-dimensional charge order TCO = 330 K19. The RIXS intensity at around 1 eV increases at high temperatures, except for the in-plane zone center Q = (0, 0, 19.5). Analogous to the result of Sr14−xCaxCu24O41, we ascribe the increase at around 1 eV to charge fluctuations related to the charge order. We plot the integrated RIXS intensity between 0.8 and 1.0 eV after subtracting the corresponding intensity of the anti-Stokes region (between −1.0 and −0.8 eV) in Fig. 2c,d, respectively, for Q = (h, k, 19.5) and (h, k, 21). This energy window is ascribed to the charge fluctuations between Fe2+ and Fe3+ from an optical study25. When the charge order is melted at 400 K, the charge fluctuations are enhanced. In distinct contrast to the case of the two-leg ladder, the enhancement above TCO is observed not only at (close to) the propagation vector of the charge order within the layer but also at other in-plane momenta and (1/4, 1/4). Here q denotes the reduced in-plane momentum of the triangular bilayer. Temperature dependence of the integrated RIXS intensity at 0.8–1.0 eV is shown in Fig. 2e. The intensities at both and q = (1/2, 0) begin to increase above 100 K (≪TCO), and the slope becomes steeper above TCO.

Figure 2: Charge excitations in the triangular-bilayer lattice in LuFe2O4.
figure 2

(a) Raw RIXS spectra measured at 15, 280 and 400 K. (b) Reciprocal lattice of the triangular lattice. The yellow triangle is the irreducible Brillouin zone. (c,d) Momentum dependence of integrated spectral weight at 0.8–1.0 eV. The vertical thick bars denote the in-plane propagation vector of the charge order ( qCO). Open and filled circles represent the data recorded in the 1st and 2nd experiments, respectively. The two experiments were performed independently, but the same sample was measured. (e) Temperature dependence of integrated spectral weight at 0.8–1.0 eV. The arrow indicates the transition temperature of the charge order (TCO), and the thick line is to serve as a guide for eyes.

Full size image

Theoretical calculation

To confirm the qualitative difference of charge fluctuations between systems with and without geometrical frustration, we calculated the temperature dependences of the dynamical charge correlation functions (DCCF). Correlated electron systems with and without geometrical frustration are simulated using the interacting fermion models, termed the Vt models, on the triangular bilayer and square lattices, respectively. We have confirmed in our previous papers20,26 that this model on the triangular bilayer can reproduce the CO structure in LuFe2O4. Because the charge pattern in the ladder plane of Sr14Cu24O41 has not been determined experimentally, we adopt the square lattice as a model without charge frustration. A checkerboard-type CO and polar three-fold CO appear in the square and triangular bilayer lattices, respectively, at low temperatures. The DCCFs at finite temperature are calculated numerically by applying the exact diagonalization method based on the Householder algorithm to finite-sized clusters. Low-energy charge fluctuations are deduced by integrating the excitation spectra of the DCCF up to a cut-off energy as , where N( q , ω) is the DCCF, ωc is chosen to be below the insulating gap at zero temperature, and the elastic component located at around ω = 0, corresponding to the superlattice diffraction peak, is removed.

Figure 3a,b show the temperature dependences of the integrated intensity I( q ) in the square and triangular bilayer lattices, respectively. The integrated intensities are almost zero at temperatures well below TCO in the square lattice model, implying that the static CO develops well, and begin to increase near TCO with increasing temperature. The increase in intensity near TCO is more prominent at the propagation vector of CO, qCO = (1/2, 1/2), than at other momenta. The temperature dependence of I( q ) in the triangular bilayer lattice is qualitatively contrastive. There are two characteristic temperatures, termed T6CO and T3CO (T6CO > T3CO), in which the six-fold and three-fold COs set in, respectively. The latter T3CO corresponds to the experimentally observed CO temperature at TCO = 330 K in LuFe2O4 shown in Fig. 2e. It is shown that even below T3CO, intensive low-energy charge fluctuation remains. A weak kink is confirmed at around T3CO in the temperature dependence of I( q ). These behaviors appear not only at qCO but also at (−1/2, 1/2).

Figure 3: Theoretical charge fluctuation intensities.
figure 3

(a,b) Temperature dependences of integrated dynamical charge correlation functions in square lattice and triangular bilayer lattices. TCO in (a) represents the charge-ordering temperature of checkerboard-type CO, and T3CO and T6CO, respectively, in (b) represent the charge-ordering temperatures of the three-fold and six-fold COs, corresponding to three- and two-dimensional COs in LuFe2O4. Insets show the first Brillouin zones and the momenta at which the dynamical charge correlation functions were calculated.

Full size image

When we focus on the temperature regions up to a few ten percent higher than TCO and T3CO, the momentum dependence of I( q ) in the triangular bilayer lattice is weaker than that in the square lattice. Note that the momenta (1/2, 0) and (−1/2, 1/2) are equivalent under the three-fold symmetry of the triangular bilayer lattice. These theoretical results explain well the experimental observations made for Sr14Cu24O41 and LuFe2O4.

Discussion

For both Sr14−xCaxCu24O41 and LuFe2O4, charge fluctuations are observed at of the order of 1 eV. Even though the charge fluctuations may also appear at lower energy, we emphasize here that the charge fluctuations extend to large energy scale. This suggests that the strong electron-electron interaction at the same energy scale is relevant to the charge order, and we consider that the interaction at the highest-energy scale plays a primary role in the occurrence of the charge order. Other interactions, such as magnetic and electron-phonon interactions, may contribute to the charge order to some extent. Even so, energy scale of the interactions is lower than the Coulomb interaction and their role is secondary. Importance of the strong electronic interaction has been indicated in the optical studies. In the optical conductivity of Sr14Cu24O41, spectral weight below ~1 eV is suppressed largely with decreasing temperature, and it moves toward higher energy27,28, namely spectral transfer occurs up to the order of 1 eV, which is comparable to the charge fluctuations observed in RIXS. The large energy scale in Sr14Cu24O41 accords with the argument that the charge order is considered as a sort of Wigner crystallization driven by many-body electronic effects in which a detectable lattice distortion is missing17. In contrast, the suppression of the spectral weight in optical conductivity is significant at one order lower energy (<0.1 eV) at high Ca concentration29,30, even though a three-fold charge order is established at x ~ 11 by resonant elastic x-ray scattering18. This indicates that the charge order at x ~ 11 is a phenomenon at energies lower than that at x = 0, namely charge orders are qualitatively different between x = 0 and x ~ 11.

Similarly, in LuFe2O4, the spectral weight of optical conductivity at 0.6–1.0 eV, which is ascribed to the charge fluctuations between Fe2+ and Fe3+ in the study, is suppressed below TCO 25, and the energy is comparable to that of the charge fluctuation observed in the present RIXS study. Therefore, the charge order in LuFe2O4 is also likely to be driven by the electron-electron interaction. The most important difference between Sr14Cu24O41 and LuFe2O4 is the momentum dependence of charge fluctuations. While the fluctuations are limited only at (or close to) qCO in the former, they are observed at two- [ q = (1/2, 0)], three- [ q = (1/3, 1/3)] and four- [ q = (1/4, 1/4)] periodicities in the latter. This can probably be ascribed to the geometrical charge frustration inherent in the triangular lattice. In general, difference of the free energy among various charge configurations is very small if the charge frustration exists. In the case of LuFe2O4, a theoretical calculation has demonstrated that free energies of two-, three-, and four-fold charge-ordered states are close to each other and a slight change in a parameter in the theoretical model switches the state from one to the other20,26. The three-fold charge-ordered state is realized below TCO, but, when the order is melted, competition between the states emerges as fluctuations at the finite energy.

One may concern how such charge fluctuations appear in high-Tc cuprates because the topic of charge-ordered states in underdoped regions has recently attracted great interest as a competing phenomenon to superconductivity31,32,33. Some of the present authors observed enhancement of the intraband excitations at the propagation vector of the charge order qCO in a Cu K-edge RIXS study of the charge-stripe-ordered La2−x(Ba,Sr)xCuO4 (x ~ 1/8)34. The result of the high-Tc cuprates is similar to the present study of Sr14−xCaxCu24O41 in the sense that the intraband excitations around 1 eV form a peak at qCO in the momentum space, but the enhancement is qualitatively different between the two systems. In the high-Tc cuprates, the enhancement was observed in the ordered phase and thereby collective stripe excitations and anomalous softening of the charge excitonic modes of the in-gap states are proposed as a possible origin. We note that a subsequent study of the high-Tc cuprates35 showed that the enhancement near qCO extends to the overdoped region, indicating that direct relation of the enhancement to the charge-stripe order is unlikely. In contrast, the enhancement in Sr14−xCaxCu24O41 is prominent when the order is melted in the disorderd phase, and it is less clear or missing in the ordered phase. Recently, Cu L3-edge RIXS was also applied to the study of charge-ordered cuprates. Though a superlattice peak of the charge order was observed at the elastic or quasi-elastic position in the ordered phase31,36,37 and magnetic excitations might change slightly across the qCO36,38, charge fluctuations at a finite energy have not been observed in the disorded phase so far. Observation of the charge fluctuations in the high-Tc cuprates still remains to be done. Difficulty of the observation may come from energy scale of the charge fluctuations lower that the energy resolution. Judging from the temperature dependence of optical conductivity of the stripe-ordered high-Tc cuprates39,40, charge fluctuation associated with the thermal melting of the charge order would appear at ~0.1 eV in the high-Tc cuprates. If so, observation of the charge fluctuation is a challenging subject even in the state-of-the-art RIXS spectrometer. In Sr14Cu24O41, low dimensionality of the two-leg ladder and low electric conductivity prevent carriers from screening the electron-electron interaction, which keeps the charge fluctuation at higher energies. The substitution of Ca for Sr makes the compound conductive not only along the leg but also along the rung in Sr14−xCaxCu24O41 41; consequently, the screening is effective at high Ca concentrations, as is in the high-Tc cuprates.

In the present study, we show that charge fluctuations proximate to charge order appear in the RIXS spectra of Sr14−xCaxCu24O41 and LuFe2O4. Because the charge fluctuations resolved in both energy and momentum have never been observed so far, our RIXS results unfold a new aspect of charge fluctuations in strongly correlated electron systems.

Methods

We prepared single crystals of Sr14−xCaxCu24O41 (x = 0, 3 and 6) and LuFe2O4 by the traveling solvent floating zone method. The sample surfaces normal to the two-leg ladder plane (ac-plane) and the triangular lattice plane (ab-plane), respectively, in Sr14−xCaxCu24O41 and LuFe2O4 were irradiated with x-rays.

The Cu and Fe K-edge RIXS experiments were performed at BL11XU in SPring-8. Incident x-rays were monochromatized by a Si(111) double-crystal monochromator, and the energy bandwidth was reduced further by a Si(400) channel-cut monochromator for both edges.

At the Cu K-edge, horizontally scattered x rays were analyzed in energy by a spherical Ge(733) analyzer, and the total energy resolution estimated from the full width at half maximum (FWHM) of the elastic peak was approximately 400 meV. Single crystals of Sr14−xCaxCu24O41 were mounted such that the bc-plane was parallel to the scattering plane when momentum transfer along the a*-direction was zero. Under this experimental geometry, the polarization of the incident photons ( εi) has almost equal b and c components. The b* component of momentum transfer was selected such that the scattering angle (2θ) was close to 90°. Then, absolute momentum transfers ( Q ) for x = 0, 3 and 6 were (H, 13.6, L), (H, 13.4, L) and (H, 13.2, L), respectively. Incident photon energy was fixed at 8993 eV for the RIXS measurements, the same as in a previous study22. This photon energy is slightly higher than the poorly-screened final state of the x-ray absorption of ε ‖ b , where ε denotes the photon polarization in x-ray absorption. This incident photon energy is close to the energy where a core-hole is created at a hole-doped site, and it was demonstrated that the Cu K-edge RIXS spectra agree well with the dynamical charge correlation function when the incident photon energy is tuned to the condition35,42.

In Fig. 1b,e,g, we integrated the intensity between 1.0 and 1.4 eV. More precisely, we added the intensity of three data points at 1.0, 1.2 and 1.4 eV because we measured the spectra at 0.2 eV step. In order to show how the results are robust irrespective of the integration window, we plot the intensity of each data point after subtracting the corresponding intensity of the anti-Stokes region in Supplementary Fig. S1. The enhancement at qco is still clear. Furthermore, we measured the key spectra (8 K and 400 K for x = 0, and 8 K for x = 6) twice and the second scans are shown in Supplementary Fig. S2. They are almost identical to the spectra in Fig. 1(a,f).

We used a Ge(620) analyzer for the Fe K-edge. Total energy resolution was approximately 500 meV. The horizontal scattering plane was spanned along the directions. The incident photon energy was set to 7130 eV, where excitations at a few eV were enhanced resonantly, as shown in Supplementary Fig. S3.

Theoretical calculations were performed on the interacting fermion systems modeled by the spinless fermion Vt-model Hamiltonian given by

where (ci) is the creation (annihilation) operator for a spinless Fermion at site i and is a fermion number operator. Inter-site fermion hoppings (tij) and Coulomb interactions (Vij), respectively, were considered up to the 2nd and the 3rd neighboring sites in a triangular bilayer lattice. In a square lattice, both tij and Vij were introduced between the nearest neighbor sites. The cluster mean-field method was applied to finite-sized clusters. We used the open boundary condition, in which the Coulomb interaction term (the second term in Eq. (1)) is decoupled, and introduced the mean fields 〈ni〉. The Hamiltonians of finite-sized systems were analyzed by the Householder algorithm, and the mean-fields were determined self-consistently with the states in a cluster. Cluster sizes were taken as 10 and 12 for square and triangular bilayer lattices, respectively. We calculated numerically the dynamical charge correlation function at a finite temperature defined by

where Z is the partition function, β is the inverse temperature and η is a small numerical constant.

Additional Information

How to cite this article: Yoshida, M. et al. Observation of momentum-resolved charge fluctuations proximate to the charge-order phase using resonant inelastic x-ray scattering. Sci. Rep. 6, 23611; doi: 10.1038/srep23611 (2016).