Abstract
We propose a quantum processor for the scalable quantum computation on microwave photons in distant one-dimensional superconducting resonators. It is composed of a common resonator R acting as a quantum bus and some distant resonators rj coupled to the bus in different positions assisted by superconducting quantum interferometer devices (SQUID), different from previous processors. R is coupled to one transmon qutrit and the coupling strengths between rj and R can be fully tuned by the external flux through the SQUID. To show the processor can be used to achieve universal quantum computation effectively, we present a scheme to complete the high-fidelity quantum state transfer between two distant microwave-photon resonators and another one for the high-fidelity controlled-phase gate on them. By using the technique for catching and releasing the microwave photons from resonators, our processor may play an important role in quantum communication as well.
Similar content being viewed by others
Introduction
Quantum computation1, which can implement the famous Shor’s algorithm2 for integer factorization and Grover/Long algorithm3,4 for unsorted database search, has attracted much attention in recent years. There are some interesting systems which have been used to realize quantum computation, such as photons5,6, quantum dots7,8, nuclear magnetic resonance9,10,11, diamond nitrogen-vacancy center12,13 and cavity quantum electrodynamics (QED)1. Achieving quantum computation, quantum state transfer14,15 and universal quantum gates have been studied a lot, especially the two-qubit controlled-phase (c-phase) gate or its equivalent (controlled-not gate) which can be used to construct a universal quantum computation assisted by single-qubit operations1. To construct the high-efficiency and high-fidelity quantum state transfer and the c-phase gate on fields or atoms, cavity QED, composed of a two-energy-level atom coupled to a single-mode filed, has been studied a lot.
Simulating cavity QED, circuit QED16,17,18,19,20,21,22,23,24,25,26,27, composed of a superconducting qubit coupled to a superconducting resonator, plays an important role in quantum computation because of its good ability for the large-scale integration28,29,30,31,32,33. By far, some important tasks of quantum computation based on the superconducting qubits have been realized in experiments. For example, DiCarlo et al. demonstrated a c-phase gate on two transmon qubits34 in 2009 and they prepared and measured the entanglement on three qubits in a superconducting circuit35 in 2010. In 2012, Lucero et al.36 computed the prime factors with a Josephson phase qubit quantum processor and Reed et al.37 constructed a controlled-controlled phase gate to realize a three-qubit quantum error correction with superconducting circuits. In 2014, Barends et al.38 realized the single-qubit gate and the c-phase gate on adjacent Xmon qubits with high fidelities of 99.94% and 99.4%, respectively.
Interestingly, the quality factor of a one-dimensional (1D) superconducting resonator39 has been enhanced to 106, which makes the resonator as a good carrier for quantum information processing40,41,42,43,44,45,46,47,48,49,50,51,52. For instance, Houck et al.53 generated single microwave photons in a circuit in 2007. In 2008, Hofheinz et al.54 generated the Fock states in a superconducting quantum circuit. In 2010, Johnson et al.55 realized the quantum non-demolition detection of single microwave photons in a resonator. In 2011, Wang et al.56 deterministically generated the entanglement of photons in two superconducting microwave resonators and Strauch et al.57 proposed a scheme to prepare the NOON state on two resonators. In 2013, Yang et al.58 presented two schemes for generating the entanglement between microwave photons and qubits. Recently, Hua et al.59 proposed some schemes to construct the universal c-phase and cc-phase gates on resonators.
There have been some theoretic studies on constructing the multi-resonator quantum entanglement and the universal quantum gate on local microwave-photon resonators in a processor composed of some resonators coupled to a superconducting qubit57,58,59,60,61. In this paper, we propose a quantum processor for quantum computation on distant resonators with the tunable coupling engineering62,63 between the superconducting resonator and the quantum bus. There is just one superconducting transmon qutrit q in our processor, which is coupled to a common resonator R (acts as a quantum bus). Different from the processors in previous works57,58,59,60,61, the resonators rj (j = 1, 2) (act as the information carriers) in our processor are coupled to the quantum bus R, not the qutrit, which makes it have the capability of integrating some distant resonators35 by coupling them to the bus in different positions. In contrast with the resonator-zero-qubit architecture by Galiautdinov et al.31, the resonators in our processor are used for quantum information processing, not the memory elements. It does not require more superconducting qubits. With our processor, we present an effective scheme for the quantum state transfer between r1 and r2 with the Fock states  and
and  and another for the c-phase gate on two resonators by using the resonance operations between R and rj and that between R and q. The fidelities of our quantum state transfer and c-phase gate are 99.97% and 99.66%, respectively. By catching and releasing the microwave photons from resonators64, our processor maybe play an important role in quantum communication.
and another for the c-phase gate on two resonators by using the resonance operations between R and rj and that between R and q. The fidelities of our quantum state transfer and c-phase gate are 99.97% and 99.66%, respectively. By catching and releasing the microwave photons from resonators64, our processor maybe play an important role in quantum communication.
Results
Quantum processor composed of resonators and a quantum bus
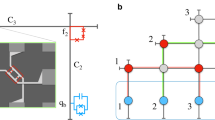
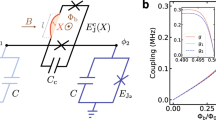
Our quantum processor is composed of some distant high-quality 1D superconducting resonators rj and a high-quality 1D superconducting resonator R, shown in Fig. 1. The common resonator R acts as a quantum bus for quantum information processing and it is capacitively coupled to a Ξ type three-energy-level superconducting transmon qutrit q whose frequency can be tuned by an external magnetic field. The qutrit is placed at the maximum of the voltage standing wave of R (not be drawn here). The simple superconducting quantum interferometer device (SQUID) with two Josephson junctions inserted between rj and R serves as the tunable-coupling function between them. The SQUID variables are not independent and introduce no new modes63. Here, the SQUIDs are not sensitive to the charge noise and can achieve a full tunability. Besides, the plasma frequencies of SQUIDs should be larger than the frequencies of the resonators. rj are laid far enough to each other to avoid their direct interaction generated by mutual capacitances and mutual inductive coupling. In the interaction picture, the Hamiltonian of the processor is (ħ = 1, under the rotating-wave approximation)

Here,  and Δj = ωj − ωR. ωR and ωj are the the first mode frequencies of R and rj, respectively. ωg,e(e,f) is the frequency of the transmon qutrit q with the transition
and Δj = ωj − ωR. ωR and ωj are the the first mode frequencies of R and rj, respectively. ωg,e(e,f) is the frequency of the transmon qutrit q with the transition 
 in which
in which  ,
,  and
and  are the ground, the first excited and the second excited states of the qutrit, respectively.
are the ground, the first excited and the second excited states of the qutrit, respectively.  and
and  are the creation operators of R and rj, respectively.
are the creation operators of R and rj, respectively.  and
and  are the creation operators of the two transitions of q, respectively. gg,e and ge,f
are the creation operators of the two transitions of q, respectively. gg,e and ge,f  are the coupling strengths between R and the two transitions of q, respectively. gj is the coupling strength between rj and R, which is contributed by their capacitive and inductive and can be tuned by the external flux through the SQUID63. By controlling the time dependence of the coupling, the cross-talk between resonators can be switched on and off.
are the coupling strengths between R and the two transitions of q, respectively. gj is the coupling strength between rj and R, which is contributed by their capacitive and inductive and can be tuned by the external flux through the SQUID63. By controlling the time dependence of the coupling, the cross-talk between resonators can be switched on and off.
The evolution of our processor can be described by the master equation65

Here, the operator D[L]ρ = (2LρL+ − L+Lρ − ρL+L)/2 (L = a, b,  ,
,  ).
).  and
and  . κ1, κ2 and κR are the decay rates of the resonators r1, r2 and R, respectively. γg,e (γe,f) is the energy relaxation rate of the qutrit with the transition
. κ1, κ2 and κR are the decay rates of the resonators r1, r2 and R, respectively. γg,e (γe,f) is the energy relaxation rate of the qutrit with the transition 
 . γϕ,e (γϕ,f) is the dephasing rate of the level
. γϕ,e (γϕ,f) is the dephasing rate of the level 
 of the qutrit. To achieve the resonance operations between R and rj, the transition frequencies of all the resonators are taken equal to each other.
of the qutrit. To achieve the resonance operations between R and rj, the transition frequencies of all the resonators are taken equal to each other.
Quantum state transfer between r1 and r2
Our quantum-state-transfer protocol between r1 and r2 can be completed with two resonance operations between the quantum bus R and the resonator rj. The interaction between R and rj can be described as

In our scheme, the states  ,
,  and
and  are required only. Here, the state
are required only. Here, the state  keeps unchanged with the evolution
keeps unchanged with the evolution  .
.  and
and  are the Fock states of R and rj, respectively.
are the Fock states of R and rj, respectively.  and
and  . For the resonance condition between R and rj (Δj = 0) and if we take the initial state of the subsystem composed of R and rj to be
. For the resonance condition between R and rj (Δj = 0) and if we take the initial state of the subsystem composed of R and rj to be  , the state of the system composed of R and rj can be expressed as (further details can be found in the method)
, the state of the system composed of R and rj can be expressed as (further details can be found in the method)

Our scheme for the quantum state transfer between the two resonators r1 and r2 can be accomplished with two-step resonance operations described in detail as follows.
Initially, we assume the initial state of the processor is

which means r1 is in the state  , R and r2 are all in the vacuum state and q is in the ground state. First, tuning the transition frequency of q to detune with R largely and turning off (on) the coupling strength between R and r2 (r1) by using the external flux through their SQUIDs, the state of the processor can evolve into
, R and r2 are all in the vacuum state and q is in the ground state. First, tuning the transition frequency of q to detune with R largely and turning off (on) the coupling strength between R and r2 (r1) by using the external flux through their SQUIDs, the state of the processor can evolve into

after a time of g1t = π/2.
Second, keeping the frequency of q detune with R largely, turning off g1 and turning on g2, the state of the processor can evolve from Eq. (6) to

within a time of g2t = π/2. Here, we complete the quantum state transfer as

If the operation time of the second step is taken as g2t = 3π/2, the final state after the information transfer is

This is just the result of the quantum state transfer between the two resonators r1 and r2 from the initial state  .
.
Controlled-phase gate on r1 and r2
C-phase gate is an important universal two-qubit gate. In the basis of two resonators  and
and 
 , a matrix of the gate can be expressed as
, a matrix of the gate can be expressed as

which means a minus phase should be generated if and only if the two qubits are in the state  . In our processor, the c-phase gate on the resonators r1 and r2 can be completed with five steps by combining the resonance operations between the quantum bus R and the resonator rj and those between R and q with the two transitions
. In our processor, the c-phase gate on the resonators r1 and r2 can be completed with five steps by combining the resonance operations between the quantum bus R and the resonator rj and those between R and q with the two transitions  and
and 
By taking the coupling strength between q and R much smaller than the anharmonicity of q (gg,e ≪ ωg,e − ωe,f), the interactions between R and q with the two transitions of  and
and  can be reduced into those of two individual two-energy-level qubits with R, whose Hamiltonians are
can be reduced into those of two individual two-energy-level qubits with R, whose Hamiltonians are

and

respectively. In the condition of resonance interactions between R and q with the transitions  (Δg,e = 0) and
(Δg,e = 0) and  (Δe,f = 0), the time-evolution operation of the system undergoing the Hamiltonians
(Δe,f = 0), the time-evolution operation of the system undergoing the Hamiltonians  and
and  are66
are66

and

respectively.
Supposing the initial state of the processor is

Here, the amplitudes α1 = cosθ1 cosθ2, α2 = cosθ1 sinθ2, α3 = sinθ1 cosθ2 and α4 = sinθ1 sinθ2. The five steps for the construction of our c-phase gate on r1 and r2 can be described in detail as follows.
First, turning on the coupling strength between R and r1 with g1 = gg,e and turning off the interaction between R and r2, the state of the processor can evolve from  to
to

with an operation time of  67.
67.
Second, tuning the frequency of q to detune with R largely and turning off the coupling between R and r1, one can get the state of the processor as

after the time of g2t = π/2 when the coupling between R and r2 is turned on.
Third, resonating R and q with the transition of  with a time of ge,ft = π and keeping R uncoupled to r1 and r2, the state of the the processor becomes
with a time of ge,ft = π and keeping R uncoupled to r1 and r2, the state of the the processor becomes

Fourth, repeating the second step, one can get the state of the processor as

Fifth, repeating the first step, we can get the state

This is just the result of our c-phase gate on r1 and r2 with the initial state  .
.
Possible experimental implementation
Resonance operation between a superconducting qubit and a 1D superconducting resonator has been used to achieve some basic tasks in quantum information processing, such as generating Fock states in a superconducting quantum circuit54, realizing the NOON state entanglement on two superconducting microwave resonators56, constructing the resonant quantum gates on charge qubits in circuit QED68 or on resonators59 and completing a fast scheme to generate NOON state entanglement on two resonators69. To get a high-fidelity resonant operation between the qubit and the resonator, the magnetic flux with fast tunability is required.
To show the performance of our schemes for quantum state transfer and the c-phase gate, we simulate their fidelities by using the whole Hamiltonian in each step. In our simulations, the parameters are chosen as: g1/(2π) and g2/(2π) can be tuned from 0 MHz to 50 MHz, ωR/(2π) = 6.65 GHz63, δ = ωg,e/(2π) − ωe,f/(2π) = 0.72 GHz70, gg,e/(2π) =  MHz,
MHz,  μs and
μs and  μs. The transition frequency of a transmon qutrit can be tune with a range of about 2.5 GHz71, which is enough for us to make it detune with R largely. The maximal values of g1/(2π) and g2/(2π) taken by us are 50 MHz as the rotation-wave approximation can work well when the coupling strength is much smaller than the frequency of R and a theoretic predict of the coupling strength between two superconducting resonators can reach 1.2 GHz63.
μs. The transition frequency of a transmon qutrit can be tune with a range of about 2.5 GHz71, which is enough for us to make it detune with R largely. The maximal values of g1/(2π) and g2/(2π) taken by us are 50 MHz as the rotation-wave approximation can work well when the coupling strength is much smaller than the frequency of R and a theoretic predict of the coupling strength between two superconducting resonators can reach 1.2 GHz63.
The process for the generation of the initial states of  and
and  are not included in our simulations. To prepare the initial states, one should perform a proper single-qubit operation on q and send the information from q to rj by using the resonance operation, the same as the one in the first step for the construction of our c-phase gate. Here, the interactions which do not attend the resonance operation should be turned off. The single-qubit operation on a superconducting qubit has been realized in experiment with a quantum error smaller than 0.000638, which has little influence on our schemes. By taking the energy relaxation rate of the qutrit, the decay rates of resonators and gg,e and gj into account, the generation of the initial states just increases a little error value of the fidelities of the quantum state transfer and the c-phase gate.
are not included in our simulations. To prepare the initial states, one should perform a proper single-qubit operation on q and send the information from q to rj by using the resonance operation, the same as the one in the first step for the construction of our c-phase gate. Here, the interactions which do not attend the resonance operation should be turned off. The single-qubit operation on a superconducting qubit has been realized in experiment with a quantum error smaller than 0.000638, which has little influence on our schemes. By taking the energy relaxation rate of the qutrit, the decay rates of resonators and gg,e and gj into account, the generation of the initial states just increases a little error value of the fidelities of the quantum state transfer and the c-phase gate.
Fidelity for our quantum state transfer
We numerically simulate the populations (vary with the operation time) of a microwave photon in r1, R and r2, shown in Fig. 2. The definition of the population is
The populations of a microwave photon in r1, R and r2. P1, P2 and P3 with the red, green and blue solid lines represent the populations of the microwave photon in r1, R and r2, respectively.
The inset shows the populations varying with the decay rates of the resonators, in which the solid, the dot dash and the dotted lines represent those with the decay rates of the resonators κ−1 = ∞ μs, κ−1 = 50 μs and κ−1 = 10 μs, respectively.

Here m = 1, 2, 3.  ,
,  and
and  . ρ(t) is the realistic density operator of the processor for the quantum state transfer from the initial state
. ρ(t) is the realistic density operator of the processor for the quantum state transfer from the initial state  . The parameters taken in the first step in our scheme are: ωg,e/(2π) = 5 GHz, g1/(2π) = 50 MHz, g2/(2π) = 0 MHz. In the second step, the parameters are: g1/(2π) = 0 MHz, g2/(2π) = 50 MHz and the other parameters are the same as the ones in the first step.
. The parameters taken in the first step in our scheme are: ωg,e/(2π) = 5 GHz, g1/(2π) = 50 MHz, g2/(2π) = 0 MHz. In the second step, the parameters are: g1/(2π) = 0 MHz, g2/(2π) = 50 MHz and the other parameters are the same as the ones in the first step.
From the numerical simulation, the quantum state transfer between r1 and r2 with θ = π/4 can reach a fidelity of 99.97% within 10 ns by using the definition of the fidelity as 
 with the initial state
with the initial state  . In the inset in Fig. 2, we give the three conditions of the populations with different decay rates of r1, r2 and R.
. In the inset in Fig. 2, we give the three conditions of the populations with different decay rates of r1, r2 and R.
Fidelity for our c-phase gate
We calculate the fidelity of our c-phase gate by using the average-gate-fidelity definition72,73

Here,  is the final state
is the final state  of the processor by using the ideal c-phase gate operation on the initial state
of the processor by using the ideal c-phase gate operation on the initial state  . ρ(t) is the realistic density operator after our c-phase gate operation on the initial state with the Hamiltonian H. The fidelity of our c-phase gate reaches 99.66% within 91.5 ns by using the parameters taken in each step as shown in Table 1. Here, if we take θ1 = θ2 = π/4 in Eq. (15) as an example, the density operators of
. ρ(t) is the realistic density operator after our c-phase gate operation on the initial state with the Hamiltonian H. The fidelity of our c-phase gate reaches 99.66% within 91.5 ns by using the parameters taken in each step as shown in Table 1. Here, if we take θ1 = θ2 = π/4 in Eq. (15) as an example, the density operators of  and the real final state are shown in Fig. 3(a,b), respectively.
and the real final state are shown in Fig. 3(a,b), respectively.
Actually, the fidelity of our c-phase gate is influenced by the decay rates κ of the resonators, the energy relaxation rate Γ of q and the anharmonicity δ of q, shown in Fig. 4. In Fig. 4(a), we show the fidelity of the gate varying with the decay rates and the energy relaxation rate of the resonators and q (κ = Γ). The fidelity of the gate is numerically simulated by using different optimal parameters corresponding to different Γ (keeping δ = 0.72 GHz unchanged) as the competition between the operation time (leads to the error from the coherence time of the qutrit) and the coupling strength between the qutrit and the bus R (leads to the error from the anharmonicity of the qutrit). Here, in order to choose Γ−1 = 10, 20, 30, 40 and 50 μs, we take  , 19, 13, 13 and 13 MHz, respectively. The corresponding operation times are t = 58.1, 65.8, 91.5, 91.5 and 91.5 ns, respectively. By using κ = ωr/Q (ωr is the frequency of the resonator)16, κ−1 = 50 μs corresponds to a quality factor Q ~ 2.08 × 106 of the resonators. In Fig. 4(b), the anharmonicity of the qutrit influences the fidelity with a small value as the coupling strength gg,e is much smaller than δ, which means that the transmon qutrit in our processor does not require a large anharmonicity.
, 19, 13, 13 and 13 MHz, respectively. The corresponding operation times are t = 58.1, 65.8, 91.5, 91.5 and 91.5 ns, respectively. By using κ = ωr/Q (ωr is the frequency of the resonator)16, κ−1 = 50 μs corresponds to a quality factor Q ~ 2.08 × 106 of the resonators. In Fig. 4(b), the anharmonicity of the qutrit influences the fidelity with a small value as the coupling strength gg,e is much smaller than δ, which means that the transmon qutrit in our processor does not require a large anharmonicity.
Conclusion
To show our processor can be used for an effective quantum computation based on resonators, we have given the scheme to achieve the quantum state transfer between two resonators and the one for the c-phase gate on them. These two schemes are just based on the Fock states  and
and  of the resonators rj. The fidelities of our quantum state transfer and c-phase gate reach 99.97% and 99.66% within 10 ns and 91.5 ns, respectively. In our processor, a single-qubit operation on the resonator rj can be achieved with the following steps: 1), one should transfer the information from rj to the qutrit with the resonance operation between them. 2), one can take the single-qubit gate on the qutrit. 3), one should transfer the information from the qutrit to rj. It is worth noticing that there are two steps with resonance operations in our scheme for the single-qubit operation on a microwave-photon resonator. Each resonance operation can generate a −phase for the state
of the resonators rj. The fidelities of our quantum state transfer and c-phase gate reach 99.97% and 99.66% within 10 ns and 91.5 ns, respectively. In our processor, a single-qubit operation on the resonator rj can be achieved with the following steps: 1), one should transfer the information from rj to the qutrit with the resonance operation between them. 2), one can take the single-qubit gate on the qutrit. 3), one should transfer the information from the qutrit to rj. It is worth noticing that there are two steps with resonance operations in our scheme for the single-qubit operation on a microwave-photon resonator. Each resonance operation can generate a −phase for the state  of the resonator rj or the state
of the resonator rj or the state  of the qutrit. The two steps with resonance operations can just eliminate this unwanted phase generated by each resonance operation as (−1)2 = 1. So, the single-qubit operation on the qutrit is convenient without considering the additional phase generated by the resonance operations. To readout the information of the photon states in rj, one can also transfer the information of the photon from rj (based on the Fock states
of the qutrit. The two steps with resonance operations can just eliminate this unwanted phase generated by each resonance operation as (−1)2 = 1. So, the single-qubit operation on the qutrit is convenient without considering the additional phase generated by the resonance operations. To readout the information of the photon states in rj, one can also transfer the information of the photon from rj (based on the Fock states  and
and  ) to the qutrit (based on the states
) to the qutrit (based on the states  and
and  and then readout the state of the qutrit. To achieve the quantum non-demolition detection on the resonator rj, one can use a low-quality resonator coupled to the qutrit q to detect the information in the quantum bus R55 which comes from rj. By using the resonators which can catch and release the microwave photons64, our processor maybe play an important role in quantum communication.
and then readout the state of the qutrit. To achieve the quantum non-demolition detection on the resonator rj, one can use a low-quality resonator coupled to the qutrit q to detect the information in the quantum bus R55 which comes from rj. By using the resonators which can catch and release the microwave photons64, our processor maybe play an important role in quantum communication.
In summary, we have proposed a quantum processor composed of some 1D superconducting resonators rj (quantum information carriers) which are coupled to a common 1D superconducting resonator R (the quantum bus), not the superconducting transmon qutrit, which makes it have the capability of integrating some distant resonators for quantum information processing on microwave photons assisted by circuit QED. With this processor, we have presented a scheme for the high-fidelity state transfer between two resonators. Also, we have given a scheme for the c-phase gate on two resonators with the resonance operations. With feasible parameters in experiment, the fidelities of our two schemes are 99.97% and 99.66%, respectively. Maybe this processor can play an important role in quantum communication in future.
Methods
Interaction between a resonator and a qubit
In the interaction picture, the Hamiltonian of a system composed of a two-energy-level qubit coupled to a resonator (Q-R system) can be written as (under the rotating-wave approximation):

Here, g is the coupling strength between the qubit and the resonator.  and a+ are the create operators of the qubit and the resonator, respectively. Δ = ωq − ωr. ωq (ωr) is the transition frequency of the qubit (resonator).
and a+ are the create operators of the qubit and the resonator, respectively. Δ = ωq − ωr. ωq (ωr) is the transition frequency of the qubit (resonator).
The state  of the Q-R system can be solved with the equation of motion
of the Q-R system can be solved with the equation of motion

in which  is a linear combination of the states
is a linear combination of the states  and
and  , that is,
, that is,

Here, ce,n(t) and cg,n(t) are the slowly varying probability amplitudes.  is the Fock state of the resonator. Because the only transitions between
is the Fock state of the resonator. Because the only transitions between  and
and  can be caused by the Hamiltonian HI, we just need to consider the evolutions of ce,n(t) and cg,n+1(t).
can be caused by the Hamiltonian HI, we just need to consider the evolutions of ce,n(t) and cg,n+1(t).
By combining Eqs. (24) and (25), one can get

A general solution for these amplitudes is

Here Ω2 = 4g2(n + 1) + Δ2.
Additional Information
How to cite this article: Hua, M. et al. Quantum state transfer and controlled-phase gate on one-dimensional superconducting resonators assisted by a quantum bus. Sci. Rep. 6, 22037; doi: 10.1038/srep22037 (2016).
References
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge University, Cambridge, 2000).
Shor, P. W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Sci. Statist. Comput. 26, 1484 (1997).
Grover, L. K. Quantum mechanics helps in searching for a needle in a haystack. Phys. Rev. Lett. 79, 325 (1997).
Long, G. L. Grover algorithm with zero theoretical failure rate. Phys. Rev. A 64, 022307 (2001).
Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46 (2001).
Ren, B. C. & Deng, F. G. Hyper-parallel photonic quantum computation with coupled quantum dots. Sci. Rep. 4, 4623 (2014).
Hu, C. Y. et al. Giant optical Faraday rotation induced by a single-electron spin in a quantum dot: Applications to entangling remote spins via a single photon. Phys. Rev. B 78, 085307 (2008).
Wei, H. R. & Deng, F. G. Scalable quantum computing based on stationary spin qubits in coupled quantum dots inside double-sided optical microcavities. Sci. Rep. 4, 7551 (2014).
Jones, J. A., Mosca, M. & Hansen, R. H. Implementation of a quantum search algorithm on a quantum computer. Nature 393, 344 (1998).
Long, G. L. & Xiao, L. Experimental realization of a fetching algorithm in a 7-qubit NMR spin Liouville space computer. J. Chem. Phys. 119, 8473 (2003).
Feng, G. R., Xu, G. F. & Long, G. L. Experimental realization of nonadiabatic holonomic quantum computation. Phys. Rev. Lett. 110, 190501 (2013).
Togan, E. et al. Quantum entanglement between an optical photon and a solid-state spin qubit. Nature 466, 730 (2010).
Neumann, P. et al. Quantum register based on coupled electron spins in a room-temperature solid. Nat. Phys. 6, 249 (2010).
Sillanpää, M. A., Park, J. I. & Simmonds, R. W. Coherent quantum state storage and transfer between two phase qubits via a resonant cavity. Nature 449, 438 (2007).
Majer, J. et al. Coupling superconducting qubits via a cavity bus. Nature 449, 443 (2007).
Blais, A. et al. Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation. Phys. Rev. A 69, 062320 (2004).
Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162 (2004).
Hu, Y. & Tian, L. Deterministic generation of entangled photons in superconducting resonator arrays. Phys. Rev. Lett. 106, 257002 (2011).
Miranowicz, A. et al. Two-photon and three-photon blockades in driven nonlinear systems. Phys. Rev. A 87, 023809 (2013).
Leghtas, Z. et al. Stabilizing a Bell state of two superconducting qubits by dissipation engineering. Phys. Rev. A 88, 023849 (2013).
Xue, Z. Y., Zhou, J. & Wang, Z. D. Universal holonomic quantum gates in decoherence-free subspace on superconducting circuits. Phys. Rev. A 92, 022320 (2015).
Sun, L. et al. Tracking photon jumps with repeated quantum non-demolition parity measurements. Nature 511, 444 (2014).
Rebić, S., Twamley, J. & Milburn, G. J. Giant Kerr Nonlinearities in Circuit Quantum Electrodynamics. Phys. Rev. Lett. 103, 150503 (2009).
Hu, Y. et al. Cross-Kerr-effect induced by coupled Josephson qubits in circuit quantum electrodynamics. Phys. Rev. A 84, 012329 (2011).
Du, L. H. Integrated photonic qubit quantum computing on a superconducting chip. New J. Phys. 12, 063015 (2010).
Yang, C. P., Chu, S. I. & Han, S. Y. Possible realization of entanglement, logical gates and quantum-information transfer with superconducting-quantum-interference-device qubits in cavity QED. Phys. Rev. A 67, 042311 (2003).
Yang, C. P., Chu, S. I. & Han, S. Y. Quantum Information Transfer and Entanglement with SQUID Qubits in Cavity QED: A Dark-State Scheme with Tolerance for Nonuniform Device Parameter. Phys. Rev. Lett. 92, 117902 (2004).
Chow, J. M. et al. Detecting highly entangled states with a joint qubit readout. Phys. Rev. A 81, 062325 (2010).
Cao, Y., Huo, W. Y., Ai, Q. & Long, G. L. Theory of degenerate three-wave mixing using circuit QED in solid-state circuits. Phys. Rev. A 84, 053846 (2011).
You, J. Q. & Nori, F. Atomic physics and quantum optics using superconducting circuits. Nature 474, 589 (2011).
Galiautdinov, A., Korotkov, A. N. & Martinis, J. M. Resonator-zero-qubit architecture for superconducting qubits. Phys. Rev. A 85, 042321 (2012).
Kelly, J. et al. State preservation by repetitive error detection in a superconducting quantum circuit. Nature 519, 66 (2015).
Hua, M., Tao, M. J., Deng, F. G. & Long, G. L. One-step resonant controlled phase gate on distant transmon qutrits in different 1D superconducting resonators. Sci. Rep. 5, 14541 (2015).
DiCarlo, L. et al. Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 460, 240 (2009).
DiCarlo, L. et al. Preparation and measurement of three-qubit entanglement in a superconducting circuit. Nature 467, 574 (2010).
Lucero, E. et al. Computing prime factors with a Josephson phase qubit quantum processor. Nat. Phys. 8, 719 (2012).
Reed, M. D. et al. Realization of three-qubit quantum error correction with superconducting circuits. Nature 482, 382 (2012).
Barends, R. et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 508, 500 (2014).
Megrant, A. et al. Planar superconducting resonators with internal quality factors above one million. Appl. Phys. Lett. 100, 113510 (2012).
Sandberg, M. et al. Tuning the field in a microwave resonator faster than the photon lifetime. Appl. Phys. Lett. 92, 203501 (2008).
Merkel, S. T. & Wilhelm, F. K. Generation and detection of NOON states in superconducting circuits. New J. Phys. 12, 093036 (2010).
Liao, J. Q. et al. Controlling the transport of single photons by tuning the frequency of either one or two cavities in an array of coupled cavities. Phys. Rev. A 81, 042304 (2010).
Strauch, F. W. Quantum logic gates for superconducting resonator qudits. Phys. Rev. A 84, 052313 (2011).
Eichler, C. et al. Observation of two-mode squeezing in the microwave frequency domain. Phys. Rev. Lett. 107, 113601 (2011).
Strauch, F. W., Onyango, D., Jacobs, K. & Simmonds, R. W. Entangled-state synthesis for superconducting resonators. Phys. Rev. A 85, 022335 (2012).
Li, P. B., Gao, S. Y. & Li, F. L. Engineering two-mode entangled states between two superconducting resonators by dissipation. Phys. Rev. A 86, 012318 (2012).
Chen, G. Y., Liu, M. H. & Chen, Y. N. Scattering of microwave photons in superconducting transmission-line resonators coupled to charge qubits. Phys. Rev. A 89, 053802 (2014).
Liu, Y. X. et al. Controllable microwave three-wave mixing via a single three-level superconducting quantum circuit. Sci. Rep. 4, 7289 (2014).
Wang, Y. P. et al. Realizing and characterizing chiral photon flow in a circuit quantum electrodynamics necklace. Sci. Rep. 5, 8352 (2015).
Hua, M., Tao, M. J. & Deng, F. G. Efficient generation of NOON states on two microwave-photon resonators. Chin. Sci. Bull 59, 2829 (2014).
Hua, M., Tao, M. J. & Deng, F. G. Universal quantum gates on microwave photons assisted by circuit quantum electrodynamics. Phys. Rev. A 90, 012328 (2014).
Johansson, J. R., Johansson, G. & Nori, F. Optomechanical-like coupling between superconducting resonators. Phys. Rev. A 90, 053833 (2014).
Houck, A. A. et al. Generating single microwave photons in a circuit. Nature 449, 328 (2007).
Hofheinz, M. et al. Generation of Fock states in a superconducting quantum circuit. Nature 454, 310 (2008).
Johnson, B. R. et al. Quantum non-demolition detection of single microwave photons in a circuit. Nat. Phys. 6, 663 (2010).
Wang, H. et al. Deterministic entanglement of photons in two superconducting microwave resonators. Phys. Rev. Lett. 106, 060401 (2011).
Strauch, F. W., Jacobs, K. & Simmonds, R. W. Arbitrary control of entanglement between two superconducting resonators. Phys. Rev. Lett. 105, 050501 (2010).
Yang, C. P., Su, Q. P., Zheng, S. B. & Han, S. Y. Generating entanglement between microwave photons and qubits in multiple cavities coupled by a superconducting qutrit. Phys. Rev. A 87, 022320 (2013).
Hua, M., Tao, M. J. & Deng, F. G. Fast universal quantum gates on microwave photons with all-resonance operations in circuit QED. Sci. Rep. 5, 9274 (2015).
Strauch, F. W. All-resonant control of superconducting resonators. Phys. Rev. Lett. 109, 210501 (2012).
Wu, C. W. et al. Scalable one-way quantum computer using on-chip resonator qubits. Phys. Rev. A 85, 042301 (2012).
Tsomokos, D. I., Ashhab, S. & Nori, F. Using superconducting qubit circuits to engineer exotic lattice systems. Phys. Rev. A 82, 052311 (2010).
Peropadre, B. et al. Tunable coupling engineering between superconducting resonators: From sidebands to effective gauge fields. Phys. Rev. B 87, 134504 (2013).
Yin, Y. et al. Catch and release of microwave photon states. Phys. Rev. Lett. 110, 107001 (2013).
Blais, A. et al. Quantum-information processing with circuit quantum electrodynamics. Phys. Rev. A 75, 032329 (2007).
Scully, M. O. & Zubairy, M. S. Quantum Optics (Cambridge University, Cambridge, 1997).
Tao, M. J., Hua, M., Ai, Q. & Deng, F. G. Quantum-information processing on nitrogen-vacancy ensembles with the local resonance assisted by circuit QED. Phys. Rev. A 91, 062325 (2015).
Haack, G. et al. Resonant quantum gates in circuit quantum electrodynamics. Phys. Rev. B 82, 024514 (2010).
Su, Q. P., Yang, C. P. & Zheng, S. B. Fast and simple scheme for generating NOON states of photons in circuit QED. Sci. Rep. 4, 3898 (2014).
Hoi, I. C. et al. Demonstration of a single-photon router in the microwave regime. Phys. Rev. Lett. 107, 073601 (2011).
Schreier, J. A. et al. Suppressing charge noise decoherence in superconducting charge qubits. Phys. Rev. B 77, 180502(R) (2008).
Yin, Z. Q. & Li, F. L. Multiatom and resonant interaction scheme for quantum state transfer and logical gates between two remote cavities via an optical fiber. Phys. Rev. A 75, 012324 (2007).
Johansson, J., Nation, P. & Nori, F. QuTiP: An open-source Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 183, 1760 (2012).
Acknowledgements
The simulations were coded in PYTHON using the QUTIP library. This work is supported by the China Postdoctoral Science Foundation under Grant No. 2015M581061, the National Natural Science Foundation of China under Grants No. 11474026 and the Fundamental Research Funds for the Central Universities under Grant No. 2015KJJCA01.
Author information
Authors and Affiliations
Contributions
M.H. and M.J. completed the calculation and prepared the figures. M.H. and F.G. wrote the main manuscript text. F.G. supervised the whole project. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Hua, M., Tao, MJ. & Deng, FG. Quantum state transfer and controlled-phase gate on one-dimensional superconducting resonators assisted by a quantum bus. Sci Rep 6, 22037 (2016). https://doi.org/10.1038/srep22037
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep22037
This article is cited by
-
Experimental realisation of tunable ferroelectric/superconductor \(({\text {B}} {\text {T}} {\text {O}}/{\text {Y}} {\text {B}}{\text {C}} {\text {O}})_{{\text {N}}}/{\text {S}}{\text {T}}{\text {O}}\) 1D photonic crystals in the whole visible spectrum
Scientific Reports (2020)
-
One-step transfer of quantum information for a photonic cat-state qubit
Quantum Information Processing (2020)
-
Perfect Quantum State Transfer in Glauber-Fock Cavity Array
International Journal of Theoretical Physics (2020)
-
Bell-state generation on remote superconducting qubits with dark photons
Quantum Information Processing (2018)
-
Multiple multicontrol unitary operations: Implementation and applications
Science China Physics, Mechanics & Astronomy (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.




 of our processor. (b) The realistic density operator
of our processor. (b) The realistic density operator  of the final state
of the final state  after our c-phase gate operation is performed on the two microwave-photon resonators. The color bar indicates the phase information of the density matrix elements.
after our c-phase gate operation is performed on the two microwave-photon resonators. The color bar indicates the phase information of the density matrix elements.