Abstract
We employ a positron annihilation technique, the spin-polarized two-dimensional angular correlation of annihilation radiation (2D-ACAR), to measure the spin-difference spectra of ferromagnetic nickel. The experimental data are compared with the theoretical results obtained within a combination of the local spin density approximation (LSDA) and the many-body dynamical mean-field theory (DMFT). We find that the self-energy defining the electronic correlations in Ni leads to anisotropic contributions to the momentum distribution. By direct comparison of the theoretical and experimental results we determine the strength of the local electronic interaction U in ferromagnetic Ni as 2.0 ± 0.1 eV.
Similar content being viewed by others
Introduction
The physical properties of ferromagnetic Ni are strongly influenced by correlation effects originating from the Coulomb interaction between electrons in the partially filled, relatively narrow 3d band1. Due to these correlations density functional theory (DFT)2,3,4 alone cannot explain various experimentally observed features of the electronic structure of Ni. To obtain a realistic description of the electronically correlated materials, parameters such as the local Coulomb repulsion U need to be employed. The “Hubbard” parameter U was originally introduced for single-band models5,6 and is defined as the Coulomb energy required to place two electrons on the same site:  . Here
. Here  represents the total energy of a system for which n electrons fill a given d-shell on a given atom. In multi-band systems U takes the form of an interaction matrix.
represents the total energy of a system for which n electrons fill a given d-shell on a given atom. In multi-band systems U takes the form of an interaction matrix.
The Hubbard model and related lattice models are able to explain important general features of correlated electrons, but they cannot describe the physics of real materials in detail. Namely, for an approach to be realistic it has to take into account the lattice and the explicit electronic structure of the systems. Here significant progress was made through the combination of DFT in the local density approximation (LDA) with dynamical mean field theory (DMFT)7,8,9,10 which is generally referred to as the LDA + DMFT method10,11. In the case of magnetic states the local spin density approximation (LSDA) rather than the LDA needs to be employed. In the L(S)DA + DMFT scheme the L(S)DA provides the ab initio material dependent input (orbitals and hoping parameters), while the DMFT solves the many-body problem for the local interactions. Therefore the LSDA + DMFT approach is able to compute, and even predict, properties of correlated materials. Considerable effort has been undertaken to construct systematic extensions beyond LSDA + DMFT in which ab-initio and interaction parameters are computed on the same footing in a self-consistent way. However, there remain many open questions due to the considerable algorithmical and numerical difficulties of the probelm (see ref. 10. and references therein).
Theoretical results obtained with LSDA + DMFT can be compared with experimental data obtained, for example, by photoemission spectroscopy (PES). In particular, this technique measures spectral functions, i.e., the imaginary part of the one-particle Green function, and thus determines correlation induced shifts of the spectral weight. This allows one to estimate the local Hubbard interaction U of a material, say, Ni. Indeed, most experimental investigations on the electronic structure of Ni rely on PES12,13. Braun et al.14 demonstrated the importance of local correlations in Ni by exploiting the magnetic circular dichroism in bulk sensitive soft X-ray PES measurements. One of the dominant correlation effects observed in the PES data for Ni is the satellite peak situated at 6 eV below the Fermi level15,16. This feature is not captured by LSDA, but is well explained by LSDA + DMFT17. LSDA + DMFT also reproduces the correct width of the occupied 3d bands and the exchange splitting17.
In this paper we discuss an alternative experimental technique to determine the local Coulomb parameter U, involving positrons. In contrast to photoelectron spectroscopy the theoretical analysis of positron spectroscopy does not suffer from complications due to external effects such as surfaces. We show that by combining experimental results of the spin-polarized two-dimensional angular correlation of annihilation radiation (2D-ACAR) with LSDA + DMFT computations including a careful and realistic treatment of the positron probe effects, it is possible to determine the strength of the electronic interactions in Ni quite unambiguously.
Results
In angular correlation measurements the quantity of interest is the probability per unit time and per unit volume in momentum space for the annihilating positron to produce two gamma quanta with a total momentum p, the so-called 2D-ACAR. If we assume for simplicity that the thermalized positron (with zero momentum at zero temeprature) has no correlations with the electrons then the 2D-ACAR gives directly the electron momentum probabilities. It is well known that both the shape and the structure of the 2D-ACAR probability distribution,  , are determined by the nature of wave functions of the electron and positron as well as by the topology of the Fermi surface. To obtain the latter we applied the Lock-Crisp-West (LCW) back-folding procedure both on the measured and the computed data. Since Ni is a ferromagnetic metal, spin-polarized 2D-ACAR measurements have been carried out. The spin-polarized 2D-ACAR measures the difference of the two spectra
, are determined by the nature of wave functions of the electron and positron as well as by the topology of the Fermi surface. To obtain the latter we applied the Lock-Crisp-West (LCW) back-folding procedure both on the measured and the computed data. Since Ni is a ferromagnetic metal, spin-polarized 2D-ACAR measurements have been carried out. The spin-polarized 2D-ACAR measures the difference of the two spectra  and is related to the spin-dependent momentum density of the material18.
and is related to the spin-dependent momentum density of the material18.  represents the experimental 2D-ACAR spectrum for the magnetization aligned parallel
represents the experimental 2D-ACAR spectrum for the magnetization aligned parallel  or anti-parallel
or anti-parallel  to the positron polarisation. The results are seen in Fig. 1. In each spectrum
to the positron polarisation. The results are seen in Fig. 1. In each spectrum  and
and  more than
more than  counts were collected, and the data were corrected for the momentum sampling function. Before subtraction, the spectra
counts were collected, and the data were corrected for the momentum sampling function. Before subtraction, the spectra  and
and  were normalized to an equal amount of counts. A renormalization due to 3γ decay was omitted since the corresponding correction in the case of Ni is negligible compared to the statistical noise18. The expected 4-fold symmetry is clearly observed and the anisotropy is found to be in good agreement with the study of Genould et al.19. The inset in Fig. 1 shows that the anisotropy of the magnetic signal,
were normalized to an equal amount of counts. A renormalization due to 3γ decay was omitted since the corresponding correction in the case of Ni is negligible compared to the statistical noise18. The expected 4-fold symmetry is clearly observed and the anisotropy is found to be in good agreement with the study of Genould et al.19. The inset in Fig. 1 shows that the anisotropy of the magnetic signal,  , is more pronounced along the Γ – X – Γ direction than along the Γ – L – Γ direction. This is also in accordance with the calculations of Nagoa et al.20. The comparison between the experimental and theoretical spin-polarized 2D-ACAR data is presented in Fig. 2. Both spectra have been back-folded using the LCW-procedure. The central plot represents the measured spectra, and is surrounded by theoretical results obtained from LSDA + DMFT performed for several values of U. Our results show significant electronic correlations effects. It is clearly seen that with increasing U a gap opens at the L-points of the Brillouin zone. This gap is associated with the necks in the Fermi surface of Ni. This implies that LSDA underestimates the density at the X-point, while the density near the L-point is overestimated. In the LSDA + DMFT calculation the highest density is found at the X-point, similar to the experiment. However, the structure connecting the X and L-points is less pronounced in the experimental data than in the LSDA + DMFT results. Apparently the local interaction (see e.g.14) pushes the d-bands below the Fermi energy, whereby the X2 hole pocket obtained in LSDA disappears. This is a general feature of electronic correlations in Ni21 and also greatly changes the calculated anomalous Hall effect of Ni22,23. Therefore, our experiment is able to identify the electronic correlations as the origin of anomalous Hall resistivity in bulk Ni.
, is more pronounced along the Γ – X – Γ direction than along the Γ – L – Γ direction. This is also in accordance with the calculations of Nagoa et al.20. The comparison between the experimental and theoretical spin-polarized 2D-ACAR data is presented in Fig. 2. Both spectra have been back-folded using the LCW-procedure. The central plot represents the measured spectra, and is surrounded by theoretical results obtained from LSDA + DMFT performed for several values of U. Our results show significant electronic correlations effects. It is clearly seen that with increasing U a gap opens at the L-points of the Brillouin zone. This gap is associated with the necks in the Fermi surface of Ni. This implies that LSDA underestimates the density at the X-point, while the density near the L-point is overestimated. In the LSDA + DMFT calculation the highest density is found at the X-point, similar to the experiment. However, the structure connecting the X and L-points is less pronounced in the experimental data than in the LSDA + DMFT results. Apparently the local interaction (see e.g.14) pushes the d-bands below the Fermi energy, whereby the X2 hole pocket obtained in LSDA disappears. This is a general feature of electronic correlations in Ni21 and also greatly changes the calculated anomalous Hall effect of Ni22,23. Therefore, our experiment is able to identify the electronic correlations as the origin of anomalous Hall resistivity in bulk Ni.
In order to derive the value of the local Coulomb interaction parameter U from our experiment we performed a least square fit  analysis of the measured data with the LSDA + DMFT calculations (Fig. 2). To assess the importance of the electron-positron correlation, two sets of LSDA + DMFT computations have been performed, one without and one with the electron-positron interaction. The results for
analysis of the measured data with the LSDA + DMFT calculations (Fig. 2). To assess the importance of the electron-positron correlation, two sets of LSDA + DMFT computations have been performed, one without and one with the electron-positron interaction. The results for  without the electron-positron interaction (“independent particle model” (IPM)) are shown in Fig. 3 by a dashed yellow line. However, the electron-positron attraction should not be neglected since it leads to an increase of electron density at the positron, which is refered to as “enhancement” since the total annihilation rate strongly increases. Indeed, the inclusion of the electron-positron interaction by the so-called enhancement factor (a multiplicative factor in the product of the electron and positron wave functions) changes
without the electron-positron interaction (“independent particle model” (IPM)) are shown in Fig. 3 by a dashed yellow line. However, the electron-positron attraction should not be neglected since it leads to an increase of electron density at the positron, which is refered to as “enhancement” since the total annihilation rate strongly increases. Indeed, the inclusion of the electron-positron interaction by the so-called enhancement factor (a multiplicative factor in the product of the electron and positron wave functions) changes  substantially: now a clear minimum in
substantially: now a clear minimum in  is found (dashed blue line). A more detailed discussion of the enhancement factor is presented in the following section. The minimum in
is found (dashed blue line). A more detailed discussion of the enhancement factor is presented in the following section. The minimum in  is found at
is found at  eV. The 2D-ACAR spectra can be projected along different directions in mometum space as shown in the inset of Fig. 3. The
eV. The 2D-ACAR spectra can be projected along different directions in mometum space as shown in the inset of Fig. 3. The  curves of the 1D data exhibit minima for the value of
curves of the 1D data exhibit minima for the value of  eV for the Hubbard interaction similar to the 2D-ACAR spectra. The loss of information in the doubly integrated 1D data is indicated by a larger
eV for the Hubbard interaction similar to the 2D-ACAR spectra. The loss of information in the doubly integrated 1D data is indicated by a larger  value. We also note that the effects of electron-electron correlations within the LSDA + DMFT on the electron density are anisotropic and therefore go beyond an isotropic Lam-Platzman24 correction of the LSDA data. Interpolating the data in Fig. 3 with higher order polynomials allows us to estimate the systematic error in the position of the absolute minimum as ±0.1 eV.
value. We also note that the effects of electron-electron correlations within the LSDA + DMFT on the electron density are anisotropic and therefore go beyond an isotropic Lam-Platzman24 correction of the LSDA data. Interpolating the data in Fig. 3 with higher order polynomials allows us to estimate the systematic error in the position of the absolute minimum as ±0.1 eV.
Discussion
There exist a number of experimental studies on the numerical value of the local Hubbard interaction U in Ni. Specifically, J. Braun et al. (ref. 14) as well as J. Sánchez-Barriga et al. (ref. 15) present results on photoelectron emission studies. While ref. 14 reports on soft x-ray ARPES on bulk Ni, ref. 15 discusses spin resolved ultra-violet ARPES obtained on Ni films grown epitaxially on a tungsten substrate. In an approach that is conceptually similar to ours, they model the experimental energy distribution curves in a LSDA + DMFT framework using a one step model and conclude that U in the range of 2.5 to 2.8 eV gives an optimal fit. A somewhat smaller value for U is reported in the study of the anomalous Hall effect in Ni by Ködderitzsch et al., yielding a value for the Hubbard interaction parameter of  eV23. Modelling experimental Compton scattering profiles25 by LSDA + DMFT26,27 gives yet smaller values of
eV23. Modelling experimental Compton scattering profiles25 by LSDA + DMFT26,27 gives yet smaller values of  to 2.3 eV, similar to the value of
to 2.3 eV, similar to the value of  eV as reported here.
eV as reported here.
At first sight, the variation in the values of U determined by the various experimental methods seems displeasing. However, we want to point out the aspect of the electronic states sampled by the methods, specifically with respect to the electron binding energies: In spin-polarized 2D-ACAR electrons close to the Fermi energy contribute most to the measured two-photon-momentum-distributions due to the sampling by the positron (wave-function and correlation effects). In magnetic Compton scattering all electrons contribute equally to the measured Compton profiles as the scattering cross section is virtually independent of the binding energy. Furthermore, in the anomalous Hall effect the electrons in the region with a high density-of-states contribute the most, whereas in photoemission spectroscopy electrons with even higher binding energies (up to −10 eV) are considered.
Therefore, we conclude that while the theoretical modelling of the various methods assumes a single value of U, in reality different electronic states would correspond to different values, which are sampled by the diverse experimental methods. In addition, one has to bear in mind that while anomalous Hall effect measurements similarly to Compton or positron-annihilation experiments are bulk sensitive techniques, photo-electron spectroscopy is fairly surface sensitive. In a first approximation it is therefore expected to find a larger value of U due to a reduced number of nearest neighbours that screen the value of U at the surface.
Furthermore, we also take the opportunity to discuss the electron-positron correlation effects in Ni. A fundamental question in positron annihilation in solids is how the electron-positron interaction modifies the electronic structure of the medium which is being probed. The electron-positron attraction leads to an increase of electron density at the positron, which manifests itself in the annihilation characteristics. This effect is called “enhancement” and is qualitatively well understood: the total annihilation rate is strongly increased. However, apart from the short-range screening, the electronic states and the mean density remain almost unchanged. Therefore, the 2D-ACAR shows only relatively weak differences compared to the independent particle model (IPM). In the case of alkali metals the enhancement effect is included by multiplying the 2D-ACAR spectra computed in the independent particle model with an isotropic enhancement factor28,29, the so-called Kahana factor. This approach was generalized to an energy dependent form30, and was later extended to an orbital dependence31. It was formulated within DFT32,33,34,35,36,37,38,39,40,41,42 and therefore maintains its static mean-field character. Different parametrizations of the enhancement functional have been proposed in the literature32,39,40,43,44,45,46 and applied in the case of Ni31,47.
Biasini et al.48,49. proposed that probe effects associated with electron-positron interaction, such as positron wave function effects, can be partially avoided by applying magnetic 2D-ACAR. We have tested this conjecture, by computing the 2D-ACAR spectra in the presence and absence, respectively, of the positron, with and without electronic and electron-positron correlations. The electron-positron interaction was included in the form of an effective one-particle potential as formulated in DFT by Boronski and Nieminen32.
We analyzed our results by taking several cuts along the symmetry directions in the Brillouin zone. Since the positron affects the individual spin channels differently we plot in Fig. 4 the spin-contrast,  , which was computed within LSDA and LSDA + DMFT, respectively. Within LSDA the spin difference is found to be essentially independent of the presence of the positron. In particular, it remains essentially the same along the symmetry lines in the Brillouin zone. Once electronic correlations are included by DMFT a clear difference in the results for the spin-contrast in the presence and absence, respectively, of the positron is found. The results show that the conjecture of Biasini et al.48,49 regarding the cancelation of probe effects in spin-polarized 2D-ACAR is not valid beyond LSDA, i.e., when many-body effects are included. The cancelation appears to be a consequence of the form of the electron-electron and electron-positron correlation functionals in the LSDA, which have a very similar mean-field structure.
, which was computed within LSDA and LSDA + DMFT, respectively. Within LSDA the spin difference is found to be essentially independent of the presence of the positron. In particular, it remains essentially the same along the symmetry lines in the Brillouin zone. Once electronic correlations are included by DMFT a clear difference in the results for the spin-contrast in the presence and absence, respectively, of the positron is found. The results show that the conjecture of Biasini et al.48,49 regarding the cancelation of probe effects in spin-polarized 2D-ACAR is not valid beyond LSDA, i.e., when many-body effects are included. The cancelation appears to be a consequence of the form of the electron-electron and electron-positron correlation functionals in the LSDA, which have a very similar mean-field structure.
Methods
Spin-polarized 2D-ACAR.
For a detailed description of the basic 2D-ACAR technique we refer to refs 50, 51, 52.
The spin-polarized variant of 2D-ACAR relies on two aspects: the non-zero net polarisation of positrons from a radioactive source, which was determined as 31(4)% in a separate experiment, and the fact that positron annihilation occurs mainly when the spins of positron and electron are aligned anti-parallel. Spin-polarized 2D-ACAR is one of the few experimental methods that can probe the momentum distribution of the electrons in the bulk with respect to the spin direction and even at elevated temperatures. It was successfully applied to elemental Ni19,53,54 and other materials55,56,57,58.
We measured spin-resolved 2D-ACAR in magnetic fields up to 1.1 T at room temperature. The field was applied parallel and anti-parallel, respectively, relative to the crystallographic  orientation of the sample which coincides with the emission direction of the positrons (i.e. the polarisation direction of the positron beam) as well as the magnetic easy-axis of Ni. When an external magnetic field is applied parallel or anti-parallel to the emission direction the positrons will annihilate predominantly with electrons from the majority or the minority spin directions, respectively (see Fig. 5).
orientation of the sample which coincides with the emission direction of the positrons (i.e. the polarisation direction of the positron beam) as well as the magnetic easy-axis of Ni. When an external magnetic field is applied parallel or anti-parallel to the emission direction the positrons will annihilate predominantly with electrons from the majority or the minority spin directions, respectively (see Fig. 5).
LSDA+DMFT
The theoretical analysis of the 2D-ACAR spectra requires the knowledge of the two-particle electron-positron Green function, describing the probability amplitude for an electron and a positron propagating between two different space-time points. This two particle many-body problem is factorized into the many-body electronic and the one-body positronic part. The DFT can be generalized to electron-positron systems by including the positron density, in the form of the 2-component DFT32,59. The electron-positron correlations are taken into account by a multiplicative factor, the so-called enhancement factor, briefly discussed above. Within DFT the enhancement factor is treated as a functional of the electron density in the local density approximation59.
Electronic structure calculations were performed with the spin-polarized relativistic Korringa-Kohn-Rostoker (SPR-KKR) method60. For LSDA computations the exchange-correlation potentials parametrized by Vosko, Wilk and Nusair61 were used with a lattice parameter of 3.52 Å. To include the electronic correlations, a charge and self-energy self-consistent LSDA + DMFT scheme was employed, which is based on the KKR approach62 and where the impurity problem is solved with a spin-polarized T-matrix fluctuation exchange method63,64. This impurity solver is fully rotationally invariant even in the multi-orbital version and is reliable when the interaction U is smaller than the bandwidth, a condition which is fulfilled in the case of Ni. In this LSDA + DMFT framework the electron-positron momentum density  is computed directly from the two-particle Green function in the momentum representation. The neglect of electron-positron correlations corresponds to the factorization of the two-particle Green function in real space. In the numerical implementation the position-space integrals for the “auxiliary” Green function
is computed directly from the two-particle Green function in the momentum representation. The neglect of electron-positron correlations corresponds to the factorization of the two-particle Green function in real space. In the numerical implementation the position-space integrals for the “auxiliary” Green function  obtained within LSDA or LSDA + DMFT, respectively, are performed as integrals over unit cells:
obtained within LSDA or LSDA + DMFT, respectively, are performed as integrals over unit cells:

where X = LSDA or LSDA + DMFT, and  , and
, and  are the momenta and spin of electron and positron, respectively. Here
are the momenta and spin of electron and positron, respectively. Here  is computed for each energy point on the complex energy contour, providing the electron-positron momentum density:
is computed for each energy point on the complex energy contour, providing the electron-positron momentum density:

Integration over positron energies  is not required, since only the ground state is considered, and
is not required, since only the ground state is considered, and  at the annihilation. The momentum carried off by the photons is equal to that of the two particles up to a reciprocal lattice vector, reflecting the fact that the annihilation takes place in a crystal. Hence an electron with wave vector k contributes to
at the annihilation. The momentum carried off by the photons is equal to that of the two particles up to a reciprocal lattice vector, reflecting the fact that the annihilation takes place in a crystal. Hence an electron with wave vector k contributes to  not only at
not only at  (normal process) but also at
(normal process) but also at  , with K a vector of the reciprocal lattice (Umklapp process). The experimental spin-difference spectra
, with K a vector of the reciprocal lattice (Umklapp process). The experimental spin-difference spectra  can be compared with the computed difference in the integrated momentum densities of Eq. 2:
can be compared with the computed difference in the integrated momentum densities of Eq. 2:

In a perfect bulk material the 2D-ACAR distributions are rather anisotropic, reflecting the fact that certain valence bands in certain directions in the Brillouin zone do not contribute to the momentum density of annihilating electron-positron pairs. One can define the spin-difference spectra: 
 which was compared with the corresponding experimentally measured spectra
which was compared with the corresponding experimentally measured spectra  taken in the presence of the magnetic field. Here the annihilation probability for the triplet electron-positron pair is neglected since it is of order 10-3 smaller than that of the singlet annihilation.
taken in the presence of the magnetic field. Here the annihilation probability for the triplet electron-positron pair is neglected since it is of order 10-3 smaller than that of the singlet annihilation.
In order to assess the impact of the presence of the positron, the electronic momentum density was computed from the Green function in the momentum representation, as used in the calculations of the Compton profiles:

which formally corresponds to Eq. 1 if the positronic Green function is removed. The spin projected momentum density is obtained according to the formula:

LCW backfolding
Our analysis concerns the two-dimensional projections of the electronic momentum densities with the integration direction chosen along [100]. The LCW folding procedure65 is used for the momentum densities:

with K the reciprocal lattice vector. In the presence of the positron  is replaced by
is replaced by  (Eq. 2), while in the absence of the positron
(Eq. 2), while in the absence of the positron  (Eq. 5) takes the place of
(Eq. 5) takes the place of  in Eq. 6.
in Eq. 6.
The LCW procedure is exact when applied to the electronic momentum density. In the presence of the positron the back-folding procedure is only exact if the positron wave function is a plane wave. If the positron wave function varies in k, completely filled bands also give rise to variations in  . However, the amplitude of the positron wave function varies slowly within the Brillouin zone and therefore the variations in
. However, the amplitude of the positron wave function varies slowly within the Brillouin zone and therefore the variations in  are also expected to be smooth66,67.
are also expected to be smooth66,67.
Sample preparation and characterisation
The Ni crystal (purity 99.99%), with dimensions of  mm × 1 mm, was obtained from MaTecK GmbH. The top surface of the sample is orientated along [110] with an accuracy of ±0.1° and was polished to a surface roughness <50 nm. Positron lifetime measurements prior to the 2D-ACAR measurements revealed only a single lifetime of 113 ps in agreement with the bulk value of Nickel. Hence, it can be safely assumed that the sample is defect-free. Prior to mounting the sample in the spectrometer the orientation of the [100] integration direction was determined by Laue diffraction to ±1°.
mm × 1 mm, was obtained from MaTecK GmbH. The top surface of the sample is orientated along [110] with an accuracy of ±0.1° and was polished to a surface roughness <50 nm. Positron lifetime measurements prior to the 2D-ACAR measurements revealed only a single lifetime of 113 ps in agreement with the bulk value of Nickel. Hence, it can be safely assumed that the sample is defect-free. Prior to mounting the sample in the spectrometer the orientation of the [100] integration direction was determined by Laue diffraction to ±1°.
Additional Information
How to cite this article: Ceeh, H. et al. Local electron-electron interaction strength in ferromagnetic nickel determined by spin-polarized positron annihilation. Sci. Rep. 6, 20898; doi: 10.1038/srep20898 (2016).
Change history
13 April 2016
A correction has been published and is appended to both the HTML and PDF versions of this paper. The error has been fixed in the paper.
References
Lichtenstein, A. I., Katsnelson, M. I. & Kotliar, G. Spectral density functional approach to electronic correlations and magnetism in crystals . 75 (Kluwer Academic/Plenum, New York, 2002).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev . 136, B864–B871 (1964).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev . 140, A1133–A1138 (1965).
Kohn, W. Nobel lecture: Electronic structure of matter-wave functions and density functionals. Rev. Mod. Phys. 71, 1253–1266 (1999).
Hubbard, J. Electron correlations in narrow energy bands. Proc. R. Soc. London 276, 238–257 (1963).
Gutzwiller, M. C. Effect of correlation on the ferromagnetism of transition metals. Phys. Rev. Lett. 10, 159–163 (1963).
Metzner, W. & Vollhardt, D. Correlated lattice fermions in d = ∞ dimensions. Phys. Rev. Lett. 62, 324–327 (1989).
Georges, A., Kotliar, G., Krauth, W. & Rozenberg, M. J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 68, 13–125 (1996).
Kotliar, G. & Vollhardt, D. Strongly correlated materials: Insights from dynamical mean-field theory. Phys. Today 57, 53–59 (2004).
Kotliar, G. et al. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 78, 865–951 (2006).
Held, K. Electronic structure calculations using dynamical mean field theory. Adv. Phys . 56, 829–926 (2007).
Aebi, P. et al. k-space mapping of majority and minority bands on the Fermi surface of nickel below and above the Curie temperature. Phys. Rev. Lett. 76, 1150–1153 (1996).
Schneider, C. M., Pracht, U., Kuch, W., Chassé, A. & Kirschner, J. Magnetic dichroism in photoemission as a spin-resolving probe for electronic correlations. Phys. Rev. B 54, R15618–R15621 (1996).
Braun, J. et al. Correlation effects, circular dichroism, and Fermi surfaces of bulk nickel from soft x-ray angle-resolved photoemission. Phys. Rev. B 85, 165105 (2012).
Sánchez-Barriga, J. et al. Effects of spin-dependent quasiparticle renormalization in Fe, Co, and Ni photoemission spectra: an experimental and theoretical study. Phys. Rev. B 85, 205109 (2012).
Himpsel, F. J., Knapp, J. A. & Eastman, D. E. Experimental energy-band dispersions and exchange splitting for Ni. Phys. Rev. B 19, 2919–2927 (1979).
Lichtenstein, A. I., Katsnelson, M. I. & Kotliar, G. Finite-temperature magnetism of transition metals: An ab initio dynamical mean-field theory. Phys. Rev. Lett. 87, 067205 (2001).
Berko, S. & Mills, A. P. Spin distribution studies in ferromagnetic metals by polarized positron annihilation experiments. J. Phys. Coll. 32, C1-287–C1-289 (1971).
Genoud, P., Manuel, A. A., Walker, E. & Peter, M. Spin-polarized 2D ACAR in nickel across the Curie temperature. J. Phys. Condens. Mat . 3, 4201 (1991).
Nagao, T. et al. Momentum-density distribution of magnetic electrons in ferromagnetic nickel. J. Phys. Condens. Mat. 20, 055201 (2008).
Wang, C. S. & Callaway, J. Energy bands in ferromagnetic nickel. Phys. Rev. B 15, 298–306 (1977).
Fuh, H.-R. & Guo, G.-Y. Intrinsic anomalous hall effect in nickel: A GGA + U study. Phys. Rev. B 84, 144427 (2011).
Ködderitzsch, D., Chadova, K., Minár, J. & Ebert, H. Impact of finite temperatures and correlations on the anomalous hall conductivity from ab initio theory. New J. Phys. 15, 053009 (2013).
Lam, L. & Platzman, P. M. Momentum density and compton profile of the inhomogeneous interacting electronic system. I. Formalism. Phys. Rev. B 9, 5122–5127 (1974).
Dixon, M. A. G. et al. Spin density in ferromagnetic nickel: a magnetic compton scattering study. J. Phys. Condens. Mat. 10, 2759 (1998).
Chioncel, L., Benea, D., Ebert, H., Di Marco, I. & Minár, J. Momentum space anisotropy of electronic correlations in Fe and Ni: An analysis of magnetic compton profiles. Phys. Rev. B 89, 094425 (2014).
Chioncel, L., Benea, D., Mankovsky, S., Ebert, H. & Minár, J. Static corrections versus dynamic correlation effects in the valence band compton profile spectra of Ni. Phys. Rev. B 90, 184426 (2014).
Kahana, S. Positron annihilation in metals. Phys. Rev . 129, 1622–1628 (1963).
Carbotte, J. P. & Kahana, S. Positron annihilation in an interacting electron gas. Phys. Rev . 139, A213–A222 (1965).
Mijnarends, P. E. & Singru, R. M. Point-geometry angular correlation curves for Cu: A study of enhancement in positron annihilation. Phys. Rev. B 19, 6038–6048 (1979).
Singh, A. et al. Study of the many-body correlation effects in nickel by positron annihilation. Helv. Phys. Act . 59, 410–416 (1986).
Boroński, E. & Nieminen, R. M. Electron-positron density-functional theory. Phys. Rev. B 34, 3820–3831 (1986).
Rubaszek, A. & Stachowiak, H. Self-consistent solution of the Kahana equation for a positron in an electron gas. Phys. Rev. B 38, 3846–3855 (1988).
Barbiellini, B., Puska, M. J., Torsti, T. & Nieminen, R. M. Gradient correction for positron states in solids. Phys. Rev. B 51, 7341–7344 (1995).
Barbiellini, B. et al. Calculation of positron states and annihilation in solids: A density-gradient-correction scheme. Phys. Rev. B 53, 16201–16213 (1996).
Barbiellini, B., Hakala, M., Puska, M. J., Nieminen, R. M. & Manuel, A. A. Correlation effects for electron-positron momentum density in solids. Phys. Rev. B 56, 7136–7142 (1997).
Sormann, H. Influence of lattice effects on the electron-positron interaction in metals. Phys. Rev. B 54, 4558–4580 (1996).
Sormann, H. & Kontrym-Sznajd, G. Many-body effects on the electron-positron momentum density in simple and transition metals: Comparison with positron annihilation spectroscopy data. Phys. Rev. B 73, 075111 (2006).
Kontrym-Sznajd, G. & Sormann, H. & Boroński, E. General properties of electron-positron momentum densities. Phys. Rev. B 85, 245104 (2012).
Kontrym-Sznajd, G. & Sormann, H. The influence of a positron on electron-positron momentum densities in metallic materials. Phys. Scripta 89, 015808 (2014).
Kontrym-Sznajd, G. & Sormann, H. Electron-positron momentum densities in crystalline solids. Phys. Status Solidi (b) 251, 140–147 (2014).
Boroński, E. Influence of many-body effects in real metals on electron-positron momentum distributions. Acta Phys. Pol. A 125, 706–709 (2014).
Singh, A. K. & Jarlborg, T. Calculation of compton profiles and positron annihilation matrix elements using LMTO wavefunctions. J. Phys. F Met. Phys . 15, 727 (1985).
Jarlborg, T. & Singh, A. K. Local-density approach for calculation of electron-positron enhancement in transition metals. Phys. Rev. B 36, 4660–4663 (1987).
Laverock, J., Haynes, T. D., Alam, M. A. & Dugdale, S. B. Experimental determination of the state-dependent enhancement of the electron-positron momentum density in solids. Phys. Rev. B 82, 125127 (2010).
Makkonen, I., Ervasti, M. M., Siro, T. & Harju, A. Enhancement models of momentum densities of annihilating electron-positron pairs: The many-body picture of natural geminals. Phys. Rev. B 89, 041105 (2014).
Kontrym-Sznajd, G. et al. Investigation of the electronic structure of ferro- and paramagnetic nickel by positron annihilation. Appl. Phys . 8, 151–162 (1975).
Biasini, M. & Rusz, J. Cancellation of probe effects in measurements of spin-polarized momentum density by electron-positron annihilation. J. Phys. Condens. Mat . 18, L289 (2006).
Rusz, J. & Biasini, M. Positron wave-function effects in the measurement of the two-dimensional angular correlation of the annihilation radiation of a spin-polarized system. Phys. Rev. B 75, 235115 (2007).
West, R. N., Mayers, J. & Walters, P. A. A high-efficiency two-dimensional angular correlation spectrometer for positron studies. J. Phys. E Sci. Instrum . 14, 478 (1981).
Ceeh, H., Weber, J. A., Leitner, M., Böni, P. & Hugenschmidt, C. The source-sample stage of the new two-dimensional angular correlation of annihilation radiation spectrometer at Technische Universität München. Rev. Sci. Instr. 84, 043905 (2013).
Leitner, M., Ceeh, H. & Weber, J.-A. Eliminating spatial distortions in Anger-type gamma cameras. New J. Phys. 14, 123014 (2012).
Berko, S. & Zuckerman, J. Polarized positron annihilation in ferromagnets. Phys. Rev. Lett. 13, 339–341 (1964).
Mihalisin, T. W. & Parks, R. D. Anisotropic spin polarization in ferromagnetic nickel. Phys. Rev. Lett. 18, 210–211 (1967).
Hanssen, K. E. H. M. & Mijnarends, P. E. Positron-annihilation study of the half-metallic ferromagnet NiMnSb: Theory. Phys. Rev. B 34, 5009–5016 (1986).
Hanssen, K. E. H. M., Mijnarends, P. E., Rabou, L. P. L. M. & Buschow, K. H. J. Positron-annihilation study of the half-metallic ferromagnet NiMnSb: Experiment. Phys. Rev. B 42, 1533–1540 (1990).
Livesay, E. A., West, R., Dugdale, S. B., Santi, G. & Jarlborg, T. A spin-polarized 2D-ACAR study of the colossal magnetoresistive material La0.7Sr0.3MnO3 . Mater. Sci. Forum 363–365, 576 (2001).
Haynes, T. D. et al. Positron annihilation study of the Fermi surface of Ni2MnGa. New J. Phys. 14, 035020 (2012).
Puska, M. J. & Nieminen, R. M. Theory of positrons in solids and on solid surfaces. Rev. Mod. Phys. 66, 841–897 (1994).
Ebert, H., Ködderitzsch, D. & Minár, J. Calculating condensed matter properties using the KKR-Green's function method-recent developments and applications. Rep. Prog. Phys. 74, 096501 (2011).
Vosko, S. H., Wilk, L. & Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis. Can. J. Phys. 58, 1200 (1980).
Minár, J. et al. Multiple-scattering formalism for correlated systems: A KKR-DMFT approach. Phys. Rev. B 72, 045125 (2005).
Lichtenstein, A. I. & Katsnelson, M. I. Ab initio calculations of quasiparticle band structure in correlated systems: LDA++ approach. Phys. Rev. B 57, 6884–6895 (1998).
Pourovskii, L., Katsnelson, M. & Lichtenstein, A. Correlation effects in electronic structure of actinide monochalcogenides. Phys. Rev. B 72, 115106 (2005).
Lock, D. G., Crisp, V. H. C. & West, R. N. Positron annihilation and Fermi surface studies: a new approach. J. Phys. F Met. Phys . 3, 561 (1973).
West, R. Positron studies of the electronic structure of metals and alloys. In Positron studies of solids, surfaces, and atoms: a symposium to celebrate Stephan Berko's 60th birthday, Brandeis University, December 12, 1984, 48 (World Scientific Pub Co Inc, 1986).
Rabou, L. & Mijnarends, P. Approximate validity of the Lock-Crisp-West theorem in positron annihilation. Solid State Commun. 52, 933- 936 (1984).
Acknowledgements
This project was funded by the Deutsche Forschungsgesellschaft (DFG) through the Transregional Collaborative Research Center TRR 80 and Research Unit FOR1346. DB acknowledges the DAAD, the CNCS - UEFISCDI(PN-II-ID-PCE-2012-4-0470) and the COST Action MP1306 EUSpec. JM acknowledge also the CENTEM project (CZ.1.05/2.1.00/03.0088 co-funded by the ERDF).
Author information
Authors and Affiliations
Contributions
C.H. coordinated the project. H.C., L.C. and D.V. wrote the paper. H.C. developed the spectrometer and carried out the 2D-ACAR measurements together with J.W. Electronic structure calculations the spin-polarized 2D-ACAR spectra have been performed by D.B., L.C., J.M. and H.E. All authors discussed and contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Ceeh, H., Weber, J., Böni, P. et al. Local electron-electron interaction strength in ferromagnetic nickel determined by spin-polarized positron annihilation. Sci Rep 6, 20898 (2016). https://doi.org/10.1038/srep20898
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep20898
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

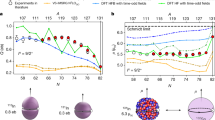



 is found for
is found for  eV. The inset shows the results for the 1D data. (The dotted lines act as a guide to the eye).
eV. The inset shows the results for the 1D data. (The dotted lines act as a guide to the eye).
