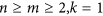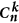Introduction

Large-scale quantum information processing (QIP) requires the generation, manipulation and measurement of fully coherent superposed quantum states involving many qubits1. A central issue for QIP is how well such a many-qubit system can maintain its quantum coherence. From the perspective of fundamental physics, an equally intriguing question that has been repeatedly asked is how a large number of microscopic quantum mechanical systems together behave classically as a macroscopic object2. To answer these questions, it is crucial to identify the key elements determining the scaling behavior of the decoherence of a multi-qubit system.

A confined single electron spin in a semiconductor quantum dot (QD) or a shallow donor is highly quantum coherent and is a promising candidate as a qubit3,4,5,6,7,8,9,10,11,12. It is now well understood that the main single-spin decoherence channel is through hyperfine coupling to the environmental nuclear spins10,12,13 and the effects of hyperfine interaction have been investigated for coupled two- and three-spin systems14,15,16,17,18,19,20,21,22. A many-spin-qubit system thus offers a convenient test ground for studying decoherence scaling since different factors in the overall decoherence can be easily distinguished.

The study of whether quantum coherent features of a many-qubit system can survive over long evolution times started with the discovery and exploration of the decoherence-free subspace (DFS)23,24,25,26,27, where the many qubits in a system share a common reservoir. The states in a DFS do not experience decoherence from the collective noise from the reservoir, while states outside the subspace do. The concept of DFS clearly illustrates an important difference between decoherence of a single qubit and that for many qubits: the decoherence of single-qubit is characterized by relaxation time T1 and dephasing time T2, irrespective of the qubit state; while with the many more density matrix elements involved, the decoherence of an n-qubit state is generally state-structure-dependent. This dependence is the main focus of the present work.

In this study we focus on the hyperfine-induced decoherence of n (≫1) uncoupled QD-confined electron spin qubits. Our goals are to clarify how decoherence of many-qubit states depends on the number of qubits and the state structure. In our study, a uniform magnetic field is applied to make the Zeeman splitting Ω much larger than the nuclear-spin-induced inhomogeneous broadening (see Fig. 1), so that spin relaxation is negligible. The dominant single-spin decoherence channel is pure dephasing due to the nuclear spins. We explore how this mechanism affects a many-spin-qubit state by systematically examining a large number of superposed states in various forms. Specifically, if the fidelity of an n-qubit state decays as exp[−γ(t)], we clarify how γ(t) depends on the qubit number n or the number of basis states m (which could be exponentially large as compared to n). Our results from this broad-ranged exploration indicate decoherence scaling behavior ranging from scale-free up to sublinear to n, making the scale-up of a spin-based quantum computer a tractable endeavor.

Figure 1
figure 1

The energy spectrum for n electron spins separately confined in n uncoupled QDs in a finite uniform magnetic field.

The spectrum splits into n + 1 Zeeman sub-levels. k refers to the number of spins that point down. Each electron spin is coupled to local nuclear spins through hyperfine interaction, which produces a local field in the order of ∆B, so that the energy level for each Zeeman manifold is broadened to a band with width .

Full size image

Electron-nuclear spin hyperfine interaction

We consider n uncoupled electron spins in a finite uniform magnetic field, each confined (in a quantum dot, nominally) and interacting with its own uncorrelated nuclear-spin bath through hyperfine interaction:

where is the nuclear Zeeman splitting of the α-th nuclear spin in the j-th QD (from here on j will always be used to label the QDs and the corresponding electron spin qubits) and Aja is the hyperfine coupling strength. The number of nuclear spins coupled to the j-th electron spin, Nj, is in the order of 105 to 106 in GaAs QDs and in natural Si QDs.

The total Hamiltonian (1) is a sum of n fully independent single-spin decoherence Hamiltonians. The evolution operator for these n qubit can thus be factored into a product of operators for individual qubits. We present a brief recap of single-spin decoherence13,28 properties in Method and focus here on the multi-spin-qubit decoherence problem. Recall that inhomogeneous broadening corresponds to stochastic phase diffusion of an electron spin due to longitudinal Overhauser field and is characterized by the time scale . On the other hand, the narrowed-state free induction decay is caused by fluctuations in the transverse Overhauser field and is characterized by the time scale T2. These two time scales are statistically independent because of independence between longitudinal and transverse Overhauser fields, as presented in Method. These two pure dephasing channels follow the same scaling law, i.e., , where n is the number of spin qubits in the system. Thus we can focus on the scaling analysis of either of them. In the following we employ to represent the result, which is applicable to both dephasing channels.

Results

Multi-spin decoherence

For an n-spin system in a finite uniform magnetic field, the full Hilbert space is divided into n+1 Zeeman subspaces, labeled by , . Each subspace consists of degenerate states (in the absence of nuclear field), which has k spins in the () state and spins in the state. The local random Overhauser fields break this degeneracy and lead to a broadening of the manifold (see Fig. 1). In all the following calculations, we use spin product states as the bases. Here refers to the electron spin orientation along the z-direction in the j-th QD for state and takes the value of or for notational simplicity.

For a superposed state containing more than one product state, decoherence emerges due to the non-stationary random phase differences among the m product states 's: with . The number of product states in , , is also the Hilbert space size of concern because spin relaxation is generally negligible in a finite field and is not considered in this study. We treat the Overhauser field (both longitudinal and transverse components) semiclassically, accurate to the second order in its magnitude. The notation represents a sum of Overhauser fields from every QD and is defined in Method. As a measure of decoherence of caused by the hyperfine interaction, we use fidelity , which can be simplified in the presence of dephasing as

where is the Overhauser field difference experienced by the two n-spin product states (see Method). Specifically, is solely determined by the number of spins that are opposite in orientation between bases and . Therefore, the fidelity depends on the structure of the interested state, i.e., the constituents and their weight in the superposed state and single-qubit decoherence is only one of several important ingredients in the multi-qubit decoherence problem.

Classification of multi-spin decoherence

With our understanding of single-spin decoherence and with fidelity of the collective decoherence for a multi-spin state defined, we are now in position to clarify multi-spin decoherence in various subspaces of the n-spin system.

Case A: single product state

The simplest multi-spin state is a single product state. The random Overhauser fields experienced by the spin qubits create a random but global phase (relative to when the nuclear reservoir is absent). This global phase does not lead to any decoherence, as there is no coherence (phase) information stored in any product state.

Case B: two product states, with m = 2 and k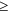

The simplest multi-spin state that can undergo dephasing consists of two product states. Here we choose a particular class of , with one state being fully polarized , while the other being from the k-th subspace with k spins in . The fidelity of this state is , so that

In this case, dephasing time is inversely proportional to the square root of the number of spins prepared as in . A special example here is the GHZ state, . The decoherence rate is , where the square root of the number of spin qubits is from the quadratic time dependence in the exponent of . The worst case scenario for an containing two product states is when they have completely opposite spins.

Case C: n ≥ m ≥ 2, k = 1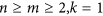

We now consider an that is a superposition of m product states from the manifold with one spin in . Explicitly, , where . This state is slightly more general than the well-known W state, with a random weight and phase for each basis state. The fidelity of is , which implies (by the CauchySchwarz inequality)

Here the upper bound ( means no decoherence) is approached when a particular product state dominates over all others in weight: while , so that we go back to Case A. The lower bound for decoherence time is scale-free with respect to n, when the whole system acts like a giant spin system in which the spin polarization is spread out over n physical spins. The lower bound corresponds to the equally-populated superposed states with , i.e., an almost standard W state (which would have all dj having the same phase, too). For a large number of qubits, , , where the scaling of decoherence is insensitive to either the population distribution on each basis state or the total number of physical spins.

Case D: m =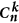

We now extend to a more generalized W-state that is distributed over all the product bases in the k-th Zeeman manifold, with . For a clear physical picture let us first consider a special example where all the product states have the same weight: with . The overall decoherence is determined by the phase differences between every pair of states from the basis states as well as the population distribution. Since , we limit our discussion below to without loss of generality. The phase difference between a particular pair of and can involve Overhauser fields in 2j QDs, where . In the extreme case of 2j = n, they have completely opposite spins. After a straightforward derivation via combinatorial mathematics, the fidelity for this state is found to be . Thus

In particular, (a) when while k is kept as a constant, , which is scale-free with respect to the number of spins n as well as the number of product states m in (it is a similar feature as in Case C with ); (b) overall decoherence is completely suppressed when or , i.e. . These two Zeeman manifolds contain one state each, so that Case D is reduced to Case A; (c) the strongest decoherence occurs when , where .

The generalized W state here is a reliable and tight lower bound for the decoherence scaling rate of a more general state in the k-th manifold where dr is an arbitrary number. In Fig. 2, the lines represent the analytical result given by Eq. (5) and the data points are obtained from 100 randomly generated states. The inset of the figure shows that the standard deviations in for the random states scale as a power-law function of m. More specifically, , when , , respectively. This m-dependence originates from the randomness we have introduced in the populations of the m states involved in each . With , the convergence of the calculated is extremely fast as we increase n, as indicated in Fig. 2. In short, Fig. 2 clearly indicates that the equal-weight state is a very good representative of the large class of states from both Cases C and D. Furthermore, while decoherence rate of generally scales as , the convergence rate scales as .

Figure 2
figure 2

vs. n for randomly generated states (with random populations over bases) in the -th Zeeman manifold in Case D.

The lines are generated from the analytical expression of Eq. (5) based on the state. Inset: standard deviation σ of obtained from 100 states, as a function of the Hilbert space size m.

Full size image

Case E: m = 2n

We now consider in the full Hilbert space of the n qubits. For the overall decoherence, pairs of phase differences have to be taken into account. The simplest such state is the fully and equally superposed state , which is the initial state employed by Shor’s algorithm of factorization29 and one-way computing30. Its fidelity is simply the product of single-qubit fidelity . Thus,

As in Case D, we can generalize to by randomizing the weight 's, . In Fig. 3 we plot our numerical results as compared with the analytical expression from Eq. (6). The size of error bars in Fig. 3 for random states rapidly vanishes with increasing n. Similar to Case D, the inset shows that the standard deviation of scales with the Hilbert space size m in the form . Since here m increases exponentially with n, the rapid suppression of error bar size as we increase n is not surprising. Consequently, the decoherence time for an arbitrary state adheres to the sublinear power-law as soon as .

Figure 3
figure 3

Average vs. n from randomly generated states over the whole Hilbert space of the n-spin system.

The solid line is generated by Eq. (6), using the equal-superposition state . Inset: standard deviation of vs. Hilbert space size m = 2n. For each n, The results are generated from 100 randomly selected states.

Full size image

Discussion

We have explored the scaling behavior of decoherence of n uncoupled electron spin qubits by investigating the fidelity of 5 classes of representative superposed states . Our results are summarized in Table 1, where k is the number of spins in in a product state that makes up of . Typically, the pure dephasing rates are not related to the sub-Hilbert-space size m. Instead, they are usually sublinear power-law functions of the qubit number n, with the exponent determined by the single-spin decoherence mechanism. Furthermore, if is constrained in a single subspace with a fixed k, and become scale-free with respect to n and m, in the spirit of DFS, though the noise sources here are not common to all qubits.

Table 1 A summary of decoherence times of n uncoupled electron spin qbits under the influence of hyperfine coupling with local nuclear baths.
Full size table

Fidelity is one specific way to represent the environmental decoherence effects on a multi-qubit state, with equally weighted contributions from all the off-diagonal density matrix elements. We choose it partially because there is no consensus measure for multi-qubit entanglement. Still, fidelity does provide hints on the robustness of certain entangled states against pure dephasing considered in this study. It should be noted that the results for the often-studied multipartite states, GHZ states and W states (presented in Cases B and C, respectively) coincide with their entanglement behaviors. The entanglement of W states (fidelity undergoes scale-free decay with respect to n) outperforms that of GHZ states (fidelity decay rate is proportional to ) in terms of their robustness31. The independence on n by the W states is generic, insensitive to the behavior of single-qubit decoherence.

The scalings revealed in our case studies can be qualitatively understood by counting the number of different spin orientations in any pair of product states. Among m product states making up an arbitrary state , a large fraction of pairs have electron spins oriented in the opposite direction. If we average over all possible states assuming , the fidelity given by Eq. (2) could be estimated as . The decoherence rates are insensitive to m because of normalization and our equal-population assumption. More specifically, in the k-th manifold, the scaling law is because any pair of states here is different at most in spins. This scale-free behavior (with respect to n and m) is quite generic26,27 and not dependent on single-qubit decoherence.

Our study here could be straightforwardly extended to other single-qubit decoherence mechanisms. In general, if the single-spin decoherence function is given by , the index of every power-law () in Table 1 should be changed to . For decoherence due to Gaussian noise under dynamical decoupling32, the decay functions have for spin echo and for two-pulse Carr-Purcell-Meiboom-Gill sequence, so that the decoherence scaling factors for the n-spin system become and , respectively. For spin relaxation induced by electron-phonon interaction that produces a linear exponential decay characterized by T1, the sub-Hilbert space spanned by a multi-qubit state is usually not fixed. So that a comprehensive understanding of the decay scaling power-laws requires further studies. Nevertheless, certain coherence terms in the n-spin system will still follow scaling, same as what our dephasing study indicates.

Generally, decoherence of any class of multi-qubit states is independent of the Hilbert space size m. Whether it is scale-free or scales as a polynomial of n depends on the state-structure, while the specific power-law depends on the single-qubit decoherence mechanism. On the other hand, the variability of decoherence for arbitrary states decreases polynomially with increasing m because we only consider dephasing.

In conclusion, we find that the structure of a multi-qubit state is a critical ingredient in determining its collective decoherence. While different from DFS33, the scale-free states help identify Hilbert subspaces that are more favorable in coherence preservation for spin-based qubits under the influence of local nuclear spin reservoirs.

Method

Single-Spin Decoherence

For a single electron spin coupled to the surrounding nuclear spins in a finite magnetic field, the nuclear reservoir causes pure dephasing via the effective Hamiltonian13,28

where N is the number of nuclear spins, Ω is the electron Zeeman splitting and Aα is the hyperfine coupling strength. The sums over α and here are over all the nuclear spins in the single quantum dot (QD). The dephasing dynamics has two contributions: HA is the longitudinal Overhauser field, while V is the second-order contribution from the transverse Overhauser field. In a finite field, normally the former dominates, generating a random effective magnetic field of mT9 on a quantum-dot-confined electron spin in GaAs. This random field leads to a stochastic phase and accounts for the inhomogeneous broadening effect characterized by a free induction decay at the time scale of , where 1 indicates that only one electron spin is considered. For this single spin, the inhomogeneous broadening decoherence function is:

Here is an ensemble average over the longitudinal Overhauser field in the QD and with . In a single gated QD in GaAs, is in the order of 10 ns.

If the effect of HA is suppressed, such as through nuclear spin pumping and polarization10, V, which is second order in the transverse Overhauser field, leads to the so-called narrowed-state free induction decay, by which the off-diagonal elements of the spin density matrix decay at the time scale of . In the manuscript and here we will simplify the notation for to , where n indicates the number of spin qubits in consideration. For a single spin, n = 1 and the narrowed-state decoherence function is given by:

where 13 and is in the order of μs in a gated GaAs QD.

Notations on the multi-quantum-dot Overhauser fields

A convenient way to understand the effect of hyperfine interaction on the n-uncoupled-qubit system [see Eq. (1)] is to introduce the semiclassical Overhauser field: , where refers to the longitudinal and transverse directions, lj takes the value of 1 or and is the Overhauser field in the j th QD. In a finite field and up to second order, the hyperfine Hamiltonian could be diagonalized on the product state basis into

where

Here () if (). The two terms in Eq. (11) are responsible for the inhomogeneous broadening and narrowed-state FID, respectively. Accurate to the first order in , , since is second order in the hyperfine coupling strength and is small. For simplicity we take in the following derivation. Generally, the second-order term for the j th dot in Eq. (11) . For example, a completely polarized state experiences a longitudinal Overhauser field . Thus our work is accurate to the second order of the hyperfine coupling. In the main text, the Overhauser fields are treated semiclassically, with the field operators replaced by c-numbers.

With the hyperfine Hamiltonian takes on a diagonal form, it only leads to dephasing between different product states due to , similar to the single-spin case we discussed above. The dephasing of a product state relative to is due to the difference in the random Overhauser field for these states.

Statistical independence of inhomogeneous broadening and narrowed-state free induction decay

To analyze the relationship between inhomogeneous broadening from the longitudinal Overhauser field and narrowed-state free induction decay due to the transverse Overhauser field in an n-uncoupled-qubit system, we consider an arbitrary pure state in a subspace spanned by m spin product states , where . Here refers to the electron spin orientation along the z-direction in the j th QD for state and takes the value of 1 or for notational simplicity. The whole Hilbert space of the n-qubit system could be divided to manifolds according to the number of for the product bases, as indicated in Fig 1. The choice of here is sufficiently general to cover all the cases discussed in the manuscript. Helped by the Overhauser fields defined above and under the diagonalized hyperfine interaction Hamiltonian in Eq. (10), an initial state evolves into

where is the Overhauser field experienced by the product state . Decoherence of emerges due to the non-stationary random phase differences from these Overhauser fields. The fidelity between and can be expressed as

where the phase differences .

According to Eq. (11), each could be decomposed into two terms, and , that are responsible for the inhomogeneous broadening and narrow-state free induction decay, respectively:

The ensemble average could be estimated using the decoherence times of a single qubit system (inhomogeneous broadening time scale) and (the narrowed-state FID time scale)13,

This result is obtained using the canonical approach to treat quantum noise34 and is valid at least in the short time limit. Physically it is based on the assumption that longitudinal and transverse Overhauser fields are independent from each other, so that the averages above can be factored. The two decoherence mechanisms are thus mutually independent. Using the short notations , and , Eq. (14) can be rewritten as

where . In short, Eqs (15) and (16) show that inhomogeneous broadening and narrowed-state FID are independent decoherence channels and have the same scaling behavior. The overall decoherence function is just a simple product of the decay functions for inhomogeneous broadening FID and narrowed-state FID. We can thus focus on calculating in our discussion of decoherence scaling for n spin qubits.

For a simple example, take . The inhomogeneous broadening part in Eq. (16) then takes on the form , where . After a semiclassical evaluation of the Overhauser field noise34 and using the expressions of in Eq. (8) and in Eq. (9), we find , so that in the short-time limit. Therefore, in this example, .

Additional Information

How to cite this article: Jing, J. and Hu, X. Scaling of decoherence for a system of uncoupled spin qubits. Sci. Rep. 5, 17013; doi: 10.1038/srep17013 (2015).