Abstract
Semi-device-independent random number expansion (SDI-RNE) protocols require some truly random numbers to generate fresh ones, with making no assumptions on the internal working of quantum devices except for the dimension of the Hilbert space. The generated randomness is certified by non-classical correlation in the prepare-and-measure test. Until now, the analytical relations between the amount of the generated randomness and the degree of non-classical correlation, which are crucial for evaluating the security of SDI-RNE protocols, are not clear under both the ideal condition and the practical one. In the paper, first, we give the analytical relation between the above two factors under the ideal condition. As well, we derive the analytical relation under the practical conditions, where devices’ behavior is not independent and identical in each round and there exists deviation in estimating the non-classical behavior of devices. Furthermore, we choose a different randomness extractor (i.e., two-universal random function) and give the security proof.
Similar content being viewed by others
Introduction
Truly random numbers have been wildly applied in many aspects such as numerical simulations of physical and biological systems, gambling and cryptography. As we know, the security of quantum key distribution (QKD) protocols depends on random selections of the prepared states and measurements so that adversary cannot utilize an attack to get secret information without being discovered.
There is no intrinsic randomness in the world of classical physics. In principle, any classical system admits a perfect description. And any observed randomness of a classical process is apparent (called as apparent randomness1), since it can be explained as the probabilistic mixture of deterministic classical events. Specially, the existing random number generators such as the linear feedback shift registers, which are characterized by using the deterministic algorithms, generate apparent randomness for us due to lacking of knowledge about their precise descriptions.
The advent of quantum physics makes it possible to produce intrinsic randomness. Colbeck et al.2 gave a RNE protocol based on Greenberger-Horne-Zeilinger (GHZ) paradox. Pironio et al.3 proposed a RNE protocol, where the generated randomness was certified by non-local correlation in the Clauser-Horn-Shimony-Holt (CHSH) test and quantified by min-entropy4,5,6 of measurement outcomes. Fehr et al.7 further characterized the amount of the generated randomness based on the ref. 3 and proposed a superpolynomial RNE protocol. Pironio et al.8 analyzed that honest and dishonest device suppliers had influence on RNE and optimized conclusions of the ref. 3. The above protocols are categorized as DI-RNE ones, which make no assumption about the internal working of the devices.
As is well-known, DI-RNE protocols require entanglement, which results in negative effects on the complexity of devices and the rate of randomness generation. Thus the question whether we can generate randomness without any entanglement may arise. Fortunately, Li et al.9 proposed SDI-RNE protocols without entanglement based on 2 → 1 quantum random access code (QRAC)10,11 and the generated randomness was certified by non-classical correlation in the prepare-and-measure test. Furthermore, Li et al.12 generalized the case of the ref. 9 to more general ones (i.e., n → 1 QRAC) and pointed out 3 → 1 QRAC was the most efficient SDI-RNE protocols. These SDI-RNE protocols, where the users have no knowledge of internal working of the devices except for the dimension of the systems, are preferred since they are convenient for application.
The security of RNE protocols is of importance. As the security of QKD protocols13,14,15,16 emphasizes key rate, the security of RNE ones focuses on the amount of the generated randomness. In the above mentioned DI-RNE protocols, the analytical relations between the amount of the generated randomness and Bell inequality violation was presented under the ideal and practical conditions3,7,8. And in the SDI scenario, the relation between the amount of the generated randomness and the degree of non-classical correlation was given by using Levenberg-Marquadrt (L-M) algorithm9,12 and semi-definite programm (SDP) relaxation17,18,19 under the ideal condition, respectively.
There are some problems worth thinking about in the SDI-RNE protocols. The analytical relation between the amount of the generated randomness and the degree of non-classical correlation under the ideal condition is missing. In practice, the behavior of the device is not identical and independent in each round and there exists deviation in estimating the non-classical behavior of the devices. It is natural to ask that the amount of the generated randomness and the degree of non-classical correlation satisfy what kind of analytical relation considering the above practical conditions.
In the paper, we give the analytical relation between the amount of the generated randomness and the degree of non-classical correlation under the ideal condition. Furthermore, we consider the practical conditions and establish the analytical relation which is described by a lower bound on the amount of the generated randomness based on the non-classical behavior of the devices. Finally, we choose two-universal random function20 as randomness extractor and give the security proof.
Results
The model of SDI-RNE protocols12
Suppose that the relevant dimension d of the quantum systems are- known, in this work we take d = 2. But the prepared states and measurement are not described. Generally, Alice’s and Bob’s black boxes are systems for state preparation  and measurement
and measurement  . Alice chooses n bits x = x0x1... xn−1 ∈ {0, 1}n at random and sends the encoded state
. Alice chooses n bits x = x0x1... xn−1 ∈ {0, 1}n at random and sends the encoded state  to Bob. Then Bob chooses a measurement operator
to Bob. Then Bob chooses a measurement operator  acting on the state ρx with input parameter y ∈ {0, 1,..., n − 1} and output parameter b ∈ {0, 1}, where
acting on the state ρx with input parameter y ∈ {0, 1,..., n − 1} and output parameter b ∈ {0, 1}, where  ,
,  . After repeating the procedure infinite times, Alice and Bob can get the probability distribution
. After repeating the procedure infinite times, Alice and Bob can get the probability distribution  . The generated randomness can be certified by the non-classical correlation.
. The generated randomness can be certified by the non-classical correlation.
Denote

called as  expression. If the systems admit a classical description, then
expression. If the systems admit a classical description, then  expression based on 2 → 1 QRAC satisfies
expression based on 2 → 1 QRAC satisfies  , denoted as
, denoted as  simply. Obviously, if the systems contain the non-classical correlation (i.e., certain measurements act on quantum states), the data can violate the above inequality and makes
simply. Obviously, if the systems contain the non-classical correlation (i.e., certain measurements act on quantum states), the data can violate the above inequality and makes  expression value up to
expression value up to 
 . Similarly,
. Similarly,  expression based on 3 → 1 QRAC satisfy
expression based on 3 → 1 QRAC satisfy  .
.
The amount of randomness of output b conditioned on the inputs x, y can be characterized by the min-entropy4

where the maximal guessing probability4 of B given X, Y is

Based on equation (2), exploring a lower bound on min-entropy is equivalent to the upper bound on maximal guessing probability. So, to calculate the amount of the generated randomness can be converted into exploring maximal guessing probability for given value of  expression in the following optimization problem.
expression in the following optimization problem.

subject to:


where the optimization is carried out by arbitrary quantum state ρx and positive operator valued measure (POVM)  defined over two dimensional Hilbert space.
defined over two dimensional Hilbert space.
Analytical relation under the ideal condition
We give the analytical relation between the maximal guessing probability and the corresponding maximal value of  expression. Moreover, we get the explicit bounds of
expression. Moreover, we get the explicit bounds of  expression when there is the generated randomness. In other words, we gain the reason why there is not the generated randomness when the data just violates the classical bound of
expression when there is the generated randomness. In other words, we gain the reason why there is not the generated randomness when the data just violates the classical bound of  expression. Here, we mainly give the results of the primitive ones (proved in the Supplementary Information).
expression. Here, we mainly give the results of the primitive ones (proved in the Supplementary Information).
Theorem 1. Suppose that SDI-RNE protocol based on 2 → 1 QRAC is associated with two dimensional Hilbert space. The analytical relation between the maximal guessing probability p and the corresponding maximal value of  expression is given as
expression is given as

where
 and r is one of the real roots of equation
(8)
with a variable x
and r is one of the real roots of equation
(8)
with a variable x

According to the analytical relation (7), denoted as  , we explore the critical value of
, we explore the critical value of  expression conditioned on there exists the generated randomness. Let p = 1 (i.e., there is not the generated randomness of the outputs), we get
expression conditioned on there exists the generated randomness. Let p = 1 (i.e., there is not the generated randomness of the outputs), we get  (r = 0.7904) by taking over all the real roots of the equation expressed as 4x4 + 4x3 + x2 − 4x − 1 = 0. Further, we learn that g1 is the monotonically decreasing and continuous function. As long as
(r = 0.7904) by taking over all the real roots of the equation expressed as 4x4 + 4x3 + x2 − 4x − 1 = 0. Further, we learn that g1 is the monotonically decreasing and continuous function. As long as  , the outputs exhibit randomness (p < 1).
, the outputs exhibit randomness (p < 1).
Theorem 2. Suppose that SDI-RNE protocol based on 3 → 1 QRAC is associated with two dimensional Hilbert space. The analytical relation between the maximal guessing probability p and the corresponding maximal value of  expression is given as
expression is given as

where  and the values of (r, s, v, m) is one of the real roots of the equation set in variables (x, y, z, u) in the Supplementary Information.
and the values of (r, s, v, m) is one of the real roots of the equation set in variables (x, y, z, u) in the Supplementary Information.
Similar to the above analysis, we calculate the critical value of  expression conditioned on there exists the generated randomness. Let p = 1, we get
expression conditioned on there exists the generated randomness. Let p = 1, we get  ((r, s, v, m) = (0.7730, 0.3837, −0.1529, 1)) by taking over all the real roots of the equation set in the Supplementary Information. So, we conclude that as long as
((r, s, v, m) = (0.7730, 0.3837, −0.1529, 1)) by taking over all the real roots of the equation set in the Supplementary Information. So, we conclude that as long as  , the generated randomness can be certified.
, the generated randomness can be certified.
Analytical relation under the practical condition
In practice, there exist some unideal factors during the experiment, for example, the behavior of the devices is not identical and independent in each round and estimating the non-classical behavior of the devices causes deviation. We establish the analytical relation between the amount of the generated randomness and the degree of non-classical correlation under the practical condition. As well, our result can be applied to any RNE protocols with quantum system of arbitrary dimension and a general form of  expression in the SDI scenario.
expression in the SDI scenario.
Description of the devices used t times in succession
We consider a pair of devices  , where the state preparation
, where the state preparation  and measurement
and measurement  can be regarded as two black boxes. The preparation box contains a set of arbitrary states
can be regarded as two black boxes. The preparation box contains a set of arbitrary states  and the measurement box contains a sequence of arbitrary measurements
and the measurement box contains a sequence of arbitrary measurements  defined over two-dimensional Hilbert space, where measurement operator
defined over two-dimensional Hilbert space, where measurement operator  represents input parameter yi and output parameter bi.
represents input parameter yi and output parameter bi.
We make the most basic assumptions as follows:
-
1
the preparation system and the measurement system conform to the quantum theory;
-
2
there is no additional communication between the state preparation system and the measurement system in each round. That is, the state preparation system and the measurement system have a single qubit for communication and are not allowed to divulge information to eavesdropper in each round;
-
3
the inputs X, Y are random variables that are independent and uncorrelated with the devices.
No constrains are imposed on the states and measurements except for their dimension and the above assumptions. But the behavior of devices is not identical and independent in each round i, which implies that the previous i − 1 states, measurement operators and measurement outcomes affect the ith measurement outcomes. Note that we assume that the state preparation system are not entangled with the measurement system or any other party in the following calculation of the amount of generated randomness, which is similar to that in previous work7,8.
We denote the inputs by xi ∈ X, yi ∈ Y and the measurement output by bi ∈ B in the ith round. We denote the first i inputs by xi = (x1, x2,..., xi) and define yi, bi similarly. The devices’ behavior cannot be identical and independent in each round. That is, the behavior of devices varies from one round to another making use of internal memory, which is depicted by a sequence of unitrary transformations U0,..., Ut−1 acting on  . Ui−1 is used for the state and the measurement operator before the ith round (U0 = I in the first round). In details, suppose that Alice chooses the state
. Ui−1 is used for the state and the measurement operator before the ith round (U0 = I in the first round). In details, suppose that Alice chooses the state  at will and Bob chooses the measurement setting
at will and Bob chooses the measurement setting  in the first round, we get
in the first round, we get  . Alice and Bob choose
. Alice and Bob choose  at random, due to un-identical and dependent between rounds, we get
at random, due to un-identical and dependent between rounds, we get  , where the operation U1 encodes the information of the inputs x1, y1 and output b1 in the first round. The given conditional probability distribution
, where the operation U1 encodes the information of the inputs x1, y1 and output b1 in the first round. The given conditional probability distribution  , which describes the input-output behavior of t sequential interactions with the devices
, which describes the input-output behavior of t sequential interactions with the devices  &
&  , is defined as
, is defined as

where  . The first equality holds because of successive Bayes’ principle and the second one shows that the output in the ith round is determined by the inputs of the ith round and the pervious inputs and outputs.
. The first equality holds because of successive Bayes’ principle and the second one shows that the output in the ith round is determined by the inputs of the ith round and the pervious inputs and outputs.
We learn that there is one-to-one correspondence between the maximal guessing probability and the corresponding maximal value of  expression based on the analytical relations (i.e., collectively called g1) in the above part. The analytical relations show
expression based on the analytical relations (i.e., collectively called g1) in the above part. The analytical relations show

where g1 is the monotonically decreasing and continuous function of the corresponding maximal value of  and
and  is the convex function of the value of
is the convex function of the value of  expression.
expression.
Estimating the degree of non-classical correlation
Here, we estimate  expression value to characterize the degree of non-classical correlation.
expression value to characterize the degree of non-classical correlation.
For the first round,  expression value is established by
expression value is established by  . For other rounds, there are slightly different because of the present round depending on the inputs and outputs of the previous rounds. So,
. For other rounds, there are slightly different because of the present round depending on the inputs and outputs of the previous rounds. So,  expression value in the ith round is
expression value in the ith round is  .
.
Let

be the average value of  expression, averaged over t rounds. In order to estimate the average value
expression, averaged over t rounds. In order to estimate the average value  , we introduce the following estimator
, we introduce the following estimator  , determined from the observed statistics:
, determined from the observed statistics:

where  is the observed value of
is the observed value of  expression in the ith round and χ(x) is the indictor function:
expression in the ith round and χ(x) is the indictor function:

We derive the result of estimating the average value  in the following (proved in the Supplementary Information).
in the following (proved in the Supplementary Information).
Lemma 3. Let the symbols be the same as before. For any δ > 0, the average value  and the observed average value
and the observed average value  satisfy
satisfy

where  , αmax = max|{αb,x,y}|, Pmin = min{P(x)P(y)} and WQ is the maximal value of
, αmax = max|{αb,x,y}|, Pmin = min{P(x)P(y)} and WQ is the maximal value of  expression allowed by quantum theory.
expression allowed by quantum theory.
From inequality (15), we learn that the average value  can be larger than the observed average value
can be larger than the observed average value  up to some δ with probability 1 when experiment’s rounds tend toward infinity.
up to some δ with probability 1 when experiment’s rounds tend toward infinity.
Bounding the min-entropy
Here, we proceed with the last step to get the analytical relation between the amount of the generated randomness and the observed average value  under the practical conditions. Just as the refs 7, 8 consider the average Bell value in some interval as a prior condition to make the min-entropy meaningful in the DI case, we use the technique7 to quantify the generated randomness, which is depicted by a lower bound on min-entropy of outputs conditioned on the event that the observed average value
under the practical conditions. Just as the refs 7, 8 consider the average Bell value in some interval as a prior condition to make the min-entropy meaningful in the DI case, we use the technique7 to quantify the generated randomness, which is depicted by a lower bound on min-entropy of outputs conditioned on the event that the observed average value  lies in some interval.
lies in some interval.
Denote W0 by the maximal value of  expression conditioned on Hmin(Bt|XtYt) = 0. W0 > Wcl (the classical bound of
expression conditioned on Hmin(Bt|XtYt) = 0. W0 > Wcl (the classical bound of  expression), which is different from that of Bell experiments. We partition the interval [W0, WQ] ⊂ R into
expression), which is different from that of Bell experiments. We partition the interval [W0, WQ] ⊂ R into  disjoint blocks:
disjoint blocks:  with Φl = [Wl−1, Wl).
with Φl = [Wl−1, Wl).
Here, a basic event space  is the set that includes all possible (bt, xt, yt, l) for the above experiment. Define an event
is the set that includes all possible (bt, xt, yt, l) for the above experiment. Define an event  . According to Lemma 3, the event
. According to Lemma 3, the event  occurs with high probability. In fact, the values of (bt, xt, yt) can determine the value of
occurs with high probability. In fact, the values of (bt, xt, yt) can determine the value of  and random variable l. Next, we define an event
and random variable l. Next, we define an event  and an event
and an event  . Let
. Let  be the good event, denoted as
be the good event, denoted as  . We call
. We call  as the good event (i.e.,
as the good event (i.e.,  ) since we can get the amount of the generated randomness as long as all of the events
) since we can get the amount of the generated randomness as long as all of the events  and
and  occur. Note that an event is a set that contains one or more results of a basic event space, which is a subset of the basic event space. As well, each result of an event is a element (basic event).
occur. Note that an event is a set that contains one or more results of a basic event space, which is a subset of the basic event space. As well, each result of an event is a element (basic event).
The following lemma is proven in the Supplementary Information.
Lemma 4. There exist the above good event  with probability
with probability

We try to put a bound on the min-entropy of the outputs Bt conditioned on the inputs (Xt, Yt) and the observed average value  in some interval.
in some interval.
Theorem 5. Let (X, Y) be identical, independent and random sources and δ > 0 be an arbitrary parameter. For any devices’ behavior, the observed distribution P = {P(bt, xt, yt)} characterizing successive t rounds satisfies

for all

Proof. Without loss of generality, suppose that l is the unique value with  .
.
Let  , we consider nontrivial cases, i.e.,
, we consider nontrivial cases, i.e.,  . Otherwise,
. Otherwise,  .
.
According to the description of  , we get
, we get

where the penultimate inequality holds because of  and the last one holds by using equations (10), (11) and (12).
and the last one holds by using equations (10), (11) and (12).
Furthermore, with the above inequality, it is easy to show that

Here, suppose that disjoint blocks  , δ = 0.0001 and the experiment’s rounds t = 1000, 4000, respectively. Under the ideal and practical conditions, we compare the lower bound on min-entropy of the generated randomness of SDI-RNE protocols based on 2 → 1 and 3 → 1 QRACs in Figs 1 and 2, respectively. Obviously, when rounds of experiments is increasing and the number of the disjoint blocks is fixed, the Figures reveal that the gap of the amount of the generated randomness between the ideal and practical conditions is rapidly closing. Note that W in the Figures represents the observed average value.
, δ = 0.0001 and the experiment’s rounds t = 1000, 4000, respectively. Under the ideal and practical conditions, we compare the lower bound on min-entropy of the generated randomness of SDI-RNE protocols based on 2 → 1 and 3 → 1 QRACs in Figs 1 and 2, respectively. Obviously, when rounds of experiments is increasing and the number of the disjoint blocks is fixed, the Figures reveal that the gap of the amount of the generated randomness between the ideal and practical conditions is rapidly closing. Note that W in the Figures represents the observed average value.
Randomness extraction
As we know, by using a randomness extractor20,21, the outputs bt can be converted to a string that is nearly uniform and uncorrelated to the information of an adversary.
We propose a SDI-RNE protocol with another randomness extractor which is different from ones of the refs 7, 8. The users ask providers for two devices, where state preparation  has 2n settings and measurement
has 2n settings and measurement  has n settings and can make two possible output 0, 1. Furthermore, the users ask that these devices satisfy the most basic assumptions. But, they have no knowledge of the internal working of devices except for their dimension. The protocol is presented in the following.
has n settings and can make two possible output 0, 1. Furthermore, the users ask that these devices satisfy the most basic assumptions. But, they have no knowledge of the internal working of devices except for their dimension. The protocol is presented in the following.
The users allow a single qubit to communicate in each round and do not send any information outside the laboratory.
-
1
Divide their initial truly random string
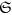 into S1 and S.
into S1 and S. -
2
Introduce (xi, yi) ∈ S1 into the devices and obtain output bi.
-
3
Repeat step (2) until exhausting S1 and build a output string.
-
4
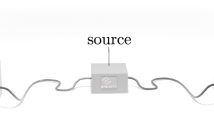
Calculate the observed average value and determine the value l that
 . If
. If  , the protocol aborts.
, the protocol aborts. -
5
Make use of S to choose the two-universal random function f and obtain a finial string. Based on Theorem 5, the length of the finial string is

In order to prove security of the proposed protocols, we make the lemma for preparation (proved in the Supplementary Information).
Lemma 6. Suppose that  is the two-universal random function22 and
is the two-universal random function22 and  , where bt ∈ {0, 1}t. We get
, where bt ∈ {0, 1}t. We get

Theorem 7. The proposed SDI-RNE protocol is  secure. That is, it is
secure. That is, it is  indistinguishable from a ideal protocol.
indistinguishable from a ideal protocol.
Proof. Based on the definition of security of protocol, we get

The penultimate inequality holds by using by the above Lemma 6.
Discussion
In the paper, we have showed the analytical relations between the amount of the generated randomness and the degree of non-classical correlation under the ideal and practical conditions. As a byproduct, the critical values of  expression have been presented when there exists the generated randomness. Moreover, the case, where the adversary holds the classical side information8 of the devices, can be regarded as our case conditioned on the particular value of the side information. Finally, we choose the two-universal function as randomness extraction and give the security proof. Whereas, there are still interesting questions that remain open. How can we quantify the generated randomness by directly using the observed probability distribution. Furthermore, for a given observed probability distribution, whether and how to find an optimal witness of given dimension with the method in the refs 19.
expression have been presented when there exists the generated randomness. Moreover, the case, where the adversary holds the classical side information8 of the devices, can be regarded as our case conditioned on the particular value of the side information. Finally, we choose the two-universal function as randomness extraction and give the security proof. Whereas, there are still interesting questions that remain open. How can we quantify the generated randomness by directly using the observed probability distribution. Furthermore, for a given observed probability distribution, whether and how to find an optimal witness of given dimension with the method in the refs 19.
Additional Information
How to cite this article: Li, D.-D. et al. Security of Semi-Device-Independent Random Number Expansion Protocols. Sci. Rep. 5, 15543; doi: 10.1038/srep15543 (2015).
References
Dhara, C., De La Torre, G. & Acn, A. Can observed randomness be certified to be fully intrinsic. Phys. Rev. Lett. 112, 100402 (2014).
Colbeck, R. & Kent, A. Private randomness expansion with untrusted devices. J. Phys. A: Math. Theor. 44, 095305 (2011).
Pironio, S. et al. Random numbers certified by Bell’s theorem. Nature (London) 464, 1021 (2010).
Köenig, R., Renner, R. & Schaffner, C. The operational meaning of min and max-entropy. IEEE Trans. Inf. Theory 55, 4337–4347, (2009).
Tomamichel, M., Colbeck, R. & Renner, R. Duality between smooth min and max-entropies. IEEE Trans. Inf. Theory 56, 4674–4681 (2010).
Köning, R. & Renner, R. Sampling of min-entropy relative to quantum konwledge. IEEE Trans. Inf. Theory 57, 4760–4787 (2011).
Fehr, S., Gelles, R. & Schaffner, C. Security and composability of randomness expansion from Bell inequalities. Phys. Rev. A 87, 012335 (2013).
Pironio, S. & Massar, S. Security of practical private randomness generation. Phys. Rev. A 87, 012336 (2013).
Li, H. W. et al. Semi-device-independent random-number expansion without entanglement. Phys. Rev. A 84, 034301 (2011).
Ambainis, A., Leung, D., Manciska, L. & Ozols, M. Quantum random access codes with shared randomness. e-print arXiv:quant-ph/0810.2937v3.
Pawłowski, M. & Éukowski, M. Entanglement-assisted random access codes. Phys. Rev. A 81, 042326 (2010).
Li, H. W., Pawłowski, M., Yin, Z. Q., Guo, G. C. & Han, Z. F. Semi-device-independent randomness certification using n → 1 quantum random acess codes. Phys. Rev. A 85, 052308 (2012).
Acn, A. et al. Device-independent security of quantum cryprography against collective attacks. Phys. Rev. Lett. 98, 230501 (2007).
Christandle, M., Renner, R. & Ekert, A. A generic security proof for quantum key distribution. e-print arXiv: quant-ph/0402131.
Masanes, S., Pironio, S. & Acn, A. Security device-independent quantum key distribution with causally independent measurement devices. Nature Commun. 2, 238–251 (2011).
Masanes, L., Renner, R., Christandl, M., Winter, A. & Barrett, J. Full security of quantum key distribution from no-signalling contraints. IEEE Trans. Inf. Theory 60, 4973–4986 (2014).
Li, H. W. et al. Relation between semi- and fully-device-independent protocols. Phys. Rev. A 87, 020302(R) (2013).
Mironowicz, P., Li, H. W. & Pawłowski, M. Properties of dimension witnesses and their semidefinite programming relaxations. Phys. Rev. A. 90, 022322 (2014).
Navascués, M. & Vértesi, T. Bounding the set of finite dimensional quantum correlations. Phys. Rev. Lett. 115, 020501 (2015).
De, A., Portmann, C., Vidick, T. & Renner, R. Trevisan’s ertractor in the presence of quantum side information. e-print arXiv: quant-ph/0912.5514v3.
Aroya, A. B. & Shma, A. T. Better short-seed quantum-proof extractors. Theoretical Computer Science 419, 17–25 (2012).
Bennett, C. H., Brassard, G., Crepeau, C. & Maurer, U. M. Generalized privacy amplification. IEEE Trans. Inf. Theory 41, 1915–1923 (1995).
Acknowledgements
This work is supported by NSFC (Grant Nos. 61272057, 61170270), Beijing Higher Education Young Elite Teacher Project (Grant Nos. YETP0475, YETP0477).
Author information
Authors and Affiliations
Contributions
D.L., Q.W., Y.W. and Y.Z. analyzed the previous DI-RNE and SDI-RNE protocols. Y.Z. and D.L. derived the analytical relation, F.G., D.L. and Y.W. analyzed other aspects, wrote the main manuscript text and prepared all figures. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Li, DD., Wen, QY., Wang, YK. et al. Security of Semi-Device-Independent Random Number Expansion Protocols. Sci Rep 5, 15543 (2015). https://doi.org/10.1038/srep15543
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep15543
This article is cited by
-
Expanding the sharpness parameter area based on sequential \(3{\rightarrow }1\) parity-oblivious quantum random access code
Quantum Information Processing (2023)
-
Semi-device-independent randomness expansion using \(n\rightarrow 1\) sequential quantum random access codes
Quantum Information Processing (2021)
-
The critical detection efficiency for closing the detection loophole of some modified Bell inequalities
Quantum Information Processing (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.




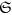 into S1 and S.
into S1 and S. . If
. If 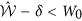 , the protocol aborts.
, the protocol aborts.