Abstract
The highly robust control of cell cycles in eukaryotes enables cells to undergo strictly ordered G1/S/G2/M phases and respond adaptively to regulatory signals; however the nature of the robustness remains obscure. Specifically, it is unclear whether events of signaling should be strictly ordered and whether some events are more robust than others. To quantitatively address the two questions, we have developed a novel cell cycle model upon experimental observations. It contains positive and negative E2F proteins and two Cdk inhibitors and is parameterized, for the first time, to generate not only oscillating protein concentrations but also periodic signaling events. Events and their orders reconstructed under varied conditions indicate that proteolysis of cyclins and Cdk complexes by APC and Skp2 occurs highly robustly in a strict order, but many other events are either dispensable or can occur in flexible orders. These results suggest that strictly ordered proteolytic events are essential for irreversible cell cycle progression and the robustness of cell cycles copes with flexible orders of signaling events and unveil a new and important dimension to the robustness of cell cycle control in particular and to biological signaling in general.
Similar content being viewed by others
Introduction
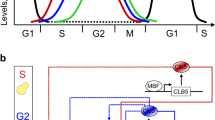
In the past decades experimental and computational biologists have tried to unveil the properties and control mechanisms of robust molecular signaling that are believed to be functionally important. The robustness of cell cycle control system in eukaryotic cells, due to its periodic activity and biological importance, has been intensively investigated. Most eukaryotic cells undergo four phases to finish a round of division. When growth factors drive a cell to enter into the G1 phase and pass through the restriction point (a point beyond which mitosis completion is ensured independently of the presence of growth factors), progression of the following S, G2 and M phases is controlled by the sequential activation of a family of cyclin/Cdk complexes (abbreviations shown in Fig. 1B are used hereafter and italics beginning with a normal letter designate genes). In 1989, Hartwell and Weinert expressed that “The events of the cell cycle of most organisms are ordered into dependent pathways in which the initiation of late events is dependent on the completion of early events”1. This viewpoint stresses the importance of the order of signaling events for the robust control of cell cycles. However, so far in all experimental and computational investigations robustness is evaluated by examining if concentrations of targeted molecules in a cell or a mathematical model are sensitive to perturbations or parameters. This method bears two drawbacks. First, signaling happens in diverse contexts and molecular responses to perturbations and parameters may reveal more about adaptiveness than robustness of the control mechanisms. Second, both protein concentrations and model parameters (such as binding affinity) are difficult to be accurately measured in experiments, leaving the order of and dependency between, events still unclear. While Hartwell and Weinert defined that “control mechanisms enforcing dependency in the cell cycle are here called checkpoints”, it remains unknown whether the dependency is enforced by merely checkpoints or also by other events. In brief, the nature of the robustness of cell cycle control is still inadequately understood.
The cell cycle model and definition of events.
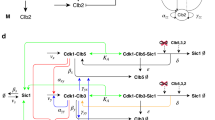
(A) Molecular interactions. The left panel shows protein interactions indicated by numbered links. Specifically, E2F1 in mammals is phosphorylated by CDKE and CDKB20 and CDKA60,61 for degradation, but in Drosophila is specifically destructed by CRL4Cdt2 periodically62,47. How CRL4Cdt2 is down-regulated after S phase is unclear63. Recent studies reveal that Cdt2 in CRL4Cdt2 is degraded by SCFFbxo11 and this degradation is prevented by phosphorylation of Cdt2 by CDKs64. Thus CDKs’ roles in preventing Cdt2 degradation may promote E2F1 destruction by CRL4Cdt2, agreeing with the initial observation that CDKs mediate E2F1 destruction. Directly or indirectly, we let CDKs mediate E2F1 degradation. Proteins with the symbol ^ indicate that they have a constant synthesis rate. Solid red and brown links ending with an arrow or a dot indicate activation or repression. Dashed brown links ending with bi- or uni-directional arrow(s) indicate binding and unbinding between proteins or protein transformation. Solid and dashed green links ending with a dot indicate degradation via ubiquitination by Skp2/APCFzy/APCFzr. ‘&’ means combined condition. The right panel shows abbreviations, full names and initial values (Supplementary Table 4) of 25 proteins and complexes described by 25 ordinary differential equations. (B) Signaling events are defined upon nonlinear molecular interactions. Shown is expression of gene g repressed by two inhibitors I1 and I2 and activated by two activators A1 and A2 independently at two enhancers. Repressive and activating Hill functions (Hr and Ha in the equation of dg/dt), with half-maximal activating/inhibiting coefficients, describe how I1, I2, A1 and A2 nonlinearly regulate g (functional concentration ranges of these regulators are indicated by shadowed areas). When I1, I2, A1, or A2 exceeds their half-maximal activating/inhibiting coefficients, event I1_Rep_g, I2_Rep_g, A1_Act_g, or A2_Act_g occurs. When I1_Rep_g and I2_Rep_g are absent and A1_Act_g is present at an enhancer, or A2_Act_g is present at the other enhancer, g_Exp_G occurs.
To uncover the control mechanisms of the accurate timing and order of cell cycle phases, considerable mathematical models have been built. In early 1990 s, pioneer theoretical studies examined the negative and positive feedbacks in the M phase2,3,4. In late 1990 s, a concise model was developed to simulate the four phases5. Since then, further studies have focused on either molecular details such as protein translocation between cytoplasm and nucleus6 and multisite phosphorylation7, or mechanistic properties such as robustness of cell cycles8 and mode lock behavior9. While it is well accepted that the control mechanisms in cells share common features10, these studies led to different hypotheses, especially the clock and domino hypotheses11, to explain strictly ordered G1/S/G2/M phases and there are points arguing for and against the importance of regulated proteolysis of cyclins and CDKs12,13,14. Moreover, while it is known the four phases are strictly ordered, it remains unclear to what extent signaling events should be ordered. The novel findings revealed by a recent experimental study15 suggest that the timing of some events denies the previous understanding (they occur earlier than previously assumed). Thus, to develop new computational methods and models to explore signaling events is important and a good hypothesis obtained should explain how orders of signaling events ensure both strictly ordered cell cycle phases and cell’s adaptive responses to regulatory signals.
The cell cycle control mechanism contains multiple coupled positive and negative feedbacks, including the well annotated Rb-E2F and Wee-Stg-CDKB feedbacks that control G1/S and G2/M phases16. In Drosophila, mutations of cyclin D and its sole partner Cdk4 have little effect in any tissue16 and the cyclin E/Cdk2, cyclin A/Cdk1 and cyclin B/Cdk1 complexes comprise the most parsimonious system to drive the G1/S/G2/M transition (reviewed in17,18). In Drosophila ectopic expression of cycE and stg, the rate-limiting positive regulators for G1/S and G2/M progression, truncates G1 and G2, yet the total length of cell cycle is largely maintained19. This indicates a regulatory connection between G1/S and G2/M phases. Reis et al. examined two explanations for the observed connection, proposed a long-range feedback between G1/S and G2/M and suggested that the feedback “is an active mechanism that derives from inherent properties of the cell cycle control apparatus”20. But, no quantitative examination of the feedback has been made. Cell cycle activities are frequently tuned by developmental signals and especially, cell divisions need to be stopped at precise times in developing tissues. In the developing Drosophila eye, a burst of stg expression in a band of cells (the morphogenetic furrow) makes most cells arrest in G121, but a few cells escape the G1 arrest to enter into a new round of division after cells past this round of mitosis22. It remains not accurately known how sustained cell cycles are stopped and how G1 arrest is escaped. Since the proposed long-range feedback between G1/S and G2/M enables the cell to adaptively shorten or elongate G1/S and G2/M phases, it should be physiologically important. Also, as seen in Drosophila wing, when cell cycles are perturbed by ectopic expression of dap, wee and myc, this mechanism enables cells to maintain the normal rate of division20. In contrast, cancerous cells often do not make compensatory changes23.
Most mathematical models of cell cycle control focused on the robust progression of either the G1/S or G2/M phases and examined robustness only upon oscillating protein concentrations7,24,25. Flexible orders of signaling events, which should be an important aspect of robustness, have never been explored. Based on abundant experimental findings about how dividing cells respond to developmental signals, we have developed a cell cycle model containing the most essential three Cdk modules to simulate G1/S/G2/M phases. The model was built upon key molecular interactions observed in mammalian cells and in Drosophila cells. The reasons for building such a model that integrates observations in mammals and Drosophila are that available observations in neither species are sufficient to formulate full and detailed feedbacks, the cell cycle control machinery is highly conserved in metazoans and Drosophila development shows rich phenotypes.
For the first time, the model produces not only oscillating protein concentrations but also periodic signaling events. Moreover, compared with previous models (including the recent ones26,27,28), it includes two Cdk inhibitors (Dap and Rux) that target different Cdk complexes and antagonistic E2Fs (E2F1 and E2F2) that function as positive and negative regulators. Simulations focus on the distinct roles of Dap, Rux, E2F1, E2F2, Stg and Wee in cell cycle control and generate results indicating that the E2F1-centered long-range feedback can regulate G1/S and G2/M phase compensation. More notably, simulations reveal that not all signaling events are essential and equally robust and that events of APC- and Skp2-conducted proteolysis of Cdk complexes should occur in a strict order. We postulate that while irreversibility of cell cycle phase progression is the consequence of systems-level feedbacks29, as originally proposed30 and recently examined28 the highly ordered proteolytic destruction of Cdk complexes is likely to be the most essential events. Our results indicate that flexible lengths of cell cycle phases and flexible orders of signaling events are intrinsically associated and are key features of robust cell cycle control.
Results
Parameterize the model upon signaling events
To investigate cell cycle control at the systems level, the interactions between 25 most essential proteins and their complexes are integrated into 25 differential equations based on experimental findings (reviewed in17,18,31) (Fig. 1; Supplementary Methods). Specifically, the interactions between E2F1 and CDKE/CDKA/CDKB are based on the findings that E2F1 regulates and is regulated by, multiple Cdk complexes and that these regulations may form a feedback between G1/S and G2/M progression20. Handle of the negative E2F protein E2F2 (E2F4 in mammals), which has been ignored in all previous models, is based on that E2F4 needs p27/p130 (but not Rb) to co-locate to E2F-responsive promoters of target genes, which include B-myb, CycA, Cdk1 and E2F132,33.
Molecular interactions are defined in the model and captured in simulations, including A_Act_B (A activates B), A_Ubi_B (A ubiquitinates B) and A_Rep_B (A represses B) (Figs 1 and 2). Upon experimental observations the model was parameterized to first produce oscillating protein concentrations and second to produce periodic signaling events (Fig. 2A; Supplementary Table 1). For most parameters, a large range allows them to generate oscillating protein concentrations, indicating robustness of the model (Supplementary Table 2). The ranges of some E2F2-, Skp2-, E2F1- and CDKE-related parameters are narrow. To make the model also generate periodic signaling events makes parameters biologically more qualified. Notice that while many parameter settings enable the model to produce oscillating protein concentrations, much fewer enable it to produce all periodic signaling events. Since the start of G1, S, G2 and M phases is featured by the maximal value of APCFzy, the rise of CycA, the rise of CDKBa and the maximal value of CDKBa, we let the start of G1/S/G2/M be marked by the stop of CDKBa_Ubi_E2F1, the stop of DapE2F2_Rep_CycA and the start of E2F1_Act_CycA, the start of Stga_Rep_CDKBi and the start of APCFzy_Ubi_CDKBi and APCFzy_Ubi_CDKBa, respectively (Fig. 1).
Computed protein concentrations and reconstructed signaling events.
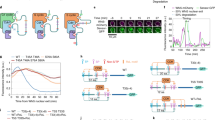
dX and sX are protein X’s synthesis and decay rates and aXY is the parameter in a Hill function describing how X activating Y nonlinearly. Each panel’s top and bottom parts show protein concentrations (between 0.0–1.0) and signaling events (indicated by elevated line segments). (A) Under the default parameters all signaling events occur periodically. (B) If the decay rate of active Stg is reduced (dStga = 1.0→0.3) cell cycle is arrested at G1 (not shown); but, if the reduction is accompanied by the removal of Dap from the system by setting the synthesis rate of Dap 0.0 (dStga = 1.0→0.3 & sDap = 1.0→0.0) escape of G1 arrest occurs. (C) If degradation of E2F1 mediated by CDKA occurs earlier (aCDKAE2F1 = 0.14→0.07) cell cycle does not occur, but if this change is accompanied by the removal of Rux (aCDKAE2F1 = 0.14→0.07 & sRux = 1.0→0.0) cell cycles are recovered (see the sharp down of Rux in simulation, proteins different from those in (A) and (B) are marked). (BC) were captured continuously as the parameters changed in simulation (see the sharp down of Dap). In (AB) the wild fluctuations of the first few cycles are caused by the initial conditions and changed parameter, not by noises.
The model can produce cell cycles with varied concentrations of the growth factor GF (a parameter in CycE’s equation) (Fig. 2A) and with the absence of Dap, Rux, or E2F2, respectively (Supplementary Figure 1). Low levels of GF, over a sufficient period, can turn E2F1 on and activate a cell cycle, whereas high levels of GF needs less time to reach the result. If GF is removed before and after a key time point in G1, cells either return back to a stable state or complete a cycle. The feedback between Rb and E2F1 forms a bistable switch enabling graded GF inputs to be converted into all-or-none E2F1 responses. The Cdk1-Wee-Stg system, with positive and double-negative feedbacks, is also bistable. These results are consistent with previous findings26,34,35,36,37. To include two Cdk inhibitors and antagonistic E2F proteins, which was not seen in previous models, is important for more realistically examining cell cycle control.
The E2F1-centered feedback between CDKE and CDKB influences the timing, duration and order of signaling events
After the above examinations, we then examined cell cycle phase compensation, an important indication of robustness and adaptiveness of cell cycle control. Reis and Edgar observed that when the G1 Cdk inhibitor Dap is overexpressed, G1/S are elongated, G2/M are shortened and the total cell cycle length is maintained and hypothesized that E2F1, which is down regulated by CDKE and CDKB, is the key regulator of cell cycle phase compensation20. To examine this hypothesis, we simulated dap overexpression. When sDap = 1.0→1.05 (“High Dap” in Fig. 3) (sX and dX indicate X’s synthesis and decay rate, respectively), Dap turns more CDKE into the inactive CDKEDap and fewer CDKE causes a delayed G1 and phosphorylates fewer E2F1 for ubiquitination. Accumulated E2F1 subsequently functions for a longer time to activate Stgi into Stga. Since more Stga quickly activates more CDKBa, the G2/M phases become shortened and CDKBa phosphorylates E2F1 for ubiquitination for a longer period. In the next round, E2F1 needs a longer time to accumulate to the threshold level to activate CycE (Fig. 3).
Changed timing, duration and order of signaling events caused by the E2F1-centered long-range negative feedback.
The stop of CDKBa_Ubi_E2F1 marks the start of G1. “High Dap” and “High Wee” indicate sDap = 1.0→1.05 and sWee = 1.0→1.8. Numbered arrows indicate events of interest. 1: E2F1 functions for a longer time to activate Stgi into Stga. 2: Fewer CDKE causes a delayed G1. 3: E2F1 needs a longer time to trigger E2F1_Act_CycE in next round. 4: Fewer CDKBa phosphorylates E2F1 for ubiquitination for a shorter period. 5: More accumulated E2F1 quickly triggers E2F1_Act_CycE.
Reis and Edgar also found that when the Cdk1 inhibitory kinase Wee is overexpressed the G2/M phases are elongated, following shortened G1/S phases20. Our model shows that, when sWee = 1.0→1.8 (“High Wee” in Fig. 3), increased Wee deters the transition of CDKBi to CDKBa and causes the elongated G2/M phases. Fewer CDKBa thus phosphorylates E2F1 for ubiquitination for a shorter period. When cells enter into the next G1 phase, the more accumulated E2F1 quickly activates CycE, resulting in a shortened G1/S (Fig. 3). These simulations indicate that when CDKE or CDKB becomes high to facilitate G1/S or G2/M transition, the negative regulation of E2F1 by CDKE and CDKB makes the down-regulated E2F1 deter the subsequent G2/M or G1/S transition (Table 1). If the mediated degradation of E2F1 by CDKE and CDKB is absent as in all previous models7,26, cell cycle phase compensation does not occur.
Cell cycle phase compensation influences not only the timing and duration of molecular interactions, but also their orders. Simulations demonstrate that the order of events indicating the onset of G1/S/G2/M remains the same, but the order of other events is changed. For example, events in the Rb-E2F1 feedback and the Cdk1-Wee-Stg feedbacks shift their relative order when dap and wee are overexpressed (Fig. 4). Thus, not all signaling events are strictly ordered. Inessential events can have flexible orders and essential or robust events have strict orders. This is comparable to the classification of parameters into “essential” ones and “modulatory” ones, which make a cell cycle model behaves differently to perturbations38.
The order of signaling events in a full cell cycle under different conditions.
Numbers without and with underlines indicate the start and stop of events (see Fig. 1), respectively. Red numbers indicate G1/S/G2/M events. Compared with the events in the Cdk1-Wee-Stg feedbacks (including 24, 25, 29, 30, 32 and 33) and events in the Rb-E2F1 feedback (including 5, 7, 14 and 15), events of protein ubiquitination (in green, from the column 42/44/45/46 to the column 9/10), have a robust order in the three situations. (A) Under default parameters. (B) dap overexpression (sDap = 1.0→1.05) and (C) wee overexpression (sWee = 1.0→1.8).
Negative regulators play distinct roles in cell cycle arrest and escape of arrest
We next examined cell cycle arrest and escape of cell cycle arrest, which occur widely in tissue and organ development. To explain the findings that cell divisions in the Drosophila eye are arrested in G1 in cells expressing stg and that Rux is essential for the cell cycle arrest21,39, Thomas et al. proposed a two-step process. First, cells in G1 are inhibited by some factor from entering into the S phase; second, cells in G2 are driven by Stg to go through M phase and after reentering into G1 they are prevented from reinitiating a new cell cycle21. This explanation suggests that for G1 arrest the repression of CycE and E2F1 is required. The S-phase Cdk inhibitor Rux was later found to physically associate with CDKA to facilitate G1 arrest40, but this does not adequately explain how E2F1 is repressed and why the expression of stg, a G2/M activator, causes cell cycle arrest.
To quantitatively explore Stg-induced cell cycle arrest, we simulated the impact of high level active Stg (dStga = 1.0→0.3). The increased Stg causes quicker accumulation and higher level of CDKBa, which directly produces three effects: shortened G2/M phases, decreased E2F1 level (due to CDKBa-mediated E2F1 degradation) and increased APCFzy level (due to CDKBa-activated Plx). Subsequently, because of the significantly decreased E2F1, activation of CycE and CycA does not occur and because of the increased APCFzy, CycA is further decreased. The CDKE-E2F1-CDKB feedback thus enables the high level of Stg, via degradation of E2F1 by CDKB, to make cell cycles arrested (Supplementary Figure 2).
To examine the role of Dap in the arrest of cell proliferation41,42, we simulated the impact of Dap with sDap = 1.0→0.0 together with dStga = 1.0→0.3. We found that in this situation cells re-entered into G1 and in a rapid pace (Fig. 2B), that is, the absence of the CDKE inhibitor Dap enables cells to escape from G1 arrest. Meanwhile, the absence of the CDKA inhibitor Rux and the absence of the negative E2F protein E2F2 do not have the role. In comparison, high levels of Dap and E2F2 alone can cause cell cycle arrest, but high levels of Rux are more tolerable (Table 2, Supplementary Figure 3–5).
Increased Stg needs Rux to arrest cells in G1, otherwise cells in rux mutant will bypass G1 and be arrested in S phase21,40. In simulations the removal of Rux does not enable the escape of G1 arrest under the condition dStga = 1.0→0.3 (Table 2), but can drive cell cycle progression under some conditions. For example, if aCDKAE2F1 = 0.14→0.07 cell cycle fails to occur; but if Rux is removed (aCDKAE2F1 = 0.14→0.07 + sRux = 1.0→0.0) cell cycles are recovered (Fig. 2C). In this case, as no CDKA is bound by Rux, swinging CycA gradually produces enough oscillating CDKA for entering into the S phase (Fig. 2C). These results reveal distinct roles of Dap, Rux and E2F2. These three negative regulators are dispensable under the default parameters and probably under many physiological conditions, but enable the core control system to respond flexibly to regulatory signals. Together, Fig. 2B,C suggest that functions of Dap and Rux are distinct and context-dependent. While they may be dispensable as extra regulators of CDKE and CDKA, Dap influences cell cycles more significantly because it inactivates CDKE and activates E2F2, while Rux only inactivates CDKA. These suggest that Dap and Rux should be handled differently in computational studies.
Robustness of cell cycles allows flexible orders of signaling events
Upon the consensus that biological signaling should be robust against errors and noises, many previous studies carefully checked if a model is sensitive to changes of initial conditions and parameter values8,43. However, ups and downs of a protein’s concentration can be caused by multiple regulators in complex ways and not all parameter changes alter the occurrence and/or the order of signaling events. A more essential question may be to what extent cell cycle control can tolerate changes of signaling events.
Simulations of cell cycle phase compensation indicate that the increase of Dap and Wee changes some signaling events (Figs 3 and 4). As the equation of APCFzy shows, the timing of Plx_Act_APCFzy is determined by the parameter aPlxFzy:

The smaller the parameter aPlxFzy is, the earlier the event Plx_Act_APCFzy occurs. To examine to what extent the model is robust against changes of signaling events, we conducted simulations with parameters in Hill functions increased and decreased by 66.6%. In most cases cell cycles occurred (Table 3), indicating that the model is highly robust in the conventional sense. To ensure such results are not specific to this set of parameters, we identified two more sets of parameters that enable the model to generate all signaling events and repeated the simulations with parameters in Hill functions increased and decreased by 66.6% (Supplementary Table 3).
Upon results in Table 3 and Supplementary Table 3, events can be classified into three groups with respect to the alterations in their occurrence with perturbations to the system. The first are critical events that occur periodically with accurate timing. Many Skp2, E2F2 and CDKE events belong to this group, as the changes of parameters cause cell cycle fail. The opposite are robust events that occur robustly with considerably changed timing (most APCFzy and APCFzr events). Other events are in between, some cannot occur too early but can be late or absent, some cannot occur too late but can be present early, while all protein concentrations oscillate. Multiple statistical treatments of all events captured in three batches of simulations (Table 3, Supplementary Table 3, Supplementary Table 5) indicate that proteolysis events conducted by APCFzy and APCFzr and events conducted by CDKBa are significantly more robust than other events - their occurrence is hardly influenced by the increase and decrease of the controlling parameter. Such events, we posit, should be important. Bifurcation analysis also reveals that the model is sensitive to changes of E2F1 and E2F2 parameters (Supplementary Figure 7, 8).
To further examine the negative regulator Dap and Rux, we repeated all simulations described in Table 3 with the removal of Dap or Rux (sDap = 0.0 or sRux = 0.0) respectively. Compared with 14 failed cases (cell cycle fails) under all the parameter settings in Table 3, there were 10 failed cases when additionally sDap = 0.0 and 17 failed cases when additionally sRux = 0.0. This indicates that cell cycle progression is facilitated when the CDKE inhibitor Dap is absent, but is not when the CDKA inhibitor Rux is absent. Indeed, Rux mediates cells to enter into the S phase instead of entering into a new G1. The robustness of cell cycles against changes of signaling events and the classification of different events, for the first time, reveal a new dimension of cell cycle control. Similar to the conclusion from budding yeast28, these results suggest that, to a considerable extent, irreversibility of cell cycle phases is ensured by the robustness of timely destruction of cyclins and cyclin/Cdk complexes.
In simulations, when the parameter in some Hill functions is changed, it changes other events instead of, or together with, the defined one. For example, when aFzrCycB is increased by even 50%, event 24, 25, 26 and 27 become absent, because delayed destruction of CycB allows more CDKBi and CDKBa to be formed. Simulations reveal that since the total amount of Cdk1 is a constant in the model, the binding of more CycB to Cdk1 hinders the binding of CycA to Cdk1. If the total amount of Cdk1 or the binding affinity of CycA/Cdk1 is increased, the absence of event 24, 25, 26 and 27 does not occur. Whether the delayed destruction of CycB by APCFzr influences CycA/Cdk1 binding is unreported and an interesting issue for experimental investigation.
Discussion
Robustness as an essential property of cell cycle control has been examined by numerous studies, but its nature remains elusive. As experimental studies have uncovered considerable molecular interactions, intensive computational studies become not only necessary but also feasible. There are two challenges for one to build a computational model. The first is to select molecular interactions observed probably in more than one species; the second is to identify proper parameters to formalize molecular interactions. For the first, a model based on findings in one species has both pros and cons – data consistency is ensured, but assumptions are made due to data insufficiency. We think if conclusions do not ostensibly rely on detailed molecular interactions and molecular interactions are highly conserved, fewer assumptions on missing links in data and more findings from multiple species should be more preferable. In this study, the main conclusion - signaling events show flexible orders and key events show a robust order - should not sensitively rely on particular molecular interactions.
Multiple methods have been used in previous practices, including (1) to use numerical screening and specific sampling methods to explore the parameter space, (2) to explore constraints between parameters, (3) to tune a model to produce the wild-type phenotype and (4) to prove that conclusions are independent of specific parameters. In this study we identify parameters not only upon the combined use of the above methods (except (1)), but also, for the first time, upon the generation of periodic signaling events. We find that many parameters enable the model to produce oscillating protein concentrations, but much fewer enable it to produce all signaling events. Based on the novel methods and results, the model reveals that robustness of cell cycle control determines the strict order of key events and allows flexible orders of other signaling events. Robust cell cycle control against changes of signaling events opens a new dimension of robust biological signaling. We do not claim that our analysis of signaling events is flawless, only that it may promote understanding the orders of signaling, in cell cycle control in particular and in multiple pathway interplay in general.
A question is, to what extent do the simulated events occur in cells? We point out that events are determined by protein concentrations that are computed using the widely adopted methods in previous studies, making periodic signaling events as convincing as oscillating protein concentrations. Further, in simulations if a protein’s concentration does not reach the defined threshold the defined event does not occur. Although this does not necessarily mean that the event would be absent in vivo, based on the well accepted mass-action rule, this stipulates that at least the event would occur for a shorter period in vivo, causing the order of related events likely changed. Thus, orders of events under in vivo situations can be reasonably examined by simulations.
The cell cycle control system comprises multiple and redundant components and feedbacks, among them are multiple Cdk inhibitors (e.g., Dap and Rux), regulators of feedbacks (e.g., Stg and Wee) and antagonistic E2F proteins (e.g., E2F1 and E2F4). In addition to the balance between Rb and E2F1, a balance between positive and negative E2Fs is also important44,45,46 and so far the roles of negative E2Fs and different Cdk inhibitors remain poorly understood. An important, but largely ignored, aspect of robust cell cycle control is the flexible phase compensation. Flexible lengths of cell cycle phases have been observed and examined in yeast27,47,48, but they are more important for and less understood in tissue and organ development in metazoans. As seen in Drosophila development, following prolonged G1/S or G2/M a cell produces shortened G2/M or G1/S to robustly maintain the total length of cell cycles20,49. Our model demonstrates how the CDKE-E2F1-CDKB long-range feedback, with the participation of inhibiting regulators such as Dap, Rux and E2F2, realizes cell phase compensation and cell cycle arrest. For example, if E2F2 is absent, when Dap is low, the increased CDKE would mediate strong E2F1 degradation and cause escape from G1 arrest not to occur.
In cell cycles G1/S/G2/M phases are strictly ordered, but details remain controversial or unclear, including how the S phase and M phase are ordered50, how temporal ordering of mitotic exit events is achieved14,51 and to what extent signaling events should be ordered. Multiple mechanisms are proposed to explain ordered cell cycle progression11,52, including that the order of late mitotic events depends on the order in which different Cdk and APC substrates are dephosphorylated and destroyed31,51. The irreversibility of cell cycle progression is also argued not a consequence of protein degradation, instead, progression through the cell cycle is more like the cycle of a clothes washing machine and events must occur in a specific order53. Given that regulatory crosstalk between G1/S/G2/M phases widely exists19,54,55,56, it is important to explore to what extent signaling events are ordered. Our model demonstrates that many events can have flexible orders, or even be absent or persistently present. Since multiple feedbacks work in parallel and redundantly in cells, the flexible occurrence and orders of events are not a surprise and successive events that maintain their relative orders under all conditions can be seen as “motifs” that indicate modularity of signaling.
Our simulations also reveal which events are more robust or critical than others. For example, to initiate a round of cell cycle CDKE activates E2F1, represses E2F2 and represses APCFzr. Thus, CDKE-related events are rather critical and sensitive to parameter changes. On the other hand, simulations under varied parameter settings reveal that the events of proteolysis of cyclins and Cdk complexes occur more robustly and are more strictly ordered than other events (Table 3, Supplementary Table 3, Supplementary Table 5). These results, together with the flexible coupling between the long-range CDKE-E2F1-CDKB feedback and the short-range Rb-E2F1 and Cdk1-Wee-Stg feedbacks under varied conditions, indicate that events in cells follow neither the domino nor the clock models11 because both of which stipulate a strict order, but agree better with the clothes washing machine hypothesis. We suggest that the flexibility and robustness of the cell cycle control can be more accurately metaphorized by a gear system - big and small gears, at different times and upon different regulatory signals, can be coupled in multiple ways to produce different events with flexible orders and to speed up or slow down specific cell cycle phases. The identification of more and more components participating in cell cycle regulation in a context-dependent manner strongly justifies this gear system model.
Methods
Formulate the model
The model uses 25 non-dimensionalized differential equations to describe interactions between 25 proteins and their complexes (Fig. 1; Supplementary Methods). Some technical details are as follows. First, unlike previous models6,7,25, upon the recent experimental findings36,57 we do not handle proteins’ multiple phosphorylation sites. Instead, proteins simply have active and inactive states (which correspond to all sites being either phosphorylated or dephosphorylated) and the transition between the two states is switch-like and controlled by the competition between the protein and its modifiers. Given that the Hill coefficient for Stg activation by Cdk1 is about 1158, coefficient = 6 is set in all Hill functions (except in the Rb auto-dephosphorylation process). Second, different methods have been used to describe nonlinearity of protein-protein interactions; we adopt the method that allows the modification of a protein to depend nonlinearly on the concentrations of its modifiers and linearly on the concentration of itself11. Third, since Cdks do not visibly fluctuate and overexpression of cycE can increase Cdk2 activity20, Cdks are at the maximal level but cyclins are at low levels. Fourth, we assume that different phosphorylation states do not affect a protein’s half-life.
Parameterize the model
There are eight groups of parameters, including (1) s (synthesis rates), (2) d (decay rates), (3) u (SCF- or APC-mediated ubiquitination), (4) p (kinase- or phosphorylase-mediated phosphorylation or dephosphorylation), (5) k (binding), (6) kk (unbinding), (7) a (half maximal activation coefficient in Hill functions) and (8) r (half maximal repression coefficient in Hill functions) (Supplementary Methods). We first evaluated the ranges of parameters upon literature review, then explored the constraints between parameters and finally determined the values of parameters by tuning the model to produce oscillating protein concentrations and periodic signaling event. We deliberately adopted a set of very simple initial conditions (Supplementary Table 4). Unrealistic though, they clearly indicate that the model does not demand specific initial conditions. Results in the main text are based on the set of parameters and the set of initial conditions.
To make analysis of events more reliable, we performed simulations with two more sets of parameters and to facilitate bifurcation analysis we identified a second set of initial conditions. XPPAUT is used to examine the ranges of parameters.
Solve the equations
Equations are solved under Linux using the second-order forward Runge-Kutta method with adaptive time steps controlled by two error thresholds. For a protein U described by  , the error control should meet
, the error control should meet  . Here err =
. Here err =  ,
,  ,
,  and relerr = abserr = 0.00001. In simulations, as long as
and relerr = abserr = 0.00001. In simulations, as long as  the time step is halved. The C code is available upon request.
the time step is halved. The C code is available upon request.
Capture signaling events
Using a programming tool we developed59, we define that, when the concentration of protein A reaches the half-maximal activation/repression coefficient in the Hill function describing how A nonlinearly activates/represses protein B, A sends the message activation or repression to B (the events are abbreviated as A_Act_B or A_Rep_B) (Fig. 1B). For example, when Skp2 > aSkp2CycE, Skp2 sends the message ubiquitination to CycE and the message received in CycE is captured as the event Skp2_Ubi_CycE. In simulations all events are continuously captured in cells and the windows showing signaling events and protein concentrations are captured using the program GIMP.
Bifurcation analysis
With the original set of parameters and the new set of initial conditions, we used the program oscill8 to perform bifurcation analysis.
Statistical analysis
Upon Table 3 and Supplementary Table 3, we quantify the model’s responses to changed timing of events by ranking 0/0 = 1, 0/1 = 2, 0/2 = 3, 1/1 = 4, 1/2 = 5, 2/2 = 6 (0, 1 and 2 indicate that protein concentrations do not oscillate, protein concentrations oscillate but some events do not occur periodically and all events occur periodically). We then performed the global F test for all of the events, after which multiple comparisons (including Tamhane’s T2 multiple comparison test) were made.
Additional Information
How to cite this article: Zhu, H. and Mao, Y. Robustness of cell cycle control and flexible orders of signaling events. Sci. Rep. 5, 14627; doi: 10.1038/srep14627 (2015).
References
Hartwell, L. H. & Weinert, T. Checkpoints: controls that ensure the order of cell cycle events. Science 246, 629–634 (1989).
Goldbeter, A. A minimal cascade model for the mitotic oscillator involving cyclin and cdc2 kinase. Proc Nati Acad Sci USA 88, 9107–9111 (1991).
Novak, B. & Tyson, J. J. Numerical analysis of a comprehensive model of M-phase control in Xenopus oocyte extracts and intact embryos. J Cell Sci 106, 1153–1168 (1993).
Tyson, J. J. Modeling the cell division cycle: cdc2 and cyclin interactions. Proc Natl Acad Sci USA 88, 7328–7332 (1991).
Novak, B., Csikasz-Nagya, A., Gyorffya, B., Chen, K. & Tyson, J. J. Mathematical model of the fission yeast cell cycle with checkpoint controls at the G1/S, G2/M and metaphase/anaphase transitions. Biophys Chem 72, 185–200 (1998).
Yang, L., Han, Z., Robb MacLellan, W., Weiss, J. N. & Qu, Z. Linking cell division to cell growth in a spatiotemporal model of the cell cycle. J Theor Biol 241, 120–133, 10.1016/j.jtbi.2005.11.020 (2006).
Barik, D., Baumann, W. T., Paul, M. R., Novak, B. & Tyson, J. J. A model of yeast cell-cycle regulation based on multisite phosphorylation. Mol Syst Biol 6, 405, 10.1038/msb.2010.55 (2010).
Li, F., Long, T., Lu, Y., Ouyang, Q. & Tang, C. The yeast cell-cycle network is robustly designed. Proc Natl Acad Sci USA 101, 4781–4786, 10.1073/pnas.0305937101 (2004).
Cross, F. & Siggia, E. Mode locking the cell cycle. Phys Rev E Stat Nonlin Soft Matter Phy 72, 10.1103/PhysRevE.72.021910 (2005).
Csikasz-Nagy, A., Battogtokh, D., Chen, K. C., Novak, B. & Tyson, J. J. Analysis of a generic model of eukaryotic cell-cycle regulation. Biophys J 90, 4361–4379, 10.1529/biophysj.106.081240 (2006).
Ferrell, J. E. Jr., Tsai, T. Y. & Yang, Q. Modeling the cell cycle: why do certain circuits oscillate? Cell 144, 874–885, 10.1016/j.cell.2011.03.006 (2011).
Novak, B., Tyson, J. J., Gyorffy, B. & Csikasz-Nagy, A. Irreversible cell-cycle transitions are due to systemslevel feedback. Nat Cell Biol 9, 724–728 (2007).
Potapova, T. A. et al. The reversibility of mitotic exit in vertebrate cells. Nature 440, 954–958, 10.1038/nature04652 (2006).
Wittenberg, C. Cell cycle: A division duet. Nature 481, 273–274, 10.1038/nature10828 (2012).
Akopyan, K. et al. Assessing kinetics from fixed cells reveals activation of the mitotic entry network at the S/G2 transition. Mol Cell 53, 843–853, 10.1016/j.molcel.2014.01.031 (2014).
Morgan, D. O. The cell cycle: Principle of control. Oxford University Press (2007).
Edgar, B. A. & Lehner, C. F. Developmental control of cell cycle regulators: A fly's perspective. Science 274, 1646–1652 (1996).
Lee, L. A. & Orr-Weaver, T. L. Regulation of cell cycles in Drosophila development: intrinsic and extrinsic cues. Annu Rev Genet 37, 545–578, 10.1146/annurev.genet.37.110801.143149 (2003).
Neufeld, T. P., de la Cruz, A. F., Johnston, L. A. & Edgar, B. A. Coordination of growth and cell division in the Drosophila wing. Cell 93, 1183–1193 (1998).
Reis, T. & Edgar, B. A. Negative regulation of dE2F1 by cyclin-dependent kinases controls cell cycle timing. Cell 117, 253–264 (2004).
Thomas, B. J., Gunning, D. A., Cho, J. & Zipursky, L. Cell cycle progression in the developing Drosophila eye: roughex encodes a novel protein required for the establishment of G1. Cell 77, 1003–1014 (1994).
Baker, N. E. Cell proliferation, survival and death in the Drosophila eye. Semin Cell Dev Biol 12, 499–507, 10.1006/scdb.2001.0274 (2001).
Sherr, C. J. The Pezcoller lecture: cancer cell cycles revisited. Cancer Res 60, 3689–3695 (2000).
Pomerening, J. R., Kim, S. Y. & Ferrell, J. E. Jr. Systems-level dissection of the cell-cycle oscillator: bypassing positive feedback produces damped oscillations. Cell 122, 565–578, 10.1016/j.cell.2005.06.016 (2005).
Haberichter, T. et al. A systems biology dynamical model of mammalian G1 cell cycle progression. Mol Syst Biol 3, 84, 10.1038/msb4100126 (2007).
Gerard, C. & Goldbeter, A. Temporal self-organization of the cyclin/Cdk network driving the mammalian cell cycle. Proc Natl Acad Sci USA 106, 21643–21648, 10.1073/pnas.0903827106 (2009).
Oguz, C. et al. A stochastic model correctly predicts changes in budding yeast cell cycle dynamics upon periodic expression of CLN2. PLoS One 9, e96726, 10.1371/journal.pone.0096726 (2014).
Freire, P., Vinod, P. K. & Novak, B. Interplay of transcriptional and proteolytic regulation in driving robust cell cycle progression. Mol Biosyst 8, 863–870, 10.1039/c2mb05406j (2012).
Lopez-Aviles, S., Kapuy, O., Novak, B. & Uhlmann, F. Irreversibility of mitotic exit is the consequence of systems-level feedback. Nature 459, 592–595, 10.1038/nature07984 (2009).
King, R. W., Deshaies, R. J., Peters, J.-M. & Kirschner, M. W. How proteolysis drives the cell cycle. Science 274, 1652–1659 (1996).
Sullivan, M. & Morgan, D. O. Finishing mitosis, one step at a time. Nat Rev Mol Cell Biol 8, 894–903, 10.1038/nrm2276 (2007).
Rayman, J. B. et al. E2F mediates cell cycle-dependent transcriptional repression in vivo by recruitment of an HDAC1/mSin3B corepressor complex. Genes Dev 16, 933–947, 10.1101/gad.969202 (2002).
Pippa, R. et al. p27Kip1 represses transcription by direct interaction with p130/E2F4 at the promoters of target genes. Oncogene 31, 4207–4220, 10.1038/onc.2011.582 (2012).
Pomerening, J. R., Sontag, E. D. & Ferrell, J. E. Jr. Building a cell cycle oscillator: hysteresis and bistability in the activation of Cdc2. Nat Cell Biol 5, 346–351, 10.1038/ncb954 (2003).
Sha, W. et al. Hysteresis drives cell-cycle transitions in Xenopus laevis egg extracts. Proc Natl Acad Sci USA 100, 975–980, 10.1073/pnas.0235349100 (2003).
Kim, S. Y. & Ferrell, J. E. Jr. Substrate competition as a source of ultrasensitivity in the inactivation of Wee1. Cell 128, 1133–1145, 10.1016/j.cell.2007.01.039 (2007).
Yao, G., Lee, T. J., Mori, S., Nevins, J. R. & You, L. A bistable Rb-E2F switch underlies the restriction point. Nat Cell Biol 10, 476–482, 10.1038/ncb1711 (2008).
Eriksson, O., Andersson, T., Zhou, Y. & Tegner, J. Decoding complex biological networks - tracing essential and modulatory parameters in complex and simplified models of the cell cycle. BMC Syst Biol 5, 123 (2011).
Thomas, B. J. et al. roughex down-regulates G2 cyclins in G1. Genes Dev 11, 1289–1298, 10.1101/gad.11.10.1289 (1997).
Avedosov, S. N., Krasnoselskaya, I., Mortin, M. & Thomas, B. J. Roughex mediates G1 arrest through a physical association with cyclin A. Mol Cell Biol 20, 8220–8229 (2000).
de Nooij, J. C., Letendre, M. A. & Hariharan, I. K. A cyclin-dependent kinase inhibitor, Dacapo, is necessary for timely exit from the cell cycle during Drosophila embryogenesis. Cell 87, 1237–1247 (1996).
Lane, N. E., Sauer, K., Wallace, K., Jan, Y. N. & Lehner, C. F. Dacapo, a cyclin-dependent kinase inhibitor, stops cell proliferation during Drosophila development. Cell 87, 1225–1235 (1996).
Tsai, T. Y. et al. Robust, tunable biological oscillations from interlinked positive and negative feedback loops. Science 321, 126–129, 10.1126/science.1156951 (2008).
Crosby, M. E., Jacobberger, J., Gupta, D., Macklis, R. M. & Almasan, A. E2F4 regulates a stable G2 arrest response to genotoxic stress in prostate carcinoma. Oncogene 26, 1897–1909, 10.1038/sj.onc.1209998 (2007).
Crosby, M. E. & Almasan, A. Opposing roles of E2Fs in cell proliferation and death. Cancer Biol Ther 3, 1208–1211 (2004).
Plesca, D., Crosby, M. E., Gupta, D. & Almasan, A. Maintaining G2-arrest to prevent mitotic entry with damaged DNA. Cell Cycle 6, 1147–1152 (2007).
Havens, C. & Walter, J. C. Mechanism of CRL4Cdt2, a PCNA-dependent E3 ubiquitin ligase. Genes Dev 25, 1568–1582 (2011).
Di Talia, S., Skotheim, J. M., Bean, J. M., Siggia, E. D. & Cross, F. R. The effects of molecular noise and size control on variability in the budding yeast cell cycle. Nature 448, 947–951 (2007).
Zhu, W., Giangrande, P. H. & Nevins, J. R. E2Fs link the control of G1/S and G2/M transcription. EMBO J 23, 4615–4626, 10.1038/ (2004).
Krasinska, L. et al. Protein phosphatase 2A controls the order and dynamics of cell-cycle transitions. Mol Cell 44, 437–450, 10.1016/j.molcel.2011.10.007 (2011).
Bouchoux, C. & Uhlmann, F. A quantitative model for ordered Cdk substrate dephosphorylation during mitotic exit. Cell 147, 803–814, 10.1016/j.cell.2011.09.047 (2011).
Morgan, D. O. The hidden rhythms of the dividing cell. Cell 141, 224–226, 10.1016/j.cell.2010.03.042 (2010).
Tyson, J. J. & Novak, B. Temporal organization of the cell cycle. Curr Biol 18, R759–R768, 10.1016/j.cub.2008.07.001 (2008).
Nurse, P. & Thuriaux, P. Regulatory genes controlling mitosis in the fission yeast Schizosaccharomyces pombe. Genetics 96, 627–637 (1980).
Russell, P. & Nurse, P. cdc25 functions as an inducer in the mitotic control of fission yeast. Cell 45, 145–153 (1986).
Resnitzky, D., Gossen, M., Bujard, H. & Reed, S. I. Acceleration of the G1/S phase transition by expression of cyclins D1 and E with an inducible system. Mol Cell Biol 14, 1669–1679 (1994).
Yang, Q. & Ferrell, J. E. Jr. The Cdk1-APC/C cell cycle oscillator circuit functions as a time-delayed, ultrasensitive switch. Nat Cell Biol 15, 519–525, 10.1038/ncb2737 (2013).
Trunnell, N. B., Poon, A. C., Kim, S. Y. & Ferrell, J. E. Jr. Ultrasensitivity in the regulation of Cdc25C by Cdk1. Mol Cell 41, 263–274, 10.1016/j.molcel.2011.01.012 (2011).
Zhu, H., Wu, Y., Huang, S., Sun, Y. & Dhar, P. Cellular automata with object-oriented features for parallel molecular network modeling. IEEE Trans Nanobioscience 2, 141–148 (2005).
Xu, M., Sheppard, K.-A., Peng, C.-Y., Yee, A. S. & Piwnica-Worms, H. Cyclin A/CDK2 binds directly to E2F-1 and inhibits the DNA-binding activity of E2F-1/DP-1 by phosphorylation. Mol Cell Biol 12, 8420–8431 (1994).
Kitagawa, M. H. et al. Phosphorylation of E2F-1 by cyclin A-cdk2. Oncogene 10, 229–236 (1995).
Shibutani, S. T. et al. Intrinsic negative cell cycle regulation provided by PIP box- and Cul4Cdt2-mediated destruction of E2f1 during S phase. Dev Cell 15, 890–900, 10.1016/j.devcel.2008.10.003 (2008).
Zielke, N. et al. Control of Drosophila endocycles by E2F and CRL4(CDT2). Nature 480, 123–127, 10.1038/nature10579 (2011).
Rossi, M. et al. Regulation of the CRL4(Cdt2) ubiquitin ligase and cell-cycle exit by the SCF (Fbxo11) ubiquitinligase. Mol Cell 49, 1159–1166 (2013).
Malumbres, M. & Barbacid, M. Mammalian cyclin-dependent kinases. Trends Biochem Sci 30, 630–641, 10.1016/j.tibs.2005.09.005 (2005).
Zielke, N., Querings, S., Rottig, C., Lehner, C. & Sprenger, F. The anaphase-promoting complex/cyclosome (APC/C) is required for rereplication control in endoreplication cycles. Genes Dev 22, 1690–1703, 10.1101/gad.469108 (2008).
Narbonne-Reveau, K. et al. APC/CFzr/Cdh1 promotes cell cycle progression during the Drosophila endocycle. Development 135, 1451–1461, 10.1242/dev.016295 (2008).
Moberg, K. H., Bell, D. W., Wahrer, D. C. R., Haber, D. A. & Hariharan, I. K. Archipelago regulates Cyclin E levels in Drosophila and ismutated in human cancer cell lines. Nature 413, 311–316 (2001).
Guardavaccaro, D. & Pagano, M. Stabilizers and destabilizers controlling cell cycle oscillators. Mol Cell 22, 1–4, 10.1016/j.molcel.2006.03.017 (2006).
Amati, B. & Vlach, J. Kip1 meets SKP2: new links in cell-cycle control. Nat Cell Biol 1, E91–E93 (1999).
Dui, W. et al. The Drosophila F-box protein dSkp2 regulates cell proliferation by targeting Dacapo for degradation. Mol Biol Cell 24, 1676–1687, S1–7, 10.1091/mbc.E12-10-0772 (2013).
Kolupaeva, V. & Janssens, V. PP1 and PP2A phosphatases—cooperating partners in modulating retinoblastoma protein activation. FEBS J 280, 627–643 (2013).
Lehman, D. A. et al. Cis-regulatory elements of the mitotic regulator, string/Cdc25. Development 126, 1793–1803 (1999).
Yao, G., Tan, C., West, M., Nevins, J. R. & You, L. Origin of bistability underlying mammalian cell cycle entry. Mol Syst Biol 7, 485, 10.1038/msb.2011.19 (2011).
Macaluso, M., Montanari, M. & Giordano, A. Rb family proteins as modulators of gene expression and new aspects regarding the interaction with chromatin remodeling enzymes. Oncogene 25, 5263–5267, 10.1038/sj.onc.1209680 (2006).
Foley, E., O'Farrell, P. H. & Sprenger, F. Rux is a cyclin-dependent kinase inhibitor (CKI) specific for mitotic cyclic-Cdk complexes. Curr Biol 9, 1392–1402 (1999).
Fung, T. K., Ma, H. T. & Poon, R. Y. Specialized roles of the two mitotic cyclins in somatic cells: cyclin A as an activator of M phase-promoting factor. Mol Biol Cell 18, 1861–1873, 10.1091/mbc.E06-12-1092 (2007).
Watanabe, N. et al. Cyclin-dependent kinase (CDK) phosphorylation destabilizes somatic Wee1 via multiple pathways. Proc Natl Acad Sci USA 102, 11663–11668, 10.1073/pnas.0500410102 (2005).
Kitagawa, M. et al. Phosphorylation of E2F-1 by cyclin A-cdk2. Oncogene 10, 229–236 (1995).
Wolthuis, R. et al. Cdc20 and Cks direct the spindle checkpoint-independent destruction of cyclin A. Mol Cell 30, 290–302, 10.1016/j.molcel.2008.02.027 (2008).
Felix, M. A., Labbe, J. C., Doree, M., Hunt, T. & Karsenti, E. Triggering of cyclin degradation in interphase extracts of amphibian eggs by cdc2 kinase. Nature 346, 379–382 (1990).
Wei, W. et al. Degradation of the SCF component Skp2 in cell-cycle phase G1 by the anaphase-promoting complex. Nature 428, 194–198 (2004).
Bashir, T., Dorrello, N. V., Amador, V., Guardavaccaro, D. & Pagano, M. Control of the SCFSkp2–Cks1 ubiquitin ligase by the APC/CCdh1 ubiquitin ligase. Nature 428, 190–193 (2004).
Acknowledgements
We gratefully acknowledge the Guangdong Province Foundation for Returned Scholars and the National Natural Science Foundation of China (31071165).
Author information
Authors and Affiliations
Contributions
H.Z. and Y.M. designed the study. H.Z. performed the study and wrote the manuscript. Y.M. revised the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhu, H., Mao, Y. Robustness of cell cycle control and flexible orders of signaling events. Sci Rep 5, 14627 (2015). https://doi.org/10.1038/srep14627
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep14627
This article is cited by
-
β-lapachone suppresses tumour progression by inhibiting epithelial-to-mesenchymal transition in NQO1-positive breast cancers
Scientific Reports (2017)
-
Quantitative Systems Biology to decipher design principles of a dynamic cell cycle network: the “Maximum Allowable mammalian Trade–Off–Weight” (MAmTOW)
npj Systems Biology and Applications (2017)
-
Robustness of cell cycle control and flexible orders of signaling events
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.