Abstract
Extracting community structure of complex network systems has many applications from engineering to biology and social sciences. There exist many algorithms to discover community structure of networks. However, it has been significantly under-explored for networks with positive and negative links as compared to unsigned ones. Trying to fill this gap, we measured the quality of partitions by introducing a Map Equation for signed networks. It is based on the assumption that negative relations weaken positive flow from a node towards a community and thus, external (internal) negative ties increase the probability of staying inside (escaping from) a community. We further extended the Constant Potts Model, providing a map spectrum for signed networks. Accordingly, a partition is selected through balancing between abridgment and expatiation of a signed network. Most importantly, multi-scale spectrum of signed networks revealed how informative are negative ties in different scales and quantified the topological placement of negative ties between dense positive ones. Moreover, an inconsistency was found in the signed Modularity: as the number of negative ties increases, the density of positive ties is neglected more. These results shed lights on the community structure of signed networks.
Similar content being viewed by others
Introduction
During the last decade, there has been an ever-growing interest in community structure of real-world networks1,2. A community structure is observed on a network when relations are sparse and there exists a mechanism driving density heterogeneity3,4. Indeed, grouping a network into modules of relatively high density provides novel insights into characteristics of a network5,6,7,8,9. However, the mainstream of this trend is mostly involved with only positive relations, where the links are absorptive and thus “more links” means “more closeness”. In parallel with this trend, there has been some attempts towards community detection in networks with both positive and negative relations1,10,11. As a result, the objective is to partition a network into modules of relatively high density with as few internal negative ties as possible. Hence, this is different from those that are not bound to the density constraint, e.g., Correlation Clustering12.
A community is a group of tightly knitted nodes that are weakly connected to the rest of the network. This is not a definition per se, nonetheless it is the one upon which literature is mostly agreed and can be further refined into specific definitions13. For signed graphs, the extension is straightforward by adding “as few internal negative ties as possible” criterion. Despite a vast literature on community detection, there has been few attempts towards signed networks1. Nonetheless, as the main step, Traag and Bruggeman generalized the modularity-alike objectives to signed graphs, as they have straightforward and intuitive signed counterparts14. However, the generalized form introduces a set of crucial parameters that cannot be trivially set. For the case of modularity, the objective function proposed by Gómez et al.15 is as:

where G+ (G−) is the positive (negative) subgraph of G, C is the partition and 0 ≤ α ≤ 1 is the relative importance of positive subgraph compared to the negative one, which has been set to  15. This objective function rewards (punishes) more positive (negative) density inside modules. In this work, we developed specialized algorithms for discovering community structure in signed networks. We first reformulated the Map Equation to measure the quality of partitions, known as Minimum Description Length (MDL). Next, we extended Constant Pots Model (CPM) to collect a spectrum of partitions from highly simplified to detailed ones, by sliding its parameter λ from zero to one (Fig. 1a,b). Based on these extensions, the community detection is carried out by minimizing MDL on λ-spectrum (Fig. 1c). Moreover, by comparing MDL and the ratio of internal negative (positive) links, the role and topological placement of negative ties can be quantified (Fig. 1d). As the experiments will show, the proposed method is highly reliable on both signed and unsigned networks, overcoming the resolution-limit and inconsistency of Modularity on signed networks. To evaluate the method, we proposed a novel benchmark in which negative ties can be informatively introduced. As a motivation, evaluating the effectiveness of signed detectors is possible only if the negative ties are informative and, to the best of our knowledge, this issue has not been addressed in previous works.
15. This objective function rewards (punishes) more positive (negative) density inside modules. In this work, we developed specialized algorithms for discovering community structure in signed networks. We first reformulated the Map Equation to measure the quality of partitions, known as Minimum Description Length (MDL). Next, we extended Constant Pots Model (CPM) to collect a spectrum of partitions from highly simplified to detailed ones, by sliding its parameter λ from zero to one (Fig. 1a,b). Based on these extensions, the community detection is carried out by minimizing MDL on λ-spectrum (Fig. 1c). Moreover, by comparing MDL and the ratio of internal negative (positive) links, the role and topological placement of negative ties can be quantified (Fig. 1d). As the experiments will show, the proposed method is highly reliable on both signed and unsigned networks, overcoming the resolution-limit and inconsistency of Modularity on signed networks. To evaluate the method, we proposed a novel benchmark in which negative ties can be informatively introduced. As a motivation, evaluating the effectiveness of signed detectors is possible only if the negative ties are informative and, to the best of our knowledge, this issue has not been addressed in previous works.
The proposed method.
A spectrum of partitions C(λ) and C+(λ) is created by applying the extended CPM on a signed graph (a) and its positive subgraph (b). The best community is the one with the lowest MDL (c). Also, by comparing C(λ) and C+(λ) partitions based on MDL and the ratio of internal negative (positive) links, useful insights about the role and topological placement of negative ties are obtained (d).
Results
Notation
Throughout the paper, the expressions “link,” “edge,” “tie,” and “relation” are used interchangeably, unless we explicitly make a note. A graph G is determined by the triple (V, E, W) where V is the set of nodes, E is the set of edges defined by pair (vi, vj) of nodes ((vi, vj) = (vj, vi) for undirected graphs) and W assigns a weight to each edge. The induced graph of node set a is defined by (V′, E′, W′) where i) V′ = a, ii) (vi, vj) ∈ E′, if vi, vj ∈ a and (vi, vj) ∈ E and iii) W′(vi, vj) = W(vi, vj). A partition C assigns each node to a module (i.e., ci is the module of node i). Other basic notations are listed in Table 1.
Tools to explore the community structure of signed networks
In this work, we reformulated the well-known Map Equation L(G, C) for signed networks, which is the minimum expected code length that is required to address each step of a random-walker (also known as Minimum Description Length). The idea is that negative ties should be used in line with the “random walkers are more likely to be trapped inside a community” intuition. Therefore, a negative tie from node i of module ci towards c′ should decrease the probability of going from ci to c′ and conversely, a negative tie towards the inside of ci should increase the probability of escaping from ci. Accordingly, Map Equation was reformulated to account for the negative ties (see Methods). By increasing the amount of external (internal) negative ties, it is expected that the value of MDL decreases (increases). Also, we extended the Constant Potts Model (CPM) to signed networks. CPM explicitly states that the absence of internal positive ties should be punished using a constant parameter λ. In particular, by sliding λ from 0 to 1 (or further), the minimization of CPM results in the extraction of smaller and denser modules16. Utilizing these well-established foundations, our method provided a map spectrum for signed networks, which not only revealed the best partition of a network but also provided useful information about negative ties on different scales of a network.
Proposed benchmarks for signed networks
In this manuscript, we extended the LFR (Lancichinetti-Fortunato-Radicchi17) benchmark to signed graphs. As the main characteristic, our extensions (the same as original LFR) provide scale-free distributions for positive (negative) degrees and community sizes. These benchmarks are denoted as signed and coupled LFR. The signed LFR simply replaces internal (or external) positive ties with negative ones. This extension was used to evaluate the effect of external (internal) negative ties on the extended Map Equation. However, in order to evaluate the power of signed detectors, a network must have two features: (1) a valid ground-truth for comparison and (2) informative negative ties, which ignoring them leads to incorrect partitioning. These features do not simultaneously hold for the signed LFR and thus, the coupled LFR was proposed. To show the failure of the signed LFR, the evaluation was started with uninformative negative ties, which can be ignored. Gradually, by placing positive ties between the communities, it was expected that at some point the negative ties become decisive, which means the unsigned detectors unlike signed ones must fail to detect the correct partition. However, before the total collapse of the ground-truth, this did not happen, signifying that the signed LFR has either uninformative negative ties or invalid ground-truth (Fig. 2a). Accordingly, the coupled LFR was introduced. Without going into details, it is composed of two identical LFR graphs and the merging process occurs only between twin (duplicate) communities (Fig. 2b). As the schematic representation shows, the coupled LFR provides an interval (phase 3) with both informative negative ties and known ground-truth, suitable for evaluating the efficiency of signed detectors. The procedure of creating the benchmarks is as follows:
Characteristics of the proposed benchmarks.
Csingle (Ccouple) partition places each community of ground-truth (and its duplicate) in one module. (a) in signed LFR, for any arbitrary amount of external negative ties, by increasing positive ties between communities, the ground-truth is detectable by unsigned methods, as well as signed ones, until it fades out. (b) in coupled LFR, the duplicate (twin) communities are first intertwined with positive ties (phase 1 and 2) and then get separated by negative ties (phase 2 and 3). This leads to (A) a constantly known ground-truth (green double-line) which switches from Csingle to Ccouple and again back to Csingle and (B) informative negative ties in phase 3 where unsigned methods wrongly prefer Ccouple to Csingle. The transition points are illustrated using MDL measure (lower value corresponds to better partition).
Signed LFR
LFR benchmark was extended by introducing external or internal negative ties regarding each node. For the case of external ones, there is an additional parameter  , where
, where  , that forces each node to have
, that forces each node to have  . For example, in a graph with μout = 0.6 and
. For example, in a graph with μout = 0.6 and  , regarding each node i, approximately 40% of links are positive and inside module ci, 25% are negative and outside ci and 35% are positive and outside ci. For the case of internal negatives, using parameter
, regarding each node i, approximately 40% of links are positive and inside module ci, 25% are negative and outside ci and 35% are positive and outside ci. For the case of internal negatives, using parameter  , the procedure is the same as the external ones.
, the procedure is the same as the external ones.
Coupled LFR
This benchmark was built using two identical unsigned LFR graphs that were intertwined using parameters μc and  , where 0 ≤ μc < 1 and
, where 0 ≤ μc < 1 and  . Thus, there are two layers of graphs where each node or community has a duplicate (or twin) in the other one. Keeping the layers unchanged, the benchmark forces node i to have
. Thus, there are two layers of graphs where each node or community has a duplicate (or twin) in the other one. Keeping the layers unchanged, the benchmark forces node i to have  new links towards twin community c’i (similar for
new links towards twin community c’i (similar for  ). That is, by increasing μc, twin communities become intertwined and conversely, by increasing
). That is, by increasing μc, twin communities become intertwined and conversely, by increasing  they become separated. However, the nominal μc may not be satisfied for some nodes and thus, the empirical average was reported in the plots. It is worth mentioning that the “twin” notion is not a model of real-world networks, but an easy way of controlling the network structure to produce informative ties (Fig. 2b). In other words, by introducing the coupled LFR, we tried to ensure the effectiveness when negative ties are playing a decisive role in partitioning the network as well as to include some basic characteristics of real-world networks such as scale-free community sizes and node degrees.
they become separated. However, the nominal μc may not be satisfied for some nodes and thus, the empirical average was reported in the plots. It is worth mentioning that the “twin” notion is not a model of real-world networks, but an easy way of controlling the network structure to produce informative ties (Fig. 2b). In other words, by introducing the coupled LFR, we tried to ensure the effectiveness when negative ties are playing a decisive role in partitioning the network as well as to include some basic characteristics of real-world networks such as scale-free community sizes and node degrees.
Comparison of partitions
The distance between two partitions C and C′ was measured using Normalized Variation of Information (NVI). NVI is zero if the partitions are identical and one if they are statistically independent, meaning no information is gained about C by knowing C′ and vice versa; see the formulation in Methods.
The notations used for denoting general types of partitions are as follows:
-
Ctruth: ground-truth partition of a graph for [un]signed LFR.
-
CAllin1: all-in-one partition, which places all the nodes in one module.
-
Csingle: places each community of coupled LFR in one module.
-
Ccouple: places each community and its twin in one module.
Evaluation of SiMap
In order to investigate the effect of negative ties, SiMap was examined on signed LFR. In Fig. 3a,b, the internal structure of the communities was kept constant during the increase of mixing μout and similarly, the external links were kept constant during the increase of internal ties (μin) in Fig. 3c. As shown in Fig. 3a, for a network of two communities, when the mixing of only positive ties was increased, the value of MDL (solid curve) increased accordingly, which corresponds to the decrease of quality of communities. Next, we stopped adding positive ties at  and started adding negative ones afterwards, where
and started adding negative ones afterwards, where  . The external negative ties are expected to cancel out the positive ones and thus the quality of communities increases again (equally MDL decreases) almost to that of μout = 0. This expectation was validated using different starting points (dashed curves in Fig. 3a). On the other hand, for a network of more than two communities, randomly-added external negative ties may not cancel the positive ties from each node towards every community. In other words, even if
. The external negative ties are expected to cancel out the positive ones and thus the quality of communities increases again (equally MDL decreases) almost to that of μout = 0. This expectation was validated using different starting points (dashed curves in Fig. 3a). On the other hand, for a network of more than two communities, randomly-added external negative ties may not cancel the positive ties from each node towards every community. In other words, even if  , a node may have more positive ties toward a module than negative ones. Hence, as depicted in Fig. 3b, MDL dropped towards the level of μout = 0 with a slower slope and never reached that level. This is consistent with our formulation, stating that the external negative ties would cancel all the positive ones, if their weight towards every community is, at least, as much as positive ones, otherwise, MDL should be higher than that of μout = 0. For the case of internal negative ties, a similar experiment was carried out. As shown in Fig. 3c, internal negative ties canceled the effect of positive ones and consequently weakened the quality of communities almost to the situation where there had been no ties inside the communities (μin = 0).
, a node may have more positive ties toward a module than negative ones. Hence, as depicted in Fig. 3b, MDL dropped towards the level of μout = 0 with a slower slope and never reached that level. This is consistent with our formulation, stating that the external negative ties would cancel all the positive ones, if their weight towards every community is, at least, as much as positive ones, otherwise, MDL should be higher than that of μout = 0. For the case of internal negative ties, a similar experiment was carried out. As shown in Fig. 3c, internal negative ties canceled the effect of positive ones and consequently weakened the quality of communities almost to the situation where there had been no ties inside the communities (μin = 0).
SiMap on signed LFR.
(a) Network of two communities of size 500. We added the external positive ties until  and the negative ties afterwards. Networks with
and the negative ties afterwards. Networks with  had almost the same quality as the case with
had almost the same quality as the case with  . (b) Network of many communities with NG = 1000; although
. (b) Network of many communities with NG = 1000; although  , the external negative ties may not cancel the positive flow from each node towards every community; therefore, dashed MDL curves dropped slowly and never reached the level of
, the external negative ties may not cancel the positive flow from each node towards every community; therefore, dashed MDL curves dropped slowly and never reached the level of  . (c) Network of many communities with NG = 1000; the internal negative ties canceled positive ones almost at the same level as
. (c) Network of many communities with NG = 1000; the internal negative ties canceled positive ones almost at the same level as  . Each value was averaged over 25 graph realizations.
. Each value was averaged over 25 graph realizations.
In general, SiMap not only punishes the presence of internal negative ties, but also rewards the external negative ones. Note that the rewarding is module-wise, which means the mesoscopic topology of the network determines the amount of the reward; e.g., if two modules have no positive ties in between, the inter-negative ones add no information and therefore have no effect on MDL.
Map spectrum of CPM(λ)
In this experiment, the SiMap of signed CPM(λ) was plotted to illustrate its well-behaved curve with respect to the distance function NVI(CCPM, Ctruth). For comparison, the statistics of InfoMap (which ignores negative ties) and Modularity were also plotted. As depicted in Fig. 4a, although NVI is aware of the ground-truth partition, MDL curve behaved similarly to NVI, which first smoothly decreased and then slowly increased. Additionally, the minimum of MDL(λ) coincided with the true community structure of the graph. Furthermore, InfoMap reached the same minimum level of MDL, meaning that the negative ties were not informative in this network. On the other hand, at μout = 0.8, MDL(λ) constantly increased from λ = 0 to 1 (Fig. 4c). This indicates that the single-module is preferred to dividing the network into sub-modules, since it has no significant agglomeration of density at this mixing rate16.
MDL spectrum of CPM(λ) on LFR (NG = 5000).
(a,b) MDL and NVI for  ; although
; although  for every node, the community structure is still clear and detectable24. (c,d) MDL and NVI for
for every node, the community structure is still clear and detectable24. (c,d) MDL and NVI for  , where the network has no significant community structure and thus single-module has lower MDL than the case when the network is divided into sub-modules.
, where the network has no significant community structure and thus single-module has lower MDL than the case when the network is divided into sub-modules.
Performance of CPMap on Signed LFR
In this experiment, we compared InfoMap (which ignores the negative ties), CPMap and Modularity on signed LFR for  (unsigned),
(unsigned),  and
and  . In all cases, CPMap performed better than the signed Modularity. As demonstrated in Fig. 5a,b, on unsigned LFR, CPMap performed nearly as well as InfoMap in optimizing equation (15). This suggests that CPM provides a reach set of partitions. For μout ≥ 0.75, CPMap opted for the single-module partition CAllin1, which had a lower MDL than both Ctruth and the output of InfoMap. Nevertheless, according to Fig. 5a,d, there still remains a room for future improvements upon CPM to optimize SiMap. In Fig. 5c,d, by adding
. In all cases, CPMap performed better than the signed Modularity. As demonstrated in Fig. 5a,b, on unsigned LFR, CPMap performed nearly as well as InfoMap in optimizing equation (15). This suggests that CPM provides a reach set of partitions. For μout ≥ 0.75, CPMap opted for the single-module partition CAllin1, which had a lower MDL than both Ctruth and the output of InfoMap. Nevertheless, according to Fig. 5a,d, there still remains a room for future improvements upon CPM to optimize SiMap. In Fig. 5c,d, by adding  negative ties to each node, even InfoMap was still capable of detecting Ctruth before
negative ties to each node, even InfoMap was still capable of detecting Ctruth before  . After this threshold, all detectors failed to detect Ctruth, since the community structure was not valid anymore due to severe rewirings16,18. In Fig. 5e,f, by adding more negative ties (
. After this threshold, all detectors failed to detect Ctruth, since the community structure was not valid anymore due to severe rewirings16,18. In Fig. 5e,f, by adding more negative ties ( ), although CPMap reached a better MDL than all other partitions, the situation remained almost the same, that is signed LFR either has non-informative negative ties or invalid Ctruth.
), although CPMap reached a better MDL than all other partitions, the situation remained almost the same, that is signed LFR either has non-informative negative ties or invalid Ctruth.
Evaluation of methods on signed LFR (μout is plotted in percentage).
(a,b) NVI and MDL of the algorithms for unsigned LFR, (c,d) NVI and MDL for  and (e,f) for
and (e,f) for  . In all cases, CPMap and InfoMap had close performance and both outperformed Modularity. Before
. In all cases, CPMap and InfoMap had close performance and both outperformed Modularity. Before  ≃ 0.75, all detectors similarly performed on signed LFR as compared to the unsigned one. Roughly for
≃ 0.75, all detectors similarly performed on signed LFR as compared to the unsigned one. Roughly for  , the community structure faded out and all detectors suddenly failed. Therefore, the signed LFR has either non-informative negative ties or invalid Ctruth. Each value was averaged over 25 graph realizations with NG = 5000.
, the community structure faded out and all detectors suddenly failed. Therefore, the signed LFR has either non-informative negative ties or invalid Ctruth. Each value was averaged over 25 graph realizations with NG = 5000.
As a summary, although this benchmark may be first to come to mind, we showed it is not capable of appropriately challenging the signed detectors. The non-informativeness comes from the fact that flipping the external positive links to negative makes the community structure more clear and thus InfoMap performs on signed LFR as accurate as the unsigned one. For this reason, the coupled LFR was introduced that gives us more leverage on the informativeness of negative ties while keeping the community structure valid.
Performance of CPMap on Coupled LFR
In this experiment, using coupled LFR, we investigated the ability of CPMap on utilizing the negative ties’ information. To this end, μout =0.3 was used for each layer to have connected yet well-separated communities and only the connectivity of twin communities was manipulated. First, in Fig. 6a,b, two identical layers of graphs were gradually coupled only with negative ties ( ). As expected, the output of CPMap and InfoMap constantly resembled Csingle, since the negative ties added no competing information to the community structure of positive subgraph. However, the output of Modularity, surprisingly, changed with the increase of negative ties. In particular, by increasing μc, previously detected modules were expanded to form larger ones. In other words, the number of negative ties indirectly weakened the sensitivity of Modularity to the density of positive ties, leading to larger and sparser modules.
). As expected, the output of CPMap and InfoMap constantly resembled Csingle, since the negative ties added no competing information to the community structure of positive subgraph. However, the output of Modularity, surprisingly, changed with the increase of negative ties. In particular, by increasing μc, previously detected modules were expanded to form larger ones. In other words, the number of negative ties indirectly weakened the sensitivity of Modularity to the density of positive ties, leading to larger and sparser modules.
Evaluation of methods on coupled LFR (μc is plotted in percentage).
(a,b) Only negative ties were added between two layers. Csingle constantly had the lowest MDL and was detected by InfoMap and CPMap. However, the Modularity failed to detect Csingle by merging its communities. (c,d) Positive ties were added between twin communities until  and negative ties were added afterwards. CPMap constantly preferred the structure with the lowest MDL that is, in order, Csingle, Ccouple and again Csingle. However, InfoMap wrongly preferred Ccouple after
and negative ties were added afterwards. CPMap constantly preferred the structure with the lowest MDL that is, in order, Csingle, Ccouple and again Csingle. However, InfoMap wrongly preferred Ccouple after  , signifying the usefulness of negative ties. (e,f) The experiment was repeated using more intertwined layers at
, signifying the usefulness of negative ties. (e,f) The experiment was repeated using more intertwined layers at  . For all cases, Modularity reacted slowly to informative ties and eventually failed to detect Csingle. Each value was averaged over 25 graph realizations with Neach layer = 5000.
. For all cases, Modularity reacted slowly to informative ties and eventually failed to detect Csingle. Each value was averaged over 25 graph realizations with Neach layer = 5000.
Second, in Fig. 6c–f, the amount of positive ties  between twin communities was increased until the quality of Ccouple surpassed that of Csingle. At this point, Ccouple was preferred by the detectors instead of Csingle. Knowing that CPMap and Modularity are partitioning the networks based on a criteria other than SiMap, this somehow validated the alignment of SiMap with the true quality of partitions. In the next phase, the negative ties
between twin communities was increased until the quality of Ccouple surpassed that of Csingle. At this point, Ccouple was preferred by the detectors instead of Csingle. Knowing that CPMap and Modularity are partitioning the networks based on a criteria other than SiMap, this somehow validated the alignment of SiMap with the true quality of partitions. In the next phase, the negative ties  were added between twin communities to break them apart. As a result, the negative ties gradually became informative, since by ignoring them, InfoMap kept partitioning the graph exactly the same as Ccouple. When Csingle surpassed Ccouple, CPMap started to switch from Ccouple to Csingle accordingly. However, this switching occurred much later for the signed Modularity, meaning that it is less sensitive to the informative negative ties. Also, it never opted for Csingle due to an inherent inconsistency. Nevertheless, there is still a room for improvement upon signed CPM for optimizing SiMap, which is evident from 0.3 < μc < 0.45 in Fig. 6c,d and 0.45 < μc < 0.55 in Fig. 6e,f, where MDLsingle is better than MDLCPM.
were added between twin communities to break them apart. As a result, the negative ties gradually became informative, since by ignoring them, InfoMap kept partitioning the graph exactly the same as Ccouple. When Csingle surpassed Ccouple, CPMap started to switch from Ccouple to Csingle accordingly. However, this switching occurred much later for the signed Modularity, meaning that it is less sensitive to the informative negative ties. Also, it never opted for Csingle due to an inherent inconsistency. Nevertheless, there is still a room for improvement upon signed CPM for optimizing SiMap, which is evident from 0.3 < μc < 0.45 in Fig. 6c,d and 0.45 < μc < 0.55 in Fig. 6e,f, where MDLsingle is better than MDLCPM.
Online Social Media Networks
Using the proposed tools, we investigated the mesoscopic structure of three well-known real signed networks: Slashdot, Epinions and WikiElections. To this end, we optimized equation (17) for the whole spectrum of λ = [0, 1] and further analyzed the corresponding partitions at each scale (only the informative intervals are plotted). In particular, the main information comes from comparing the spectrum of signed CPM to that of CPM+, which is only applied on the positive subgraph, to find the role of negative ties in different scales of the network. Also, this spectrum of partitions were compared with the output of InfoMap and signed Modularity.
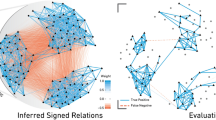
As depicted in Figs 7, 8 and 9, MDL curve was V-shaped for all three networks with a minimum at λmin, which signifies that i) the networks have community structure and ii) the best map of each network is made up of modules with density ≃λmin or higher that are mutually connected with the same density or lower. In particular, WikiElections had considerably denser modules than both Slashdot and Epinions, which is consistent with its relatively higher density of positive ties (see Table 2). Also, regarding the internal negative (positive) ties, they continuously declined and were placed between the modules, as the interpretation of λ suggests.
Mesoscopic spectrum of Slashdot dataset.
MDL, Hλ(G, C) and the ratio of internal negative (positive) ties are plotted for the output of CPM(λ), CPM+(λ), InfoMap and signed Modularity. λmin marks the best scale for CPM at which it has the lowest MDL. CPM+ is the application of CPM on positive subgraph. If the output of CPM has lower (better) H than that of CPM+, the value of inset will be 1 and 0 otherwise.
Mesoscopic spectrum of Epinions dataset.
Designations are as Fig. 7.
Mesoscopic spectrum of WikiElections dataset.
Designations are as Fig. 7.
Slashdot
According to Fig. 7, in all scales, the MDL curve of CPM+ was better than that of CPM. Also, MDL of InfoMap was better than MDL(λmin) of CPM. Although the optimized value of equation (17) was slightly better for CPM than CPM+, which implies the constructive role of the negative ties in the optimization process, better MDL of both CPM+ and InfoMap signified that negative ties were not informative to achieve a higher quality mesoscopic structure as compared to the coupled LFR. Also, in terms of the internal negative ties, CPM+ placed them between modules after λ ≃ 0.015 without using their information, implying that almost all (95%) of negative ties were naturally placed between modules of density ≃0.015 or higher that were mutually connected with the same density or lower. These findings are consistent with previous ones both on microscopic19 and mesoscopic levels20. However, using the proposed tools, one captures a more quantitative picture of negative ties for the entire spectrum of the mesoscopic structure.
Epinions
According to Fig. 8, similar to Slashdot, CPM+ and InfoMap reached a better MDL than CPM, meaning that one could not find a better partition by taking negative ties into account. However, CPM+ could not exclude 95% of negative ties until λ ≃ 0.085. Therefore, the negative ties are placed between the modules of higher density with stronger interconnections compared to Slashdot. This means that the “negative ties lie between dense positive modules” pattern is apparent, yet, less salient than Slashdot.
WikiElections
According to Fig. 9, unlike Slashdot and Epinions, CPM had considerably better MDL than both CPM+ and InfoMap at the best scale λmin = 0.0029 and beyond until λ ≃ 0.1. This suggests that the information of negative ties is useful for WikiElections and only vanishes when one zooms into the network to find the modules of density ≃ 0.1 or higher. Accordingly, negative ties lose their informativeness for λ ≥ 0.1. However, this threshold is well before the trivial case λ ≃ 1, where the objective is merely to find positive cliques. Additionally, CPM+ could not place 95% of negative ties between the modules until λ ≃ 0.25, meaning that the position of negative ties between dense positive ones is considerably less notable than Slashdot and Epinions. It is worth mentioning that Leskovec et al. also observed this different pattern of relations from local perspective, which have resulted in a weak cross-generalization of link prediction models and also less accurate models for WikiElections21.
Indeed, these observations can be explained using the intuitive information trade-off of negative ties between local level (for sign prediction) and mesoscopic level (for community detection). That is to say, the more principled the negative ties between dense positive regions, the more accurate a link type can be predicted given the information of its neighbors and conversely, the less information they have for the task of community detection20.
More on Signed Modularity
Based on the results from coupled LFR, by increasing the negative ties, Modularity loses its sensitivity to the density of positive ties. Moreover, our experiments showed that even if two layers of coupled LFR are connected by only negative ties, again, the increase of negative ties leads to placing each layer in one module (Fig. 10b). Note that the coupled LFR is used to resemble two positive regions of a network (with heterogeneous densities internally) that are connected by negative ties. As an attempt to explain this observation, we considered a coupled LFR with fixed parameter μout, which controls the mixing of each layer and tunable parameter μc, which adds [only] negative ties between two layers. Setting  , the amount of negative ties relative to positive ones is
, the amount of negative ties relative to positive ones is

and the sum of positive/negative ties from each module is

Hence, Q can be rewritten in module terms as follows:

where  is a constant value. According to the interpretation provided in Methods, the functionality of
is a constant value. According to the interpretation provided in Methods, the functionality of  , similar to
, similar to  , is to control the density of modules. Therefore, by increasing q, this sparsity-punishment term is attenuated and consequently, modules try to gather more links ignoring the loss of density. That is to say, the density of each module gradually becomes less important and conversely, the number of internal links becomes more important, which leads to larger and sparser modules consistent with our experiments (Fig. 11). In the same way, equalizing the importance of positive and negative ties (α = 0.5) leads to an even worse situation as:
, is to control the density of modules. Therefore, by increasing q, this sparsity-punishment term is attenuated and consequently, modules try to gather more links ignoring the loss of density. That is to say, the density of each module gradually becomes less important and conversely, the number of internal links becomes more important, which leads to larger and sparser modules consistent with our experiments (Fig. 11). In the same way, equalizing the importance of positive and negative ties (α = 0.5) leads to an even worse situation as:
Size of the largest module of Modularity on coupled LFR (μc is plotted in percentage).
For  , by increasing the number of negative ties between two identical LFR graphs (which have a clear community structure at
, by increasing the number of negative ties between two identical LFR graphs (which have a clear community structure at  ), modules were expanded until each layer of 5000 nodes was enclosed in one module. This happened after
), modules were expanded until each layer of 5000 nodes was enclosed in one module. This happened after  corresponding to
corresponding to  . For α = 0.5, complete expansion occurred right after a slight deviation from μc = 0. The graphs were averaged over 25 realizations with Neach layer = 5000.
. For α = 0.5, complete expansion occurred right after a slight deviation from μc = 0. The graphs were averaged over 25 realizations with Neach layer = 5000.

implying that, for any q > 0, the objective is to have higher (lower) number of positive (negative) ties regardless of the density. This was revealed by our experiments which showed that each layer was placed into one module by a slight increase in μc (Fig. 11). In fact, we argue that the reason for this failure is due to the implicit scale of Modularity that is similar for both positive and negative subgraphs. Setting λ− = λ in equation (16), this becomes more clear as follows:

which basically leads the signed CPM to the same drawback as Modularity.
It can be concluded that when the number of negative ties increases, the sensitivity of Modularity to the density of positive ties deceases as the objective merely becomes grouping higher number of positive ties while excluding the negative ones, which is similar to Correlation Clustering. This inconsistency is resolved for CPM by setting λ− = 0 (see Methods).
Discussion
In this work, we resolved the problem of community detection in networks with positive and negative edges. The proposed algorithm showed an excellent performance on novel synthetic benchmarks. Moreover, it provided a mesoscopic spectrum of signed networks, giving novel insights into the informativeness of negative ties as well as their topological placement between dense positive regions. Hence, one can attain a profound understanding about the structural relevance of positive and negative relations and utilize that to justify the absorptive-repulsive behavior of the entities according to the context.
The proposed algorithm, CPMap, showed a reasonable performance close to InfoMap on unsigned networks and non-informative signed networks, outperforming signed Modularity. Also, when the negative ties were informative, CPMap performed excellent, extending the capabilities of InfoMap to signed networks. On the contrary, signed Modularity showed considerably weaker sensitivity to the presence of informative negative ties, as well as, growing inconsistency when the relative number of negative ties was increased. This inconsistency was further justified by the physical interpretation of the scale parameter λ, shedding new light on the general form of signed objectives.
Regarding the mesoscopic spectrum of real-world networks, we observed that negative ties in Slashdot and Epinions did not contribute to a better quality map than positive subgraph. However, they were informative for extracting the best map of WikiElections, where both CPM+ and InfoMap reached a similar MDL, yet, considerably worse than signed CPM. This usefulness lasted until we zoomed into the network to find the modules of density ≃0.1 or higher. Moreover, the placement of negative ties between dense positive modules was more prominent in Slashdot and Epinions than WikiElections. However, this obscure pattern in WikiElections led to the extraction of more information from negative ties for community detection, consistent with the lower information extracted for the task of sign prediction21. Considering the nontrivial position of negative ties, if one wishes to detect modules of maximum density, i.e., positive cliques, negative ties obviously play no role in the detection task and they are always placed between the modules. However, for Slashdot/Epinions/WikiElections, the majority of the negative ties were between modules of density ≃0.015/0.085/0.25 or higher that were interconnected with the same density or lower, well before this trivial case. Therefore, we showed that it is expected to observe the “negative ties lie between dense positive ties” pattern in a nontrivial setting for real-world networks.
Methods
Tools to explore the community structure of signed networks
We first introduce two objective functions used to determine the quality of communities: Map Equation22 and Constant Potts Model23, which been previously used for unsigned graphs. We reformulated the Map Equation to signed networks (SiMap) by reweighting the walking patterns based on the mesoscopic information of negative ties. Also, we extended CPM to signed graphs, which remains unchanged when the same weight is used for both negative and positive terms. For the final algorithm, the only parameter of signed CPM, λ, is determined using SiMap.
Map Equation
Given a graph G and a partition C, Map Equation L(G, C) is the minimum expected code length that is required to address each step of a random-walker. Suppose a random-walker is going from node n to n′, this step is addressed as follows:
-
1
If the walker stays inside module c, a code is produced for n′.
-
2
If the walker goes from module c to c′, an exit-code for c, a code for c′ and finally a code for n′ are produced sequentially.
Accordingly, there are two levels of coding. In the first level a code is assigned to each module and in the second level each module receives a private coding for members and the action of exiting the module. Finally, using Shannon entropy, the theoretical minimum code length is achieved when the codes are assigned to entities based on their frequency of use. Consequently, the calculation of Map Equation is narrowed down to the relative frequency of visiting nodes and entering-exiting modules. Recent studies have shown that L is a very powerful criterion for detection of community structures, both experimentally24,25,26 and theoretically27.
Constant Potts Model (CPM)
To overcome the well-known resolution limit of modularity-alike objectives, Traag et al.23 suggested an objective function known as Constant Potts Model (CPM) as:

where λ is a constant value. This equation can be rewritten in modular terms as:

Theoretically, CPM has a clear interpretation based on λ23; H rewards module c with density  larger than λ and punishes c otherwise. H prefers modules r and s being separated if they have inter-density
larger than λ and punishes c otherwise. H prefers modules r and s being separated if they have inter-density  smaller than λ and merges them otherwise. We used this interpretation to extend CPM to signed graphs and to analyze real-world networks. Although CPM has a simple formulation, it shows an outstanding performance on the state-of-the-art benchmarks if a proper λ is known a priori23. However, the burden of community detection is on parameter λ. One can get a wide range of partitions from all-in-one to each-in-one by sliding λ from 0 to 1 (and even further for weighted graphs). In other words, by increasing λ, we zoom into the network to see smaller, denser groups that are interconnected more densely. Consequently, the optimal value of λ is a fundamental key to the success of the method.
smaller than λ and merges them otherwise. We used this interpretation to extend CPM to signed graphs and to analyze real-world networks. Although CPM has a simple formulation, it shows an outstanding performance on the state-of-the-art benchmarks if a proper λ is known a priori23. However, the burden of community detection is on parameter λ. One can get a wide range of partitions from all-in-one to each-in-one by sliding λ from 0 to 1 (and even further for weighted graphs). In other words, by increasing λ, we zoom into the network to see smaller, denser groups that are interconnected more densely. Consequently, the optimal value of λ is a fundamental key to the success of the method.
Map Equation for signed networks (SiMap)
According to the proposed idea, the information of negative ties should affect the flowing pattern of a random-walker. As a result, given a graph G and a partition C, the weight (selection probability) of positive ties from node i of module ci towards module c′ is first decreased proportional to the negative ties from i towards c′ and then the remaining probability (pi, back) is channeled back to the internal links. Hence, if a random-walker arrives at node i, it is less likely to select the links toward module c′ and more likely to step back inside ci. After this, the weight of internal positive ties is decreased proportional to the internal negative ties and finally, the remaining probability (negative teleport  ), which has been subtracted from the internal positive ties, is uniformly split upon all the nodes in the network. As a summary, in the presence of external negative ties, a walker is less likely to leave ci and conversely, due to internal negative ties, it is more likely to escape from ci by choosing a random node outside ci.
), which has been subtracted from the internal positive ties, is uniformly split upon all the nodes in the network. As a summary, in the presence of external negative ties, a walker is less likely to leave ci and conversely, due to internal negative ties, it is more likely to escape from ci by choosing a random node outside ci.
Generally, the reweighting process is a heuristic choice. Nonetheless, one can simply make the following assumptions: i) if the weight of negative ties toward c′ is at least the same as positive ties, the walker should not go to c′ and ii) if the same situation holds for the links toward the inside of ci, the walker should not directly step back inside ci. Based on these, we propose the following reweighting formulation:

where reweighted (teleport-free) probabilities are

and the negative teleportation from each node is

which depends on the backward flow calculated as

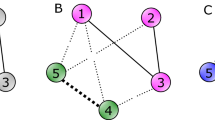
To be cleared, two examples of the procedure, which is applied on a sample node, are provided in Fig. 12. As a special case, if there is no negative tie, all transition probabilities remain unchanged.
Application of the reweighting procedure on node 1.
(a) Neighborhood of node 1 in a signed network. (b) The flow pattern of positive subgraph from node 1, which is used in the unsigned Map Equation. (c) Node 1 has the same amount of negative and positive ties towards c2, thus, all the flow is channeled back into c1. (d) All the flow towards c2 is channeled back into c1, the flow towards c3 remains unchanged and 3/8 of flow is uniformly spread over the network due to internal negative tie 1 → 3, which increases both the disorderedness of flow and the probability of escaping from c1.
Now, the probabilities of visiting nodes and entering (or exiting) modules need to be calculated. Note that a graph must be ergodic in order to have a stationary visiting distribution. The ergodicity is guaranteed by the use of teleportation that is being at node i, a random-walker either teleports to node j with probability τ  j where
j where  , or selects link from node i to j with probability
, or selects link from node i to j with probability  28. Moreover, in an ergodic graph the probability of entering or exiting a module is the same. The probability of visiting node i in the reweighted graph G′ can be recursively calculated as:
28. Moreover, in an ergodic graph the probability of entering or exiting a module is the same. The probability of visiting node i in the reweighted graph G′ can be recursively calculated as:

Since the graph is ergodic, starting with an arbitrary distribution, e.g.,  , equation (13) converges to the true visiting probabilities [Empirically, distance
, equation (13) converges to the true visiting probabilities [Empirically, distance  drops to 10−15 after around 100 iterations on a graph with 106 links.]. Having pi calculated for each node i, the exiting (or entering) probability of a module c is:
drops to 10−15 after around 100 iterations on a graph with 106 links.]. Having pi calculated for each node i, the exiting (or entering) probability of a module c is:

As a special case, if there is no negative tie and the teleportation is uniform  , equation (14) is the same as the one derived in28.
, equation (14) is the same as the one derived in28.
Having equations (13 and 14) as the main ingredients, the extended Map Equation (SiMap) is calculated as:

where  is the probability of using a first-level code and
is the probability of using a first-level code and  is the probability of using the second-level code of module c. Knowing that we encapsulated the information of negative ties in pi and Qc, equation (15) is the same as that of unsigned graphs28.
is the probability of using the second-level code of module c. Knowing that we encapsulated the information of negative ties in pi and Qc, equation (15) is the same as that of unsigned graphs28.
Smart teleportation
Lambiotte and Rosvall29 showed that although teleportation probability τ rectifies the instability of the visiting distribution, it may considerably bias the results. As a solution, they effectively resolved this biased behavior of Map Equation by: 1) setting  , 2) setting τ = 0 in equation (14) and 3) iterating equation (13) one extra step using τ = 0. In this work, after the reweighting procedure, we did the same for calculation of equations (13 and 14).
, 2) setting τ = 0 in equation (14) and 3) iterating equation (13) one extra step using τ = 0. In this work, after the reweighting procedure, we did the same for calculation of equations (13 and 14).
CPM for signed graphs
According to the extension of modularity-alike functions to signed graphs14, CPM can be extended as:

which introduces a new parameter λ−. In the same work, Traag and Bruggeman manually set non-zero values for parameters λ and λ− to highlight their importance. Nevertheless, we argue that λ− must be set to 0 for the case of CPM. The reason lies in the qualitative objective that is to detect “dense positive” and “negative-free” modules. In particular, “negative-free” condition can be restated as: any density of internal negative ties must be punished. However, according to the interpretation of λ, if density of the negative ties inside a module c is at most λ−, c receives an extra reward from equation (16). This implies that the internal negative ties wrongly increase the quality of c compared to the case when they are completely ignored. Therefore, by setting λ− =0, any amount of internal negative ties is punished. Also, if α is set to 0.5 (equal contribution for positive and negative terms), both signed and unsigned CPM objectives will be the same, which only differ in multiplicative constant 0.5:

Intuitively, α is set to 0.5 to have a certain amount of positive ties being canceled out by the same amount of negative ones. Nonetheless, depending on the application, if intrinsic value of positive ties differ from negative ones, their weights must be set accordingly prior to applying the algorithm.
To optimize CPM, we use an improved version of Louvain method devised by Rosvall and Bergstrom, which is also the one utilized in InfoMap30. Louvian method first assigns a unique label to each node, then expands each label to those neighbors that maximally improve the objective value and finally folds each module into a node and repeats the procedure until no further improvement is made31. The improved procedure first runs the Louvain algorithm and then recursively refines both the nodes and modules to enhance the objective value further30. In our experiments, after 3 to 4 refinements the objective value was not considerably improved. Furthermore, the same procedure is used for the Modularity so as to eliminate the potentially biased comparisons due to different optimization procedures.
The main ingredient of Louvain method is the local-update formula31. Considering the unsigned CPM, when a set of nodes κ is moved from module c to c′, the local update becomes as23:

where κ is considered in both c and c′ for calculating Nc and Nc′. For the case of signed CPM, the extension is straightforward as:

reminding that λ is set to zero for the negative subgraph. Regarding equation (19), the positive and negative subgraphs are treated separately during the optimization process.
Constant Potts Map (CPMap)
SiMap cannot be optimized via local methods of Louvain type, since a local change in a partition costs in the order of total links rather than local links. Indeed, the selection probability of positive ties must be updated according to the new position of negative ties and thus the stationary distribution needs to be recalculated using equation (13). Nevertheless, SiMap still can be used to select among a set of candidate partitions. In particular, SiMap is used to find the best map of a network among the partitions provided by signed CPM. As Traag et al. showed, CPM provides a spectrum of maps that goes from highly simplified to highly detailed by sliding λ from 0 to 116. Hence, as the main goal of Map Equation suggests22, one can use SiMap to select a map that balances between abridgment and expatiation, while constrained to the “negative free” condition.
Consequently, the proposed algorithm (CPMap) first feeds a set of λs to equation (17), then minimizes the equation to get the corresponding partitions and finally outputs the one with the lowest SiMap. Candidate λs indeed can be chosen in a number of heuristic ways. However, in the experiments, we had the following observations: i) for a network with clear community structure, going from λ = 0 to λ ≈ 0.1, the MDL curve smoothly dropped and it slowly rose by further increasing λ and ii) for a network with no community structure, the MDL curve rose at the beginning of sliding λ away from 0, which means grouping the network as a whole was preferred to dividing it. Based on these observations, the following λ-selection is proposed:
-
1
Set
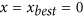 and
and  .
. -
2
If
 , output the partition of
, output the partition of 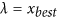 .
. -
3
Consider N + 1 equally spaced λs in
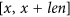 . For newly added ones, optimize equation (17) and calculate MDL of corresponding partitions,
. For newly added ones, optimize equation (17) and calculate MDL of corresponding partitions,-
a
If MDL(x) is the minimum, output the partition of λ = x.
-
b
Else if
 is the minimum, set
is the minimum, set 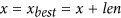 , then go to (2).
, then go to (2). -
c
Else if MDL(x′) is the minimum, set xbest =x′,
 and
and  , then go to (2).
, then go to (2).
-
a
In the experiments, we set N = 4 and L = 0.005; since the MDL curve had smooth changes, either increasing N or decreasing L did not considerably improve the results.
Normalized Variation of Information (NVI)
This metric32 measures the distance between two partitions, which is defined as:

where H(.|.) is the conditional entropy, and

where  denotes the module of node i in partition κ. In particular, given one partition, NVI measures the remaining uncertainty about the other one. For example, if C1 = C2, given one partition, there is no uncertainty about the other one and thus NVI(C1, C2) = 0. NVI is also closely related to Normalized Mutual Information (NMI)33; however, NVI is a metric32 and has a clear interpretation34.
denotes the module of node i in partition κ. In particular, given one partition, NVI measures the remaining uncertainty about the other one. For example, if C1 = C2, given one partition, there is no uncertainty about the other one and thus NVI(C1, C2) = 0. NVI is also closely related to Normalized Mutual Information (NMI)33; however, NVI is a metric32 and has a clear interpretation34.
Common parameters of benchmarks
The parameters for artificial benchmarks were set as: γ = 1, β = 2,  ,
,  ,
,  and
and  . Moreover, regarding the other frequently used settings24, the conclusion drawn from each experiment remains the same.
. Moreover, regarding the other frequently used settings24, the conclusion drawn from each experiment remains the same.
Online Social Networks and Data preprocessing
We analyze three widely studied online signed social networks: Slashdot, Epinions and WikiElections21. These datasets have been frequently used as benchmarks for studying signed social relations [All datasets are publicly available at http://snap.stanford.edu. For more detailed statistics refer to http://konect.uni-koblenz.de/]. They have special characteristics that make them suitable for the analysis of social relations. For example, all of the links either positive (for friendship or trust) or negative (for enmity or distrust) have been explicitly established by users, which means none of them has been inferred indirectly or asked from a person.
We performed some preprocessings on these datasets making them suitable for our purpose:
-
1
In order to get an undirected network, reciprocal links with inconsistent signs were omitted and the remaining links were considered as undirected (inconsistent relations were 0.4%, 0.7% and 1.6% of relations in Slashdot, Epinions and WikiElections, respectively).
-
2
Only the largest connected component of each network was considered (99%, 90% and 85% of nodes in Slashdot, Epinions and WikiElections, respectively).
-
3
Nodes incident to zero positive edges were removed as they, trivially, belong to an isolated cluster.
Table 2 summarizes the properties of these networks after the above operations.
Additional Information
How to cite this article: Esmailian, P. and Jalili, M. Community Detection in Signed Networks: the Role of Negative ties in Different Scales. Sci. Rep. 5, 14339; doi: 10.1038/srep14339 (2015).
References
Fortunato, S. Community detection in graphs. Phys. Rep. 486, 75–174 (2010).
Papadopoulos, S., Kompatsiaris, Y., Vakali, A. & Spyridonos, P. Community detection in social media. Data Min. Knowl. Disc. 24, 515–54 (2012).
Newman, M. E. J. & Park, J. Why social networks are different from other types of networks. Phys. Rev. E 68, 036122 (2003).
Backstrom, L., Huttenlocher, D., Kleinberg, J. & Lan, X. Group formation in large social networks: membership, growth and evolution. Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 44–54. Philadelphia, PA, USA: ACM. (2006 August).
Guimera, R. et al. Self-similar community structure in a network of human interactions. Phys. Rev. E 68, 065103 (2003).
Lancichinetti, A., Kivelä, M., Saramäki, J. & Fortunato, S. Characterizing the community structure of complex networks. PloS ONE 5, e11976 (2010).
Onnela, J.-P. et al. Geographic constraints on social network groups. PLoS ONE 6, e16939 (2011).
Grabowicz, P. A. et al. Social features of online networks: The strength of intermediary ties in online social media. PloS ONE 7, e29358 (2012).
Javari, A. & Jalili, M. Cluster-based collaborative filtering for sign prediction in social networks with positive and negative links. ACM Trans. Intell. Syst. Technol. 5, 24 (2014).
Porter, M. A., Onnela, J.-P. & Mucha, P. J. Communities in networks. Notices of the AMS 56, 1082–97 (2009).
Granell, C., Gómez, S. & Arenas, A. Mesoscopic analysis of networks: Applications to exploratory analysis and data clustering. Chaos 21, 016102 (2011).
Bansal, N., Blum, A. & Chawla, S. Correlation clustering. Mach. Learn. 56, 89–113 (2004).
Radicchi, F. et al. Defining and identifying communities in networks. Proc. Natl. Acad. Sci. USA 101, 2658–63 (2004).
Traag, V. A. & Bruggeman, J. Community detection in networks with positive and negative links. Phys. Rev. E 80, 036115 (2009).
Gómez, S., Jensen, P. & Arenas, A. Analysis of community structure in networks of correlated data. Phys. Rev. E 80, 016114 (2009).
Traag, V. A., Krings, G. & Dooren, P. V. Significant scales in community structure. Sci. Rep. 3, 2930 (2013).
Lancichinetti, A., Fortunato, S. & Radicchi, F. Benchmark graphs for testing community detection algorithms. Phys. Rev. E 78, 046110 (2008).
Leskovec, J., Huttenlocher, D. & Kleinberg, J. Signed networks in social media. Proceedings of the SIGCHI Conference on Human Factors in Computing Systems 1361–70. Atlanta, Georgia, USA: ACM. (2010 April).
Esmailian, P., Abtahi, S. E. & Jalili, M. Mesoscopic analysis of online social networks: the role of negative ties. Phys. Rev. E 90, 042817 (2014).
Leskovec, J., Huttenlocher, D. & Kleinberg, J. Predicting positive and negative links in online social networks. Proceedings of the 19th International Conference on World Wide Web 641–50. Raleigh, NC, USA: ACM. (2010 April).
Rosvall, M. & Bergstrom, C. T. Maps of random walks on complex networks reveal community structure. Proc. Natl. Acad. Sci. USA 105, 1118–23 (2008).
Traag, V. A., Dooren, P. V. & Nesterov, Y. Narrow scope for resolution-limit free community detection. Phys. Rev. E 84, 016114 (2011).
Lancichinetti, A. & Fortunato, S. Community detection algorithms: a comparative analysis. Phys. Rev. E 80, 056117 (2009).
Aldecoa, R. & Marn, I. Closed benchmarks for network community structure characterization. Phys. Rev. E 85, 026109 (2012).
Aldecoa, R. & Marn, I. Exploring the limits of community detection strategies in complex networks. Sci. Rep. 3, 2216 (2013).
Orman, K. G., Labatut, V. & Cheri H. Comparative evaluation of community detection algorithms: a topological approach. J. Stat. Mech.: Theory Exp. P08001; 10.1088/1742-5468/2012/08/P08001 (2012).
Kawamoto, T. & Rosvall, M. The map equation and the resolution limit in community. arXiv:1402.4385v1 (2014). Date of access: 04/05/2014.
Rosvall, M., Axelsson, D. & Bergstrom, C. T. The map equation. E.P.J. S.T. 178, 13–23 (2009).
Lambiotte, R. & Rosvall, M. Ranking and clustering of nodes in networks with smart teleportation. Phys. Rev. E 85, 056107 (2012).
Rosvall, M. & Bergstrom, C. T. Fast stochastic and recursive search algorithm. (2009). Available at: www.tp.umu.se/rosvall/algorithm.pdf (Accessed: 7th November 2013).
Blondel, V. D., Guillaume, J.-L., Lambiotte, R. & Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech.: Theory Exp. P10008; 10.1088/1742-5468/2008/10/P10008 (2008).
Meilă, M. Comparing clusterings an information based distance. J. Multivariate Ana l. 98, 873–95 (2007).
Aldecoa, R. & Marn, I. Deciphering network community structure by surprise. PloS ONE 6, e24195 (2011).
Karrer, B., Levina, E. & Newman, M. E. J. Robustness of community structure in networks. Phys. Rev. E 77, 046119 (2008).
Author information
Authors and Affiliations
Contributions
P.E. and M.J. analyzed the map spectrum of signed networks. P.E. formulated/implemented the idea. P.E. and M.J. wrote the manuscript. M.J. reviewed the analysis.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Esmailian, P., Jalili, M. Community Detection in Signed Networks: the Role of Negative ties in Different Scales. Sci Rep 5, 14339 (2015). https://doi.org/10.1038/srep14339
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep14339
This article is cited by
-
Approximation Algorithms on k-Correlation Clustering
Journal of the Operations Research Society of China (2023)
-
Characterizing attitudinal network graphs through frustration cloud
Data Mining and Knowledge Discovery (2021)
-
A simple approach for quantifying node centrality in signed and directed social networks
Applied Network Science (2020)
-
Towards systemic and contextual priority setting for implementing the 2030 Agenda
Sustainability Science (2018)
-
An algorithm based on positive and negative links for community detection in signed networks
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.













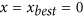 and
and  .
. , output the partition of
, output the partition of 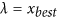 .
.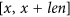 . For newly added ones, optimize equation
. For newly added ones, optimize equation  is the minimum, set
is the minimum, set 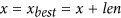 , then go to (2).
, then go to (2). and
and  , then go to (2).
, then go to (2).