Abstract
We report that a ferroelectric-like metallic state with reduced anisotropy of polarization is created by the doping of conduction electrons into BaTiO3, on the bases of x-ray/electron diffraction and infrared spectroscopic experiments. The crystal structure is heterogeneous in nanometer-scale, as enabled by the reduced polarization anisotropy. The enhanced infrared intensity of soft phonon along with the resistivity reduction suggests the presence of unusual electron-phonon coupling, which may be responsible for the emergent ferroelectric structure compatible with metallic state.
Similar content being viewed by others
Introduction
Electric polarization and its coupling with other electronic degrees of freedom in ferroelectrics offer a fertile ground for realizing unconventional quantum phases with unique functionalities. Recent researches uncovered that versatile magnetically/structurally driven ferroelectric phases with magnetoelectric and electromechanical phenomena can be invoked by harnessing the interplay between polarization and spin or crystal-lattice degrees of freedom1,2,3. For examples, the spiral magnetic ordering in Mott insulators often exhibits ferroelectric phases with giant static/dynamical magnetoelectric effects4,5,6,7,8. So far, the design principle to find a new ferroelectric phase has been implicitly limited to insulators, but the concept might be generalized to metals, in which the ‘polarization’, or equivalently, cooperative polar lattice distortion is coupled to mobile charge. In this context, electron doped ferroelectrics may be unique candidates to study the interplay between conduction electron and polarization.
The perovskite BaTiO3 is a prototypical ferroelectric, which is currently utilized in a variety of electronic devices including capacitors, thermistors and nonlinear optical crystals. It shows versatile thermally-induced ferroelectric phases with the macroscopic electric polarization parallel to  ,
,  and
and  axes as characterized by tetragonal, orthorhombic and rhombohetral crystallographic symmetries, respectively (Fig. 1). (Note that the crystal axes are denoted here in cubic notation.) Although pristine BaTiO3 is a band insulator with a gap of about 3.2 eV, it can be turned into a semiconductor or metal by doping conduction electrons into Ti-
axes as characterized by tetragonal, orthorhombic and rhombohetral crystallographic symmetries, respectively (Fig. 1). (Note that the crystal axes are denoted here in cubic notation.) Although pristine BaTiO3 is a band insulator with a gap of about 3.2 eV, it can be turned into a semiconductor or metal by doping conduction electrons into Ti- band by means of chemical substitutions or introduction of oxygen vacancies9,10,11,12. Specifically, the dilutely doped systems with electron concentration (n) less than 1 × 1020 cm−3 are semiconducting and exhibit successive ferroelectric-like phase transitions, which manifest as discontinuous changes in resistivity12. On the other hand, the heavily doped systems are metallic down to low temperatures and the resistivity curve shows more moderate temperature dependence without discontinuous jumps. Figure 2(a) exhibits the typical profile of resistivity for a heavily doped single crystal with n = 1.9 × 1020 cm−3. Here, we partially substituted Ba-ions with La ions for electron doping (See Methods). The resistivity shows a metallic behavior, except a cusp-like anomaly around 260 K and a small upturn due to weak localization below 70 K.
band by means of chemical substitutions or introduction of oxygen vacancies9,10,11,12. Specifically, the dilutely doped systems with electron concentration (n) less than 1 × 1020 cm−3 are semiconducting and exhibit successive ferroelectric-like phase transitions, which manifest as discontinuous changes in resistivity12. On the other hand, the heavily doped systems are metallic down to low temperatures and the resistivity curve shows more moderate temperature dependence without discontinuous jumps. Figure 2(a) exhibits the typical profile of resistivity for a heavily doped single crystal with n = 1.9 × 1020 cm−3. Here, we partially substituted Ba-ions with La ions for electron doping (See Methods). The resistivity shows a metallic behavior, except a cusp-like anomaly around 260 K and a small upturn due to weak localization below 70 K.
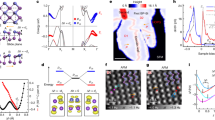
Structural phase diagram and schematic view of the macroscopic polarization in electron doped BaTiO3.
C, T, O, R and M represent cubic, tetragonal, orthorhombic, rhombohedral and monoclinic, respectively. Arrows denote the direction of macroscopic electric polarization (P). P is pointing toward  ,
,  and
and  in tetragonal, orthorhombic and rhombohedral phase, respectively, while that in the ‘monoclinic’ phase does to a certain direction in-between
in tetragonal, orthorhombic and rhombohedral phase, respectively, while that in the ‘monoclinic’ phase does to a certain direction in-between  and
and  direction within
direction within  plane. The shaded plane indicates
plane. The shaded plane indicates  plane.
plane.
Figure 2(b) displays the temperature dependence of Hall coefficient (RH). RH exhibits minimal temperature dependence above 260 K, but steeply decreases in absolute value below 260 K. Such a change in the RH suggests the reconstruction of Fermi surface at 260 K, which cannot be understood in the scheme of rigid band structure in doped n-type semiconductor. Similar behavior was also observed in the BaTiO3–δ with n = 1.6 × 1020 cm−3 10,12. The non-monotonic temperature dependence of charge transport implies the presence of structural phase transition into an unusual ferroelectric-like state, but the crystal structure in this enigmatic metallic system remains unexplored. In this study, to clarify the underlying interplay between conduction electrons and polarization, we have investigated the crystal structure and electron-lattice coupled dynamics in electron doped BaTiO3 by means of synchrotron x-ray scattering, electron diffraction and infrared optical spectroscopy.
We analyzed the crystal structure by means of single-crystalline synchrotron x-ray scattering and convergent-beam electron diffraction (CBED) on the electron-doped BaTiO3, (Ba0.97Sr0.03)0.98La0.02TiO3. The structural phase transition manifests itself as the splitting of fundamental Bragg reflections. Typical profiles of (400) reflections in the powder diffraction pattern are shown in Fig. 2(c). The peak splits below 350 K, indicating that the crystallographic symmetry is no longer cubic. We show the d-spacings of the (400)-reflections as a function of temperature in Fig. 2(d). The d-spacing of these two peaks suddenly bifurcates below 350 K. Moreover, the d-spacing of higher lying peak again exhibits a discontinuous change at 260 K, which nearly coincides with the cusp-like anomaly in temperature dependence of resistivity and Hall coefficient. These results indicate the presence of successive structural phase transitions at 350 K (=TS1) and 260 K (=TS2).
We further explored Bragg reflections in a wide reciprocal space region using the single-crystal x-ray oscillation photographs. Similar peak splitting is identified in other fundamental reflections, but no superlattice reflections are detected within the experimental accuracy. On the basis of collected reflections, the crystallographic symmetry between TS1 and TS2 is found to be tetragonal with the space group of either centrosymmetric P4/mmm or noncentrosymmetric P4mm. To distinguish these two candidates, we performed the CBED measurement, which can detect broken symmetries more sensitively than the ordinary x-ray diffraction owing to the dynamical diffraction effect13.
Figure 3(a) shows the zeroth-order Laue zone reflections of the CBED pattern taken at 290 K. The CBED pattern with the incident beam parallel to [001] axis exhibits the  symmetry, that is, a 4-fold rotation symmetry around [001] axis and two mirror symmetries respectively perpendicular to [100] and [110] directions. Conversely, as exemplified in Fig. 3(b), the CBED pattern with the incident beam parallel to [100] axis does not exhibit a mirror symmetry perpendicular to [001] axis, while a mirror symmetry perpendicular to [010] axis is maintained. This is not consistent with the centrosymmetric P4/mmm symmetry, but rather agrees with the noncentrosymmetric P4mm structure, which is compatible with the presence of polar axis (electric polarization) along [001] direction. Given the polar crystallographic symmetry, we refined the single crystalline synchrotron x-ray diffractogram and analyzed the crystal structure with reliability factors R = 2.10% and Rwp = 2.49% (Supplemental Information 1). The detail of structural parameters are listed in Table 1.
symmetry, that is, a 4-fold rotation symmetry around [001] axis and two mirror symmetries respectively perpendicular to [100] and [110] directions. Conversely, as exemplified in Fig. 3(b), the CBED pattern with the incident beam parallel to [100] axis does not exhibit a mirror symmetry perpendicular to [001] axis, while a mirror symmetry perpendicular to [010] axis is maintained. This is not consistent with the centrosymmetric P4/mmm symmetry, but rather agrees with the noncentrosymmetric P4mm structure, which is compatible with the presence of polar axis (electric polarization) along [001] direction. Given the polar crystallographic symmetry, we refined the single crystalline synchrotron x-ray diffractogram and analyzed the crystal structure with reliability factors R = 2.10% and Rwp = 2.49% (Supplemental Information 1). The detail of structural parameters are listed in Table 1.
The patterns of convergent beam electron diffraction for the incident beams.
(a) along [001] and (b) [100] axes at 290 K (tetragonal phase). The symmetries are 4mm and m, respectively. X-ray oscillation photographs around (009) reflection at (c) 270 K and (d) 20 K. The red dotted and black dashed lines denote the [001],  and
and  axis, respectively. The color-scale bar at right side of figure denotes the diffraction intensity in arbitrary units.
axis, respectively. The color-scale bar at right side of figure denotes the diffraction intensity in arbitrary units.
At temperatures below TS2, characteristic diffuse scattering emerges near fundamental reflections, in addition to the aforementioned peak splitting. Figure 3(d) exemplifies an x-ray oscillation image around the fundamental Bragg reflection at (009). One can see butterfly-shaped diffuse scattering extending along  direction, in contrast with the Bragg reflection in tetragonal phase as shown in Fig. 3(c). The spatial correlation length estimated from both the width of diffuse scattering and the dark-field transmission electron microscope image is of the order of 10 nm (Supplementary Information 2). This suggests that the polar structure is heterogeneous on nanometer scale and the macroscopic polar axis points to a certain direction in-between
direction, in contrast with the Bragg reflection in tetragonal phase as shown in Fig. 3(c). The spatial correlation length estimated from both the width of diffuse scattering and the dark-field transmission electron microscope image is of the order of 10 nm (Supplementary Information 2). This suggests that the polar structure is heterogeneous on nanometer scale and the macroscopic polar axis points to a certain direction in-between  and
and  axis within
axis within  plane as schematically shown in Fig. 1. We note that such a nanometer-scale heterogeneous polar structure with characteristic butterfly-shaped diffuse scattering has not been identified in pure BaTiO3, but is rather a common feature of the polar embryo structure in “frustrated”/relaxor ferroelectrics with giant permittivity and piezoelectric response14,15,16. Specifically, at the morphotropic phase boundary in canonical piezoelectrics Pr(Zr1–xTix)O3, the tetragonal phase thermally turns into the frustrated ferroelectric phase with polar embryo structure at lower temperatures, similar to the series of structural transformations in the present system. This low-temperature polar structure appears to be of monoclinic symmetry in a macroscopic scale, but is complex in a microscopic scale. So far, a variety of scenarios including the nanometer scale coexistence of tetragonal-, rhombohedral- and monoclinic-domains have been proposed as plausible microscopic models, but their relevance is still under intensive debate16,17,18,19,20,21,22. Regardless of specific models, it is commonly recognized that the “directional frustration” of electric polarization (P) driven by the critical competition between the rhombohedral phase (
plane as schematically shown in Fig. 1. We note that such a nanometer-scale heterogeneous polar structure with characteristic butterfly-shaped diffuse scattering has not been identified in pure BaTiO3, but is rather a common feature of the polar embryo structure in “frustrated”/relaxor ferroelectrics with giant permittivity and piezoelectric response14,15,16. Specifically, at the morphotropic phase boundary in canonical piezoelectrics Pr(Zr1–xTix)O3, the tetragonal phase thermally turns into the frustrated ferroelectric phase with polar embryo structure at lower temperatures, similar to the series of structural transformations in the present system. This low-temperature polar structure appears to be of monoclinic symmetry in a macroscopic scale, but is complex in a microscopic scale. So far, a variety of scenarios including the nanometer scale coexistence of tetragonal-, rhombohedral- and monoclinic-domains have been proposed as plausible microscopic models, but their relevance is still under intensive debate16,17,18,19,20,21,22. Regardless of specific models, it is commonly recognized that the “directional frustration” of electric polarization (P) driven by the critical competition between the rhombohedral phase ( ) and tetragonal phase (
) and tetragonal phase ( ) significantly reduces the uniaxial anisotropy, leading to the nanoscale complex domain structures. Since pure BaTiO3 and its lightly doped analog with highly insulating state rarely exhibit such a frustrated ferroelectric phase, aside from the metastable state under the intense electric field23, it is clear that the introduced conduction electrons play a crucial role in the unique structural phase transitions of the present system. Henceforth, we term this frustrated ferroelectric phase below TS2 the ‘monoclinic’ phase.
) significantly reduces the uniaxial anisotropy, leading to the nanoscale complex domain structures. Since pure BaTiO3 and its lightly doped analog with highly insulating state rarely exhibit such a frustrated ferroelectric phase, aside from the metastable state under the intense electric field23, it is clear that the introduced conduction electrons play a crucial role in the unique structural phase transitions of the present system. Henceforth, we term this frustrated ferroelectric phase below TS2 the ‘monoclinic’ phase.
To clarify the entanglement between conduction electrons and electric polarization, we have investigated the charge-lattice coupled dynamics using the infrared spectroscopy. Figure 4(a) is a magnified view of the optical conductivity spectra below 0.04 eV in the paraelectric phase. Two broad peaks and one sharp peak are identified around 7, 15 and 23 meV, respectively. Referring to the infrared phonon modes for BaTiO324,25, the sharp peak at 23 meV is assigned to the phonon governed by the Ba motion (Last mode), while the broad peaks around 7 and 15 meV can be the polarization relaxation mode (central mode) or Slater mode (soft phonon). Figure 4(b) shows the temperature dependence of optical conductivity spectra. The spectral intensity is significantly enhanced as temperature decreases, while the typical energy scale of the peaks barely changes. Below 100 K, the two peaks combine into, nearly, a single peak. Henceforth, we do not distinguish these two modes and regard them as a soft phonon. In order to quantify the temperature dependence of its spectral intensity, we fitted the spectra with the model of a damped harmonic oscillator coupled to a Debye mode (Supplement Information 3). Figure 4(c) shows the temperature evolution of spectral intensity for the soft phonon. The spectral intensity monotonically increases with decreasing temperature in the whole temperature range. Specifically, it is steeply enhanced below TS2 and nearly doubles at the lowest temperature. Moreover, the width of soft mode remains as large as 20 meV even at 10 K. The overdamped character and temperature-insensitive energy of the soft phonon well below the transition temperature as well as its enhanced spectral intensity are rarely observed in conventional ferroelectrics. Indeed, in pristine BaTiO3, the soft phonon usually exhibits a hardening below the ferroelectric transition temperature while reducing its overdamped character in accord with the growth of ferroelectric order26,27. This suggests that the delocalized conduction electrons play an important role in the polarization dynamics.
(a) Optical conductivity spectra at 360 K. The closed triangle, open triangle and closed square mark the polarization relaxation mode, Slater mode and Last mode, respectively. The thin blue, green and dashed lines denote the contribution from the Drude response, the damped harmonic oscillators coupled to Debye mode and fitted spectra, respectively. (b) The optical conductivity spectra at various temperatures. The closed (open) circles mark the dc-conductivity at 10 K (360 K) deduced from the resistivity measurements. (c) Temperature evolution of the spectral intensity of soft phonon band. (d) The loss function Im[1/ε] spectra at 360 K. The diamond denotes the energy of longitudinal optical (LO) phonon.
This scenario is further supported by the nonresonant inelastic x-ray scattering (IXS) spectra. Figure 5(a) displays the IXS spectra at various reduced wave vectors (q) along (110) in the paraelectric phase taken at 350 K. Here, phonons with polarization parallel to [001] direction, that is, the transverse phonon is discernible due to the nearly orthogonal relation between the polarization vector and q. The IXS spectrum at q = 0.08 shows two intense peaks at 5 and 23 meV due to the transverse acoustic (TA) phonon and Last mode, respectively. Moreover, the soft mode manifests itself as a broad continuum with significantly reduced scattering intensity around 10 meV. The mode around 28 meV with broad peak width may be attributed to the multiphonon band or infrared inactive optical phonon. We note that a similar intensity profiles of phonons are observed in the perovskite-type ferroelectrics Sr1–xBaxMnO328, supporting our mode assignment. To derive the energy of each mode, we assumed the damped harmonic oscillators to reproduce spectra. The energy dispersion of each mode is summarized in Fig. 5(b). The energy of soft mode appears to decrease with approaching Γ-point as often seen in various perovskite-type ferroelectrics. Figure 5(c) displays the temperature dependence of IXS spectra at (0.08 0.08 5). The IXS intensity exhibits minimal temperature dependence around 10 meV, in contrast with the large temperature dependence of infrared spectra. In general, the scattering intensity of nonresonant IXS is governed by that of phonons, while the intensity of infrared spectra is sensitive to both electronic excitations and infrared active optical phonons29,30,31. Therefore, the enhanced infrared intensity of soft phonon suggests the presence of electronic excitation, which is strongly coupled to the soft phonon.
(a) Inelastic x-ray scattering spectra taken at 350 K. The blue, red and green lines denote the fitted results for transverse acoustic mode, soft mode and Last mode, respectively. The mode around 28 meV denoted by purple lines may be multi-phonon band or infrared inactive optical phonon. (b) Energy dispersion of phonons. The energies at q = 0 (open symbols) are determined by the optical conductivity spectra. (c) The inelastic scattering spectra at various temperatures at Q = (0.08 0.08 5). The peak-like structure below 3 meV is an artifact due to the Bose correction.
One may think of the possibility of a multiphonon side band of conduction electrons (Drude) response, stemming from the underlying longitudinal phonon mode. However, this is not likely, since the longitudinal mode with the lowest energy is located around 22 meV, as inferred from the spectra of loss function shown in Fig. 4(d). A more plausible scenario is the direct interaction between the doped electrons and soft phonon. It is well known that the interaction between the infrared active optical phonon (transverse optical mode) and underlying electronic excitation manifests itself as an enhancement of infrared spectral intensity or asymmetric spectral shape in a variety of materials including charge transfer complex, graphene and transition metal oxides29,30,31. In the present system, the underlying electronic excitation around 20 meV is nothing but Drude response. Thus, the significant enhancement of spectral intensity for soft phonon can be attributed to the interaction with the Drude response, more specifically, the coupling between the polarization and conduction electrons. Incidentally, the spectral weight of soft phonon coupled to the Drude response may be related to that of the polaronic optical excitation appearing as the dopant induced in-gap state in the mid-infrared region (data not shown). The enhanced intensity of the former should be compensated by the reduction of the latter at low temperatures, while this sum rule cannot be clearly identified within our experimental accuracy. Although the direct interaction between conduction electrons and infrared active transverse phonon is usually negligible in centrosymmetric metals or semiconductors, it can be promoted by the broken inversion symmetry as in the present case. Indeed, within the scheme of quantum kinetic theory, Edelstein proposed that the transverse mode can mix with the longitudinal one in a medium with polar symmetry, that is, the fluctuation of the electric dipole of the transverse optical phonon can interact with the local fluctuation of conduction electron density via the electrostatic (Fröhlich) interaction32. Such an unusual coupling between the electric polarization and conduction electrons inherent to the polar crystallographic symmetry may be responsible for realizing the emergent ferroelectric structure compatible with metallic charge transport in this most canonical ferroelectrics.
To summarize, we demonstrated that an emergent polar metallic phase characterized by the nanometer-scale complex domain structure is invoked by doping the canonical ferroelectric BaTiO3 with conduction electrons. In this phase, the uniaxial anisotropy of polarization appears to be significantly reduced due to the competing ferroelectric phases with different polarization directions, reminiscent of the polar embryo structure in frustrated/relaxor ferroelectrics. Moreover, the spectral intensity of infrared soft phonon is remarkably enhanced in this metallic phase, suggesting the presence of unusual coupled dynamics between polarization and conduction electrons promoted by the broken inversion symmetry. The doped ferroelectrics may offer a fertile ground for research of the unique entanglement between the static/dynamic ferroelectric structure and charge transport phenomena via unusual electron-lattice coupling.
Methods
Crystal growth and transport measurements
The single crystalline samples of (Ba0.97Sr0.03)0.98La0.02TiO3 were grown by the floating zone method in Ar-atmosphere. Here, Sr is dilutely doped for a technical reason; a large-size single crystal can be acquired by avoiding the incorporation of hexagonal (non-perovskite) crystal structural phase during the crystal growth. The electrical or structural properties of the dilutely Sr-doped system is similar to those of Sr-free system. The quality of crystal was structurally characterized by the in-house x-ray diffraction. The resistivity and Hall resistivity was measured with use of the four-probe method using a commercial instrument (Physical Property Measuremet System, Quantum Design).
X-ray scattering
The x-ray diffraction experiment was performed using imaging plate diffractometers and Si(111) monochromatized synchrotron radiation 35 keV and 24.7 keV at the beam lines 02B1 and 44B2 at SPring-8, respectively. The size of ferroelectric clusters is defined as ξ = FWHM−1, where FWHM (nm−1) denotes the full-width at half-maximum of the Lorentzian fit to the data. The spectra of inelastic x-ray scattering were acquired at beam line 43LXU at SPring-8. The data were collected using the Si (11 11 11) reflection at 21.748 keV. The typical momentum and energy resolution, ΔQ is (0.03 0.03 0.04) in reciprocal lattice unit and 1.8 meV, respectively.
Transmission Electron Microscopy
The foil specimens for transmission electron microscopy (TEM) experiments were prepared by crushing the single crystal and mounting the fragments onto Cu grids. Convergent-beam electron diffraction patterns were obtained using an energy-filter TEM (JEM-2010FEF) at an accelerating voltage of 100 kV. Dark-feld TEM images were obtained using a conventional TEM (JEM-2100F) at an accelerating voltage of 200 kV. A liquid-nitrogen cooling holder was used to control temperature of specimens.
Optical measurements
Temperature dependence of reflectivity spectra at nearly normal incidence was measured between room temperature and 10 K in the energy region of 5 meV–5 eV with polarized light. We used a Fourier transform spectrometer (grating-type monochromator equipped with a microscope) in the photon energy region of 0.008–0.7 eV (0.5–5 eV). In the region of 3–40 eV, we carried out the measurement at room temperature with use of synchrotron radiation at UV-SOR, Institute for Molecular Science, Japan. The optical conductivity spectra were derived on the basis of Kramers-Kronig analysis. The Hagen-Rubens extrapolation were assumed below 5 meV and ω−4-type extrapolation above 40 eV.
Additional Information
How to cite this article: Fujioka, J. et al. Ferroelectric-like metallic state in electron doped BaTiO3. Sci. Rep. 5, 13207; doi: 10.1038/srep13207 (2015).
References
Spaldin, N. A. & Fiebig, M. The Renaissance of Magnetoelectric Multiferroics. Science 309, 391 (2005).
Cheong, S.-W. & Mostovoy, M. Multiferroics: A magnetic twist for ferroelectricity. Nature Mater. 6, 13–20 (2007).
Scott, J. F. Applications of Modern Ferroelectrics. Science 315, 954–959 (2007).
Kimura, T. et al. Magnetic control of ferroelectic polarization. Nature 426, 55 (2003).
Katsura, H., Balatsky, A. V. & Nagaosa, N. Spin current and magnetoelectric effect in noncollinear magnets. Phys. Rev. Lett. 95, 057205 (2005).
Pimenov, A. et al. Possible evidence for electromagnons in multiferroic manganites. Nature Phys. 2, 97 (2006).
Takahashi, Y. et al. Magnetoelectric resonance with electromagnons in a perovskite helimagnet. Nature Phys. 8, 121–125 (2011).
Tokura, Y., Seki, S. & Nagaosa, N. Multiferroics of spin origin. Rep. Prog. Phys. 77, 076501 (2014).
Fritsch, V. et al. Metal-to-insulator transition in La1–xBaxTiO3 . Phys. Rev. B. 64, 045113 (2001).
Hwang, J. et al. Doping and temperature-dependent optical properties of oxygen-reduced BaTiO3–δ. Phys. Rev. B 82, 214109 (2010).
Jeong, I.-K. et al. Structural evolution across the insulator-metal transition in oxygen-deficient BaTiO3–δ studied using neutron total scattering and Rietveld analysis. Phys. Rev. B 84, 064125 (2011).
Kolodiazhnyi, T., Tachibana, M., Kawaji, H., Hwang, J. & Takayama-Muromachi, E. Persistence of Ferroelectricity in BaTiO3 through the Insulator-Metal Transition. Phys. Rev. Lett. 104, 147602 (2010).
Tanaka, M. & Tsuda, K. Convergent-beam electron diffraction. J. Electron Microsc. 60, S245–S267 (2011).
You, H. & Zhang, Q. M. Diffuse X-Ray Scattering Study of Lead Magnesium Niobate Single Crystals Phys. Rev. Lett. 79, 3950 (1997).
Xu, G., Shirane, G., Copley, J. R. D. & Gehring, P. M. Neutron elastic diffuse scattering study of Pb(Mg1/3Nb2/3)O3 . Phys. Rev. B. 69, 064112 (2004).
Burkovsky, R. G. et al. Structural Heterogeneity and Diffuse Scattering in Morphotropic Lead Zirconate-Titanate Single Crystals. Phys. Rev. Lett. 109, 097603 (2012).
Noheda, B. et al. A monoclinic ferroelectric phase in the Pb(Zr1–xTix)O3 solid solution Appl. Phys. Lett. 74, 2059 (1999).
Vanderbilt, D. & Cohen, M. H. Monoclinic and triclinic phases in higher-order Devonshire theory. Phys. Rev. B. 63, 094108 (2001).
Woodward, D. I., Knodsen, J. & Reaney, I. M. Review of crystal and domain structures in the PbZr1–xTixO3 solid solution. Phys. Rev. B. 72, 104110 (2005).
Schierholz, R. et al. Crystal symmetry in single domains of PbZr0.54Ti0.46O3 . Phys. Rev. B. 78, 024118 (2008).
Phelan, D. et al. Single Crystal Study of Competing Rhombohedral and Monoclinic Order in Lead Zirconate Titanate. Phys. Rev. Lett. 105, 207601 (2010).
Gorfman, S. et al. High-resolution x-ray diffraction study of single crystals of lead zirconate titanate. Phys. Rev. B. 84, 020102(R) (2011).
Cao, H. et al. Monoclinic MC phase in (001) field cooled BaTiO3 single crystals Appl. Phys. Lett. 94, 032901 (2009).
Hlinka, J. Coexistence of the Phonon and Relaxation Soft Modes in the Terahertz Dielectric Response of Tetragonal BaTiO3 . Phys. Rev. Lett. 101, 167402 (2008).
Ponomareva, I., Bellaiche, L., Ostapchuk, T., Hlinka, J. & Petzelt, J. Terahertz dielectric response of cubic BaTiO3 . Phys. Rev. Lett. 77, 012102 (2008).
Ostapchuk, T., Petzelt, J., Savinov, M., Buscaglia, V. & Mitoseriu, L. Grain-size effect in BaTiO3 ceramics: study by far infrared spectroscopy Phase Transitions, 79, 361–373 (2006).
Petzelt, J. et al. Broadband Dielectric Spectroscopy of Ba(Zr,Ti)O3: Dynamics of Relaxors and Diffuse Ferroelectrics Ferroelectrics, 469, 14–25 (2014).
Sakai, H. et al. Soft phonon mode coupled with antiferromagnetic order in incipient-ferroelectric Mott insulators Sr1–xBaxMnO3 . Phys. Rev. B. 86, 104407 (2012).
Rice, M. J., Lipari, N. O. & Strassler, S. Dimerized Organic Linear-Chain Conductors and the Unambiguous Experimental Determination of Electron-Molecular-Vibration Coupling Constants. Phys. Rev. Lett. 39, 1359 (1977).
Kuzmenko, A. B. et al. Gate Tunable Infrared Phonon Anomalies in Bilayer Graphene. Phys. Rev. Lett. 103, 116804 (2009).
Proper, D. et al. Fano Resonances in the Infrared Spectra of Phonons in Hyperkagome Na3Ir3O8 . Phys. Rev. Lett. 112, 087401 (2014).
Edelstein, V. M. Features of light reflection off metals with destroyed mirror symmetry. Phys. Rev. B. 83, 113109 (2011).
Acknowledgements
Authors thank Y.Taguchi, J.G.Checkelsky, H.Sakai, S.Ishiwata and K.Sugimoto for enlightening discussions. This work was partly supported by Grant-In-Aid for Science Research (Nos. 24224009, 26610097) from the MEXT, Japan and by Funding Program for World-Leading Innovation R&D on Science and Technology (FIRST) on “Quantum Science on Strong-Correlation”. The synchrotron x-ray diffraction experiments were performed at BL44B2 in SPring-8 with approval of RIKEN (Proposed Nos. 20110099 and 20120085) and BL02B1 (Proposed No. 2012A1009).
Author information
Authors and Affiliations
Contributions
J.F., A.D. and K.O. carried out the measurements of charge transport property and optical spectra. Y.K. fabricates the single crystalline samples. D.O., D.M., T.A., K.K. and M.T. performed the x-ray diffraction and electron beam diffraction experiments. J.F., T.F., H.U., D.I. and A.B. performed the inelastic x-ray scattering experiments. J.F. analyzed the data and wrote the manuscript with contributions from all authors. T.A. and Y.T. contributed to discussion of the results and guided the project. Y.T. conceived and coordinated the project.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Fujioka, J., Doi, A., Okuyama, D. et al. Ferroelectric-like metallic state in electron doped BaTiO3. Sci Rep 5, 13207 (2015). https://doi.org/10.1038/srep13207
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep13207
This article is cited by
-
Nonzero spontaneous electric polarization in metals: novel predictive methods and applications
Scientific Reports (2024)
-
Quantum fluctuation of ferroelectric order in polar metals
npj Quantum Materials (2023)
-
Terahertz lattice and charge dynamics in ferroelectric semiconductor SnxPb1−xTe
npj Quantum Materials (2022)
-
Interface-induced magnetic polar metal phase in complex oxides
Nature Communications (2019)
-
Electron engineering of metallic multiferroic polarons in epitaxial BaTiO3
npj Computational Materials (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.