Introduction

Carbon has a large number of allotropes, including graphite, graphene, diamond, fullerenes and carbon nanotubes (CNTs) under the ambient pressure, because it is able to form sp-, sp2- and sp3-hybridized bonds. New functional carbon allotropes have been the focus of numerous theoretical and experimental explorations, because of not only their importance in basic science but also broad application prospects in technology.

In the past decades, the high pressure behaviors of carbon have a ttracted the attention of scientists. Compressing different carbon allotropes, such as graphite, fullerenes and CNTs, can product various phases, such as diamond, superhard post-graphite phases1,2,3,4,5,6, unprecedented hard nanotwinned diamond7, fullerene polymers8, amorphous carbon9 and some elusive allotropes10,11,12. Meanwhile, some theoretical tools for predicting the structures and the kinetic process are necessary and have yielded great success, such as genetic algorithm13, basin hopping14,15, evolutionary metadynamics16, variable-cell nudged elastic band method17,18 and transition path sampling method19.

CNTs are a kind of specific one-dimensional carbon materials with outstanding mechanical and electronic characters. Since the band structures of CNTs can be considered as band-folding of graphene20, armchair (n, n) tube is metallic with one-dimensional Dirac fermions as the projection of graphene band structure. The high pressure behaviors of the CNT systems have attracted much experimental21 and theoretical22 interest, due to the complex and interesting phase transitions under high pressure. Pressure makes the tubes close to each other and then the nearest neighbor carbon atoms among the adjacent tubes transit from sp2 to sp3 states and bond inter-cube. These novel metastable phases can be called as the single-walled CNT (SWCNT) polymers22. However, the polymer models did not consider the fact that the carbon atoms with sp2 and sp3 hybridization favors to possess different configurations, such as planar trigons and tetrahedrons. This will force to reconstruct the structures and then to happen more complex phase transition.

Results

Structure

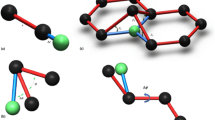
We use tetragonal stacking (6, 6)-CNTs as the precursors to perform the relaxation under different pressures and then to obtain the new carbon allotropes. When the pressure is changed from 40 to 60 GPa, the transition will fall into a trap of new phase, as the procedure shown in Fig. 1. Initially, the tubes approach to each other and there appear new connecting among the tubes as former paper22 presented (Fig. 1a,c). Firstly the compression makes the original cylinder tubes (Fig. 1a) to become into the rounded squares (Fig. 1b). Then the newly formed sp3 carbon atoms (cyan) force the neighboring atoms (red) away from each other and the four edges of the rounded square become concaved (Fig. 1c). Meanwhile, the sp2 atoms favor to stay in a plane, which further exacerbates the concavity of the tubes (Fig. 1d). And then the tubes transform to pinwheel shapes (Fig. 1e). Finally, some bonds are broken and some new bonds are rebuilt, resulting in the formation of a new phase (Fig. 1f). Such a new structure can be considered as the second step product of the CNT compression with sp2 and sp3 hybridization reconfiguring the geometry, while the SWCNT polymers can be the first order product. Surprisingly, we also decompress to the atmospheric pressure and find that it has low energy, good mechanic characters and fantastic band structure, as the following discussion.

Figure 1
figure 1

Formation process of bct-C12 from compression of (6, 6)-CNT at 40 GPa.

Cyan atoms indicate the atoms connecting independent tubes in the compression procedure. Red atoms indicate the atoms which have new bonding in the procedure and yellow bonds show the broken bonds in d and e.

Full size image

This new phase is identified to exhibit the body-centered tetragonal I4/mcm symmetry and is designated as the bct-C12, in which its conventional cell contains 24 atoms (Fig. 2) and its primitive cell has 12 atoms (Fig. 2b). At zero pressure, it has lattice parameters of a = b = 8.5 Å and c = 2.45 Å. Carbon atoms occupy the Wyckoff positions 8h (0.21, 0.29, 0) and 16k (0.73, 0.96, 0), respectively. In particular, the atoms located at the 8h Wyckoff positions have sp3 hybridization (painted in grey in Fig. 2e) and those occupying the 16k have sp2 hybridization (painted in yellow in Fig. 2e). Due to the same D4h point group, the bct-C12 has much structural similarity to bct-C4 (refs. 5,6). It can be found that if we use zigzag carbon chains to replace the 4-ring of the bct-C4, the bct-C4 (Fig. 2d) becomes into the bct-C12 (Fig. 2d) in geometric configuration. However, the atoms in the additional zigzag chain are sp2 hybridization, while the atoms in the original bct-C4 are sp3 hybridization.

Figure 2
figure 2

Geometric structure of bct-C12.

a, c the conventional cell of bct-C12 from (0,0,1) direction and (1, 0, 0) direction. b the primitive cell of bct-C12. d, e the relationship between the structures of bct-C4 and bct-C12.

Full size image

Stability

The bct-C12, as a metastable phase of carbon at atmospheric pressure, has a formation energy of 0.18 eV/atom relative to graphite, while the bct-C4 is 0.26 eV/atom, the M-carbon 0.17 eV/atom, the (6,6)-CNT 0.13 eV/atom and the fullerene C60 0.39 eV/atom, respectively. One should be emphasized that the above results we calculated are similar to the previous calculations3,5,6,23. This means that the bct-C12 has the similar stability to the precursor (6, 6)-CNT and the superhard post-graphite phases, M-carbon and the lower formation energy than bct-C4 and C60. In addition, the calculated phonon spectrum clearly indicates its dynamical stability (Fig. 3). Clearly, this phase is a novel material, even though the pressure is decompressed to the atmospheric pressure.

Figure 3
figure 3

Phonon spectrum of bct-C12 at zero pressure.

Full size image

Mechanical property

As shown in the calculation results, the bct-C12 has its bulk modulus of 315.9 GPa and shear modulus of 225.4 GPa. Based on the modified microscope model24,25,26, the calculated theoretical Vickers hardness is 31.6 GPa for the bct-C12. Although this hardness is much lower than 93.6 GPa of diamond, the bct-C12 is still a hard material with its Vickers hardness being slightly higher than 30.2 GPa of α-SiO2. In particular, the metallic property will dramatically reduce the hardness of material26, hence this hardness of the metallic bct-C12 should be quite high among the metallic materials. In addition, the bct-C12 has much interspace and its sp3 parts are not in a perfect tetrahedron. As a result, the structure is easy to slip. This is the reason why the bulk modulus of this structure is about 1.5 times of the shear modulus, which implies that this structure has better malleability than the superhard materials, such as diamond.

Electronic property

The band structure (Fig. 4a) indicates the bct-C12 to be metallic. Since the σ bands of the sp3 atoms have the lower energy, the bands cross the Fermi level are the π bands around the sp2 zigzag chain (red lines in Fig. 4a). In particular, the band structure has a novel property that, along the kz axis, the linear valence and conduction bands meet at a single point, which is similar to the Dirac point in graphene. These points of intersection depend on both kx and ky and show the energy fluctuation in Brillouin zone. The maximum and minimum of the points of intersection are 0.57 eV at FA (0, 0, 0.172) × 2πÅ−1 along the G-A line and −0.71 eV at FB (0.117, 0, 0.174) × 2π Å−1 along the Z-B line, respectively. It should be noted that since FA and FB have nearly the same z coordinates, the surface composed of these Dirac points is close to a plane, which can be referred to as the Dirac surface.

Figure 4
figure 4

Electric structure of bct-C12.

a the band structure of bct-C12. b the k path and Brillouin zone of bct-C12. c, the energy of the valence and conduction bands as a function of kx-kz plane. The maximum and minimum in Dirac surface in energy, FA and FB, are pointed out. FF shows the intersection of Fermi surface and Dirac surface. Zero point of energy is Fermi level. The units of kx and kz are 2π Å−1.

Full size image

We find a “weird” quasiparticle that exhibits a linear Dirac fermion behavior in the kz direction, while a classic two-order dispersion in the kx-ky plane, meaning that the quasiparticle can be changed from the Dirac fermions to the normal fermions by gradually changing the wavevector. As shown in Fig. 4c, in the kx-kz plane, the band exhibits an anisotropic wedge instead of the cone in graphene.

In particular, at the FA point, which is the top of this band, the slopes in the kz direction is ±39.1 eV.Å, equivalent to a velocity m/s, which is slightly bigger than that approaching the Dirac points of graphene, 34 eV.Å (v = 0.82 × 106 m/s). At this points, we have vx = vy = 0. The second derivatives in the kx and ky directions are −775.2 eV.Å2 for the valence band and −407.2 eV.Å2 for the conductive band, which indicate the effective mass of electron and , correspondingly the effective mass is −0.39me for the valence band and −0.74me for the conductive band, where me is the true electron mass. By contrast, the effective mass in the z direction is mzz = 0.

Meanwhile, the band bottom, FB point, is also close to the boundary of Brillouin zone, which distorts its Dirac behavior in the z direction. The slopes are −51.4 and 37.1 eV∙Å, correspondingly the velocity vz = 0.90 × 106 m/s in the +kz direction and −1.24 × 106 m/s (more than 1.5 times of that in graphene) in the −kz direction, while vx = vy = 0. In the kx-ky plane, the curvatures of the valance and conductive bands are 308.0 and 707.0 eV.Å2, respectively and then the corresponding effective mass is mxx = myy = 0.98me for the valence band and mxx = myy = 0.43me for the conductive band, while mzz = 0.

Since the Dirac surface crosses the Fermi surface (E = 0), which is of great importance to electronic transport, we also analyze the band property of their intersections, for instance in FF (0.054, 0, 0.170) × 2π Å−1. In the kz direction, the slopes are −59.4 and 30.7 eV∙Å, correspondingly the velocity vz = 0.74 × 106 m/s in the +kz direction and −1.43 × 106 m/s in the –kz direction, while mxx = 0. In the kx direction, FF is not an extreme point, so its slopes are nonzero. The slope of −15.4 eV∙Å corresponds to the velocity vx = 0.37 × 106 m/s in the −kx direction. The curvatures of the valance and conductive bands are −188.9 and 84.0 eV∙Å2 at FF, respectively, corresponding to the effective mass of mxx = myy = −1.59me for the valence band and mxx = myy = 3.58me for the conductive band. Because the band at FF is smoother than FA and FB, the quasi-particles are heavier.

By analyzing FA, FB and FF, we find the anisotropy of the massless Dirac behavior in the kz direction and the classic behavior in the kx and ky directions, is the intrinsic property of the Dirac surface in the Brillouin zone of bct-C12. It distributes in the energy space from −0.71 to 0.51 eV and is quite close to the Fermi level.

Discussions

The unexpected anisotropic Dirac fermion originates from the anisotropy of effective mass of the quasiparticle. True particles have spatial rotation invariance, so their masses are scalar constants. But three dimensional periodic system breaks the rotation invariance, so the effective mass of the quasiparticle in crystals is described by a 3 × 3 matrix tensor. In the general case, the three eigenvalues approach to each other and we can average them to give the averaged effective mass of the quasiparticle. By contrast, the bct-C12 is an extreme case. Especially, the bct-C12 inherits the zigzag carbon chain from its precursor (6, 6)-CNT, so it is massless Dirac fermion in the z direction. Unlike the normal CNT, however, the distance between the zigzag chains is only 3.02 Å which is close enough for the interaction between the 2p electrons around the sp2 C atoms beyond the tubes and the chain makes a common tetragonal lattice to have the classical band structure. As a result, it shows a strong anisotropy between the Dirac and classical behaviors.

Interestingly, although the bct-C12 is metallic, it should have the transport behavior like the semiconductor. Particularly, the FA point (0.57 eV) is slightly above the Fermi level, while the FB point (−0.71 eV) lies slightly below the Fermi level. So the Fermi level cross the Dirac surface (Fig. 4c) and the bct-C12 possesses the spontaneous electrons at FA and holes at FB in its ground state. Due to different signs of effective mass in the x-y plane, FA and FB are different doping and will obviously contribute differently to the electronic properties.

In conclusion, by compressing the (6, 6)-CNT, we discover a new tetragonal carbon phase, which can be quenchable when decompressing to zero pressure. It is metallic and as hard as α-quartz. Most strikingly, this structure has the anisotropy of the Dirac behavior in the kz direction and the classic behavior in the kx and ky directions, which originates from the interaction between the Dirac zigzag chains. To our knowledge, this should be the first reported a system that has anisotropy in both Dirac and classic fermions. This research provides a new member of the big family of carbon allotropes and novel insight to their transport behaviors. Of course, this new phase maybe have some unexpected electronic behaviors.

Methods

Carbon nanotubes packed in periodic crystal lattices with a standard intertube spacing of 3.4 Å were constructed using the Materials Studio package27. Structural relaxations and property calculations were performed based on the density functional theory (DFT) as implemented in the CASTEP code27. The Vanderbilt ultrasoft pseudopotential was used and the electron-electron exchange interaction was described by the local density approximation (LDA) exchange-correlation functional of Ceperley and Alder, as parameterized by Perdew and Zunger (CA-PZ)28,29. The plane-wave cutoff energy with 800 eV and a k-point spacing (2π × 0.03 Å−1) was used to generate Monkhorst-Pack k-points grids for Brillouin zone sampling30. Primitive cells were used to calculate the band structures and the bulk modulus and shear modulus. Vickers hardness is calculated using the modified microscopic model24,25,26. All the results were also confirmed by the all-electron projector augmented wave (PAW) method31 as implemented in the VASP code32. Phonon calculations were performed using the PHONOPY code33.

Additional Information

How to cite this article: Dong, X. et al. A new phase from compression of carbon nanotube with anisotropic Dirac fermions. Sci. Rep. 5, 10713; doi: 10.1038/srep10713 (2015).