Introduction

Fast electrochemical processes taking place on a complicated cytoarchitectural network structure render the human brain a highly complex dynamical system. Brain activity, as measured directly via EEG or MEG, or indirectly by means of MRI recordings, reveals characteristic macroscopic patterns such as oscillations in various frequency bands1, synchronization2,3,4, or chaotic dynamics5. Generally it is believed that macroscopic activity (involving neurons) is closely related to high-level functions such as cognition, attention, memory or task execution. To understand the mechanisms of this correspondence, both the overall network structure of the brain and the local properties of neural populations have to be taken into account4,6. Regarding the latter, neural inhibition seems to be essential for cortical processing7.

Two physiological phenomena received much attention lately in terms of a mathematical understanding: resting-state activity and gamma oscillations. Resting-state activity is spontaneous, highly structured activity of the brain during rest and can be described in terms of networks of simultaneously active brain regions8,9. Models of resting-state networks often rely on anatomical networks derived from histological or imaging data and on local interactions between populations of excitatory and inhibitory neurons10,11,12,13. Oscillatory neural activity in the gamma range ( Hz) is potentially related to consciousness and the binding problem although its precise function remains unclear14. To understand the origin of gamma oscillations, two mechanisms have been proposed15. One describes interactions between inhibitory neurons together with an external driving force16,17. The other mechanism is based on excitatory-inhibitory coupling with synaptic time delays18,19,20. The relation of gamma oscillations and inhibition is experimentally well established. In mice21, rats22 and humans3,23, a decrease of GABA-concentrations (gamma-aminobutyric acid is the main inhibitory neurotransmitter in mammals) is accompanied by a strong attenuation of the gamma frequency band and sometimes by epileptiform activity.

Many existing network models for resting-state activity and gamma oscillations are based on single-neuron local dynamics10,11,16,17,18,19. Since experimentally observed resting-state networks comprise individual regions containing about to individual neurons, we believe that a local description in terms of Wilson-Cowan equations is an attractive alternative. The subject of multiplex networks received recent attention with applications reaching from social and technological systems to economy and evolutionary games24,25.

In this work we derive a simple two-layer multiplex model from classical physiological equations that is able to capture the main features of cortical activity such as oscillations, synchronization and chaotic dynamics. This model unifies the roles of neural network topology, synaptic time delays and excitation/inhibition. It provides a closed framework for simultaneously understanding the origin of resting-state activity and gamma oscillations.

Results

Derivation of the multiplex Kuramoto model

We consider cortical regions indexed by , see Fig. 1a. Each region is populated by ensembles of excitatory and inhibitory neurons (e.g. pyramidal cells and interneurons). We define the activity level of a region as the fraction of firing excitatory (inhibitory) neurons of the total number of excitatory (inhibitory) neurons in that region at a unit time interval and denote it by (). Neglecting for the moment interactions between different regions, we assume that individual cortical regions obey the Wilson-Cowan-type dynamics20

where is a sigmoidal response function, and are real-valued feedback parameters and and are positive synaptic coefficients (). and account for external inputs, e.g. from sensory organs. We now introduce interactions among regions of the network by replacing in Eq. (1) by

Here , , , are positive synaptic coefficients linking regions and . accounts for transmission delays at inhibitory synapses (not to be confused with axonal conduction delays). In physiology, can be altered by changing the synaptic concentration of GABA18,19,21,22. In the present model, we assume that is proportional to the average synaptic GABA concentration in the brain. To derive a multiplex Kuramoto model (MKM) from Eqs. (1) and (2), we make the following three assumptions:

Figure 1
figure 1

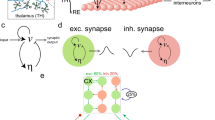
Schematic illustration of the model setup. a The cortical surface is divided into macroscopic regions. Every region (blue) comprises excitatory (green) and inhibitory (red) neural populations with activity levels and , respectively. Activity levels quantify the ratio of firing neurons in the region at time . b Region (left) receives excitatory (green arrows) and inhibitory (red arrows) inputs plus self-feedback (blue arrows). Inputs from adjacent regions (right) are weak (dashed arrows) or very weak (dotted arrow). c Variable transformation from activity variables and to phase deviation variables . On a limit cycle , -perturbations of the -dynamics at time induce the phase deviations .

Full size image

(i) Homogeneity. Cortical regions exhibit nearly identical dynamical behavior. We therefore assume the following parameters to be constant across regions,

for all , up to small perturbations, denoted by .

(ii) Stable local oscillations. We choose the parameters such that each uncoupled system Eq. (1), under the assumption given in Eq. (3), has a unique exponentially stable limit cycle . As a consequence, after a transient time solutions of Eq. (1) can be written as

where  (t) is an arbitrary solution of Eq. (1) on 26,27. accounts for specific initial values. Let denote the period of . We assume that the frequency lies in the physiological gamma range.

(iii) Weak coupling. Interactions between adjacent regions are weak and inhibitory-inhibitory interactions are very weak in the sense that,

for all . These assumptions are justified because the number of synaptic connections within a cortical region is much larger than between regions and excitatory neurons outnumber inhibitory neurons by approximately one order of magnitude28,29.

Figure 1b summarizes the connectivity structure between regions and . Region receives excitatory (green arrows) and inhibitory (red arrows) inputs plus feedback (blue arrows), magnitudes are indicated by the arrow labels. For the sake of clarity, arrows representing inputs of magnitude , and are drawn in continuous, dashed and dotted style, respectively.

Under these assumptions, the system Eq. (1) with Eq. (2) is equivalent (see SI) to a two-layer MKM

Here describes the deviations from the uncoupled phases that are associated with solutions of the uncoupled system Eq. (4). Accordingly, describes the deviations from the uncoupled oscillation frequency . Time has been rescaled, see SI. is the adjacency matrix of the excitatory-excitatory interaction network as defined in Eq. (5) and is a linear combination of the adjacency matrices and . accounts for the interaction between excitatory and inhibitory populations, see SI. and , are the corresponding average degrees. is a phase shift parameter related to the time delay via . is a global coupling constant that we assume to be proportional to the cerebral blood flow. This is reasonable because the latter is strongly correlated with the connection strengths of functional networks reconstructed in magnetic resonance imaging30. , the so-called natural frequencies of the MKM, are the constant contribution to the frequency deviations . We take from a symmetric, unimodal random distribution , with mean . Since the 1-parameter family of rotating-frame transformations , , leave Eq. (6) invariant for any , without loss of generality we assume, and . Note that for each solution with , there exists a solution with and . Physiological processes changing , and occur on a much slower timescale than neural activity.

It is known that weakly coupled, nearly identical limit-cycle oscillators can be described in terms of phase variables27,31,32,33. However, in terms of the new variables , interactions between cortical regions take place on two independent layers representing excitatory-excitatory and excitatory-inhibitory coupling, respectively and the complicated connectivity structure of Fig. 1b reduces to a simple two-layer multiplex structure. Figure 1c shows the variable transformation from activity variables and , to the phase variable for any cortical region. In the unperturbed case, , the limit cycle is parametrized by . Since is exponentially stable, -perturbations of activity dynamics lead to phase deviations . For we recover the Kuramoto model on a single network, see SI and34,35,36,37,38,39.

Order parameters

We characterize solutions of Eq. (6) by the following order parameters:

Synchronization

We define the order parameter32,33,34,40

It takes values between (no synchronization) and (full synchronization)27. Let denote its time average .

Chaotic dynamics

The instantaneous largest Lyapunov exponent is given by

where measures the separation between a reference trajectory and a perturbed one . is the initial separation at and is the -norm, see SI. For large times, approaches the “true” largest Lyapunov exponent, .

Average frequency deviation

We look at average frequency deviations across all regions,

once a stationary state is reached.

Numerical simulation of the model

Synchronization

We find that synchronization depends on the coupling strength and phase shift , Fig. 2a. For , we expect (see SI) a transition from an unsynchronized to a synchronized state at a critical value , which is confirmed by our simulations, Fig. 2a. With , stronger coupling is required for this transition to occur. Above a value of approximately , a global synchronized state ceases to exist.

Figure 2
figure 2

Dynamical properties of the multiplex Kuramoto model in terms of control- and order parameters as obtained by numerical simulation. a Order parameter and b largest Lyapunov exponent identify the mutually exclusive regions of synchronization and of chaotic dynamics in the -plane. The critical point ( indicates a phase transition of Kuramoto type in the case of vanishing synaptic time delays. The region is characterized by and . For , either and (synchronized region) or and (chaotic region). Within the chaotic region, the smallest values of are encountered at , where . The largest values of occur at the boundary with the synchronized region, with peak values of . c Schematic phase diagram inferred from a and b. Synchronized, unsynchronized and chaotic behavior can be clearly distinguished. Dashed arrows indicate directions along which distributions of frequency deviations were evaluated in Fig. 3d. Average frequency deviations in the -plane. Regions of frequency suppression, , have a large overlap with the synchronized phase.

Full size image

Chaotic dynamics

Above the synchronization threshold, , synchronization and chaotic dynamics are mutually exclusive, see Fig. 2b. For small values of , there exists a small chaotic region () at the Kuramoto transition, in agreement with the well-known results for , see SI. This region is expanding with increasing values of . At the boundary to the synchronized region, increasingly large values of are obtained. peaks at , for . In the unsynchronized region, , the dynamics is not chaotic, . For and , which constitutes the largest fraction of the chaotic region, the smallest values of Lyapunov exponents that we obtain are between and . Those values typically occur close to the border to the unsynchronized region, where is close to . For comparison, we note that at the classical Kuramoto transition ( and ), where chaotic behavior of the system is out of question35, values of maximally 0.07 are encountered in our model set-up. Figure 2c integrates both results (synchronization and chaotic dynamics) into a schematic phase diagram that clearly exhibits three phases.

Spectral properties

Figure 3a–c shows the stationary distributions of frequency deviations for selected values in the (,)-plane. For , the distributions are practically identical for different values of , Fig. 3a. For , at , a synchronization peak appears close to frequency zero. With increasing , this peak moves towards increasingly negative values, until . Between and , the distribution is rapidly becoming broader and shifts towards positive values. After reaching a maximum at , it is finally centered around zero again, Fig. 3b. , is similar, however larger positive and negative values for occur, Fig. 3c.

Figure 3
figure 3

Stationary distributions of frequency deviations for different values of (represented by different colors as indicated in the legend) and for a subcritical, b weakly and c strongly supercritical values of , respectively. according to Fig. 2. For supercritical , the simultaneous occurrence of rapid frequency suppression and narrowing of the distributions between and can be observed.

Full size image

Figure 2d shows the average frequency deviation as a function of and . As expected (see SI), we find frequency suppression associated with synchronization in the region of large and small , but also for large and intermediate . For fixed , maximal frequency suppression occurs at . For large and large (chaotic region) we find slightly positive .

Robustness issues

Homogeneity

The derivation of the MKM is based on three key assumptions, see Eqs. (3)–(5). If Eq. (3) is violated, i.e. the ensemble of uncoupled Wilson-Cowan oscillators is strongly heterogenous, several oscillation periods may occur . As a consequence, weak interactions become frequency-modulated27: Two oscillators interact only if their frequencies and are similar, in the sense that , where and are small numbers.

Uniqueness of local oscillations

Regarding Eq. (4), discarding the uniqueness of the limit cycles would result in heterogenous coupling strengths , or .

Stability of local oscillations and weak coupling

In contrast, both the exponential stability of the limit cycles and the weak coupling assumption, Eq. (5), are strictly necessary for the derivation of the MKM, since they allow for a dimensional reduction from activity- to phase deviation variables (see SI). If the dimensional reduction can not be carried through, the full system Eq. (1) with Eq. (2) has to be studied, whose properties are much harder to access.

Numerical simulation

We tested the model for robustness with respect to the particular choice of parameters. As suggested by various brain atlases and cortical parcellation schemes, a number of cortical regions seems reasonable41,42. We tested up to and found no deviations from the presented qualitative picture. For the link density , we find that as long as it exceeds the percolation threshold, , differences in simulations are marginal. Finally, we observe that like in the original Kuramoto model32,33, for different natural frequency distributions the qualitative behaviour remains practically unchanged as long as is unimodal and symmetric.

Discussion

In several variants of single-layer Kuramoto models with a phase shift or a time delay, frequency suppression appears37,39,43,44. In addition39, mentions chaotic behavior. However, the existence of the phase diagram with the three distinct macroscopic phases can not be inferred from any of those models to the best of our knowledge.

In Ref. 45, several modes of synchronization are reported for a Kuramoto model on two interconnected networks with an inter-network time delay. While this computational model does not exhibit chaotic or unsynchronized phases, it suggests that a more complicated network topology can lead to a deeper structure within the synchronized phase in Kuramoto-type models.

Since the present work emphasizes the derivation of the MKM and the study of its stationary properties, we did not investigate the details of the synchronization transition. In this context we mention that the emergence of synchronization follows different paths in different types of networks46. Further, if a correlation between natural frequencies and network properties is assumed, explosive synchronization and hysteretic effects may appear47.

Summarizing, we can show mathematically that a set of weakly coupled Wilson-Cowan oscillators on a cortical network with a synaptic time delay between excitatory and inhibitory neural populations is identical to a simple Kuramoto-type phase model on a two-layer multiplex network. Numerical investigations of this model reveal the presence of three distinct macroscopic phases in the space of control parameters (associated with cerebral blood flow) and (associated with synaptic GABA concentration). For couplings , activities of individual cortical regions show independent oscillatory behavior (unsynchronized). Frequencies are distributed symmetrically around an average frequency that we assume to be located in the physiological gamma range. This dynamical state corresponds to “background activity” of the brain. For , two phases are possible: for small , the system becomes synchronized, which corresponds to “epileptic seizure activity” in physiology. For large , synchronized activity only appears in clusters; the system is chaotic in general. We identify this phase with “resting-state activity” in the brain. An important property of the present model is that the average oscillation frequency is shifted towards lower values when crossing the boundary to the synchronized phase. This could explain the experimental fact2,21,22,23 that a decrease of the GABA concentration in the resting-state both triggers the appearance of epileptiform slow waves and diminishes gamma activity in the brain.

Methods

Equation (6) is integrated with a standard 4th-order Runge-Kutta algorithm with time steps of size . The system size is , both layers are chosen to be Erdös-Rényi networks with . Natural frequencies are taken from a standard normal distribution, initial phase deviations from the interval . The first time steps are discarded to exclude transient effects. For the remaining time steps, , and are evaluated. All results are averaged over identical, independent runs with different realizations of the initial conditions.

Additional Information

How to cite this article: Sadilek, M. and Thurner, S. Physiologically motivated multiplex Kuramoto model describes phase diagram of cortical activity. Sci. Rep. 5, 10015; doi: 10.1038/srep10015 (2015).