Abstract
Interspecific mutualisms consist of partners trading services that yield common benefits to both species. Until now, understanding how the payoffs from mutualistic cooperation are allocated among the participants has been problematic. Two hypotheses have been proposed to resolve this problem. The Red Queen effect argues that faster-evolving species are favoured in co-evolutionary processes because they are able to obtain a larger share of benefits. Conversely, the Red King effect argues that the slower-evolving species gains a larger share of benefits. The model we propose shows that the allocations for a common benefit vary when the effect of a reward mechanism is included in the model. The outcome is a shift from the Red Queen effect to the Red King effect and vice versa. In addition, our model shows that either an asymmetry in payoff or an asymmetry in the number of cooperative partners causes a shift between the Red Queen effect and the Red King effect. Even in situations where the evolutionary rates are equal between the two species, asymmetries in rewards and in participant number lead to an uneven allocation of benefits among the partners.
Similar content being viewed by others
Introduction
In mutualistic interactions between two species, both species benefit from cooperation. These interactions are ubiquitous in nature. Several well-studied theories have been proposed to explain the evolution and maintenance of mutualisms1,2,3,4,5. For example, the reciprocity selection theory views the beneficial exchange between species from a market perspective. This theory argues that the cooperative species gain a direct or an indirect benefit. Consequently, choosing a strategy of cooperation increases the fitness of both mutualistic species6,7. The kin selection theory explains that if, for example, symbiont virulence is transmitted vertically, then related symbionts increase their inclusive fitness by decreasing their total virulence, or even by cooperating with their host, due to the genes they share with other symbiotic individuals8,9. The authors of the sanction theory argue that hosts display sanctioning behaviours against exploiters or cheaters to maintain the stability of the mutualism10,11,12,13. Finally, the predator interference theory considers the case of predation within mutualistic interactions. Predation prevents the population increase of exploiters and favours the maintenance of the mutualism14,15.
The above theories have focused almost exclusively on how interspecific cooperation can persist over evolutionary time. They have also focused on why mutualistic interactions are conserved, as we would normally expect natural selection to favour exploiters. Cheaters disrupt the mutualistic stability when trying to gain excessive benefits and thereby decrease their contribution to the cooperative relationship16. However, although cooperation is maintained between two species by the mechanisms suggested above, how the resulting benefits are allocated to the cooperative species has not yet been extensively studied.
How mutualistic benefits are allocated between interacting species has puzzled empirical scientists for a long time. For example, in mutualistic interactions between a cleaner wrasse Labroides dimidiatus and its large client fish, the cleaner wrasse removes ectoparasites on the client fish, taking them as food and the client fish enjoys a reduced parasite load17,18. As reported by Bergstrom and Lachmann (2003), in an idealised interaction where there is no potential for cleaners to feed on live tissue or for clients to prey on cleaners19, the actual allocation of benefits between a cleaner wrasse and its client fish is relatively straightforward20. The allocation of benefits, however, is not as clear in other mutualisms, including ants and lycaenid butterfly caterpillars21, plant and pollinators22, or symbioses between insects and gut microbes23.
To date, two hypotheses have been proposed to address this issue. The Red Queen effect argues that the faster-evolving species should show an advantage in the co-evolutionary process. This effect describes the antagonistic co-evolution between two species over a common ecological resource, for example, between predator and prey or between host and parasite24. In 1999, Herre et al. noted that the Red Queen effect can also effectively describe mutualisms because these types of interactions are also an ongoing arms race4. By contrast, another school of thought argues that a slower rate of evolution should confer a more favourable outcome when two species compete for the benefits of a mutualism25,26,27. This effect has been called the Red King effect20. These two hypotheses are based on the assumption that the cooperative species do not produce any reward, even though such reward mechanisms have been widely observed28,29,30,31 (e.g., in the obligate interspecific cooperation between figs and fig wasps, the fig host can reward the cooperative pollinators indirectly by increasing the offspring development ratio32,33).
The theoretical models of the Red King and Red Queen hypotheses also assume that the distributions of payoffs between species are equal. However, almost all well-documented mutualisms–such as yucca plants and yucca moths34,35, legumes and nitrogen-fixing bacteria10 and figs and fig wasps33–have shown that the hosts and symbionts have highly asymmetric payoffs. In principle, the host can therefore always set the rules of the game between mutualistic species. Consistent with this principle, hosts of different mutualisms were recently shown to discriminatively sanction non-cooperative actors and reward cooperative actors to maintain the mutualistic interaction10,13. Another more extreme phenomenon is when the host completely represses the population of symbionts36. Thus, we argue that the reward mechanism and other asymmetric factors (e.g., asymmetric payoffs and asymmetry in the number of players) play a fundamental role in the evolution of mutualisms. In this study, by using a multiplayer game model, we explicitly considered the role of reward mechanisms and asymmetric factors in coevolved mutualisms and we analysed their effects on the allocation of mutualistic benefits.
Results
Model
In this model, we assume that individuals of species 1 and 2 are selected at random from the population and form groups of size d1 and d2, respectively. The members of the two species engage in pairwise or multiplayer repeated interactions. The interactions between the two species/groups are shown in Figure 1. At every turn, every individual needs to decide whether to cooperate or to defect. These interactions can thus be depicted by a two-population role-asymmetric game37,38. The relative payoff matrix is shown in Table 1. In this matrix, the row players belong to one of the species and the column players belong to the other species. For example, a cooperative individual of species 1 obtains a payoff of  when playing against a cooperative individual of species 2, whereas a cooperative individual of species 2 obtains a payoff of
when playing against a cooperative individual of species 2, whereas a cooperative individual of species 2 obtains a payoff of  . Here,
. Here,  for i, j = 1, 2 and i ≠ j. This rank order of payoffs corresponds to the snowdrift game. For a classical, single-species, pairwise snowdrift game, there exists a mixed evolutionary stable state at which the proportion of cooperative individuals is 1 − c/(2b − c). However, for a snowdrift game between two species, this coexistence point is unstable because each species would be better off defecting. Two equilibria arise in which neither player can do better by changing their strategies: one player from species 1 cooperates and the other from species 2 defects (or vice versa).
for i, j = 1, 2 and i ≠ j. This rank order of payoffs corresponds to the snowdrift game. For a classical, single-species, pairwise snowdrift game, there exists a mixed evolutionary stable state at which the proportion of cooperative individuals is 1 − c/(2b − c). However, for a snowdrift game between two species, this coexistence point is unstable because each species would be better off defecting. Two equilibria arise in which neither player can do better by changing their strategies: one player from species 1 cooperates and the other from species 2 defects (or vice versa).
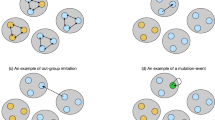
The interactions between species 1 and 2 in mutualisms.
We assume that d1 = 5, d2 = 6. Species 1 plays in a seven-player game. In this first game, we choose one player of species 1 (the blue faces) to interact with six players of species 2 (the red faces). Species 2 plays a six-player game. In this second game, one player of species 2 joins and interacts with all the players of species 1. Generally, for a d1 + 1 players' game for species 2, we choose one individual from species 2 to interact with d1 individuals of species 1. For a d2 + 1 players' game for species 1, we pick one individual from species 1 to interact with d2 individuals of species 2. We do not consider intraspecific interactions within groups. It is possible to incorporate even more complexity by considering these interactions within the same species. By doing this, however, the model becomes very convoluted and beyond the scope of this paper. Figure 1 was produced with Microsoft Word. Other figures were obtained with Maple 15.
The above approach can be extended to multiplayer games. In this case, the payoff we report below (Table 2) is often adopted (reported from Souza et al. 2009)39. Here, the cost c is shared between cooperative individuals. In addition, it is possible that a particular threshold needs to be met for the mutualistic benefits to materialise. For example, client fishes have been observed to choose cleaning stations with two cleaners over lone cleaners17. Similarly, in observations of the interactions between ants and caterpillars, a particular number of ants are required to rescue a caterpillar from its predator. It has also been shown that the quantity of secretions of a lycaenid larva is correlated to the number of attending ants40. Generalising from these examples, we assume that the number of cooperative individuals k is at least equal to M and that the benefit b is acquired in turn. For different species, the payoff setup has different values: bi, ci and Mi with 1 ≤ Mi ≤ di + 1 and bi > ci (i = 1,2).
Multiplayer snowdrift games with reward mechanism and asymmetric factors
The pairwise and multiplayer games considered above do not take into account any reward mechanisms. Such mechanisms, however, have been widely observed in natural mutualistic systems41. In addition, previous models may be oversimplified when accounting for these naturally occurring interactions, implying that cooperative individuals interact symmetrically. We argue, instead, that the interactions between cooperative individuals may more often be asymmetric33,38,42,43,44. To address these limitations, we need a new payoff setup. Another element should also be considered: discrimination between cooperative individuals and defectors is often not possible in many commonly studied mutualisms45,46.
For these reasons, we use a collective reward mechanism for a multiplayer snowdrift game in a single species, as proposed by Ji et al. (2010)47. In their model, the authors allowed cooperative individuals to manifest the fruit of their joint effort earlier on by receiving an additional reward  . This term gives an estimate of the size of the reward as a function of the number of cooperative individuals k47. The parameter w represents the intensity of the reward. This collective reward usually originates from an external pool of resources (as, e.g., in human societies48), or it might take the form of synergistic effects in some biological systems (where the benefits will increase with the increasing number of cooperative individuals)49,50. By definition, a collective reward is imposed on all players either because there is no way to detect the behaviour of individual partners (or its effects) or because the differences between cooperative and non-cooperative individuals are too small to be detected (as in the legume–rhizobium mutualism51). Under these assumptions, we can obtain the payoffs values for a cooperative individual and a defector of species i as:
. This term gives an estimate of the size of the reward as a function of the number of cooperative individuals k47. The parameter w represents the intensity of the reward. This collective reward usually originates from an external pool of resources (as, e.g., in human societies48), or it might take the form of synergistic effects in some biological systems (where the benefits will increase with the increasing number of cooperative individuals)49,50. By definition, a collective reward is imposed on all players either because there is no way to detect the behaviour of individual partners (or its effects) or because the differences between cooperative and non-cooperative individuals are too small to be detected (as in the legume–rhizobium mutualism51). Under these assumptions, we can obtain the payoffs values for a cooperative individual and a defector of species i as:

where the parameters bi, ci, Mi and wi are different for species 1 and 2.
Local dynamics of mutualism
In our model, we study cooperative behaviour in an infinite, well-mixed population. It is also our intent to compute the fractions of cooperative/non-cooperative individuals in the population. The cooperation frequencies of the players of species 1 and species 2 are x(t) and y(t), respectively. The fitness functions of a cooperative individual of species 1 and species 2 are  and
and  , respectively. Based on the interactions occurring between the species, the fitness
, respectively. Based on the interactions occurring between the species, the fitness  depends on the frequency y of cooperative players of species 2,
depends on the frequency y of cooperative players of species 2,  . Similarly, the fitness
. Similarly, the fitness  depends on the frequency x of cooperative players of species 1,
depends on the frequency x of cooperative players of species 1,  . By randomly sampling the groups39,52, we obtained the following average fitness of a cooperative individual and a defector of species 1 and 2:
. By randomly sampling the groups39,52, we obtained the following average fitness of a cooperative individual and a defector of species 1 and 2:


and


Thus, the average payoffs for a player of species 1 and 2 are


The replicator dynamics assume that the per capita growth rate in the population is determined by the difference between the payoff for a particular strategy and the average payoff  53,54,55. Thus, the evolutionary times of x(t) and y(t) are governed by
53,54,55. Thus, the evolutionary times of x(t) and y(t) are governed by

where rx and ry are the evolutionary rates of the two species.
We analysed the dynamics of this game using nonlinear dynamic theory56 and simulations (see the Methods section for more details). Two locally stable equilibrium points (C1, D2) and (D1, C2) arise in our model if the reward wi satisfies wi/bi < djci/bi (with i, j = 1,2 and i ≠ j). The pair of equilibrium points (x,y) in each cell corresponds to the frequency of cooperation of species 1 and 2, respectively. In addition, the equilibrium points (C1, D2) and (D1, C2) are denoted by E2(1,0) and E3(0,1). Thus, the equilibrium points (C1, D2) and (D1, C2) occur where the players of one species are all cooperating and the players of the other species are all defecting. It is important to note that these two stable points have their own basins of attraction (obtaining these basins of attraction has proven extremely useful for analysis of such behaviours25,57,58). As we show in Fig. 2, the ‘grey region’ and the ‘green region’ are the basins of attraction for (C1, D2) and (D1, C2), respectively. In effect, the solution trajectories converge to the point (C1, D2) if the initial strategy frequencies of each species fall within the ‘grey region’, whereas they converge to the point (D1, C2) if the initial strategy frequencies fall within the ‘green region’ (see Fig. 2).
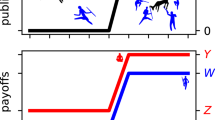
The shift between the Red Queen and the Red King effect, accounting for reward mechanisms.
The black solid circles are locally stable strategies (ESSs) and the empty circles are unstable strategies (non-ESSs). The red solid circles denote inner equilibrium points that are unstable. For equal evolutionary rates, rx = ry, the basins of attraction of the two equilibriums (C1, D2) and (D1, C2) are of equal size ((a), (b) and (c)), whereas the size of these two basins is unequal when the evolutionary rates between two species are asymmetric ((d), (e) and (f)). The colours illustrate the regions leading to the equilibria favourable to species 1 (green region leading to (D1, C2)) and species 2 (grey region leading to (C1, D2)). For a multiplayer game without a reward mechanism (with i = 1,2 and di = 19, wi = 0), the basin of attraction favourable to faster-evolving species grows substantially. However, the internal equilibrium points shift with an increase in the collective reward (with i = 1,2 and di = 19, wi = 5), as in (e). As a result, the Red King effect eventually appears with increasing intensity of the reward, as in (f). This causes a switch from the Red Queen effect (d) to Red King effect (f). The evolutionary rates are rx = 1/8 and ry = 1 in (d), (e), (f). The other parameters are fixed at bi = 2, ci = 1 and Mi = 1.
We propose a method to calculate the benefits to the players of the two species when the stability of mutualisms can be maintained. We begin by assuming that the threshold is Mi = 1 (with i = 1,2) and that the number of players is d1 = d2 for species 1 and 2. The size of the ‘grey region’ and the ‘green region’ is defined as S1 and S2, respectively (0 < S1, S2 < 1, S1 + S2 = 1). The players of cooperative games will eventually adopt an ESS of (C1, D2) with probability S1 and an ESS of (D1, C2) with probability S2. The fitness of the players of species 1 and 2 are thus denoted by B1 = S1·(b1 − c1) + S2·b1 and B2 = S1·b2 + S2·(b2 − c2), respectively. As a result, species 1 will obtain a larger share of returns than species 2 when B1 > B2 and species 2 will obtain a larger share of returns than species 1 when B1 < B2. In addition, the two species obtain equal benefits when B1 = B2 (for more details, see the Supplementary Information section). This implies that, in mutualisms, the division of the benefits (surplus) depends on the size of the basins, Si; on the benefits, bi; and on the costs, ci (with i = 1,2). Using economics terminology, mutualistic benefits can be named as a ‘surplus’ generated by the mutualism20.
When the benefit biand the cost ciof the two species are the same, we return to the methods used in previous studies25,57. Under these conditions, the allocations of mutualistic benefits appear to rely on the size of the respective basins of attraction. In other words, species 1 will reap larger benefits than species 2 when the basin of attraction of (D1, C2) is larger than (C1, D2), whereas species 2 will reap larger benefits than species 1 when the basin of attraction of (C1, D2) is larger than (D1, C2). Intuitively, the size of the basins might reflect the behaviours/strategies of the individuals involved (e.g., the resilience or the lifetime of the state). These behaviours should result from having to adapt to a changing environment over evolutionary time. For each individual in species 1 and 2, the size of the basins of attraction reflects the probability of defection. Individuals with a higher probability of defection will reap larger benefits. In addition, for each species, the size of the basins of attraction reflects the proportion of defectors. The higher the proportion of defectors, the greater the benefit for that species.
Simulations and Discussion
The allocation of mutualistic benefits under asymmetric evolutionary rates
Reward effect
In this section, we assume that the benefit bi, the cost ci, the number of players di and the reward wi of the two species are the same. If the evolutionary rates are unequal (i.e., species 1 with rate rx = ry/8), the basins of attraction of (C1, D2) and (D1, C2) become unequal in size. In other words, the allocation of the resulting benefits is unequal between the two species (Fig. 2d, 2e and 2f). If the game is run without any reward mechanism (with wi = 0), the basin of attraction (C1, D2) is larger than the basin of attraction (D1, C2). This implies that the faster-evolving species will receive a larger share of the benefits (Fig. 2d). This is in line with what is predicted by the Red Queen effect24. However, this effect can shift to the Red King effect when we include the reward variable in the multiplayer game. Specifically, the size of the basin of attraction of (D1, C2) increases substantially as the reward intensity wi increases (Fig. 2e). As a result, the slower-evolving species obtains a larger share of the benefits (Fig. 2f). This means that the initial Red Queen effect shifts to the Red King effect when the magnitude of the reward is over a certain threshold value (Fig. 3c). However, this reward mechanism does not allow the Red King effect to shift to the Red Queen effect (Fig. 3a and 3b). Finally, we find that the size of the reward can accentuate the Red King effect (Fig. 3b and 3c).
The effects of a reward wi and the game size N on the internal equilibrium x*.
We assume the numbers of players between species to be equal, i.e., d1 = d2 = d. Thus, the game size for each species is defined by N and N = d + 1. (a) Given a relatively low reward intensity (i.e., w = 0.8), the internal equilibrium x* is above 0.5 in small groups (e.g., N = 2 or N = 3). (b) For pairwise games, the equilibrium is always above 0.5 for any reward intensity. (c) When the size of the mutualistic group is large (i.e., N = 8), the internal equilibrium can shift from a small value (below 0.5) to a large value (above 0.5) with a rise in the collective reward. The other parameters are fixed at bi = 2, ci = 1 and Mi = 1.
Next, we explore the process resulting from the shift between the Red Queen effect and the Red King effect. From the analyses above, we predict which species would be favoured. As explained, this depends on the relative sizes of the two basins of attraction (C1, D2) and (D1, C2), i.e., S1 and S2. Theoretically, it is difficult to obtain accurate values for S1 and S2. Fortunately, when the evolutionary game is symmetric, we can use values of x and y to measure the size of S1 and S2 (in this case, x = y; further details of this method are reported by Bergstrom and Lachmann (2003)25). Specifically, the replicator solutions of the two species create quadrants in the state space (0 ≤ x, y ≤ 1) (Fig. 2). When the internal equilibrium is x = y = 0.5, the bottom-left and the top-right quadrants are of equal size. As a result of this symmetric geometry, the basins of attraction (C1, D2) and (D1, C2) become the same, i.e., S1 = S2. If the equilibrium is less than x = 0.5, the bottom-left quadrant is smaller than the top-right quadrant, i.e., S1 > S2 (Fig. 2d). As a result, the faster-evolving species would be favoured, as depicted by the Red Queen effect (Fig. 3c). Conversely, if the equilibrium is greater than x = 0.5, the bottom-left quadrant is larger than the top-right quadrant, i.e., S1 < S2 (Fig. 2f). Thus, the evolutionary process will favour the slower-evolving species, as described by the Red King effect25 (Fig. 3c). Interestingly, in a multiplayer game with fixed bi, ci and a fixed number of players, di, the equilibrium x exceeds 0.5 with increasing rewards (Fig. 3c). Thus, the Red Queen effect can shift to the Red King effect and vice versa, depending on the intensity of the rewards. Finally, note that this method is not valid when the evolutionary game is asymmetric (e.g., with asymmetric payoffs or asymmetries in the number of players) because the above geometry becomes asymmetric (with x ≠ y, see Fig. S9 in the electronic Supplementary Material). In this case, we use simulations to estimate the size of S1 and S2.
Asymmetric players
Surprisingly, only recently there has been some focus on the effect of asymmetry in the number of interacting partners (i.e. d1 ≠ d2)33,57. We know that this phenomenon is ubiquitous in nature. Most literature on mutualisms assumes that a single host interacts with and controls the fate of, multiple partners. In the fig and fig wasps mutualism, for example, a single fig is attended by multiple fig wasps. From the perspective of each wasp, this is a pairwise game, but from the perspective of the fig, this is a multiplayer game. However, for symbioses between plants and arbuscular mycorrhizal fungi, plant species are typically colonised by multiple fungal species59 and fungal individuals can simultaneously interact with multiple host plants60 or species61. For one-to-many interactions, when a symbiont evolves much faster than its host–which is often the case–the host can dominate the co-evolutionary process by allowing the Red King effect to appear (see Fig. 4a or Fig. S9a). By contrast, the symbiont becomes dominant in the co-evolutionary race when we consider many-to-many interactions (e.g., the interaction between plants and arbuscular mycorrhizal fungi) (see Fig. 4a or Fig. S9b). This is consistent with the more often cited Red Queen effect. Thus, we conclude that asymmetry in the number of players can produce different effects (i.e., the Red Queen versus Red King). This result is consistent with those of Gokhale and Traulsen (2012).
The influence of asymmetric players or rewards on the allocation of mutualistic benefits.
(1) First, we consider unequal evolutionary rates between the two mutualistic species (rx = 1/8, ry = 1). (a) For a fixed number of players of species 2 (d2 = 8), the difference between S1 and S2 depends on the number of players of species 1 (d1), where S1 and S2 represent the size of the basins of attraction of the equilibrium (C1, D2) and (D1, C2), respectively. For one-to-many interactions between the two species, S2 is larger than S1. Conversely, S1 is larger than S2 when the interactions between species are many-to-many (e.g., d1 = 4). (b) Similarly, by adjusting the intensity of reward for species 2 (w2), the Red King effect (i.e., S2 > S1) can also shift into the Red Queen effect (i.e., S1 > S2) and vice versa (the reward intensity on species 1 is fixed at w1 = 1). (2) For equal evolutionary rates between two species (rx = ry = 1), each player will receive equal mutualistic benefits when the number of players of the two species are symmetric (c) (e.g., di = 8 with i = 1,2). When the numbers of the players of the two species are asymmetric (d1 ≠ 8), each player will receive unequal mutualistic benefits. Similar results can be obtained for the rewards (as in (d)). We also assume that d2 = 8 in (c) and w1 = 1 in (d). The other parameters are fixed at bi = 2, ci = 1 and Mi = 1, w1 = w2 = 0 in (a) and (c) and d1 = d2 = 4 in (b) and (d).
Asymmetric payoffs
In mutualistic interactions, the interacting players can obtain different rewards at different times (i.e.w1 ≠ w2). The Red King effect can shift to the Red Queen effect by adjusting reward asymmetry. Similarly, the Red Queen effect might be reversed by adjusting reward asymmetry (Fig. 4b or Fig. S9c and 9d). In fact, the payoff matrices become asymmetric because of the different rewards wi, benefits bi and costs ci for the two species.
In summary, the reward mechanism and the asymmetry of interactions (e.g., asymmetry in payoffs or the number of players) might determine the ultimate allocation of mutualistic benefits (the Red Queen effect or the Red King effect). These results might provide an explanation for why, in some mutualisms, the faster-evolving species are dominant (e.g., in the endophytic fungi and grasses mutualism, the fungi appear to reduce the host's tendency to reproduce sexually; sex seems to be the critical element4). In other mutualisms, the slower-evolving species are dominant (e.g., in the invertebrate-algal and lichen mutualisms62,63 or the host-endosymbiont mutualisms64). Therefore, opposite outcomes may result from differences in the payoffs, in the number of players and in the reward mechanism across species.
The allocation of mutualistic benefits under equal evolutionary rates
Given symmetrically interacting species with equal evolutionary rates, the allocation of benefits between the two species will be equal (Fig. 4c or Fig. S9e). In the case of asymmetry, however, the species with fewer participants will receive relatively more benefits (Fig. 4c or Fig. S9f). In addition, the asymmetric rewards imply that benefits are allocated unevenly. If the rewards are equal, the benefits should also be equal (Fig. 4d or Fig. S9g). Instead, the species that gets fewer rewards will have a stronger tendency to freeload and will receive greater benefits without paying the related costs (Fig. 4d or Fig. S9h). In addition, we can assume that the asymmetry in initial benefits or costs causes an unequal allocation of resulting benefits.
Note that these specific results are suitable for the allocation of benefits within a single species constituted by two types of players with equal evolutionary rates. In specific instances, the resulting benefits arising from the cooperative behaviour may be allocated to the participants according to a set of rules (e.g., a social hierarchy). This often happens in social animal groups, e.g., in lions and wolves when displaying cooperative hunting behaviour.
Complex Cooperation
Different social dilemmas can arise within the context of multiplayer games. When the thresholds Mi are adjusted, we incur a scenario of complex cooperation. In adjusting the thresholds Mibetween two species, not only do we observe a bistability between all cooperative individuals and all defectors (Fig. 5a) but we also find that the cooperative individuals and the defectors can coexist through a rock-paper-scissors dynamic (as shown by the “white region” with closed orbits in Fig. 5b). Furthermore, by accounting for an asymmetry in the thresholds (i.e., M1 ≠ M2), the cooperative system follows the boxed pigs game, in which only one side chooses to cooperate, but the other side inevitably defects (Fig. 5c).
Complex cooperative behaviours in the snowdrift game with a reward or a general threshold.
(a) If the thresholds for the two species are M1 = 1 and M2 = 1, a bistability is observed between all cooperative individuals and all defectors. (b) When M1 = 1, M2 = 3, we observe the “white regions” with closed orbits in the interior. The initial conditions falling within the “grey region” will converge to the equilibrium (C1, D2) and those falling within the “green region” will converge to the equilibrium (D1, C2). (c) When M1 = 1, M2 = 6, all initial conditions lead to (D1, C2). At this point, only one side chooses to cooperate while the other side chooses to defect. (d) In the special case of Mi = di+1 and wi = 0 with i = 1,2, the equilibrium point (C1, C2) (the ‘pink region’) is an ESS. In this case, full cooperation among players becomes possible. The other parameters are fixed at di = 4, bi = 2, ci = 1,wi = 0 with i = 1,2 and rx = ry = 1.
Finally, yet importantly, a special case is represented by those human societies showing a division of labour. For a functioning cooperation, it is required that each player cooperates to complete the task (Mi = di + 1). In such situations, we witness an extreme outcome: a stable state of full cooperation arises (i.e., E4(1,1) is an ESS – the ‘pink region’ in Fig. 5d).
Conclusion
To analyse how benefits are shared between two mutualistic species, we established a multiplayer snowdrift game model that incorporated a reward mechanism. This model demonstrates that the Red Queen effect can shift to the Red King effect and vice versa by adjusting the intensity of the rewards. When the rewards are small, the Red Queen effect is observed; when the rewards exceed a certain threshold, the Red Queen effect transforms into the Red King effect. To make the model more realistic, we also included asymmetric payoffs and asymmetries in the number of interacting partners. By changing the degree of asymmetry of the reward or the number of interacting partners, we again found that the Red Queen effect can shift to the Red King effect. Even in situations where the evolutionary rates are equal between the two species, the asymmetric factors (e.g., asymmetry in the reward wi, in the benefits bi, in the costs ci or in the different number of interacting individuals belonging to the two species di) can create an inequality in the allocation of the resulting benefits between the partners.
Moreover, some complex cooperative strategies might be observed by manipulating the thresholds Mi. First, for more general thresholds (i.e., with Mi > 1 and i = 1,2), the cooperative individuals and the defectors seem to coexist with oscillating frequencies. Second, when there is an asymmetry in the thresholds (i.e., M1 ≠ M2), the system falls into the dilemma of the boxed pigs game, in which only one side chooses to cooperate and the other side chooses to defect. Third, in the special case of all participants cooperating, a benefit is generated such that a state of full cooperation becomes stable in the population.
Methods
The dynamics of an evolutionary snowdrift game with a reward mechanism
The evolutionary times of x(t) and y(t) of the two species are governed by the following replicator dynamic equations25,57

From equation (9), we can obtain four boundary equilibrium points denoted as E1(0,0), E2(1,0), E3(0,1) and E4(1,1). In addition, using simulations, we can obtain the inner equilibrium points and denote them as: E(xi,yi) where i = 1,2. The elements of vector (x,y) are the frequencies of the cooperative individuals of species 1 and 2, respectively. It is, however, difficult to obtain the analytical expressions of xiand yi for large group sizes N because the inner equilibrium points should satisfy the following equations with N powers

The stability of the nonlinear system can be determined from the analysis of linearisation56. Thus, to analyse the evolutionary stability of the replicator dynamics (9) with N + 1 powers, we should first obtain the linearisation of the dynamics at every equilibrium point. The linearisation of the replicator dynamics (9) at an equilibrium point  becomes
becomes

where



and

To simplify this analysis, we assume that the benefits bi, the costs ci, the rewards wi and the thresholds Mi(with i = 1,2) of the two species are the same. By analysing the property of the matrices' eigenvalues, produced by the linearisation of the replicator dynamics (11) at the equilibrium points, we find that:
Scenario (1) 1 ≤ Mi < di + 1 with i = 1,2. The equilibrium points E1(0,0), E(x1,y1) and E(x2,y2) are sources (unstable); the equilibrium points E2(1,0) and E3(0,1) are locally stable, if wi/bi < djci/bi.with i,j = 1,2 and i ≠ j. In addition, the equilibrium point E4(1,1) is a sink (stable), if wi/bi > djci/bi;
Scenario (2) Mi = di + 1 with i = 1,2. The equilibrium points E1(0,0), E2(1,0) and E3(0,1) are sources (unstable) and the equilibrium point E4(1,1) is a sink (stable).
References
Edwards, D. P., Hassall, M., Sutherland, W. J. & Douglas, W. Y. Selection for protection in an ant–plant mutualism: host sanctions, host modularity and the principal–agent game. Proc. R. Soc. B. 273, 595–602 (2006).
Neish, A. S. The gut microflora and intestinal epithelial cells: a continuing dialogue. Microb. Infect. 4, 309–317 (2002).
Nechaev, S. & Severinov, K. The elusive object of desire–interactions of bacteriophages and their hosts. Curr. Opin. Microbiol. 11, 186–193 (2008).
Herre, E. A., Knowlton, N., Mueller, U. G. & Rehner, S. A. The evolution of mutualisms: exploring the paths between conflict and cooperation. Trends Ecol. Evol. 14, 49–53 (1999).
Holland, J. N., DeAngelis, D. L. & Schultz, S. T. Evolutionary stability of mutualism: interspecific population regulation as an evolutionarily stable strategy. Proc. R. Soc. B. 271, 1807–1814 (2004).
Trivers, R. L. The evolution of reciprocal altruism. Q. Rev. Biol. 46, 35–57 (1971).
Bronstein, J. L. Our current understanding of mutualism. Q. Rev. Biol. 69, 31–51 (1994).
Anderson, R. & May, R. Coevolution of hosts and parasites. Parasitology 85, 411–426 (1982).
West, S. A., Pen, I. & Griffin, A. S. Cooperation and competition between relatives. Science 296, 72–75 (2002).
Kiers, E. T., Rousseau, R. A., West, S. A. & Denison, R. F. Host sanctions and the legume–rhizobium mutualism. Nature 425, 78–81 (2003).
Frank, S. A. Mutual policing and repression of competition in the evolution of cooperative groups. Nature 377, 520–522 (1995).
Wang, R.-W., Sun, B.-F. & Zheng, Q. Diffusive coevolution and mutualism maintenance mechanisms in a fig-fig wasp system. Ecology 91, 1308–1316 (2010).
Wang, R.-W., Dunn, D. W. & Sun, B. F. Discriminative host sanctions in a fig-wasp mutualism. Ecology 95, 1384–1393 (2014).
Dunn, D. W. et al. A role for parasites in stabilising the fig-pollinator mutualism. PLoS Biol. 6, e59 (2008).
Wang, B., Geng, X. Z., Ma, L. B., Cook, J. M. & Wang, R. W. A trophic cascade induced by predatory ants in a fig-fig wasp mutualism. J. Anim. Ecol. 83, 1149–1157 (2014).
Hamilton, W. D. The genetical evolution of social behaviour. II. J. Theor. Biol. 7, 17–52 (1964).
Bshary, R. & Schäffer, D. Choosy reef fish select cleaner fish that provide high-quality service. Anim. Behav. 63, 557–564 (2002).
Grutter, A. S. Cleaner fish really do clean. Nature 398, 672–673 (1999).
Bshary, R. & Grutter, A. S. Asymmetric cheating opportunities and partner control in a cleaner fish mutualism. Anim. Behav. 63, 547–555 (2002).
Bergstrom, C. T. & Lachmann, M. Evolutionary Rates and the Division of Surpluses in Mutualisms. Genetic and Cultural Evolution of Cooperation 223 (MIT Press, Cambridge, 2003).
Pierce, N. E. Peeling the onion: Symbioses between ants and blue butterflies. Model Systems in Behavioral Ecology, ed. LA Dugatkin 41–56 (Princeton University Press, Princeton, 2001).
Vázquez, D. P. & Aizen, M. A. Asymmetric specialization: a pervasive feature of plant-pollinator interactions. Ecology 85, 1251–1257 (2004).
Dillon, R. & Dillon, V. The gut bacteria of insects: nonpathogenic interactions. Annu. Rev. Entomol. 49, 71–92 (2004).
Van Valen, L. A new evolutionary law. Evol. theory 1, 1–30 (1973).
Bergstrom, C. T. & Lachmann, M. The Red King effect: when the slowest runner wins the coevolutionary race. Proc. Natl. Acad. Sci.USA 100, 593–598 (2003).
Damore, J. A. & Gore, J. A slowly evolving host moves first in symbiotic interactions. Evolution 65, 2391–2398 (2011).
Hilbe, C., Nowak, M. A. & Sigmund, K. Evolution of extortion in Iterated Prisoner's Dilemma games. Proc. Natl. Acad. Sci.USA 110, 6913–6918 (2013).
Wang, Z., Xu, Z.-J. & Zhang, L.-Z. Punishment in optional public goods games. Chin. Phys. B 19, 0201 (2010).
Wang, Z., Szolnoki, A. & Perc, M. Rewarding evolutionary fitness with links between populations promotes cooperation. J. Theor. Biol. 349, 50–56 (2014).
Sigmund, K., Hauert, C. & Nowak, M. A. Reward and punishment. Proc. Natl. Acad. Sci.USA 98, 10757–10762 (2001).
Szolnoki, A. & Perc, M. Reward and cooperation in the spatial public goods game. EPL (Europhysics Letters) 92, 38003 (2010).
Wang, R., Yang, Y. & Wiggins, N. L. Asymmetric or diffusive co-evolution generates meta-populations in fig-fig wasp mutualisms. Sci. China Life Sci. 57, 1–7 (2014).
Wang, R.-W., Sun, B.-F., Zheng, Q., Shi, L. & Zhu, L. Asymmetric interaction and indeterminate fitness correlation between cooperative partners in the fig–fig wasp mutualism. J. R. Soc. Interface 8, 1487–1496 (2011).
Pellmyr, O. & Huth, C. J. Evolutionary stability of mutualism between yuccas and yucca moths. Nature 372, 257–260 (1994).
Pellmyr, O. & LeebensMack, J. Reversal of mutualism as a mechanism for adaptive radiation in yucca moths. Am. Nat. 156, S62–S76 (2000).
Wang, R.-W. et al. Interference competition and high temperatures reduce the virulence of fig wasps and stabilize a fig-wasp mutualism. PLoS One 4, e7802 (2009).
Hofbauer, J. Evolutionary dynamics for bimatrix games: A Hamiltonian system? J. Math. Biol. 34, 675–688 (1996).
Maynard Smith, J. Evolution and the Theory of Games (Cambridge university press, Cambridge, 1982).
Souza, M. O., Pacheco, J. M. & Santos, F. C. Evolution of cooperation under N-person snowdrift games. J. Theor. Biol. 260, 581–588 (2009).
Axen, A. H. & Pierce, N. E. Aggregation as a cost-reducing strategy for lycaenid larvae. Behav. Ecol. 9, 109–115 (1998).
Kiers, E. T. et al. Reciprocal rewards stabilize cooperation in the mycorrhizal symbiosis. Science 333, 880–882 (2011).
Grafen, A. The logic of divisively asymmetric contests: respect for ownership and the desperado effect. Anim. Behav. 35, 462–467 (1987).
Nikiforakis, N., Normann, H.-T. & Wallace, B. Asymmetric enforcement of cooperation in a social dilemma. South. Econ. J. 76, 638–659 (2010).
He, J., Wang, R., Christopher, X. J., Li, Y. & Li, C. Cooperation in an asymmetric volunteer's dilemma game with relatedness. Chin. Sci. Bull. 57, 1972–1981 (2012).
Archetti, M. & Scheuring, I. Trading public goods stabilizes interspecific mutualism. J. Theor. Biol. 318, 58–67 (2013).
Jandér, C. K., Herre, E. A. & Simms, E. L. Precision of host sanctions in the fig tree–fig wasp mutualism: consequences for uncooperative symbionts. Ecol. Lett. 15, 1362–1369 (2012).
Ji, M., Xu, C., Zheng, D.-F. & Hui, P. Enhanced cooperation and harmonious population in an evolutionary N-person snowdrift game. Physica A 389, 1071–1076 (2010).
Chen, X., Gross, T. & Dieckmann, U. Shared rewarding overcomes defection traps in generalized volunteer's dilemmas. J. Theor. Biol. 335, 13–21 (2013).
Kun, Á., Boza, G. & Scheuring, I. Asynchronous snowdrift game with synergistic effect as a model of cooperation. Behav. Ecol. 17, 633–641 (2006).
Hauert, C., Michor, F., Nowak, M. A. & Doebeli, M. Synergy and discounting of cooperation in social dilemmas. J. Theor. Biol. 239, 195–202 (2006).
Kiers, E. T., Rousseau, R. A. & Denison, R. F. Measured sanctions: legume hosts detect quantitative variation in rhizobium cooperation and punish accordingly. Evol. Ecol. Res. 8, 1077–1086 (2006).
Pacheco, J. M., Santos, F. C., Souza, M. O. & Skyrms, B. Evolutionary dynamics of collective action in N-person stag hunt dilemmas. Proc. R. Soc. B. 276, 315–321 (2009).
Taylor, P. D. & Jonker, L. B. Evolutionary stable strategies and game dynamics. Math. Biosci. 40, 145–156 (1978).
Hauert, C., De Monte, S., Hofbauer, J. & Sigmund, K. Replicator dynamics for optional public good games. J. Theor. Biol. 218, 187–194 (2002).
Hofbauer, J. & Sigmund, K. Evolutionary games and population dynamics (Cambridge University Press, Cambridge, 1998).
Hirsch, M. W., Smale, S. & Devaney, R. L. Differential equations, dynamical systems and an introduction to chaos (Academic Press, New York, 2004).
Gokhale, C. S. & Traulsen, A. Mutualism and evolutionary multiplayer games: revisiting the Red King. Proc. R. Soc. B. 279, 4611–4616 (2012).
Shigaki, K., Wang, Z., Tanimoto, J. & Fukuda, E. Effect of Initial Fraction of Cooperators on Cooperative Behavior in Evolutionary Prisoner's Dilemma Game. PloS one 8, e76942 (2013).
Vandenkoornhuyse, P. et al. Active root-inhabiting microbes identified by rapid incorporation of plant-derived carbon into RNA. Proc. Natl. Acad. Sci.USA 104, 16970–16975 (2007).
Mikkelsen, B. L., Rosendahl, S. & Jakobsen, I. Underground resource allocation between individual networks of mycorrhizal fungi. New Phytol. 180, 890–898 (2008).
Selosse, M.-A., Richard, F., He, X. & Simard, S. W. Mycorrhizal networks: des liaisons dangereuses? Trends Ecol. Evol. 21, 621–628 (2006).
Smith, D. C. & Douglas, A. E. The biology of symbiosis (Edward Arnold (Publishers) Ltd., 1987).
Doebeli, M. & Knowlton, N. The evolution of interspecific mutualisms. Proc. Natl. Acad. Sci.USA 95, 8676–8680 (1998).
Frean, M. R. & Abraham, E. R. Adaptation and enslavement in endosymbiont-host associations. Phys. Rev. E 69, 051913 (2004).
Acknowledgements
We thank Riccardo Pansini, Arne Traulsen, Jun-Zhou He, Ya-Qiang Wang, Chao-Qian Li, Qi-Long Liu for their discussion and comments during the preparation of this manuscript. We also thank the three anonymous reviewers and Jin Yoshimura for constructive comments that enabled us to improve the manuscript. This research was supported by the National Natural Science Foundation of China (31370408, 31170408, 31270433, 71161020), the National Science Fund for Distinguished Young Scholars (31325005), NSFC-Yunnan United fund (U1302267), the Postgraduate Science Foundation of the Yunnan University (Grant No. ynuy201366), the West Light Foundation of the Chinese Academy of Sciences and the Special Fund for the Excellent Youth of the Chinese Academy of Sciences (KSCX2-EW-Q-9).
Author information
Authors and Affiliations
Contributions
Conceived and designed the model: R.W.W. and Y.T.L. Performed the research: L.G. Analysed the model: L.G. Wrote the paper: R.W.W. and L.G. All authors revised the manuscript and approved the final version.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Electrical Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Gao, L., Li, YT. & Wang, RW. The shift between the Red Queen and the Red King effects in mutualisms. Sci Rep 5, 8237 (2015). https://doi.org/10.1038/srep08237
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep08237
This article is cited by
-
Eco-evolutionary Logic of Mutualisms
Dynamic Games and Applications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.